果蝇鸣声信号结构分析与时频子波建模

吕苗荣，刘 绪

（常州大学 石油工程学院，江苏 常州 213164）

各种动物为了实现与外界环境的有效联系，受到外界刺激或出于自身生理需要均会发出不同的鸣叫声，对动物发声行为的研究是动物行为生态学研究的重要方面。昆虫的发声机制主要有敲击外界物体发声、摩擦发声、靠翅膀或胸壁振动发声、膜振动发声和空气振动发声等[1]。果蝇通过振翅所产生的鸣声可实现种群内个体间的召唤、求偶、攻击和报警等方面信息的传递。1962 年Shorey 首次对果蝇的振翅声进行了分析[2]，Tauber 和Eberl 实现了果蝇发声和鸣声信号的采集[3]，Webb 等分析了加勒比海果蝇鸣声的振翅频率、声强和谐波成分，实现了不同日龄雌雄果蝇的识别[4]。Sivinki 等研究了雄性果蝇的召唤、求偶和交尾声的环境及行为[5]。Mizarch 等将地中海果蝇的研究成果应用于果蝇的诱集捕杀[6]。

人们一般从时域和频谱两个方面开展果蝇鸣声信号研究[7]，在信号建模方面文献[8]实现了短时窗信号功率谱密度的参数和非参数建模。随着信号处理技术的进步，声谱图、美尔倒谱系数、小波变换等方法也被应用于果蝇振翅波形特性和果蝇振翅声信号识别的研究。文献[9]研究表明，果蝇胸部在飞行期间产生的声音由两种主要的振动模式组成：机翼拍频和骨骼振动。文献[10]分析了瓜蝇鱼雄性交配鸣声产生的机制。文献[11]证实了寄生蝇能在飞行时进行声学定向。

信号处理的目的就是从果蝇鸣声信号中提取得到果蝇行为、目标、动作以及与环境相互作用等各种特征信息[12-13]。笔者将工程信号处理方法应用到果蝇鸣声的研究中，对果蝇振翅进行了基本描述，采用模式滤波法进行果蝇信号时频子波的分解、分类和鸣声信号的分离与建模处理。

1 信号的基元分段处理

1.1 信号基本操作单元的确定

按照文献[14]的观点，信号的基本操作单元就是指在具有周期特征的信号中，对所研究的周期现象截取一个个具有完整周期特征的基本信号段，将其简称为基元或基元信号。基元信号所对应的样本点数量称为基元长度，用M表示；相应的时间段长度，即基元周期也称为基元时长，用tM表示。tM与采样率之间存在如下关系式：

式中：FSP为果蝇鸣声信号采样率，Hz。

例如，图1(a)是一个从某生物声信号库中下载的果蝇鸣声信号。如果截取图1(a)中指定间隔A的信号段进行时域放大显示，可以获得图1(b)。而图1(c)是将图1(b)中指定的B信号段进行时域放大后显示的结果。如果将图1(c)的分段信号按照标定的1、2、3…等进行分段处理，切分获得的信号段就是果蝇鸣声信号的基元信号。音频测试表明，图1(c)所示的信号是果蝇振翅一次所对应的小段信号。如果按照图1(c)所示的分段形式，并采用分段相关性系数最高为标准进行精确定位，可以获得如图2(a)所示的基元信号汇总结果，图2(b)是对应的基元频谱图。

果蝇鸣声基元的切分并不是绝对的。从图1(c)或图3 可以看出，信号内部还存在着果蝇飞行期间完成一个完整的飞行动作所对应的另一类周期特征信号。

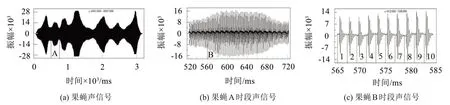
图1 果蝇声信号及频谱

图2 果蝇声信号基元分段信号及频谱

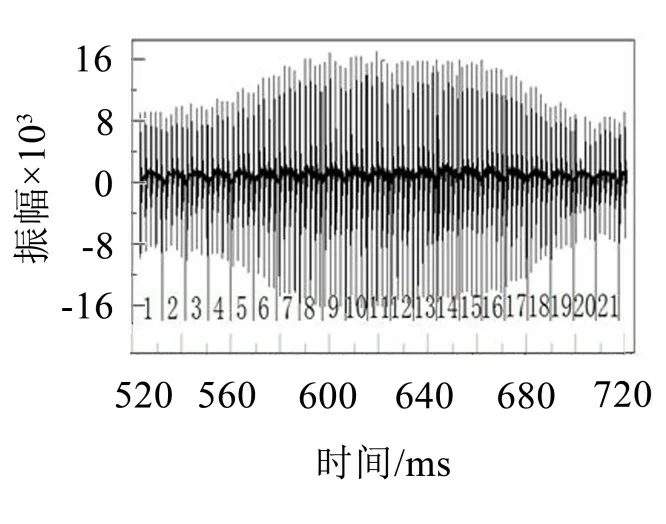
图3 果蝇声信号基元分段的另一种划分形式

1.2 果蝇基元信号的多普勒特征

对比图2(a)和图2(b)可以看出，果蝇飞行期间，由于飞近和飞离声传感器而导致的多普勒频移现象主要体现在基元时长的变化上，对基元波形没有影响，基元信号频谱也几乎保持不变。

显然，人们一方面可以通过研究一个具体的基元信号，来建立物化系统各种变量之间内在的关联与规律性。另一方面，也可以通过研究一个个前后相继的基元信号参数序列的变化特征，来掌握整个系统的变化趋势，实现对现实世界的有效检测与控制。因此，研究基元信号是了解“微观”特征与掌控“宏观”趋势的钥匙，也是连接“微观”与“宏观”之间的桥梁。图4 就是图1(a)果蝇鸣声信号的基元振幅和基元长度变化曲线图。这些基元参数曲线能够很好地揭示果蝇鸣声信号内部变化的过程与特征。

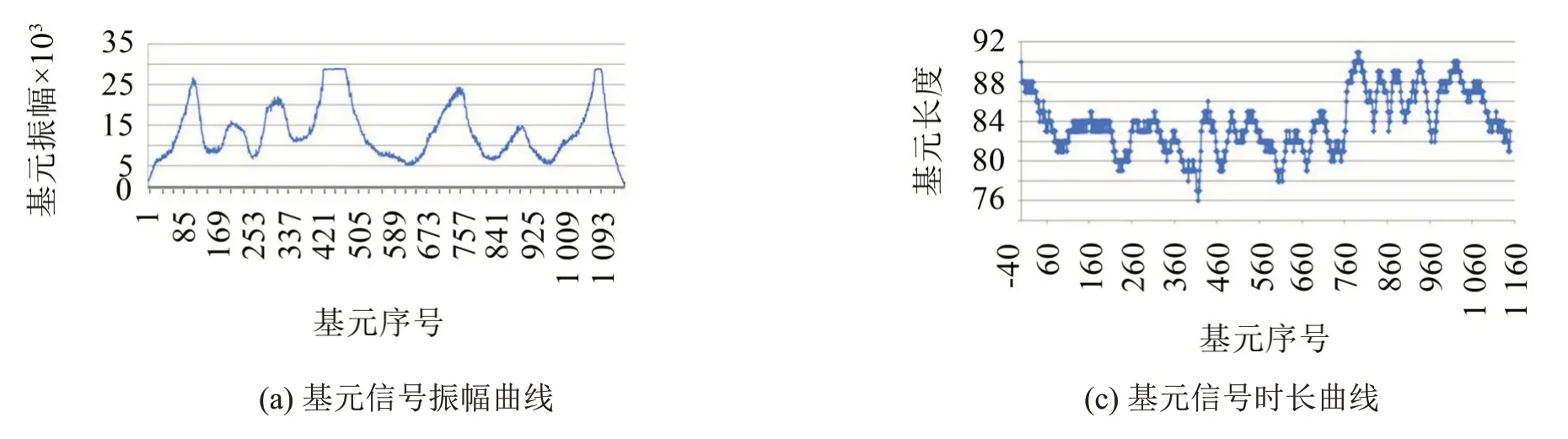
图4 果蝇声信号基元参数曲线

1.3 果蝇鸣声基元信号分类

将果蝇鸣声基元信号进行时长补齐处理，使所有的基元信号保持长度一致，而后做30次基元信号循环，将新形成的信号再进行信号频谱归类处理。研究表明，即使是相关性系数下限为0.975，归类结果也只有5类。在总共1 151个基元信号中，序号范围在1～1 147的为一类，序号为1 148、1 149、1 150、1 151的各自为一类。

如果按照波形信号相关性系数的高低进行分类，按信号互相关性系数高低进行归类处理，在保持相关性系数下限为0.975的情况下，可以获得图5所示的17个分类结果。

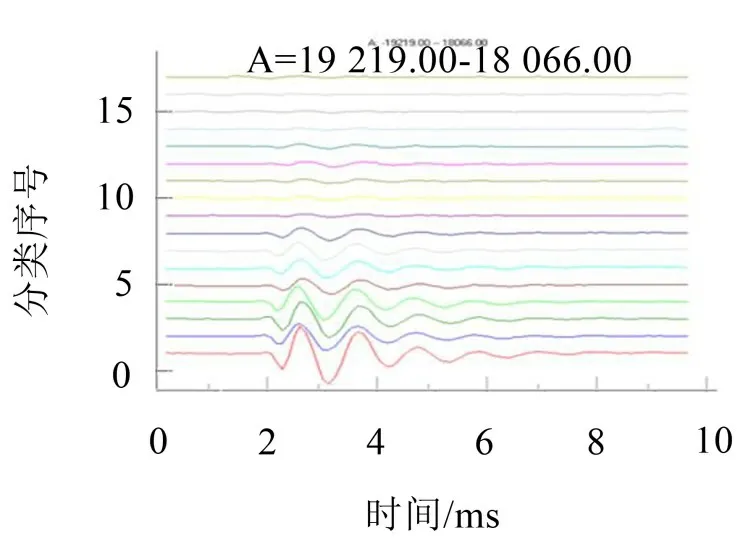
图5 果蝇基元信号典型分类曲线

如果将整个果蝇鸣声信号中的所有基元信号用某个基元信号以振幅大小按比例进行替换，并比较替换前后的音频效果。测试表明，除了1 148～1 151的独立分类基元信号形成的鸣声声效发生明显变异，对其他基元信号进行替换后形成的鸣声声效与原信号比较几乎没有变化。这一测试结果表明果蝇鸣声基元信号结构具有良好的稳定性。

2 信号的模式滤波法处理

2.1 果蝇鸣声信号的模式滤波分解

2.1.1 果蝇鸣声信号时频子波分类

按照文献[14]介绍的按照模式滤波法进行分解处理，并对分解后获得的时频子波进行归类处理，在匹配下限为0.975时，可以将所有子波归并为图6所示的498类，其中f代表频率，α代表衰减系数。定义每个基元中振幅最大的时频子波为基元主子波。以基元主子波时间为参考点，对第i个基元的每个子波做以下转换：

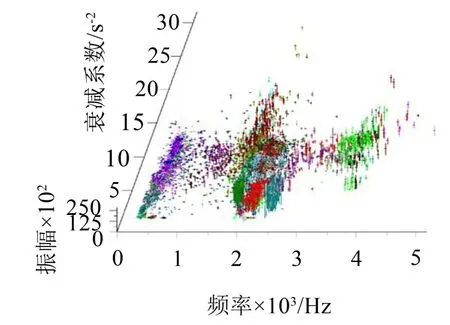
图6 果蝇信号时频子波在“f-α-A”空间分布

式中：tbij是第i个基元内第j个子波经过转换后的时间值，称为第j个子波的基元子波时间，s；t0ij是第i个基元内第j个子波在果蝇信号内的时间值，t0ij=β0ij/β1ij；t0im是第i个基元主子波在信号内的时间值（i=1，2，…，N，N是基元总数量）。

将果蝇时频子波分布在“tb-jBOU”平面内，其中jBOU是基元序号，时频子波就会在tb时间轴的某些点上集中聚集。因此，在498类时频子波的基础上，再按照tb时间轴进行进一步的分类处理，最终获得3 134个分类结果。

对所有分类重构信号进行音频测试与归类处理，可以获得表1 所示的13 项二次归类时频子波分类结果。这13 类鸣声振动子类信号又可进一步归并成为以下4 个大类：翅膀振动摩擦、果蝇鸣声、胸骨振动和果蝇整体冲击振动。

表1 果蝇时频子波归类结果

2.1.2 并发时频子波的提取与处理

并发时频子波的概念有两个：一个是时间并发时频子波，指的是在分解后的子波中存在着许多t0ij数值相同的时频子波，笔者定义这些子波为时间并发子波；另一个是结构并发时频子波，指的是在不同的基元信号中，同时出现的在相同时间点tbij上同类型、基元结构相似的时频子波。由于并不是所有波形都能够用一个时频子波进行合理的逼近与替代。时间并发子波的作用就是对基元并发主子波的波形起到修饰和补偿的作用，以便更好地逼近（或适应）实际的信号。在时间并发时频子波中，振幅最大的时频子波被称为是并发主子波，其它子波称为并发非主子波。

图7(a)所示是果蝇信号并发非主子波在“β1-α-A”空间的分布。从图上可以看出，这些子波按照频率可以分成高低两类。图7(b)是这两类子波的重构信号。测试表明，由高频并发非主子波重构的信号主要是由果蝇飞行时翅膀之间的接触摩擦振动引起；而低频并发非主子波是由果蝇飞行期间胸骨撞击和身体的强烈冲击发出的声音。从图7(b)也可以看出，翅膀接触摩擦振动往往与飞行方向的转折紧密相关，飞行平稳、方向稳定时接触摩擦很小、甚至没有。而低频撞击和冲击振动似乎与果蝇飞行期间的发动、制动、平稳滑行等状态相对应的肢体动作密切相关，笔者也称这些子波为动作子波。

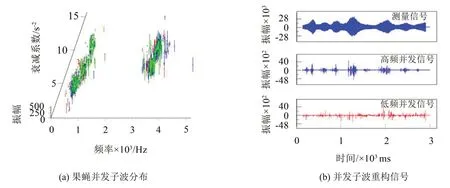
图7 果蝇并发子波及重构信号

2.1.3 果蝇基元信号主子波

分析表明，在基元主子波中不存在时间并发子波。但在所有的1 151 个基元中，有2 个或2 个以上与主子波类型相同的情况，参见表2，余下基元主子波数量只有1 个的类型有1 345、1 346、1 350、2 464、2 471、2 484，共6个。

在这些分类主子波中，前3 类分别包含735 个、270个和96个主子波，形成了果蝇鸣声信号3个大的子类基元信号。剩余的只有46个（占总数4%）基元主子波。测试表明，表2 中所示的基元主子波重构信号的音效已经与原信号十分接近。

2.1.4 分类子波分布的规律性

分析表明，各种时频子波在参数空间中具有特定的分布规律。例如，表1 中3 次归类子波中2～4类子波在“tb-jBOU”二维空间中的子波分布情况可参见图8(a)。可以看出，深绿色的第3类的胸骨振动位于主子波（即tb=0）之前，蓝色的第2类翅膀摩擦振动紧随主子波之后，而浅绿色的第4 类低频整体冲击子波排在靠后出现。

在表1所示3次归类的第2类果蝇鸣声信号中，2次归类为4的时频子波排在主子波之前，紧随主子波的是2次归类为3的鸣声子波，与翅膀摩擦几乎同时出现的是2 次归类为11 的低频有节律鸣声，具体可参见图8(b)。果蝇飞行期间产生的各种鸣声和果蝇飞行行为与动作紧密相关。

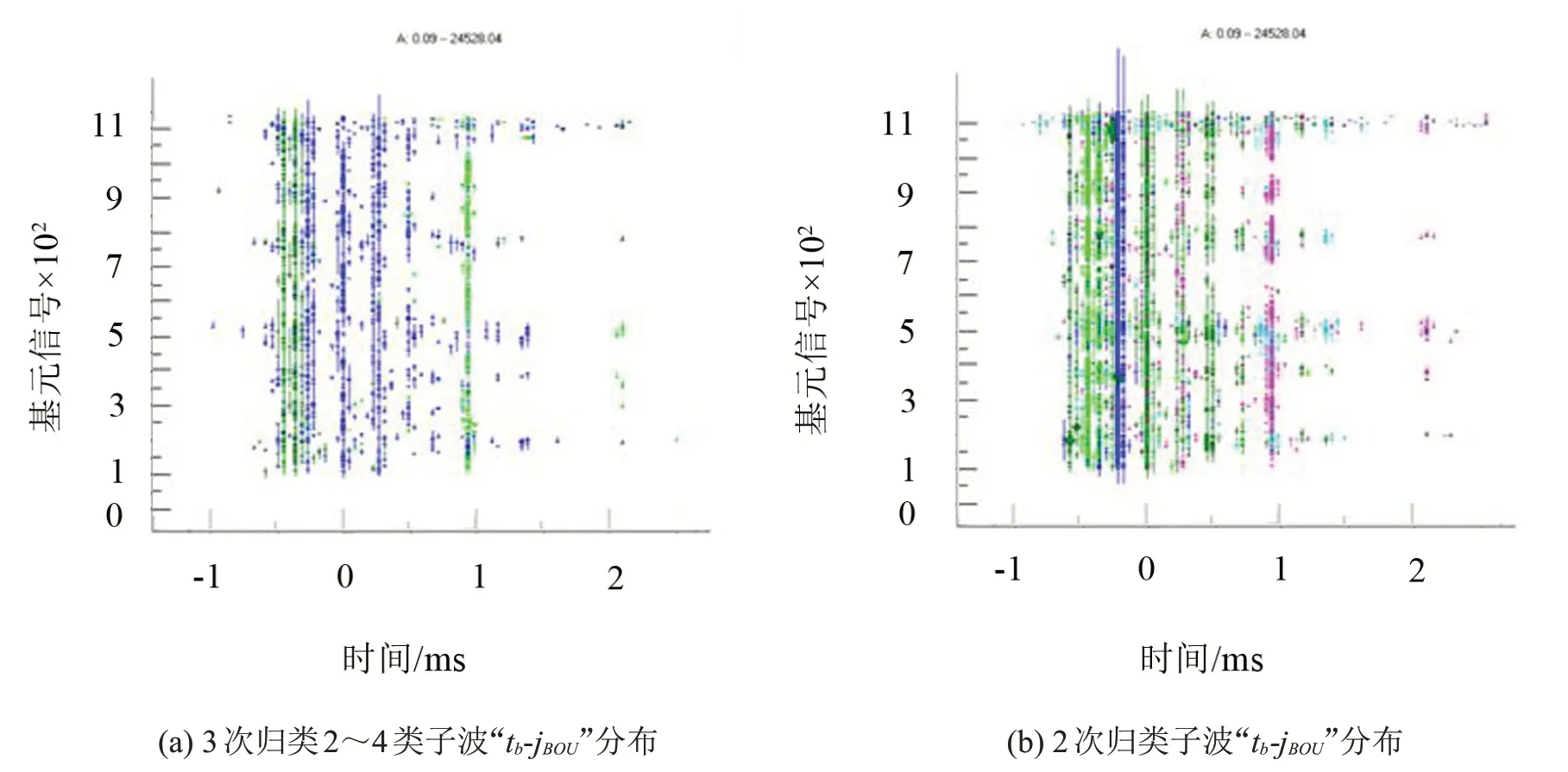
图8 果蝇信号子波在“tb-jBOU”二维平面分布

2.2 果蝇鸣声基元信号结构分析

果蝇鸣声基元信号内部时频子波的排布存在固定的结构形式，表3 所示是以表2 中的主基元为参照，对3 134 类时频子波并发统计汇总后，取子波数量的前7位进行列表获得的结果。所谓基元子波并发统计是指对134类不同类型的时频子波在同一个基元信号中出现次数的统计。

表2 与基元主子波同类的基元数量汇总表

从表3 可以看出，构成果蝇鸣声基元信号的主要类型为基元主子波1、3、12这3类。以主子波第1类为例，与基元主子波并发出现的前11类非主子波在不同的参数空间的分布可参见图9(a)、图9(b)和图9(c)。从图上可以看出，分类序号为1的主子波集中于β0=0 轴周围，对应果蝇飞行的相对平稳状态。对应第3 类和第12 类的主时频子波和前11 类并发非主时频子波在β0上分别在小于零和大于零的范围内分布，对应果蝇的降速飞行和加速飞行状态。

表3 基元子波并发次数部分统计结果

每一类并发非主子波也很好地反映了各种状态之间的转换规律。例如，对应1#主子波并发子波占所有非主子波的百分比几乎都是50%。而其它的3#、12#、85#等类与主子波并发出现的非主子波总和又占50%。因此，与非主子波相关的状态之间转换几乎都发生在1#和其它主子波，以及同类主子波之间。从图9 可以看出，不同主子波和非主子波在参数空间中的分布主要集中在特定的tb点上，非主子波随主子波的变化在“β1-β0-A”空间分布也各具特点，基元信号组成和结构非常稳定。

图9 随第1类主子波并发出现的前11类非主子波在参数空间中的分布

3 果蝇鸣声信号建模

3.1 分类子波振幅参数回归处理

如果将3 134 类时频子波分类结果中的类与类之间的振幅参数，以基元为单位进行子波振幅的散点显示，可发现基元子波振幅参数的变化存在很好的线性对应关系。表4所示就是利用这些数据进行回归处理获得的结果。

3.2 果蝇基元信号主频与基元长度的关系

利用文献[14]介绍的基元延时循环信号的构建方法来处理基元信号，在3 个系列上，基元长度为76、77、78～85、89、86～88 和90 的信号基元长度与基元循环信号主频之间呈线性关系，具体如表5 所示。初步分析表明，序号为1 的回归结果绝大部分位于果蝇飞行的后2/5段内，序号为2的数据散点很少；占3/5的前半段正好与占2/5的后半段相反，序号为2的散点数据占绝大部分，序号为1的散点数据则很少；产生这样的结果与果蝇飞行状态密切相关。利用这3个系列的散点数据，可以通过回归得到表5所示的结果。

表5 果蝇信号基元长度与基元循环信号主频回归结果

3.3 果蝇基元信号的时频子波表征

根据上面的分析，可以得出基于时频子波果蝇基元信号的表达式为：

式中：yBOU(t)是时域基元信号波形表达式；A0是果蝇声源的振幅，mPa；fi是第i系列时频子波的频率，Hz；ai、bi是表4所示的第i系列时频子波与第1系列时频子波线性回归系数；β0i是第i系列时频子波的初始相位，rad；M是子波系列数量。

表4 基元子波振幅参数线性回归统计结果

4 结语

通过开展果蝇鸣声信号的基元分段处理和模式滤波分析，获得了果蝇鸣声信号基元的特征波形、信号时频子波的分类与组成、基元信号的基本结构，以及果蝇运动参数在时域微观与宏观上的变化规律，可以获得以下几点结论：

（1）果蝇鸣声信号具有很强的周期变化特征，包含有低频整体冲击振动信号和高频振翅飞鸣信号这两个系列的基元信号，分别对应果蝇振翅一次或飞行期间果蝇做一个完整的飞行动作所对应的小段信号；

（2）果蝇飞行期间，由于距离的变化导致的多普勒频移现象主要体现在基元长度的变化上，基元波形和单一基元频谱几乎保持不变；

（3）对果蝇鸣声信号进行模式滤波法处理，分解所得的时频子波可以分为13个细类和4个大类，4大类鸣声信号分别是翅膀振动摩擦、果蝇鸣声、胸骨振动和果蝇整体冲击振动声信号；

（4）以基元主子波为参照，可以获得基元信号时频子波的基本结构特征。果蝇时频子波可以按照主子波在参数空间中的位置分为3 大类，分别对应平稳运动、加速运动和降速运动。

（5）分类时频子波之间的参数存在一定的依存关系。基元结构并发类时频子波的振幅可以用线性关系式进行描述处理。

（6）通过分析建立了基于时频子波的果蝇基元信号数学模型。

由于系列子波的出现与否同果蝇的飞行状态有关，因此，如要形成一个完整的果蝇飞行信号精细化动态数学模型，还需要建立果蝇基元信号状态转移模型。限于篇幅，更详细的讨论可参见笔者后续的介绍。