基于时间反转声学理论的超声相控阵超分辨率成像方法*

樊程广，余孙全，赵 勇，杨 磊

(国防科技大学 空天科学学院， 湖南 长沙 410073)

超声相控阵是一种新型的超声传感器，包含多个阵元，每一个阵元可以发射和接收声波信号。通过计算机技术控制阵列中各个阵元激励脉冲的时间延迟，可以灵活控制合成波阵面的偏转和聚焦，达到扫描成像的目的。因此，将超声相控阵置于被测对象表面的固定检测位置，可以对被测对象内部的某一个区域进行扫描成像，其已被广泛应用于工业无损检测领域[1-3]。利用超声相控阵对被测对象进行检测时，首先，采用全矩阵采集(Full Matrix Capture, FMC)方法在线获取超声阵列数据。FMC方法利用阵列的每一对阵元组合获取超声回波信号，因此数据中包含了与被测对象相关的最大量信息，同时数据可以被不同的成像方法处理，避免了重复采集，降低了实验成本[4-5]；其次，利用不同成像方法对超声阵列数据进行离线处理，得到超声图像。成像方法是时域信号转换为图像的“桥梁”，相同的数据被不同的成像方法处理，得到不同质量的超声图像；最后，提取超声图像特征，评估被测对象内部状况。分辨率是重要的评价指标，表征成像方法区分被测对象包含相邻点目标的能力。

瑞利准则定义了常规成像方法的分辨率极限，若被测对象中相邻点目标的距离小于分辨率极限时，根据超声图像无法区分相邻点目标。其中，分辨率极限与超声波工作波长相关，为了提高成像分辨率，需要使用更高频率的超声波；但是，超声波的工作频率越高，其在介质中传播时的衰减越厉害，影响探测深度[6]。如何在保持超声波工作频率不变且不影响系统探测深度的前提下，提高成像分辨率，即为本文研究的超分辨率成像。

Fink等基于声学波动方程的时间反转不变性，提出了时间反转声学(Time Reversal Acoustics, TRA)理论，并将其应用于无损检测领域[7]。Lev-Ari等在时间反转声学理论的基础上，结合多信号分类(MUltiple SIgnal Classification, MUSIC)法，提出了单阵元脉冲回波工作模式下的时间反转多信号分类(Time Reversal-MUltiple SIgnal Classification, TR-MUSIC)法[8]，并随后扩展至双阵元传输工作模式[9]。利用TR-MUSIC法对介质中相邻点目标进行成像，在理论模型中考虑声波在不同目标之间的多次散射(Multiple Scattering, MS)，仿真结果验证了TR-MUSIC对相邻点目标的超分辨率特性[10-11]。Simonetti等通过理论分析指出，声波在不同目标之间的MS包含了目标的次波长信息，因此，MS是实现超分辨率成像的关键因素，但是，de Rosny等对该结论提出了异议，故而MS在超分辨率成像中的具体作用有待进一步研究[12-13]。由于TR-MUSIC具备超分辨率特性，其已经在医学成像领域得到了研究，并被应用于乳腺癌细胞的成像和定位[14-17]。此外，由于医学成像领域和无损检测领域存在差异[18]，需要进一步研究TR-MUSIC的超分辨率特性及其在无损检测领域的应用。

1 超声相控阵检测原理

利用超声相控阵对被测对象进行检测，其原理如图1所示。在笛卡尔坐标系中，一维线性阵列的中心位置为坐标原点o，其所包含的N个阵元沿x轴方向均匀分布，阵元宽度为a。激励阵元发出的超声波在x-z平面传播，由接收阵元接收，x-z平面中包含理想点散射体。

图1 超声相控阵检测原理图Fig.1 Detection schematic diagram of ultrasonic phased array

对于阵列的任意一组阵元组合Rtx-Rrx，超声回波信号的频域表达如式(1)所示[19]。

Htx,rx(ω)=F(ω)Dtx(θtx,ω)G(Rtx,rs,ω)

fsG(rs,Rrx,ω)Drx(θrx,ω)

(1)

式中，F(ω)是阵元输出信号频谱，fs为理想点散射体的散射系数。

Dtx(θtx,ω)和Drx(θrx,ω)是阵元在固体介质中的远场指向性函数，其定义分别如式(2)～(3)所示。

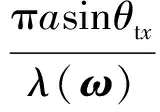
(2)

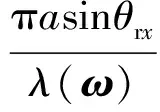
(3)

其中，λ(ω)为超声波波长，cL和cS分别为超声纵波和超声横波在介质中的传播速度，θtx和θrx的定义如图1所示。F0函数的定义如式(4)所示。

F0(ξ)=[2ξ2-(cL/cS)2]2-

4ξ2(ξ2-1)1/2[ξ2-(cL/cS)2]1/2

(4)

G(Rtx,rs,ω)和G(rs,Rrx,ω)为介质的格林函数，定义如式(5)所示。

(5)

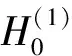
利用FMC方法获取超声阵列数据，如图2所示。由于FMC方法利用阵列的任意一对阵元组合获取超声回波信号，因此，由其获取的超声阵列数据包含N2个信号。

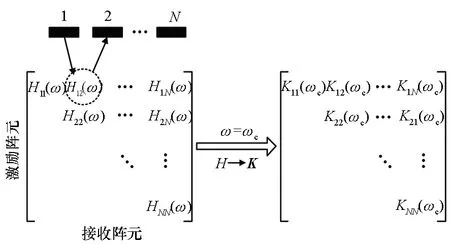
图2 超声阵列数据和阵列响应矩阵Fig.2 Ultrasonic array data and array response matrix

2 时间反转多信号分类法数学定义

2.1 阵列响应矩阵

阵列响应矩阵描述了超声相控阵检测系统中不同阵元之间的脉冲响应。对于一个工作在回波模式的N元阵列，其任意阵元均可用于激励和接收声波信号，依次激励阵列中的阵元，由其引起的声波信号同时被阵列的N个阵元接收，即可得到阵列响应矩阵K[20]。在实际应用过程中，通常通过超声阵列数据构建阵列响应矩阵K，其计算过程如图2所示。给定工作频率，通常选择阵列中心频率ωc，提取其对应的H(ωc)值，作为矩阵K(ωc)的元素，构建阵列响应矩阵，其为N×N复矩阵。

2.2 奇异值分解和子空间划分

TR-MUSIC法通过对阵列响应矩阵进行奇异值分解(Singular Value Decomposition, SVD)实现成像目的[11, 21]。

K(ω)的奇异值分解方程如式(6)所示。

K(ω)=U(ω)Σ(ω)VH(ω)

(6)

式中，U(ω)和V(ω)由奇异向量组成，Σ(ω)由奇异值组成，上标H表示复矩阵的共轭转置。

根据奇异值分布特征，将奇异向量(μi和νi)划分为信号子空间(US(ω),VS(ω))和噪声子空间(UN(ω),VN(ω))，如式(7)～(8)所示。

U(ω)=[US(ω)|UN(ω)]

=[μ1(ω),…,μm(ω),|μm+1(ω),…,μN(ω)]

(7)

V(ω)=[VS(ω)|VN(ω)]

=[ν1(ω),…,νm(ω),|νm+1(ω),…,νN(ω)]

(8)

其中，m为信号子空间的维度。

2.3 TR-MUSIC成像函数

给定成像区域，对于成像区域中的任意像素点r，定义方向向量g(r,ω)，如式(9)所示。

g(r,ω)=[G(R1,r,ω),…,G(RN,r,ω)]T

(9)

式中，Rl(l=1～N)表示阵元位置，上标T表示复矩阵的转置。

在阵列中心频率点ωc处，根据方向向量和信号子空间，定义TR-MUSIC成像函数如式(10)所示。

(10)

式中，‖·‖表示范数。

2.4 点扩散函数

点扩散函数(Point Spread Function, PSF)描述超声成像系统对理想点散射体的响应[19]。给定阵列和理想点散射体，利用FMC方法获取超声阵列数据，通过成像方法得到理想点散射体的超声图像，提取图像特征用于评价不同成像方法。

数值仿真参数设置为：一维线性阵列包含64个均匀分布的阵元，所有阵元可以激励和接收超声波，超声波在介质中的传播速度为6 300 m/s，成像区域为20 mm×20 mm，在成像区域中有一个理想点散射体，其位置坐标为(x=0,z=20 mm)，其散射系数定义为1。利用FMC方法获取超声阵列数据，由于线性阵列包含64个阵元，因此，超声阵列数据共包含4 096个时域信号。利用平面B扫描方法和TR-MUSIC方法处理超声阵列数据，得到理想点散射体的二维和三维超声图像，如图3所示。平面B扫描是常用的基于延迟和叠加原理(Delay And Sum, DAS)的波束形成技术，由于其操作简单，对噪声具备鲁棒性，已经被广泛用于工业无损检测领域[4]。对于TR-MUSIC方法，利用其对介质中的理想点散射体成像时，在不考虑噪声的前提下，其信号子空间的维度与理想点散射体的数目一致[22]，因此，在仿真过程中，信号子空间的维度选择为1。

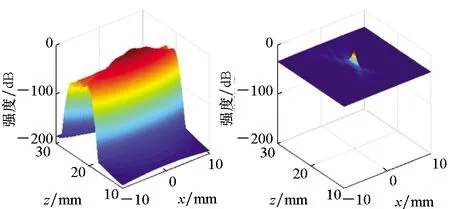
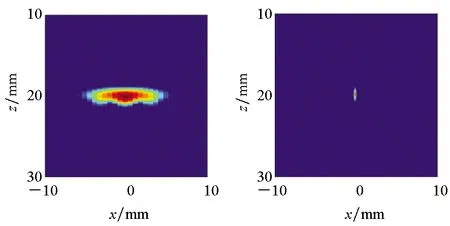
图3 点扩散函数Fig.3 Point spread function

由图3可知，基于平面B扫描和TR-MUSIC图像均可定位理想点散射体的位置。相较于平面B扫描方法，TR-MUSIC方法的成像结果中的理想点散射体的图像区域明显变小，说明其成像分辨率得到提高。

3 实验验证

3.1 实验系统

实验系统原理图如图4所示，主要包括阵列控制器、线性阵列传感器以及测试对象。阵列控制器的一端与PC机相连，一端与线性阵列相连，阵列通过耦合剂放置在测试对象表面。PC机发出指令，通过阵列控制器控制阵列传感器中各个阵元的激励和接收。

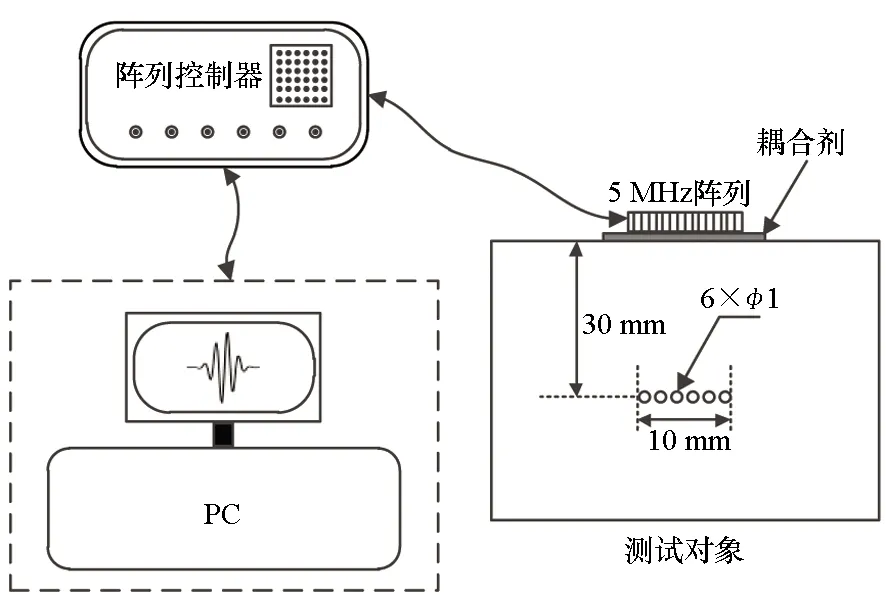
图4 实验系统原理Fig.4 Principle of experimental system

图5 实验设备Fig.5 Experimental equipment

实验设备实物图如图5所示，其中阵列控制器选择英国Peak NDT公司的MicroPulse 5PA，其参数见表1，它包括128个独立通道，用于进行数据传输，其中每一个通道可以进行16位的数据采集。线性阵列传感器选择法国Imasonic公司的5 MHz、64元线性阵列，其参数见表2。

表1 阵列控制器参数

表2 线性阵列参数

测试对象选择不锈钢试块，在其内部加工6个直径为1 mm的贯通孔。超声波在不锈钢试块中的传播速度为6 150 m/s，在阵列传感器中心频率5 MHz处，其对应的波长为1.23 mm，大于贯通孔直径1 mm，因此，这6个贯通孔可视为点散射体。

3.2 实验结果分析

首先，利用FMC方法获取超声阵列数据。由于超声波在固体介质中传播时，存在超声纵波、横波等，因此，对于超声阵列数据中的每一个时域信号，需要从中提取与缺陷相关的散射信号，选择在时域加窗函数的方法进行提取，部分原始信号和提取的散射信号如图6所示。

其次，对预处理后的时域信号进行时域-频域转换，在阵列传感器的中心频率点处，构建阵列响应矩阵。由于阵列包含64个阵元，因此，阵列响应矩阵为64×64的复矩阵。

再次，对阵列响应矩阵进行奇异值分解，在阵列中心频率点处，得到64个奇异值，其分布曲线如图7所示。在64个奇异值中，前11个奇异值大于剩下的奇异值，因此，信号子空间的维度设定为11。信号子空间维度会影响超声成像结果质量。信号子空间维度过小，基于超声图像无法定位所有目标；信号子空间维度过大，超声成像结果中存在伪目标，无法准确评估被测对象内部状况。

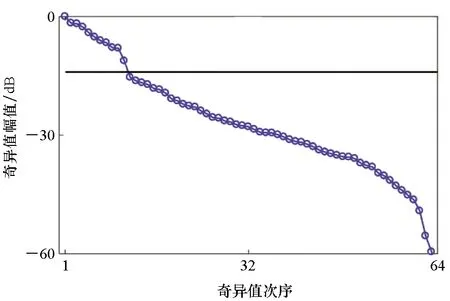
图7 奇异值分布曲线Fig.7 Distribution of singular values

最后，设定成像区域20 mm×20 mm，对于其中的任意像素点，定义方向向量，基于信号子空间得到TR-MUSIC图像，如图8所示。为了进行比较，图8给出了基于相同超声阵列数据得到的常规平面B扫描图像。

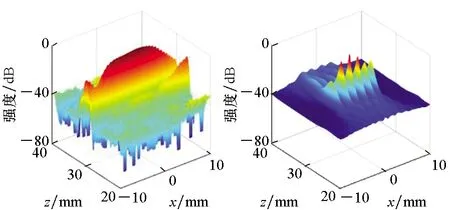
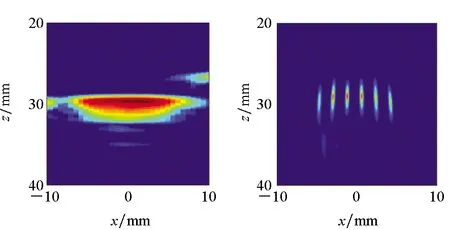
图8 实验结果Fig.8 Experimental results

由图8可知，基于平面B扫描图像，无法区分不锈钢试块包含的6个相邻贯通孔，基于TR-MUSIC图像，则可以区分这6个相邻贯通孔，并且对其进行准确定位。实验结果验证了TR-MUSIC方法的超分辨率特性。

4 结论

本文研究基于时间反转声学理论的超分辨率成像方法，用于解决常规超声成像分辨率受到超声波波长限制的问题。详细阐述了超声相控阵检测原理；给出了TR-MUSIC法的数学定义，通过数值仿真分析了其点扩散函数；搭建了实验系统，通过实验验证了其超分辨率特性。实验在不锈钢试块上完成，在试块的内部加工6个可视为点散射体、直径为1 mm的贯通孔。实验结果表明，相比较常规的平面B扫描方法，TR-MUSIC方法可以克服瑞利准则，实现超分辨率成像，提高超声图像质量。