遥测参数数据载荷状态判别集成学习方法*

李 虎，郭国航，胡 钛，杨甲森，董振兴

(1. 中国科学院国家空间科学中心 空间科学卫星运控部， 北京 100190; 2.中国科学院大学， 北京 100049; 3. 中国科学院国家空间科学中心 复杂航天系统电子信息技术重点实验室， 北京 100190)

有效载荷是实现航天任务目标的关键组成部分，直接决定任务的成败。遥测数据是地面运管人员判断有效载荷在轨运行状态最重要的依据[1]。传统地面运管系统主要提供基于门限的常规参数级判读，状态判别则需要专家系统支持。航天任务中有效载荷功能各异，设备参数更多，工作方式更复杂，地面运管系统面临载荷设备遥测参数维度高、数据量大、类别不平衡和无法直观判别设备运行状况等新问题。如何进行高效在轨任务监视、载荷任务调度和参数优化设计等，决定了有效载荷运行的科学性和有效性。

基于遥测数据的航天器统计学习方法，可构建不完全依赖于航天器领域知识[2]，由数据驱动的分析模型和方法。当前国内外学者主要的研究方向是面向在轨航天器故障异常发现[3]和卫星平台参数判读，其中海量遥测参数数据降维和特征选取方面主要采用主成分分析(Principal Component Analysis, PCA)[4]方法，即主要采用基于时间序列[5]的相似性度量和回归预测。文献[6]采用主成分分析理论对高维遥测数据进行降维处理，从高维数据集中提取低维特征组合，设计了航天器故障定位检测算法。文献[7]针对卫星姿态故障类型和故障源难以辨识问题，利用主成分分析测量卫星姿态与传感器之间遥测数据特征值比例变化进行故障判断。文献[8]对运载火箭飞行过程积累的历史数据进行分析，提出一种基于历史数据统计特性的遥测缓变参数自动判读方法。文献[9]在“天绘一号”01星任务中提出一种基于数据库软件的遥测数据快速处理方法和卫星重点参数监视判读方法。文献[10]以极限学习机(Extreme Learning Machines, ELM)预测模型为基础，采用集成学习方法对目标参数在时间维度上的变化趋势进行预测和判读。文献[11]采用仿真模型对大型充液卫星的在轨模式进行识别。上述文献基于遥测参数处理分析应用研究，围绕航天器通用分系统故障和卫星平台参数判读积累了丰富的经验，所采用的主成分分析方法属于“压缩式”降维，主要存在以下问题：①缺乏对有效载荷设备状态判别的研究；②所使用的方法、模型对类别不平衡支持不够友好；③对面向主题的高维数据特征选择缺少可解释性；④分析结果无法提供影响因素的丰富信息。一方面，航天器任务分析对解释性有较高要求，分析方法和结果要能按遥测量进行准确的人工一致性验证。另一方面，载荷仪器的高精密性、复杂性和任务安排的高灵活性，要求地面运管工作尽可能全面地覆盖载荷领域知识。这些对地面运管系统和运管人员提出了挑战。因此，本文提出一种将信息增益特征筛选方法和集成学习相结合，实现应用于航天任务运行工作的遥测参数数据载荷设备状态判别方法，以支持面向载荷设备任务模式的遥测参数数据自适应学习和判别。

1 问题模型

1.1 遥测参数数据和载荷状态张量表示

定义1TM={tmj|j=1,2,…,n}为载荷遥测参数集合，tmj为第j维遥测参数。

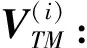
(1)

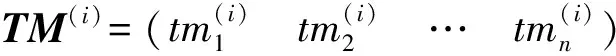
定义3P={pk|k=1,2,…,l}为任务有效载荷设备集合，pk表示第k载荷设备状态。

定义4载荷设备状态向量U(i)：

(2)

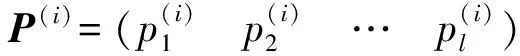
1.2 基于遥测参数数据的载荷单机设备状态判 别问题模型

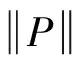
h:ΩTM→ΩP1×ΩP2×…×ΩPl

(3)

给定多标签训练样本集D={(TM(i),P(i))|1≤i≤s}，对于每条样本记录(TM(i),P(i))，TM(i)∈ΩTM为记录的n维特征向量，P(i)∈ΩP1×ΩP2×…×ΩPl为记录TM(i)对应的标签。则给定样本记录数据集D中学习到多标签分类器为：

h(TM(i))=P(i)

(4)

1.3 标签相关性和遥测参数数据类别不平衡

标签相关性是指多标签问题中，数据集中样本所属的标签类别之间具有的相关性[13]，例如互相独立或互斥。基于遥测参数数据的载荷设备状态判别时，由于航天器任务载荷间的协作关系，航天器任务多载荷单机设备状态对应的多标签之间存在相关性，高维度标签和分类数量会影响学习训练的复杂度和运算量，而借助载荷单机设备间的协作相关性，可实现多标签空间的降维，将问题转化为多分类问题。

类别不平衡是指分类问题中出现有些类别的样本量非常少，呈现出不同类别所对应的样本量分布不均匀。类别不平衡会影响以样本量权重为依据的模型分类准确率。遥测参数数据在载荷工作状态中类别不平衡现象较普遍，航天任务工作模式调度决定了处于特定工作状态的载荷遥测参数样本占比比较低，这些状态的判别不能出现漏判或误判。在遥测数据的载荷设备状态判别领域，需要能够准确判别各类状态，载荷设备状态拟合能覆盖到不均匀的样本集。

2 基于遥测参数数据的载荷单机设备状态 判别

设计基于遥测参数原始数据进行载荷单机设备状态判别，步骤如下：

步骤1：依据定义2和定义4所提遥测参数数据向量和载荷设备状态向量对样本数据建立多标签，按照时标形成问题模型中对应的记录组。

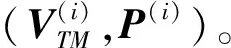
步骤3：根据任务调度时间表对记录组进行采样，分别建立训练集、测试集。

2.1 算法框架

基于问题模型和遥测参数数据分析设计算法框架，见图1。首先，根据航天器分包遥测得到的海量载荷遥测原始数据集和载荷任务状态文件，进行原始数据数值化、合并和解析处理等；然后采用3σ原则一阶数据差分[14]进行野值剔除，并根据遥测数据星上时和载荷状态进行时间对标和分段筛选得到样本特征集；最后基于样本统计的性质、信息增益和任务属性进行特征筛选和多标签特征问题转化。其中，载荷状态数据以可扩展标记语言(eXtensible Markup Language, XML)格式组织。

2.2 算法模型

梯度提升树是集成学习的主要方法之一，其综合了加法模型、回归树模型和梯度提升算法，可更好地拟合训练数据。这种线性组合分类器通过改变样本的权重可以适应类别不平衡问题，并引入bagging和正则化项方法应对样本数据中的噪声。梯度提升决策树(Gradient Boosting Decision Tree，GBDT)基于弱学习器，经多次迭代得到特征切分点构成强分类器，并在迭代的每一步构建沿梯度最陡的方向降低损失的学习器来弥补已有模型的不足，每个弱学习器记录损失函数的梯度残差[15]。梯度提升决策树见图2。

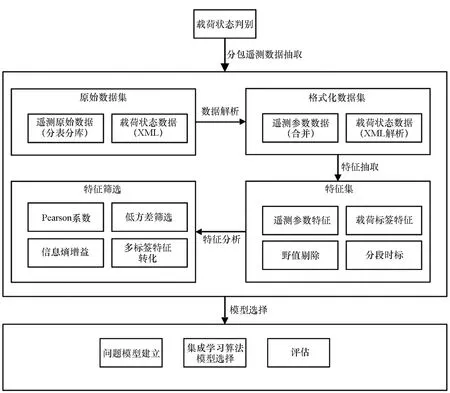
图1 算法框架Fig.1 Algorithm framework

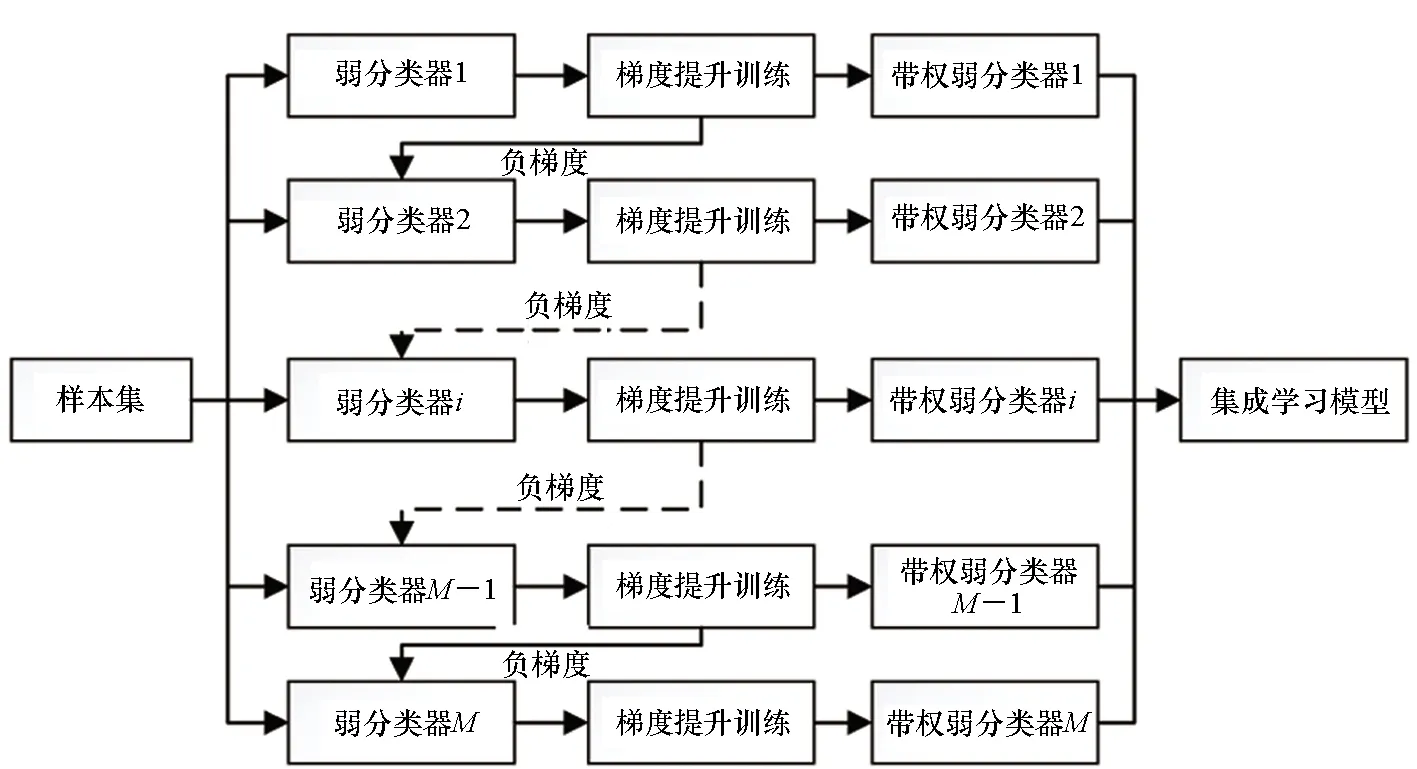
图2 梯度提升决策树Fig.2 Gradient boosting decision tree

文中设计的算法是基于梯度提升的集成学习算法，最终构建遥测参数原始数据与载荷状态的映射关系。将1.2节定义的多标签遥测参数数据集D作为输入，多标签分类器h(·)为输出。梯度提升决策树模型表示为弱分类器的加法模型：

(5)

其中，T(tm;Θm)为弱分类器，Θm为弱分类器的参数，M为弱分类器的个数。

式(5)中第m个弱分类器在第i个样本的梯度残差为：

(6)

其中，L为损失函数。

2.3 特征选择与降维

模型特征降维的可解释性要求为获得的新特征集能与人工归因一致，模型解释的关键在于特征贡献度，因此需要特征选择方法尽可能保留参数信息并不失可解释性。本文根据样本特征集的统计量性质，借助信息增益分析载荷状态样本特征集分布特性，剔除与目标问题相关性低和参数间相关度高的冗余特征，完成特征筛选和降维，保留重点参数特征以提高载荷单机状态判别模型的训练效率和准确度。方法主要包括皮尔逊相关系数[16]、方差和信息熵增益计算等，与主成分分析、互信息方法相比，效率更高并可以保留载荷参数信息。

1)航天器任务皮尔逊相关系数，即

(7)

其中：ρ2(a,b)=1表示两变量相关，ρ2(a,b)=0表示变量不相关；ρ2(a,b)接近1，表示两变量线性关系密切，ρ2(a,b)值越小表示两变量的线性相关越弱。

对遥测数据特征样本集计算两者间的相关系数，若满足|ρ2(a,b)-1|≤ε，则保留其中之一特征。

2)遥测数据的一个特点是有大量的恒定值或缓变值，这些值给分类模型带来运算量，也会干扰模型的准确率，需根据样本方差性质去除该类遥测数据。由于特征方差小表示该特征中多数样本值接近，分类效果不足；特征方差大表示该特征样本值差别较大，因此设计删除低方差的特征。

3)信息增益。熵可表示随机变量的不确定性，根据随机变量的概率分布将熵定义为

(8)

其中，pi是随机变量的概率。熵只依赖于随机变量的分布，与Pi取值无关。

根据随机变量的条件概率可得条件熵

(9)

特征A对训练数据集D的信息增益定义为集合D的经验熵H(D)与特征A给定条件的经验条件熵H(D|A)的差，见式(10)。

g(D,A)=H(D)-H(D|A)

(10)

根据载荷状态标签特征集和遥测参数特征样本特征集，遍历各参数特征对载荷状态标签的信息增益，获得增益排序Rank，选择信息增益大的特征。

通过皮尔逊相关系数、方差和信息增益计算等处理，可尽可能保留遥测参数的原始信息，并实现特征维度的降低，同时兼顾可解释性和模型有效性。

2.4 基于遥测数据的载荷状态判别算法流程

根据1.2节中问题模型和2.2节中算法模型，设计基于遥测数据的载荷状态判别算法如下：

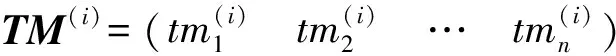
步骤2：计算遥测参数特征集任意二者间的Pearson相关系数，对线性相关度高的特征参数进行处理，保留其中之一特征，得到本步骤筛选后的遥测参数特征集TM′。

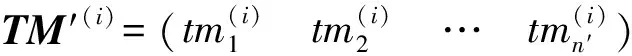
步骤4：使用GBDT算法进行迭代：

1)初始化弱学习器：

(11)

2)m=1,2,…,M，M即弱学习器数目上限，迭代流程如下：

①对样本特征集TM″，计算负梯度残差

(12)

②将残差作为新样本值得到下棵树的数据集{TM″,rmi}，得到新的回归树hm(tm)对应的叶子节点区域Rjm(j=1,2…,J)，J为该回归树的叶子节点数目。

③根据经验风险最小化准则对回归树的叶子区域进行计算最佳拟合

(13)

④更新学习器

(14)

3)得到最终学习器

(15)

3 实验结果与分析

实验验证在Python集成开发环境Pycharm，采用Scikit-learn机器学习库实现算法，以量子科学实验卫星6台载荷的在轨运行数据为样本，对基于遥测参数数据的载荷单机设备状态判别算法进行验证。实验中遥测数据特征集是根据任务分包遥测从遥测原始数据中抽取，6台载荷单机设备的载荷设备状态向量对应5种工作模式组合，将这些模式转化成多标签分类问题。经过实验验证，提取特征维度为p=6，弱分类器个数为150时，可以得到最优的载荷单机状态识别效果。

模型评价指标采用准确率(Acc)和F1-Score。Acc计算正确预测样本占总样本的百分比，代表所有类的整体分类表现；F1-Score通过精确率(Precision)和召回率(Recall)对分类器进行整体评价，高F1-Score意味着分类器对少数类别和多数类别均能识别。对于K个类别：

(16)

(17)

式(16)和式(17)为准确率和F1-Score的计算方法。TPi、TNi、FPi、FNi分别代表样本i识别为样本i，非样本i识别为非样本i，非样本i识别为样本i，样本i识别为非样本i。

实验从三个方面进行：①将遥测原始数据按照2.3节所述方法处理，计算每维数据相对于标签的信息增益(Information Gain, IG)，构建特征样本集，并划分为训练集和测试集；②对比不同特征参数组合下GBDT模型实验性能，选择最优特征参数；③和其他算法进行对比实验，验证所提方法的有效性。

3.1 数据准备

选取量子科学实验卫星2017年至2019年的运行数据来进行算法验证，经过2.4节步骤1和步骤2的预处理后，共获得579维特征，76 699条数据样本。将其中的70%作为训练集，剩余30%作为测试集。本实验的载荷单机状态识别问题，归约为多标签分类问题之后，采用文献[13]中的方法，将多标签分类问题转化为多分类问题来进行求解。转化成多分类问题后的数据分布如图3所示，易见其存在着严重的载荷工作模式类别不平衡，可采用GBDT模型，通过集成多个弱分类模型，能很好地拟合该数据分布。

图3 载荷工作模式数据分布Fig.3 Data distribution of payload mode

3.2 IG-GBDT算法实验结果与分析

载荷单机状态与各组件运行状态息息相关，数据上反映为遥测参数数据与载荷单机状态的相关。因此，采用信息增益作为特征提取的依据。

实现基于IG-GBDT算法的载荷单机状态判别，采用3.1节中数据完成算法训练和测试，需确定模型中两个参数：应用IG算法筛选的特征维度；GBDT模型中弱分类器集成个数。

首先，选用对数损失函数，固定其他参数，改变特征参数维度，构建GBDT分类器，分别计算训练集和测试集数据的损失；之后，选取分类损失最低的特征参数集合作为IG-GBDT模型的特征集。本实验中，随特征维度变化，IG-GBDT模型损失变化如图4所示。当特征参数维度p=6时，模型损失达到最小值，特征维度增加未能明显降低模型损失，确定该模型特征参数维度为6。模型在训练集和测试集中的损失都较小，两者的损失曲线差别不大，显示了该模型具有较低的方差和偏差。

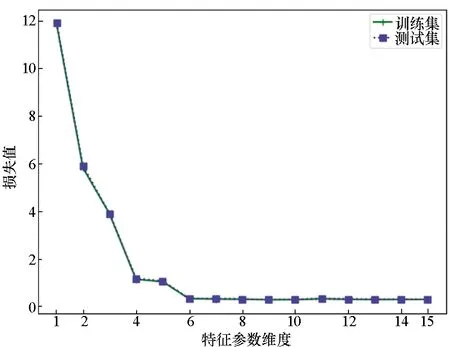
图4 训练集和测试集损失值与特征参数维度的关系Fig.4 Relation between loss of training & testing sets and feature dimension

其次，确定GBDT模型规模，即GBDT模型中弱分类器的集成个数。参照筛选确定的特征参数集，调整模型中弱分类器个数，观察训练集与测试集损失变化，如图5所示。随着弱分类器数量的增加，训练集和测试集的损失值都在下降，起初损失值下降速率很快，当达到一定数目后，损失值变化幅度趋于平缓，继续增加弱分类器会导致计算复杂度的增加。从损失值变化曲线可知，当弱分类器数量达到150时，损失值的变化趋于稳定，考虑到模型计算资源消耗，确定弱分类器个数为150。

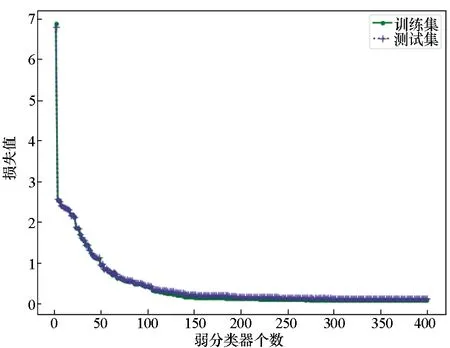
图5 训练集和测试集损失值与弱分类器个数的关系Fig.5 Relation between loss of training & testing sets and number of base classifiers

在确定特征参数维度和GBDT规模后，将该IG-GBDT算法用于载荷单机状态识别问题，利用训练集中的样本数据训练载荷单机状态判别模型，再利用测试集中的样本数据验证该模型效果。训练所得模型对训练数据和测试数据的分类结果如表1和表2所示，表示5种模式预测结果和真实值之间的关系。其中，训练集准确率为99.36%，测试集的准确率为99.27%。由混淆矩阵可知，IG-GBDT算法对于各个模式都能较准确地进行识别。

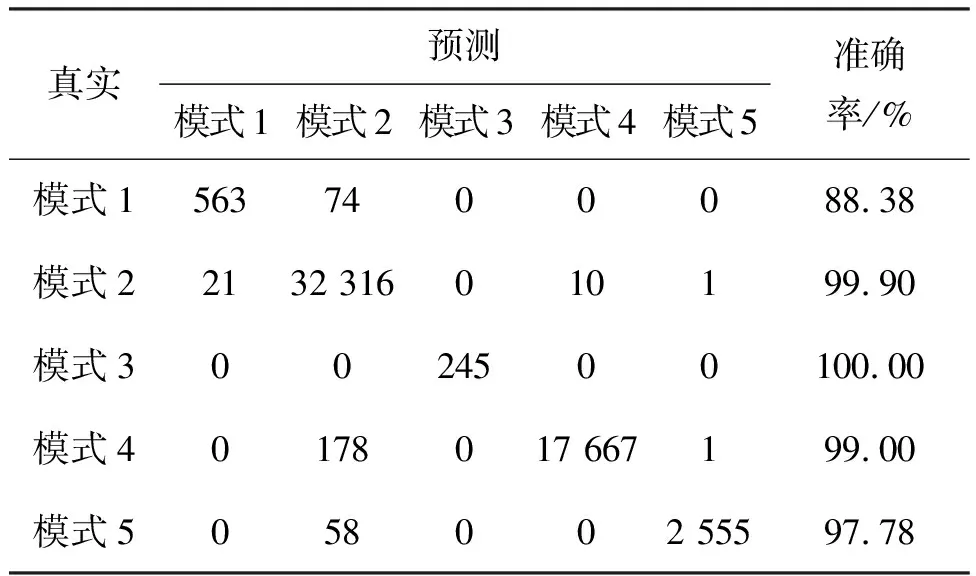
表1 IG-GBDT算法-训练集混淆矩阵

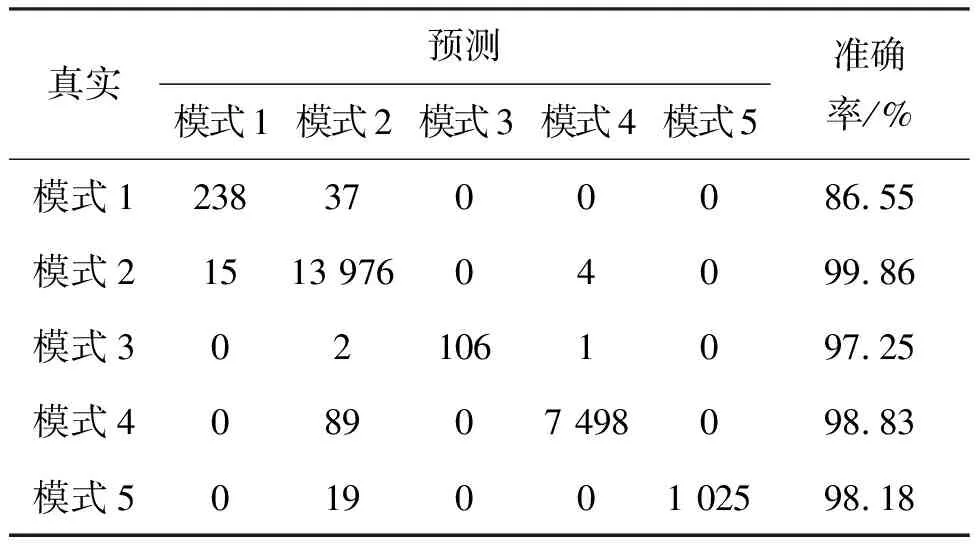
表2 IG-GBDT算法-测试集混淆矩阵

3.3 IG-GBDT与PCA-GBDT算法结果对比

将IG-GBDT算法与基于PCA特征提取的GBDT算法(PCA-GBDT)对比，考虑到数据分布不均衡，采用F1值来进行模型精度的衡量，两种算法的F1值对比如图6所示。

图6 F1值与特征参数维度的关系Fig.6 Relation between F1-score and feature dimension

由图6可知，随着筛选的特征参数维度增加，两个算法的拟合精度均有提升。当维度p=6时，IG-GBDT算法的精度达到最大值，随着参数的增加，其F1值不再显著变化，这与3.2节中所得结论一致。对于PCA-GBDT算法，当特征参数维度p=12时，其精度达到最大值，算法精度不再随p值的增加而提升。两条曲线在达到各自的最优值之后，继续增加p值，会引入冗余特征，因此曲线不再有上升的趋势。对比两种算法最优情况下的F1值，两者的最优F1值基本相同，但IG-GBDT能够用非常少的特征去表征问题，为了达到同样的效果，PCA-GBDT则要用2倍的参数量。

有效载荷单机状态判别对时效性提出了较高的要求，因此对IG-GBDT和PCA-GBDT算法执行效率进行了对比。图7为IG-GBDT和PCA-GBDT算法运行时间随特征参数维度p的变化情况，特征参数增多时，两种算法的运行时间均在不断增加，PCA-GBDT相比IG-GBDT的运行时间增长较慢。结合图6和图7，当两个算法准确度达到最优时，IG-GBDT的参数维度为p=6，PCA-GBDT的参数维度为p=12，此时IG-GBDT的运行时间为56 s，PCA-GBDT的运行时间为175 s，可见在相同的准确率下，PCA-GBDT耗时是IG-GBDT的3倍。因此，IG-GBDT算法较PCA-GBDT算法具有较高的执行效率。

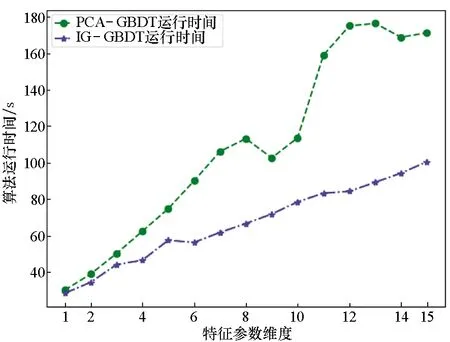
图7 算法运行时间与特征维度的关系Fig.7 Relation between runtime and feature dimension

对比上述IG-GBDT和PCA-GBDT两种方法。首先，二者均能准确判别载荷单机状态，而IG-GBDT筛选出的特征数更少，计算资源消耗少，处理速度快，更能满足有效载荷在轨状态快速识别对时效性的要求；其次，PCA特征降维会对原始遥测参数进行组合，这样改变了参数的含义，不具可解释性，无法对载荷参数进行人工一致性验证，而IG筛选得到的特征参数能确定载荷运行状态判别对应的载荷遥测参数，模型结果具有可解释性；再次，IG-GBDT所得到的特征参数集，可供地面运控系统重点监视参数选择。

4 结论

本文提出了一种基于载荷遥测参数数据的载荷状态判别方法，将多标签分类集成学习方法应用到载荷设备状态识别问题，并采用真实卫星任务数据进行了应用验证。首先，根据载荷按分包遥测抽取遥测原始数据和任务数据，经合并、解析、数值转换等处理得到数据样本集。其次，在对遥测数据野值剔除的基础上，分别构建遥测参数特征向量和载荷标签特征向量，并以星上时为基准分段对标得到特征集，分析实际问题对多标签特征进行转化，根据特征样本集统计量性质筛选特征和降维，计算遥测数据特征数据集对标签特征的信息增益并排序，用于构建样本最终的特征向量集。再次，利用各样本的特征向量训练基于IG-GBDT集成学习的载荷状态判别模型。通过量子科学实验卫星任务真实数据验证，本文提出的IG-GBDT算法具有很高的状态识别准确率。本文提出的载荷状态判别模型和方法能在不依赖于载荷复杂背景知识的情况下适用于载荷遥测数据量大、参数众多、样本分类不平衡等问题，基于IG的参数特征降维和集成学习模型将可解释性和拟合效果好的优势相结合，能满足航天任务的高准确度要求，在实际应用验证中表现出良好的性能和适用性。