预腐蚀铝基复合材料疲劳寿命的预测方法
2021-12-13陈亚萍曾本银喻溅鉴
陈亚萍,曾本银,喻溅鉴,袁 璐
(1. 中国直升机设计研究所,景德镇 333001; 2. 上海航空材料结构检测股份有限公司,上海 200000)
碳化硅增强铝基复合材料是一种金属基复合材料,具有比强度高、比刚度高、密度低和疲劳性能良好等特点,在航空领域应用广泛,如美国F-16战机的腹鳍,Boing777商用飞机PW4000系列发动机的导流叶片等。在直升机领域,该复合材料成功用于EC-120直升机的旋翼连接件和NH90直升机的动环与不动环等零部件,首次实现了在航空一级运动零件上的使用[1-3]。近年来,国内直升机关键零部件也逐步采用该材料。
铝基复合材料结构在使用环境中会产生腐蚀损伤,胡津等[4]研究了铝基复合材料的腐蚀形成机理;陆峰等[5]针对不同铝基复合材料的腐蚀行为进行了研究;王春雨等[6]分析了不同铝基复合材料的腐蚀特点,并提出相应的腐蚀防护措施。本工作通过腐蚀试验,统计分析了直升机铝基复合材料结构的腐蚀形貌特征,分析其与腐蚀时间的规律。
腐蚀会影响铝基复合材料结构的疲劳性能及疲劳寿命,韩忠英等[7]基于损伤演化律研究了腐蚀疲劳寿命预测方法,并对FG20钢和LY12CZ材料的腐蚀疲劳寿命进行了预测,结果表明不同材料的腐蚀疲劳损伤演化参数相差较大。高文欢等[8]基于遗传神经网络,预测了预腐蚀铝合金疲劳性能与预腐蚀试验温度、预腐蚀时间的关系。但尚未有铝基复合材料结构预腐蚀后疲劳寿命预测的相关研究。本工作基于疲劳缺口系数和断裂力学等效应力强度因子,根据铝基复合材料结构腐蚀特征建立模型,预测其预腐蚀后的疲劳寿命。
1 铝基复合材料的腐蚀特征参数
研究表明,铝基复合材料的腐蚀特性与基体合金的一致,即点蚀是其腐蚀失效的主要原因,但相对于铝合金,铝基复合材料的腐蚀坑更多、更小且分布更均匀[4-6]。采用3.5%(质量分数,下同)NaCl水溶液对铝基复合材料试件进行腐蚀,腐蚀形貌如图1所示,可见随着腐蚀时间的延长,腐蚀特征趋于明显。

(a) 6 h

(b) 12 h图1 铝基复合材料在3.5% NaCl溶液中预腐蚀不同时间的表面宏观形貌Fig. 1 Surface macro morphology of aluminum matrix composites pre-etched in 3.5% NaCl solution for different times
对腐蚀坑尺寸以及分布等缺陷尺寸参数进行统计,腐蚀坑深度d与腐蚀时间t的变化规律在工程上可采用幂函数表达,见图2[9]。
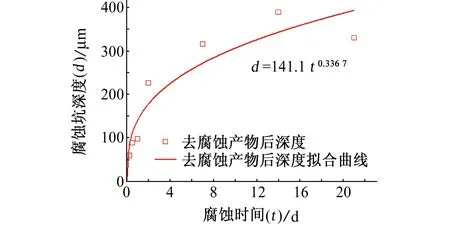
图2 腐蚀坑深度与预腐蚀时间的关系Fig. 2 Relationship between corrosion pit depth and pre-corrosion time
2 基于疲劳缺口系数的疲劳寿命预测方法建模
2.1 应力集中系数随腐蚀坑表征参数的变化规律
铝基复合材料预腐蚀疲劳试验后的断口分析结果表明,当腐蚀坑特征参数达到一定程度时,腐蚀坑成为一个潜在的疲劳裂纹源。当构件表面存在点蚀群时,对构件表面有效应力集中系数起控制作用的是深度最大的那个点蚀坑[10-11]。将点蚀坑简化为半椭球腐蚀坑,形状尺寸见图3。
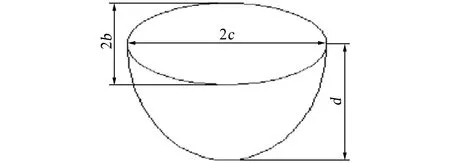
图3 半椭球点蚀坑的形状及尺寸Fig. 3 Shape and size of semi-ellipsoidal pitting pit
单轴拉伸条件下,根据含半椭球形腐蚀坑缺陷试样的应力集中系数规律[12],可得到不同形状点蚀坑的应力集中系数Kt,当b/c时,改变直径2c及深d,即以深径比d/2c为参数,拟合得到Kt:

(1)
2.2 基于疲劳缺口系数的预腐蚀疲劳寿命预测
由前述可知,腐蚀坑表征参数随时间变化,应力集中系数又与腐蚀坑表征参数相关,因此可以得到不同腐蚀时间下的应力集中系数Kt(t)。
采用Peterson近似公式,计算得到不同腐蚀时间的疲劳缺口系数Kf(t):

(2)
式中:p=0.025 4(2 079/σb)1.8,为材料常数,r为腐蚀坑底部曲率半径。
直升机材料结构的疲劳性能通常采用指定应力比R0下的三参数Stromeyer方程表征,因此,指定应力比R0下,不同腐蚀时间对应的材料结构的S-N曲线为:

(3)
式中:Smax,R0为指定应力比R0下,疲劳寿命为N时材料能承受的最大应力;S0(t)为指定应力比R0下,不同腐蚀年限t下的疲劳极限;A,α为疲劳曲线的形状参数;Kf(t)为疲劳缺口系数;S0为指定应力比R0下材料未腐蚀时的疲劳极限。
按最小二乘法可得S-N曲线形状参数及其与试验数据的相关系数。
由于试验过程中一般只进行指定应力比R0下的疲劳试验,因此试验中测得的是指定应力比R0下的S-N-t模型,为使测得的曲面模型适用于不同应力比,利用古德曼方程进行修正:

(4)
式中:Sa和Sm分别为任意应力比下的应力幅值和应力均值;S-1为对称循环载荷下的疲劳极限;σb为材料的强度极限。
根据应力比R的定义有:
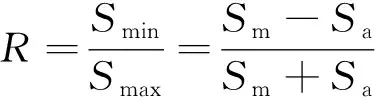
(5)
式中:Smin和Smax分别为最小和最大应力值。变换上式得:
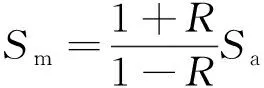
(6)
得到指定应力比R0下的古德曼方程为:
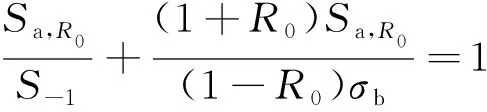
(7)
式中:Sa,R0为指定应力比R0下的应力幅值。
根据上式得到
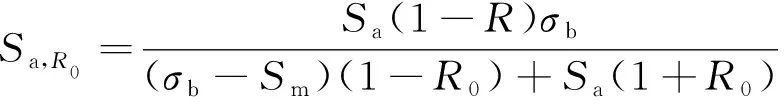
(8)
同理,指定应力比R0下最大应力的方程为:

(9)
得到任意应力比下材料预腐蚀疲劳特性的S-N-t表征模型:
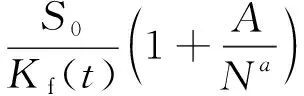
(10)
根据上式即可预测给定应力比、预腐蚀时间、某一载荷下结构的寿命。
3 基于断裂力学等效应力强度因子的疲劳寿命预测方法建模
3.1 腐蚀坑应力强度因子计算
基于断裂力学的疲劳寿命预测方法是将材料表面腐蚀坑,沿着垂直于外载荷的方向进行投影处理,采用等效面积方法,将腐蚀坑简化为半椭圆表面裂纹或半圆形表面裂纹,如图4所示[13-17]。

图4 半椭圆表面裂纹示意图Fig. 4 Schematic diagram of semi-elliptical surface crack
在拉伸载荷作用下,其应力强度因子可表达为:
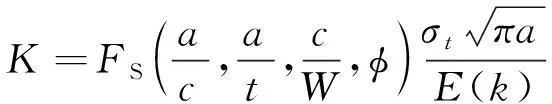
(11)
上式的适用范围为:0≤a/c<2,c/W<0.25,0≤φ≤π/2。
且a/t同样应满足下述条件:当0≤a/c<2时,a/t<1.25(0.6+a/c);当0.2≤a/c≤∞时,a/t<1。
表面裂纹的几何修正函数记作FS,且有
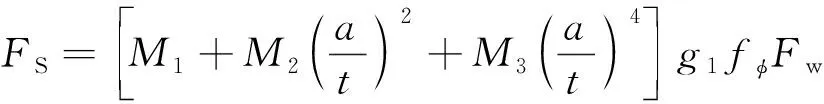
(12)
式中各系数分a/c≤1、a/c>1两种情况给出。
当a/c≤1时,有

(13)
当a/c时,有

(14)
其余各函数,即Fφ、Fw和E(k)由下式给出:

(15)

(16)
此处需要注意的是裂纹尺寸a、c一般不大,故若W很大,则有限宽修正系数fw趋近于1。
第二类椭圆积分E(k)一般查表可得,为便于计算,E(k)可用数值拟合法近似表达为

(17)
上述近似表达式的误差小于0.13%。
3.2 材料的da/dN-ΔKeff基线
应力强度因子幅度ΔK是控制裂纹扩展的主要参量,即da/dN-ΔK存在一定的函数关系,最基本的为Paris公式:
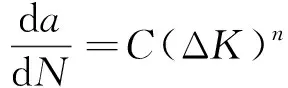
(18)
式中:N是疲劳寿命,a为裂纹长度,C和n是材料常数,由试验确定。
引入裂纹张开函数f,常幅载荷下裂纹张开应力方程见式(19):

(19)
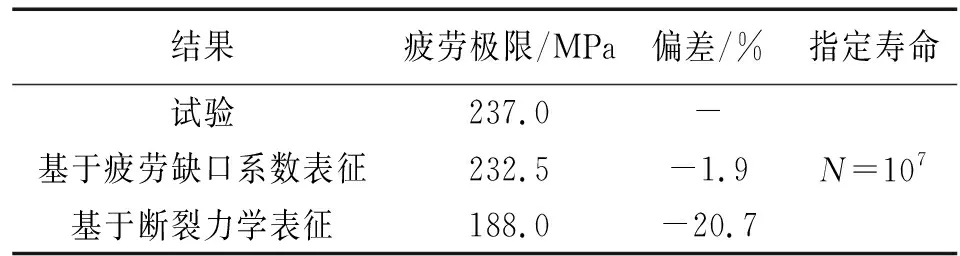
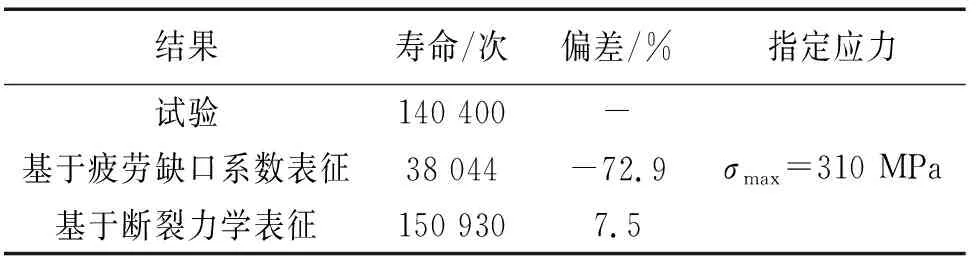
式中:R=Smin/Smax,Smax<0.8σ0,Smin>-σ0,S0=Smin(当S0/Smax (20) 式中:α=1~3为平面应力/应变约束因子;F=1+0.22(a/W)2为有限宽度修正因子;σ0为流变应力(此处定义为屈服应力和极限应力的平均值);KOP为裂纹张开应力强度因子。 当K>KOP时裂纹是张开的,此时有效应力强度因子幅度ΔKeff定义为: ΔKeff=Kmax-KOP (21) 当R≥0时,Smax/σ0对裂纹张开函数的影响较小,因此取其平均值0.3直接带入公式进行分析。采用不同应力比R的da/dN-ΔKeff曲线的分离程度来估计闭合模型的约束系数α,选取约束系数试算法,使得所有系数归并到几乎一条da/dN-ΔKeff曲线上。 对于表面裂纹和角裂纹的扩展,推导得到裂纹闭合系数βR,其表达式为: βR=0.9+0.2R2=0.1R4 (22) 对于表面裂纹,在裂纹前缘与自由表面相交处的ΔK值要乘以βR;对于角裂纹,在裂纹前缘与板的自由表面与孔或缺口表面的相交处两点的ΔK值则都要乘以βR。 进行裂纹扩展寿命估算时,最终裂纹长度αf经常是未知的,必须先确定。 在恒幅循环载荷下,与Smax对应的Kmax值会随着裂纹的扩展增大。当Kmax值达到相关材料和厚度的断裂韧度Kc时,将在裂纹长度为αc的地方发生失效,该长度即为脆性断裂的临界值: (23) 另外,裂纹扩展还会造成截面面积的损失,因此剩余的无裂纹面积上的应力会增大。在达到Kmax=Kc之前可能会发生完全塑性屈服,这取决于材料及结构几何形状和尺寸。这种情况最可能发生在具有低强度和高断裂韧度的塑性材料中。此时可在完全塑性行为的基础上估算临界值α0。 αf是αc和α0中较小的一个。 考虑到裂纹扩展速率Kth存在于低扩展区域,Kc存在于高扩展区域,没有采用方程式对裂纹扩展速率与ΔKeff进行关联,而是使用da/dN-ΔKeff数据表,以便更为精确地描述极限数据,对疲劳寿命进行预测。 在进行裂纹扩展分析时,α值不是均匀分布的,而是aj+1=laj(j=1…n),l≈1.10。 通过这三个点的抛物线下方的面积可由下式给出: [yjl(2-l)+yj+1(l+1)2+yj+2(2l-1)] (24) 根据上式即可预测给定应力比、给定预腐蚀时间某级载荷下的材料的寿命。 将铝基复合材料试样浸泡在3.5%的NaCl溶液中腐蚀7 d后,按疲劳试验标准开展应力比R=0.5的疲劳试验。腐蚀坑的直径、深度见表1。 表1 预腐蚀疲劳试样的断口分析统计结果Tab. 1 Statistical results of fracture analysis of pre-corrosion fatigue sample 根据基于应力集中系数的预腐蚀疲劳寿命预测模型,预测得到在3.5% NaCl水溶液预腐蚀7 d后铝基复合材料的S-N曲线,并将其与试验结果进行比较,结果见图5。可以看出,预测结果与试验结果吻合较好。 图5 两种疲劳寿命预测方法预测的S-N曲线与试验数据对比Fig. 5 Comparison between S-N curve predicted by two fatigue life prediction methods and experimental data 许多试验研究证实,对于不含腐蚀预损伤的航空铝合金而言,绝大部分疲劳寿命,即(80~90)%Nf,是消耗在初始长度为10~20 μm的小裂纹向长裂纹扩展的阶段。因此,基于断裂力学的疲劳寿命方法预测时,假设裂纹从第一个循环就开始扩展而忽略裂纹的萌生寿命,这种假设是可行的。同时,由表1可以看出,腐蚀坑的深度已远远超过了小裂纹的范围,这说明基于断裂力学的裂纹扩展从理论上是可用来预测预腐蚀寿命的。 对铝基复合材料,参考基体材料的铝合金裂纹扩展速率和门槛值的结果,假设涉及应力强度因子门槛值计算式的材料常量为Smax/σ0=0.3,α=1.73,通过裂纹闭合模型得到材料的da/dN-ΔKeff基线拟合线。 利用da/dN-ΔKeff基线,采用数值积分进行计算裂纹扩展寿命。预测在3.5% NaCl水溶液预腐蚀7 d试样的疲劳寿命与实际试验结果的比较如图5所示,预测结果与试验结果吻合较好。 对直升机典型高周疲劳段(N>106),基于疲劳缺口系数表征预测的疲劳寿命与试验值更接近;N=107次对应的条件疲劳极限见表2,基于疲劳缺口系数表征预测的与试验值偏差为-1.9%。 表2 指定寿命下预测疲劳极限与试验疲劳极限对比Tab. 2 Comparison of predicted fatigue limit and test fatigue limit under specified life condition 对低周疲劳段(N<106次),基于断裂力学等效应力强度因子表征预测的疲劳寿命与试验值更接近。σmax=310 MPa时,基于断裂力学等效应力强度因子表征预测的寿命与试验寿命偏差为7.5%,见表3。 表3 指定应力下预测寿命与试验寿命对比Tab. 3 Comparison of predicted life and test life under specified stress condition 将腐蚀缺陷等效成疲劳缺口,基于疲劳缺口系数表征建模,同时基于模拟裂纹的断裂力学等效应力强度因子表征建模,预测预腐蚀后试样的疲劳寿命。与铝基复合材料预腐蚀后的疲劳试验数据进行对比分析验证,结果表明: (1) 两种模型的预测结果与试验结果偏差均在可接受范围,两种疲劳寿命方法预测方法均是合理可行的。 (2) 基于疲劳缺口系数表征的寿命预测方法在高周疲劳段与试验值更接近,其高周疲劳性能强度偏差在4%以内,可用于确定直升机高周疲劳结构件腐蚀缺陷容限尺寸和腐蚀缺陷检查周期等。 (3) 基于断裂力学等效应力强度因子表征预测结果在低周疲劳段与试验值更接近,可用于直升机低周疲劳结构损伤容限设计。
3.3 基于有效应力强度因子的预腐蚀疲劳寿命预测
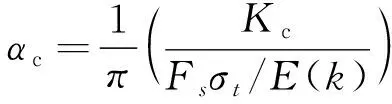
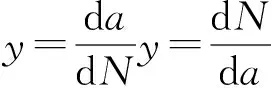
4 模型方法验证

4.1 基于疲劳缺口系数的疲劳寿命预测方法

4.2 基于断裂力学等效应力强度因子的疲劳寿命预测方法
4.3 两种疲劳寿命预测方法比较
5 结论
