WC-10Ni/NiCrBSi复合涂层剪切强度及数学模型建立
2021-12-13贡泽斌许祥平邹家生
贡泽斌,许祥平,何 力,邹家生
(江苏科技大学 材料科学与工程学院,镇江212100)
硬质合金的成分组成与合金硬度和强度的关系一直是国内外学者研究的重点[1-2].硬质合金成分的繁杂性和制造工艺的多样性对涂层结合强度的综合影响,难以使用现有的理论来统一解释,并且大多数情况下只能通过大量的实验进行总结,这将需要花费大量的人力物力.因此,找到一种合理的数学模型将涂层影响因素参数化并预测出成分对涂层结合强度的规律显得亟为重要.
多年以来,国内外学者对硬质合金结构参数化及其数学模型的建立进行了一定的探索.文献[3]利用MATLAB软件和Python语言编程建立基于“随机法”的二维微观WC-Co结构,将影响结构的因素参数化,达到了预期值与实际值相吻合的目的,但由于二维微观模型过于复杂,不适合工程实际.文献[4]建立了WC-Co的有限元模型,定量剖析Co含量的变化以及 WC晶粒度对其力学性能的变化,验证了数学模型法测量硬质合金力学性能的可行性,但精确度不够准确.文献[5]假设了在涂层内部残余应力由硬质相WC向粘结相Co传递,分析得出涂层粘结相Co中的应力超过临界值后,涂层发生屈服变形,并建立了相应的数学模型,但是涂层的数学模型涉及到的微观参数需要测量,测量手段费事费力且经济性差.
针对上述硬质合金结构参数化及数学模型建立研究中存在的问题,文中以真空钎焊WC-10Ni/NiCrBSi复合涂层为研究对象,研究其内部微观结构与剪切强度间的影响关系,通过拟合计算得出涂层的参数化模型.将复合涂层实际剪切强度与模拟数据对比,用于检验数学模型的精准度.然后通过拟合计算复合涂层的微观结构因素来化简微观测量参数的数量,探究不同的硬质相WC与钎料配比下,复合涂层剪切强度变化的影响规律.
1 复合涂层剪切强度的数学模型
1.1 WC-10Ni/NiCrBSi涂层参数分析与模型理论
真空钎焊制备涂层时,其内部存在一定量的孔隙.孔隙的存在对涂层与基底的结合强度有较大的影响[6],其内部孔隙率越大,结合强度就越低[7].白点理论认为硬质合金内部截面存在着细小的“平滑区域”其中存在柯式Co气团、孔隙与粗晶WC[8].“平滑区域”的抗弯强度以及发生断裂的位置直接决定了涂层与基底的结合强度.通过预先进行的剪切实验中发现,断裂发生的位置主要集中在复合涂层内部的WC相与Ni相结合的边界处[9].对复合涂层的微观组织结构进行扫描电镜分析,发现WC颗粒排列紧凑且WC大部分表面包覆着粘结相(图1),说明复合涂层的内部微观合金结构与“薄膜理论”相吻合.显然涂层的断裂强度是与涂层内部的孔隙、微裂纹有关[10],因此建立复合涂层剪切强度的数学模型时,既要考虑涂层内微结构的物理性能,也要考虑不同相之间的界面物理化学特性[10].
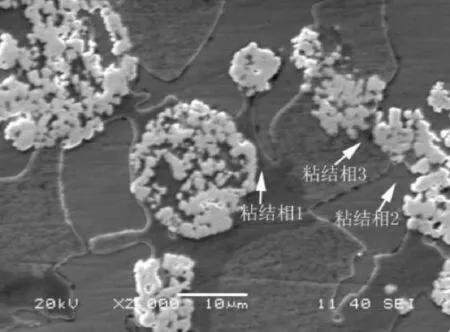
图1 WC表面的粘结相扫描结果
复合涂层的结合强度大小与硬质相WC的含量呈反比关系,并且制备过程中复合涂层内部存在的空隙,也会影响涂层的结合强度,孔隙的大小(孔隙的平均面积S)对结合强度影响最大.在本涂层中是以软粘结相NiCrBSi为基体的,WC的含量以及涂层中各相的物理性能会影响最终的结合强度[11].其中粘结相NiCrBSi的弹性模量ENi、硬质相WC的弹性模量EWC、WC的体积分数fWC、NiCrBSi的体积分数fNi、涂层孔隙率φ与结合强度之间的数学关系为:
(1)
WC晶粒度越小,粘接相与WC颗粒接触的越致密,一个单位颗粒上的粘接力也会上升[12].所以降低WC晶粒度便可增加硬质相与粘结相的接触数量,以提高涂层的剪切强度.对WC晶粒度d与剪切强度间的关系式为:
(2)
WC/WC邻接度、WC和粘接相是涂层内部的结构对复合涂层的剪切强度的影响因素.涂层中硬质相WC的抗拉强度GWC,钎料NiCrBSi的抗拉强度GNi是其内部结构影响结合强度的体现.综合强度理论[13]认为:复合材料的物理性能取决于各组成相之间的性能匹配,这也符合了WC薄膜理论.因此WC/WC邻接度C与 WC的体积分数fWC间的关系:
(3)
由上述公式得出的结论,拟合出能反映各因素对复合涂层剪切强度影响的数学模型:
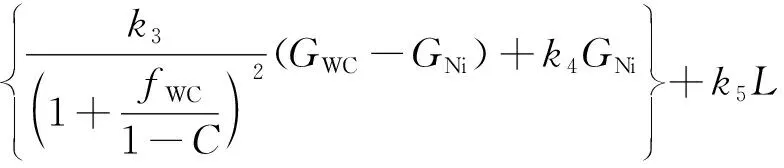
(4)
公式(4)第一项体现了涂层孔隙和复合材料弹性模量对涂层结合强度的影响;第二项体现了WC颗粒晶粒度大小对涂层结合强度的影响;第三项体现了WC/WC的邻接度、WC和Ni相的抗拉强度对涂层结合强度的影响;第四项体现了涂层与基体结合层宽度对涂层结合强度的影响.上述四项通过相应的限制系数k进行控制.WC的弹性模量EWC、NiCrBSi的抗拉强度GNi、NiCrBSi的弹性模量ENi、WC的抗拉强度GWC为定值,需测量式(4)中的涂层孔隙率φ、空隙面积S、WC/WC的邻接度C、涂层与基体结合层宽度L、WC平均晶粒度d.
1.2 涂层制备以及有关参数的测量
在Q235基体表面使用真空钎焊工艺进行涂层熔覆,采用BNi-2钎料布,钎料的厚度控制在2~3 mm,确保真空钎焊设置焊接工艺相同[14].为了体现出WC对涂层参数的影响而选择把涂层中WC的含量控制成30%、50%、80% 3种,以达到避免出现测量结果数值较为集中的效果.涂层的冶金过程如图2:硬质层与钎料布叠放置于基体材料上,随着温度的升高导致钎料的熔化、粘接剂的挥发,WC颗粒伴随着流淌混入表面熔覆层.最终熔覆层冷却凝固形成基体表面的硬质涂层.

图2 涂层在真空钎焊中的冶金过程
制备完毕复合涂层后对涂层取截面,得到涂层内部结合层的金相组织图像并且利用ImageJ软件中的二值化功能对其“调校二值化图像”.调整到合适的二值化图像,图像处理结果如图3.通过ImageJ软件分析数据中的自动测量功能测量涂层图像的加深阴影图像面积,处理结果标注了涂层的孔隙与孔隙占总涂层面积的比例.孔隙率和孔隙平均面积大小见表1.

图3 涂层截面测量孔隙面积的处理结果(结合层二值化图像)
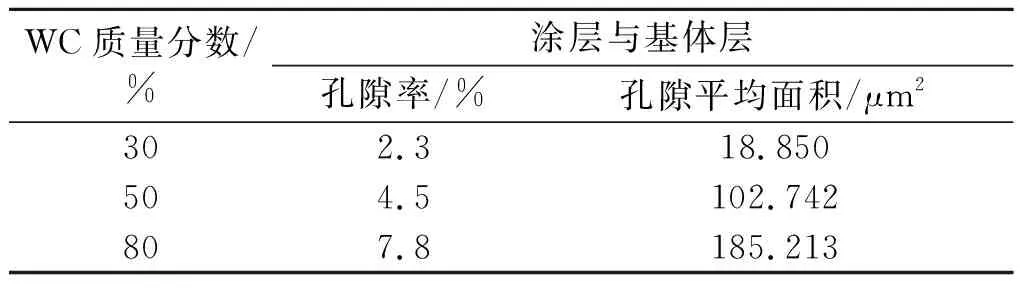
表1 复合涂层孔隙率与孔隙平均面积数据
复合涂层的WC表面为疏松多孔状,传统测量方法如截线法、网格法无法测量.截线法、网格法需要所测的涂层相为均匀质地,WC与粘接相包覆无法准确测量出其单位颗粒的邻接度.此时须引入ImageJ法[15]对WC邻接度间接测量.先测量出WC/WC晶界长度LWC/WC与WC/Ni的相的相界长度LWC/Ni,再通过公式计算得到WC的邻接度.
(5)
在复合涂层的熔覆过程中,较小尺寸WC发生溶解和较大尺寸WC的生长,导致WC的颗粒大小与制备前相比会有所变化,因此使用ImageJ软件确定面积统计范围为80~1 963 μm2更为合理.ImageJ分析计算图如图4,ImageJ计算结果见表2.

图4 WC涂层LWC/WC与LWC/Ni+2LWC/WC处理图

表2 涂层内部晶界长度的测量结果
依据上述分析获得涂层的WC相界长度和WC/Ni相界长度测量结果,由邻接度式(5)代入计算涂层的邻接度值(表3).
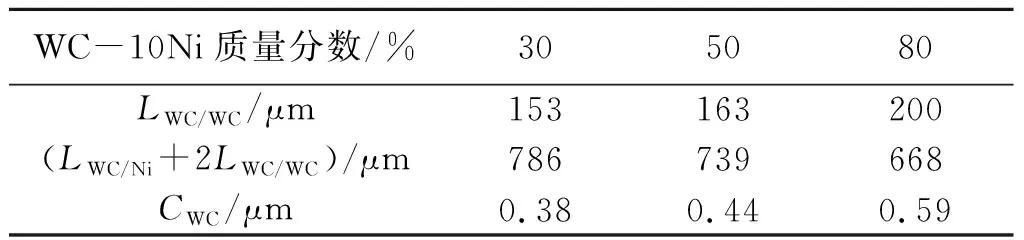
表3 3种WC邻接度
用SEM观察复合涂层的微观形貌(图5).3种复合涂层的结构呈现出分层现象,I区域中所含WC极少,是由于WC颗粒密度大于镍相钎料在涂层冶金过程中WC下沉至另外一个区域,因此I区域中主要体现的是镍相;II区域涂布层中的WC颗粒熔入表面熔覆层后形成的WC-10Ni/NiCrBSi层,此区域内可观察WC与粘接相均匀分布;III区域是钎料中所含Si、B元素沉积在Ⅳ区域Q235基体上用于连接WC-10Ni/NiCrBSi层的连接层,连接层的厚度为所需测量的涂层与基体结合层宽度,测量结果如表4.

图5 所取截面的SEM图

表4 涂层与基体结合层宽度
测量WC晶粒度dWC时,有些孔隙的形状与大小与WC颗粒相似会导致软件无法正确识别出孔隙和WC颗粒因此在测量前利用图像修改软件手动剔除孔隙来提高结果正确度.用二值化图像进行统计分析,分析结果如表5.

表5 3种含量WC平均晶粒度
通过以上实验及分析完成了对孔隙率、空隙面积、WC/WC的邻接度等关于涂层微观参数的测量,将测量结果见表6.
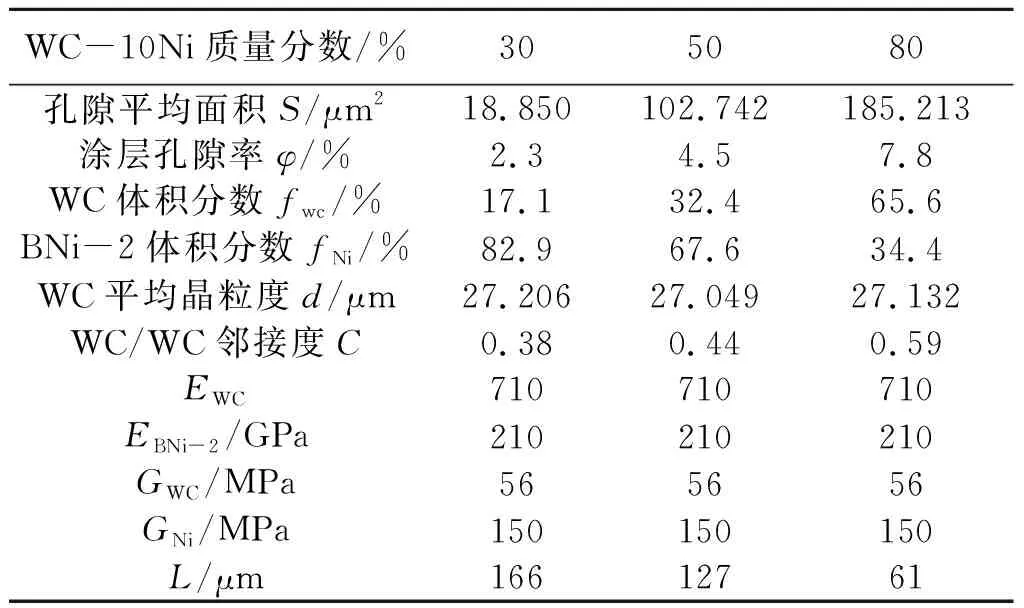
表6 测量复合涂层微观参数表
2 涂层数学模型准确度的检验
将表5中的数据代入式(4)中,k1,k2,k3,k4,k5分别取8.93,146.12,8.45,0.53和3.74.计算得出的剪切强度模拟值如表7.

表7 数学模型计算所得剪切强度模拟数据
利用自制的剪切夹具对3种WC涂层进行剪切试验,剪切实验值如表8.
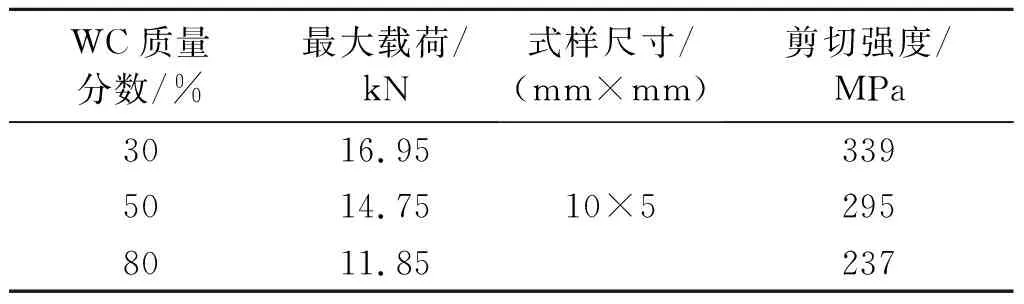
表8 熔覆后的复合涂层剪切实验数据结果
从表7和8中的数据对比来看,该模型预测值与实际值吻合度较好,基本上与涂层实际剪切强度相近,同时反映出了复合涂层剪切强度与WC质量分数的关系(见图6).
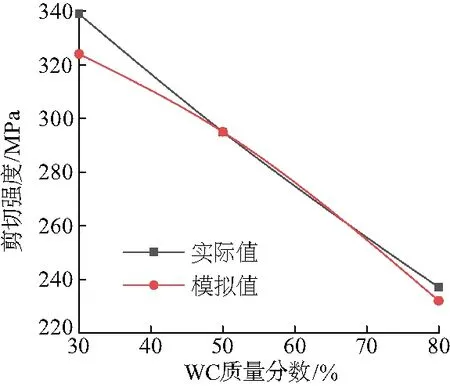
图6 实际值与理论值的对比
3 涂层剪切强度参数化模型的改进
从式(1~4)的涂层参数化模型来看,该复合涂层剪切强度数学模型所涉及的微观参数多,需要对参数化模型中的每一个数据进行测量.为简化并准确地对不同WC质量分数的复合涂层剪切强度进行预测,需将参数化模型提出进一步的修改.
复合涂层的剪切强度与式(1)中的多个因素有关:孔隙率φ和WC的质量分数w存在数量关系.WC颗粒越多造成的与粘接相接触变少直接导致了孔隙率的增加.将涂层孔隙率φ简化为与WC质量分数有关的定量关系:
φ=0.1w(WC)
(6)
孔隙的平均面积S会与WC的质量分数w(WC)有关,对孔隙的平均面积S进行拟合计算:
S=-2 296.1w(WC)3+3 385.2w(WC)2-1 163.8w(WC)+
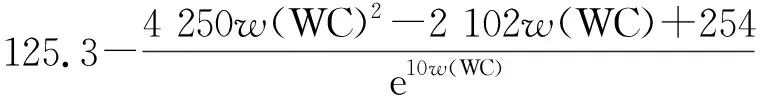
(7)
文献[16]的理论:WC的体积分数fWC与WC/WC邻接度之间存在幂运算上的数量关系.
CWC/WC=0.32e0.92fWC
(8)
涂层与基底结合宽度L是在复合涂层的结构中出现的分层现象.第一层由于WC密度大于NiCrBSi几乎含极少的WC,第二层是WC与NiCrBSi的结合层,是主要体现其力学性能的区域组织.因为硬质相WC在钎料布中熔化与涂层结合,在观察截面SEM形貌中已经得出复合涂层截面结合层厚度即涂层与基底结合宽度L与WC的质量份数w(WC)存在关联,其对应关系具有一定的函数规律,故可利用以下简便计算:
(9)
把式(6~9)的参数关系代入参数化模型(公式(4))中,就获得了变量仅有WC的质量分数与体积分数的涂层剪切强度数学模型,化简整理为:
(10)
式(10)为复合涂层剪切强度数学模型,自变量控制为WC的质量分数与体积分数两种,减少了原先公式(4)中微观参数的测量,大大提高了计算速度.为了确保数学模型的实际准确度,利用自制剪切夹具对10%至80%的WC涂层进行试验.根据式(10)的复合涂层的剪切强度代入对应的WC质量分数,得到的计算结果与复合涂层的实际剪切强度见表9.
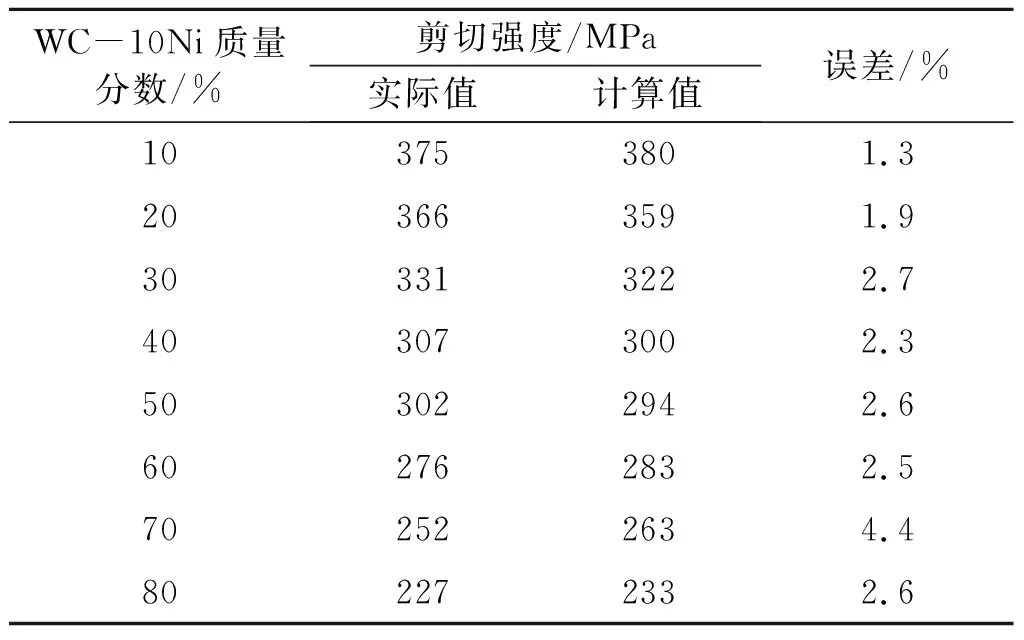
表9 简化数学模拟计算值与实际剪切强度
对比实际剪切强度结果:该复合涂层数学模型的模拟值与实际值相近且数学模型的吻合度高,其模拟值的误差不超过4.4%.反映出了复合涂层剪切强度数学模型精准度良好,直观体现了WC-10Ni/NiCrBSi复合涂层界面结合强度随WC含量变化的趋势(图7).
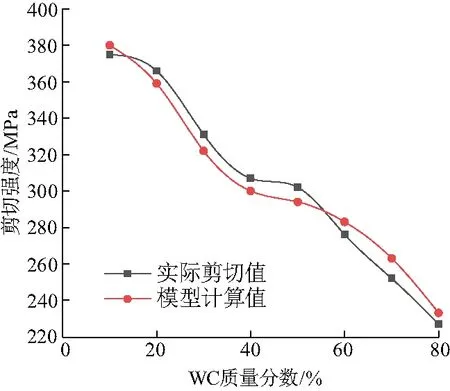
图7 涂层实际剪切值与简化模型预测值的变化趋势
4 结论
(1) 通过真空钎焊将硬质相WC 和钎料布成功熔覆并制备出了WC-10Ni/NiCrBSi复合涂层,涂层微观结构呈现出粘结相包裹WC颗粒的薄膜结构,宏观上呈现WC聚集的骨架结构.
(2) 提出了WC-10Ni/NiCrBSi复合涂层的参数化模型,与复合涂层实际剪切强度相比,吻合度高,预测数据精准.
(3) 经过改进后的复合涂层剪切强度数学模型,误差不超过4.4%,可直观体现出WC-10Ni/NiCrBSi复合涂层界面结合强度随WC含量变化的趋势.
