风电设备对系泊状态下养殖工船稳性的影响分析
2021-12-13张春涛蔡金延丁仕风
张春涛,蔡金延,丁仕风,周 利*
(1.中国水产科学研究院 渔业机械仪器研究所,上海200092) (2.江苏科技大学 船舶与海洋工程学院,镇江 212100)
近年来,海洋牧场成为海洋工程领域的新热点,养殖工船长期远离大陆作业,需要大量的电力维持养殖系统运转.风电装置作为绿色能源,是养殖工船能耗问题的最佳解决方案之一.在养殖工船原有设计基础上添加风电设备,会额外增加设备重量,并产生较大的风电载荷,必然会影响船舶稳性,开展风电设备对系泊状态下养殖工船稳性的影响分析非常重要.
完整稳性是船舶安全性的重要标准,在设计船舶和建造船舶时需要重点考虑的关键性因素.但仍然会有大量船舶由于稳性校核不严谨,出现严重事故.正是如此,国际海事组织(IMO)从上世纪中后期就开始修订各种船舶的完整稳性规范,发展到目前为止,起草了《2008年国际完整稳性规则》,即第一代完整稳性规则[1].
早在18世纪,首次提出了稳心的概念,并定义了稳心半径和初稳性高的概念,从19世纪90年代开始陆续出现学者对横摇现象展开研究,文献[2]对船舶在突风及规则波共同作用下的非线性横摇运动方程展开研究;文献[3]针对船舶在静水中的稳性计算方法与波浪中稳性的计算方法进行区别,对规则波中的船舶稳性展开研究;文献[4]阐述了国内外波浪中船舶稳性的最新进展,以及完整稳性的几种失效模式的研究状况和发展方向;文献[5]研究了完整稳性与过度加速度薄弱性衡准草案理论方法,并进行了大量的样船计算.文献[6]基于经验公式的Level 1衡准和波浪中物面非线性关系影响GZ曲线特征的Level 2衡准方法,对38条不同船型稳性丧失衡准敏感性进行了研究.文献[7]根据工信部完整稳性衡准相关研究成果,介绍了5种失效模式薄弱性能衡准和直接评估的最新进展.文献[8]结合了二代完整稳性5种失效模式特点,提炼并形成了模型试验方法.文献[9]根据第二代完整稳性4种稳性模式的计算分析,研究第二代稳性的实施对大型集装箱船的稳性影响.文献[10]基于波浪补偿技术条件下对第二代完整稳性衡准中参数横摇失效模式进行数值模拟,计算出船艇产生参数横摇时保持稳定平衡的波浪补偿量.文献[11]采用第二代完整稳性衡准中薄弱性衡准方法对2种不同尺度的极地破冰船设计方案开展动稳性敏感性评估,指出了未来优化研究的方向.文献[12]对二代完整稳性中5种失效模式的研究进展进行了综述,同时给出了5种稳性失效模式的第一层薄弱性衡准、第二层薄弱性衡准以及直接评估方法.文献[13]基于二代完整稳性,采用一种离散的船舶转动惯量通用计算方法, 研究了过度加速度薄弱性衡准和稳性直接评估数值模拟方法对于转动惯量计算精度的敏感性.文献[14]发布了二代稳性衡准标准临时指南.目前《2008年国际完整稳性规则》中尚未考虑附加载荷的影响.而风机作用可能产生横倾力矩,从而对船舶稳性安全产生负面影响,目前这方面研究学术界和工业界都没有开展过.
文中首次基于现行稳性衡准的力学背景,定量研究风电载荷对养殖工船的影响.通过分析影响系泊状态下船舶稳性的参数,基于COMPASS软件,构建船舶模型,计算不同风电安装位置下,风电设备工作时,对船舶稳性造成的影响,并分析造成影响的原因以及稳性衡准值的变化范围,核算安装风电设备之后是否还满足法规要求.然后借助COMPASS_WALCS波浪运动和载荷直接计算软件,计算由于波浪作用产生的横摇角,将结果与经验公式相比较,进行不同计算方法对波浪引起横摇角的敏感性分析.
1 稳性分析力学模型
1.1 风电载荷力学模型
风电设施在发电工作时可以视为作用在船舶甲板上安装点位置处的一个任意方向的力矢量.这个力矢量的大小可以在30~50吨力范围内浮动,安装点位置可以是甲板上任意位置,力矢量的指向可以是指向天空的任意方向,F(x,y,z)为风电设备合力矢量;α为合力F与xoy平面的夹角;β为合力F与xoz平面的夹角;Fx,Fy,Fz分别为合力投影到各个坐标上的分量.
1.2 风电载荷基本假定
基于静力学的稳性衡准对于船舶稳性评估的基本假定为:假定船舶在静水当中忽略波浪对于自由表面的影响,采用自由纵倾原理(即运动自由度仅考虑吃水和纵倾)计算不同横倾角下的GZ曲线值,校核风力载荷和波浪载荷影响下船舶的稳性是否满足衡准要求.静力学中对船舶运动自由度仅考虑横倾纵倾和升沉3个自由度.
我国现在船舶稳性衡准要求是按照中华人民共和海事局颁布的《国际航行法定检验技术规则(2008)》附则3[1]中关于国际海事组织文件包括的所有船舶的完整稳性规则进行计算和校核.其中对渔船单独做出衡准要求:
(1) 初重稳距要求
在各种装载工况下经自由液面修正后的初稳性高度应不小于0.15 m.
(2) 复原力臂曲线下的面积要求
除另有明文规定外,在任何装载工况下,复原力臂曲线(GZ曲线)下的面积应满足下列要求:
至横倾角φ=30°时,应不小于0.055 m·rad;
至横倾角φ=40°或进水角φf(如φf<40°)时,应不小于0.090 m·rad;
在横倾角30°~40°或30°与φf(如φf小于 40°)之间,应不小于0.030 m·rad;其中,φf为船体、上层建筑或甲板室的开口不能迅速关闭成风雨密而开始进水时的横倾角.
(3) 气象衡准值要求
船舶抵抗横风和横摇联合作用的能力曲线如图1.
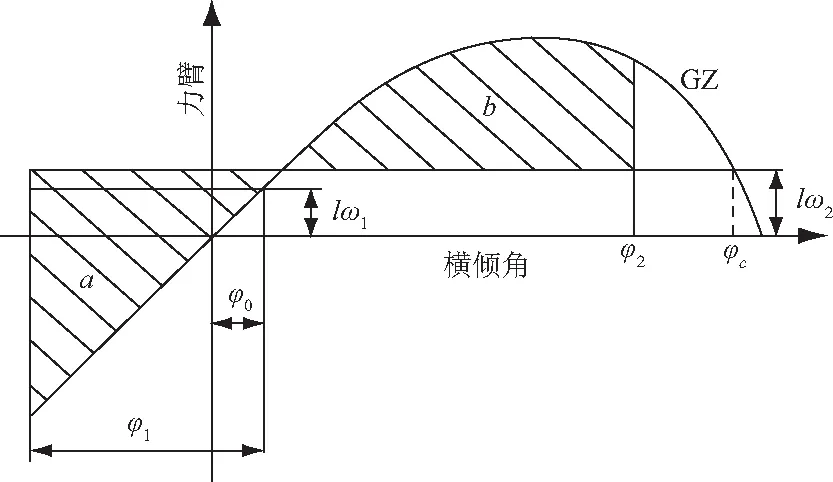
图1 突风与横摇
船舶受到垂直于其中心线的一个定常风压的作用,产生一个定常风倾力臂lw1,假定由于波浪作用假定由于波浪作用船由平衡角φ0向上风一侧摇至一个横摇角φ1,在定常风作用下的横倾角)应不大于16°或甲板边缘浸水角的80%,取较小者,然后船舶受到一个阵风风压,产生一个阵风倾侧力臂lw2,在此情况下,面积b应该大于等于面积a,即气象衡准值应该大于1.
根据船舶完整稳性衡准的制定背景,船舶完整稳性衡准基于单一风险源分析原则,仅考虑船舶在水中受到风浪作用下时是否具备充足的抵御外载荷导致倾覆的能力.因此,现有法规中对于船舶完整稳性的规定,一般不直接在GZ曲线施加的倾覆力臂中考虑额外的载荷.在目前规则制定过程中,允许考虑初始横倾角的影响,但对于外载荷则仅考虑风和浪对船体的直接作用.因此,从衡准制定的本源出发,应将风机载荷视为初始横倾角的一个影响因素更合适.
考虑到风电工作载荷在作用点安装位置、载荷空间力矢量方向和载荷大小上存在较大的不确定性,因此有必要研究各种可能情况下风电载荷对于船舶稳性的影响.根据完整稳性衡准的制定原则,可以将风电载荷等效转化为作用在船上的若干力和力矩,并最终转化为若干质量配载的形式进行等效处理.
因船舶进行稳性分析时视为刚体,船舶受到力矢量作用后,可以根据理论力学原理,将其等效为对于船舶重心施加的若干力和力矩的作用.现定义坐标系:坐标系原点与船舶装载工况的重心重合.x轴与基线平行,由原点指向船首,y轴由原点指向船舶左舷,z轴由原点指向天空,坐标系定义满足右手定则.
在上述坐标系下,假定船舶上的力矢量作用点坐标为(x,y,z),力矢量分量为(Fx,Fy,Fz).则作用在重心处的等效力为(Fx,Fy,Fz),等效力矩为(Mx,My,Mz).
Mx,My以及Mz的计算为:
Mx=Fz·y-Fy·z
My=Fx·z-Fz·x
Mz=Fy·x-Fx·y
(1)
根据分析,等效载荷可以进一步等效为施加在船舶上的等效质量配载:
Fz可等效为在重心位置配载的正/负质量;Mx可等效为在重心左/右舷配置一对正/负质量;My可等效为在重心前/后舷配置一对正/负质量.
等效质量可分为3个部分:
(1) ΔM1=Fz/g,坐标为重心处,定义坐标系下坐标为(0,0,0);
(2) ΔM2=±Mx/2yg=±(Fz·y-Fy·z)/2yg,坐标为重心处,定义坐标系下坐标为(0,∓y,0);
(3) ΔM3=±My/2xg=±(Fx·z-Fz·x)/2xg,坐标为重心处,定义坐标系下坐标为(±x,0,0).
计算时需要将不同方向上的等效力(Fx,Fy,Fz)按照上式,进行部分装载,再与各个工况进行组合,形成不同的装载工况,在COMPASS的SRH14的计算模块中进行稳性计算,可得出在ld03工况下,安装在(5,5,21.5)位置上的风机对船舶整体稳性的影响情况.
2 风电载荷对稳性影响分析
2.1 船体模型
采用Compass-Rules软件,Compass-Rules海船规范计算系统作为船级社COMPASS工程计算软件系统一个重要的子系统,广泛应用于船舶审图、规范科研、辅助设计、航海安全评估规范计算和审图计算等领域.涵盖了船舶结构、性能、轮机和电气4个专业的计算模块.此次对船舶稳性计算就是使用了其中的船舶性能模块,根据船舶型线图对船舶进行建模.由型线图可知船长为241 m、型宽45 m的渔船,其型深为21.5 m,吃水为12 m,然后在COMPASS中建立船体模型,如图2.
图2 船体建模
然后根据总布置图在船左舷空旷位置选取6个位置(右舷同理),安装风电设备:
FJ11,坐标(120,20,21.5);
FJ12,坐标(120,16,21.5);
FJ21,坐标(5,5,21.5);
FJ22,坐标(5,0,21.5);
FJ31,坐标(277,4.7,21.5);
FJ32,坐标(277,0,21.5).
文中主要以空载出港(LD1)、满载出港-结构吃水(LD3)、满载出港-设计吃水(LD5)、养殖工况-结构吃水(LD7)4个工况为典型工况,并对其展开计算研究.
2.2 计算模型精度验证
在COMPASS的SRH10模块中对目标船舶进行建模并检验计算模型的正确性.用SRH11模块计算不同装载工况下的浮心纵向位置DLCB、横稳心高HKMT以及排水量的值,主要与LD1、LD3、LD5与LD7工况下的装载手册中的值进行误差分析,如表1.

表1 建模误差分析
由表可以看出,KMT的误差小于2%,LCB的误差小于±1%,排水量的误差小于±0.3%,都满足国际船级社协会(IACS)对于稳性建模误差的标准.
在确认计算模型精度满足后,在SRH14模块中按照装载手册不同装载工况对模型进行配载计算,对计算所得到的吃水值、纵倾以及横稳性初高HGM与装载手册上的对应值进行误差分析,如表2.
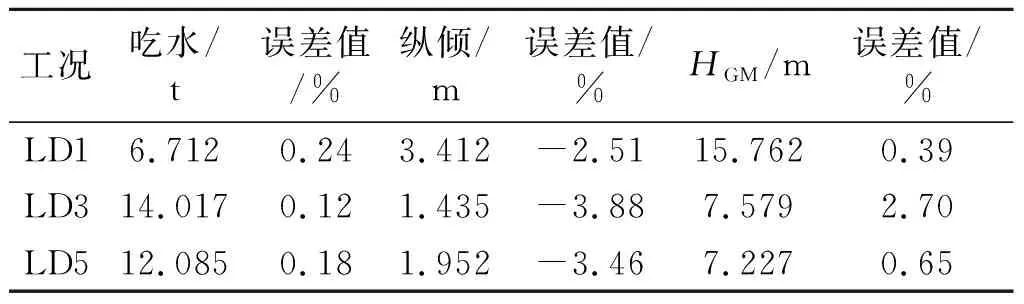
表2 吃水值、纵倾以及HGM误差分析
通过误差对比分析,发现模型船和目标船在不同工况下的吃水、纵倾以及HGM都在可以接受的误差范围,再次确认模型船的可行性.
各项分析对比结果表明,建模具备良好的精度,用于后续风电载荷影响分析所获得的结果将是可信的.
2.3 不考虑风电载荷作用条件下船舶稳性计算
通过计算,验证了模型的精度后,开始对模型船进行风电设备质量配载和稳性.当风电设备不工作时,仅作为静止的质量计入船舶配载,按照上述假定的六个位置作为安装位置,质量计为5 t.则此时可将上述受力分析简化为在(x,y,z)处受力Fz.通过计算得出气象衡准值和稳定风作用下的横倾角,并与装载手册上未安装风电设备时的衡准值进行比较,如表3.
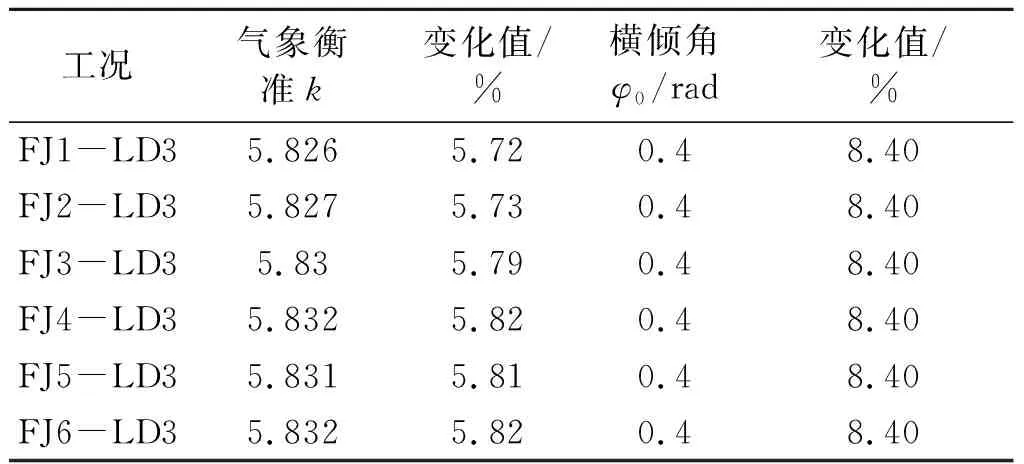
表3 LD3工况下安装风电设备后衡准和横倾角的变化值
从表中可以看出,在安装风电设备之后,船舶稳性计算结果均满足完整稳性规则,且与未安装风电设备时的稳性计算结果相比较,变化值在可接受的范围内.因此,在该位置安装的风电设备对船舶完整稳性影响较小,能够符合法规的要求.
2.4 多方向风电载荷作用条件下船舶稳性计算
当风电设施工作,计入(Fz,Mx,My)的影响,假设在以LD3工况(满载出港-结构吃水)为例,选择最靠近外侧的3个位置安装风电设备,坐标分别为:① FJ1:(120,20,21.5);② FJ2:(5,5,21.5);③ FJ3:(277,4.7,21.5).力矢量(Fx,Fy,Fz)的合力大小在为50 t,力矢量的指向方向在xoy平面上应360°等间距分布,分布间隔60°一个.力矢量的指向方向在xoz平面上应90°等间距分布,分布间隔为60°.按照式(1)进行等效质量计算,然后对模型进行等效质量装载,计算得出初稳性高度HGM、气象衡准值以及稳定风作用下的横倾角,如表4.
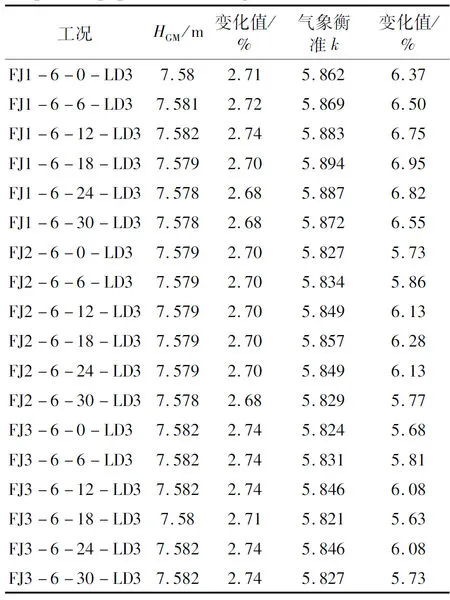
表4 LD3工况下风电设备工作时的船舶稳性计算结果
由表4可知,在风电设备工作的情况下,只有稳定风作用下的横倾角与原先未安装风电设备时的横倾角相比变化较大,其余值变化不超过10%.且在(120,20,21.5)位置时,各个稳性计算值变化更小.
这表明,由于风向改变导致的风力载荷方向的变化确实会对船舶完整稳性的安全水平产生不等的影响.但总体上各项稳性参数改变的绝对值较小,对于稳性安全裕度的改变不大,因此风向的影响总体较小.
2.5 典型环境工况下风电载荷对船舶稳性的影响
在计算了LD3工况之后,进一步研究风电载荷对于其他典型装载工况的影响.选择在LD5工况(满载出港-设计吃水)下进行同样的装载计算,并与装载手册中未装载风电设备时的稳性计算结果相比较,如表5.
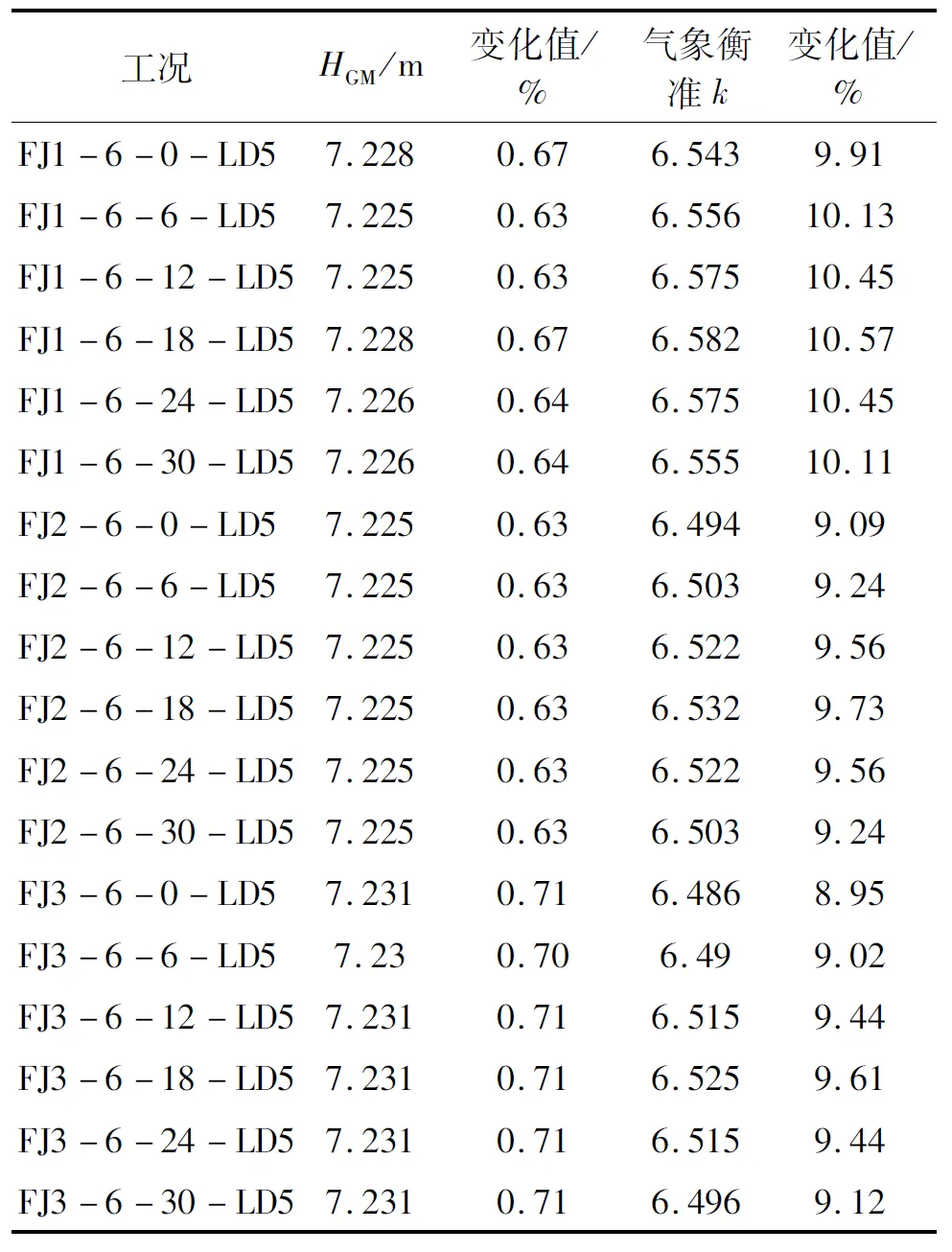
表5 LD5工况下风电设备工作时的船舶稳性计算结果及变化值
由表中可以看出,在LD5工况下安装风机电设备后,风电设备工作状态下的船舶稳性计算结果依然满足稳性衡准要求.总体上,考虑不同典型环境工况下的风电载荷对于本船典型装载工况的稳性产生了一定的负面影响,削弱了船舶抵抗风浪的能力,但本船仍具备重复的稳性安全冗余,能够满足现行法规中对于完整稳性的有关技术要求.
3 波浪引起横摇角敏感性分析
3.1 计算模型
3.1.1 经验公式计算横倾角
在COMPASS中计算横倾角的经验公式为:
(2)
式中:X1、X2、k以及s为系数,通过查表可知[2],r=0.73+0.6(KG-d)/d;其中d为船舶平均吃水,m;KG为货物重心,m.
由于COMPASS中计算波浪作用向上风一侧的横摇角是采用经验公式计算[15],对于不同的船型存在着不确定的误差,所以文中又采用WALCS软件,针对船舶在不规则波中的系泊状态时的横倾角进行精确计算,然后将计算所得的横倾角替换COMPASS软件计算所得的GZ曲线中的横倾角,在定义域范围内进行积分,计算GZ曲线下方的面积,根据公式算的衡准值k[16].
3.1.2 波浪诱发横摇的数值模拟
波浪对于横摇的诱发可以采用耐波性试验和数值模拟两种方法进行研究和评估,耐波性实验又主要包括静水实验、规则波试验、不规则波实验和瞬态实验[17].其中,不规则波模型试验主要通过船舶模型在不规则波中的运动响应试验,以确定船体在不同频率下的横摇角及运动加速度[18].文中采用水动力数值分析方法,基于经典势流理论,针对船舶在不规则波中系泊状态时的运动响应进行试验,从而确定在不规则波中的船舶横倾角变化曲线.不规则波模型试验能较真实地反映天然海浪作用下的船舶运动规律,船舶设计期间确定船舶耐波性的重要依据.
选取在COMPASS中计算所得,衡准值较小,即稳性状况较危险的8个工况进行横倾角计算,如表6.
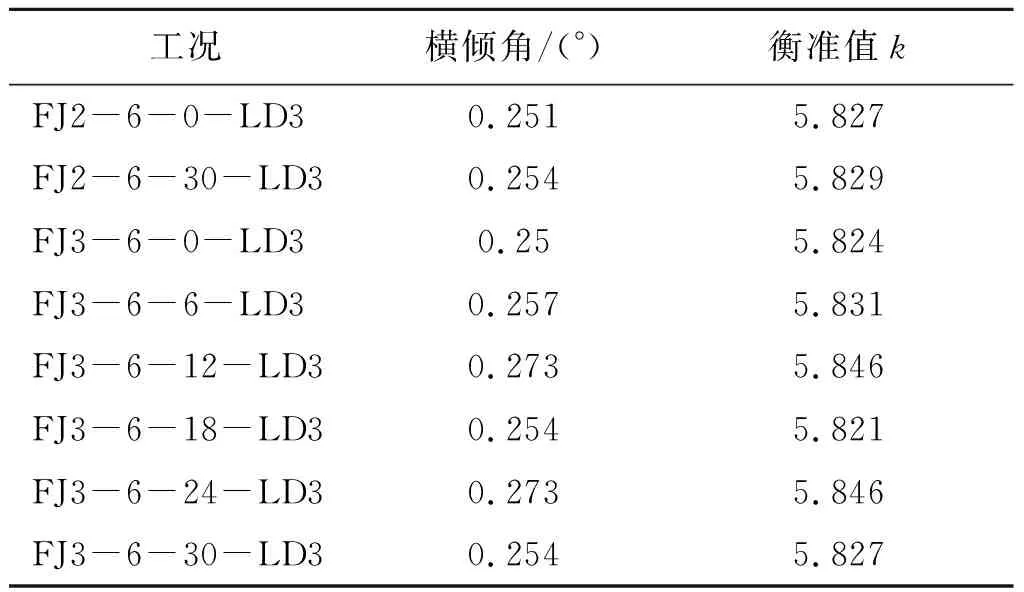
表6 COMPASS中计算结果
3.1.3 船体模型
首先从COMPASS中导出船体模型,在WALCS中建立船体模型,自动划分网格,如图3.

图3 WALCS中船体模型
然后设置根据设置的质量参数生成浮态网格,如图4.

图4 浮态网格
3.2 不同计算方法对比研究
利用建立好的船舶模型,在不规则波中进行耐波性计算,获得不同频率下的运动响应幅值,计算环境是无限水深,主要参数包括浪向角θB、入射角度等.其中入射波周期Ts设置为1.5~18.5 s,间隔1 s.有义波高Hs分别为9、11、12.5 m,浪向角设置为0~180°.在波浪条件下进行计算,得出不同参数下的横摇θR响应数据,如图5.
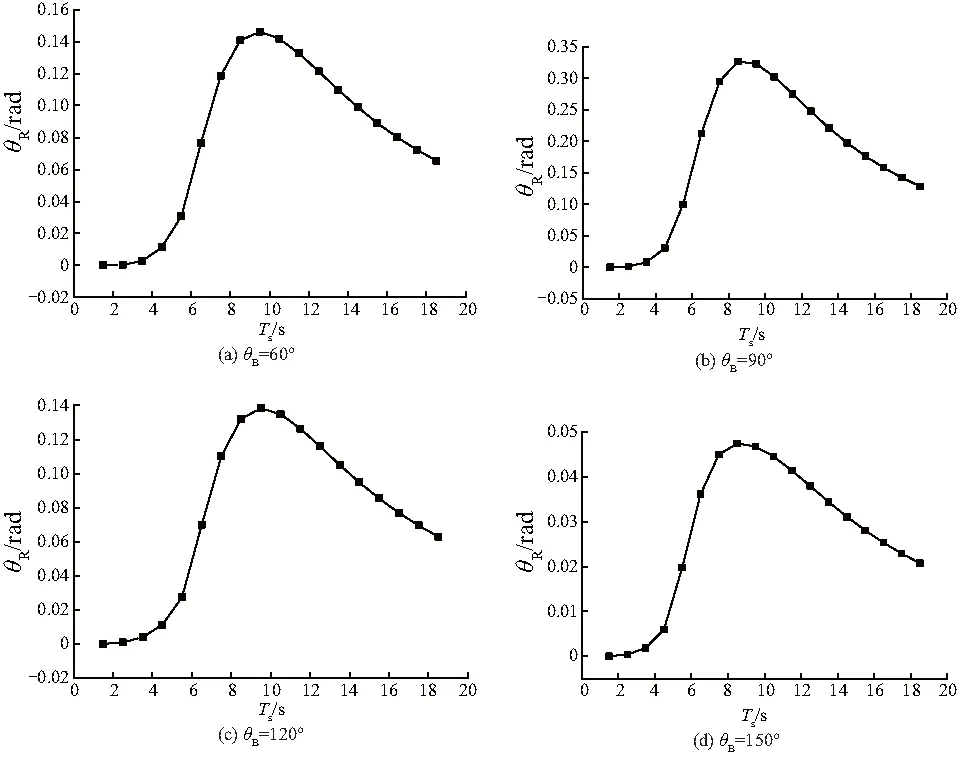
图5 有义波高12.5 m时不同浪向角下的横摇响应
根据上图,比较不同浪向角下横摇响应曲线的峰值点,将其作为最大初始横倾角进行稳性校核,其中当入射角达到90°时,此时的最大初始横摇角达到最大值0.326 rad,说明浪向角对于横摇角有较大影响,且达到垂直入射时,横摇角最大.
比较相同浪向角下,不同有义波高Hs对横摇角的影响,如图6.

图6 浪向角为90°时不同有义波高下的横摇响应
根据图6,比较不同有义波高下的横摇响应曲线的峰值点,发现有义波高越大,船舶模型的最大初始横摇角越大,由于COMPASS软件是在风速为26 m/s的情况下进行稳性计算,对照普氏风级表以及海况等级表,在该风速下的有义波高为9~12 m.所以选择在有义波高12.5 m时,浪向角为90°时计算所得的横摇角最大值,利用梯形积分法,按照公式计算气象衡准值k,并与COMPASS的计算结果进行比较,如表7.
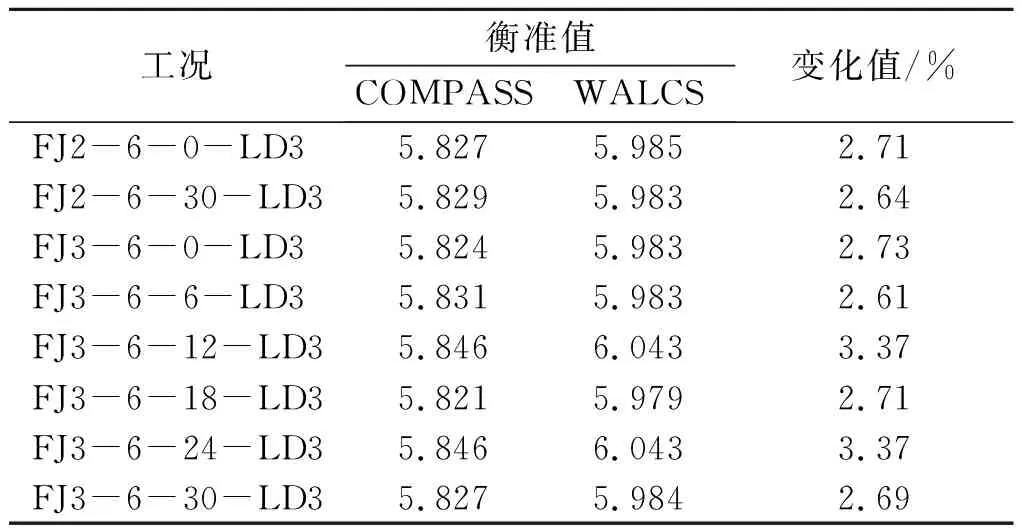
表7 两种计算方式衡准值的变化值
由表可以看出,COMPASS中经验公式计算得出的衡准值更加保守,在相同情况下,COMPASS校核的船在保证正常海况下安全行驶的同时,还能够适应更加恶劣的海况,其稳性裕度更充足,安全性更高.
4 结论
(1) 以风电设备对系泊状态下养殖工船稳性的影响为研究对象,借助COMPASS软件,在不同工况下的装载进行建模,针对不同风电设备的安装位置,在风电设备静止时对模型展开数值计算,发现安装风电设备前后,稳定风作下的横倾角增加了8.4%,其各项指标仍然满足完整稳性规则的有关要求.
(2) 当风电设备工作时,载荷总体上对于船舶的完整稳性有一定的负面影响.但根据上述计算假定施加的风电载荷后,船舶完整稳性会减小10%左右,说明风电载荷总体上对于本船的完整稳性有一定的负面影响,但船舶削弱后的稳性裕度仍能满足现有法规对于船舶完整稳性的有关技术要求.
(3) 通过WALCE进行大量计算,比较经验公式计算与文中直接计算方法所得到的波浪载荷横倾角结果,发现使用规范中的经验公式计算波浪载荷对船造成的横倾角会比直接计算法得到的结果小4%左右,说明经验公式更加保守,这样会使得完整稳性衡准值的富余量更加充足,设计的船舶更加安全.
