基于选择性高斯过程集成的天线谐振频率建模

张天亮，田雨波，陈学志，高 婧

(江苏科技大学 电子信息学院，镇江212100)

近年来，大数据的进步所带来的问题越来越难以解决，如果仅依靠单一的机器学习模型，已经很难达到很多复杂问题的要求.此时集成概念被创造性的提了出来，并吸引了很多的学者对其进行钻研.1990 年，文献[1]采用构造性方法实现了集成多个弱学习器可以得到更强的学习器的理论，证明了集成学习的优异性.1996年，文献[2]提出了Adaboost算法，实现了集成学习从理论到实际应用的跨越.同年，Bagging算法问世[3]，该算法通过自主采样法处理训练样本，得到若干数目相同但有一定相似度的训练子集，然后采用子集训练若干弱模型，最后将若干弱模型进行集成.2002年，文献[4]提出了“选择性集成”的概念，主要是对模型进行筛选，表现优异的模型则参与集成，从理论与实际方面均证明了该方法的有效性.2016年，文献[5]提出了一种基于Boosting的XGBoost方法，在某些方面其学习性能可以与深度学习比肩.

粒子群算法(particle swarm optimization，PSO)作为一种被广泛使用的算法，具有易实现、计算量小、参数少优点[6].高斯过程(Gaussian progress，GP)作为一种机器学习方法，这些年发展迅速[7]，相比于神经网络[8]、支持向量机回归[9]、径向基函数网络[10]等，具备如下两大特点：高斯过程在学习过程中参数不多，易实现；对解决一些样本数量小，维数比较低，非线性等复杂问题取得很好的效果[11].文中提出一种基于PSO的高斯过程集成方法，通过一组样本建立若干具有不同核函数的高斯过程模型，并根据粒子群优化算法，寻找一组最优权重，对所建立的若干高斯过程回归模型进行加权集成，得到最终模型，并且将最终模型用于微带天线谐振频率建模，与单一GP和神经网络等算法对比，精度明显提高.

1 高斯过程回归原理

高斯过程模型是一种非参数化模型，对于待测样本，能够进行预测并且给出预测方差，高斯过程可以均值函数和协方差函数唯一确定[12]，即

m(x)=E[f(x)]

(1)

K(x,x′)=E{[f(x)-m(x)][f(x′)-m(x′)]}

(2)

式中：x,x′∈Rd为随机变量,故GP也可以用如下公式表达：

f(x)～GP(m(x),k(x,x′))

(3)

若给定训练样本集为D={(Xi,yi)|i=1,2,…,n}，其中Xi=[x1,x2,…,xn]为d×n维的训练输入矩阵；yi=[y1,y2,…,yn]为相应的n个训练输出标量yi组成的训练输出矢量；y为训练样本的标签；f*为测试样本的标签，则y和f*的联合高斯分布为：

(4)

式中：X为训练输入样本；x*为测试输入样本.K(x*,x*)、K(X,x*)为n*×n*阶协方差矩阵.

高斯过程只需要训练一组超参数，这也是唯一需要确定的参数，并且该参数决定了高斯过程的性质，最优超参数一般情况下可以由最大似然法计算得到，先计算训练样本的条件概率，然后计算其对数似然函数L(θ)，再对其超参数求偏导，最后的优化算法采用共轭梯度算法[13].L(θ)和其偏导数如下：

(5)

(6)

式中：C为训练样本的协方差矩阵；θ为一组超参数.得到最优超参数以后，可以根据式(1，2)对测试集进行估计.

2 基于粒子群优化的选择性高斯过程集成

2.1 粒子群优化算法原理

粒子群算法[14]属于一种简化的社会模型，该方法是对鸟群捕食的行为规律进行模拟而提出的一种优化算法，其原理是使用一群一定数量的粒子，在目标区域内通过彼此间的协作和信息资源共享，在具体问题的可行解中搜索满足条件的解，并选择搜索范围之内最优的解作为最终的解.在粒子群算法中，粒子在寻优的过程当中，需要控制粒子的移动方向和快慢以及最优位置，分别用速度和位置表示.假设粒子的搜索空间是n维的，整个粒子群x=(x1,x2,…,xm)T中包含m个粒子.第i个粒子的位置在xi=(xi,1,xi,2,…,xi,n)T处，此时粒子的速度为vi=(vi,1,vi,2,…,vi,n)T，粒子的个体极值为pi=(pi,1,pi,2,…,pi,n)T.当粒子找到局部最优位置pbest和全局最优位置gbest之后,可以更新自身的速度和位置.粒子之间除了时刻更新自己的位置之外，在迭代寻优的空间中用一个相关的适应度函数来衡量一个粒子位置的好坏以及控制算法在寻优过程中粒子的运动基准.

每个粒子在迭代寻优过程中不同时刻的速度和位置更新表示为：

(7)

(8)

式中:ω为粒子的惯性权重，主要作用是提高粒子的搜索能力,恰当的ω值使得粒子具有均衡的广域搜索能力(exploration)和局部搜索能力(exploitation)；c1、c2为学习因子，一般为正常数,起到了控制粒子的寻优路劲的效果，也影响了粒子速度的更新；λ1、λ2为均匀随机数，取值范围为[0,1].

2.2 基于PSO选择性高斯过程集成

为了提高高斯过程模型对测试样本的预测能力，采用粒子群优化算法根据模型的训练误差，得到一组最优集成权重.假设已经分别训练出k个核函数不一样的高斯过程模型{f1,f2,…,fk}，粒子群算法的主要作用是通过若干粒子寻找到一组最优的集成权重{ω1,ω2,…,ωk}，且粒子的空间维数等于高斯过程的个数k.设原始样本集为D={(x1,y1),(x2,y2),…,(xN,yN)},其中N为样本个数，从中选择n组数据作为训练样本，剩余s组用来测试.文中提出的集成流程如图1，算法具体步骤如下：

步骤一： 选择k个具有不同核函数的高斯过程，用n组训练数据分别对这k个高斯过程进行训练，可得到k个核函数不一样的高斯过程模型{f1,f2,…,fk}.

步骤二： 根据已建立的高斯过程模型，可得到训练集误差.训练误差选择平均相对误差(mean relative error, MRE)作为评估指标，定义如下：

(9)

式中：f(xi)为高斯过程的预测值；y(xi)为真实值；n为样本数量.

步骤三：将步骤二中得到的训练误差作为粒子群算法的适应度函数，利用粒子群算法寻找这k个模型的最优集成权重{ω1,ω2,…,ωk}.

步骤四：根据得到的最优权重，将上述k个模型进行加权集成，得到最终模型为：

(10)

式中：ωi为模型融合的权重.

步骤五：验证阶段使用s组测试样本对最终得到的集成模型精度进行测试；同时使用测试样本对每个单一高斯过程模型的精度进行测试，选择MRE作为测试误差评估指标，进行集成模型与单一模型的精度对比.

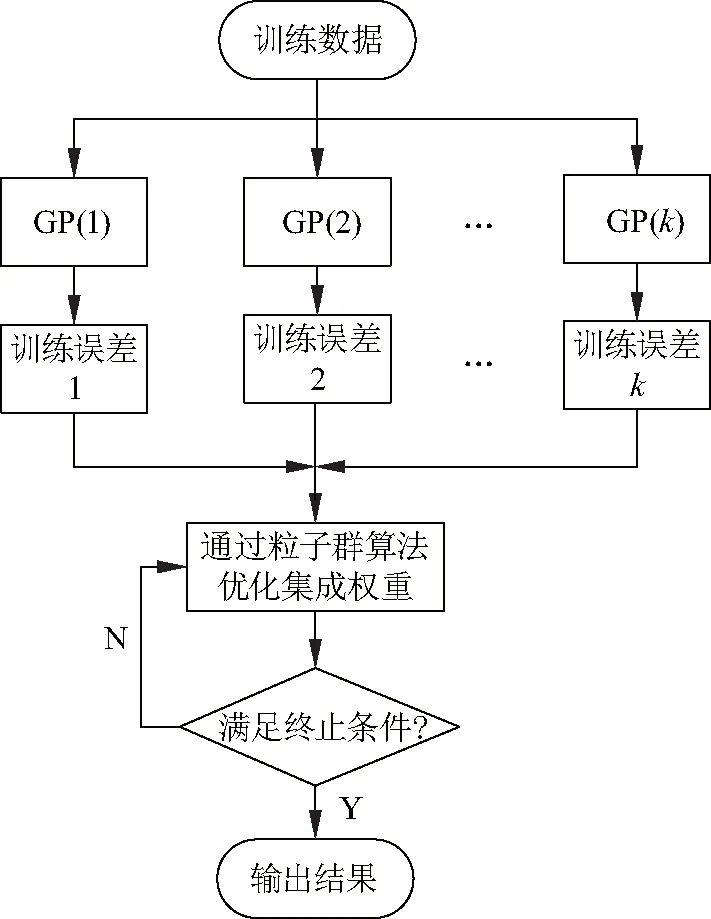
图1 基于粒子群优化的选择性高斯过程集成流程

3 圆形微带天线谐振频率建模应用

微带天线(microstrip antennas, MSA)是由导体薄片粘贴在背面有导体接地板的介质基片上构成的天线，它具有剖面薄、体积小、重量轻、价格低廉等优点，目前用于宽广频域上，频率范围大约为100 MHz～100 GHz[15].微带天线的贴片可以设计为不同的形状，如蝶形、扇形、星形等，文中采用如图2圆形微带天线谐振频率进行建模，其TM11模式下谐振频率为[11]：

(11)

式中：K11=0.293；f11为天线的谐振频率；c的值为3×108m/s；εr为相对介电常数.

若考虑边缘效应，式中的半径a可用如下经验公式计算的等效半径ae代替

(12)

式中：h为介质层的厚度.圆形微带天线的谐振频率主要取决于h,εr以及圆形微带天线贴片的几何尺寸a.

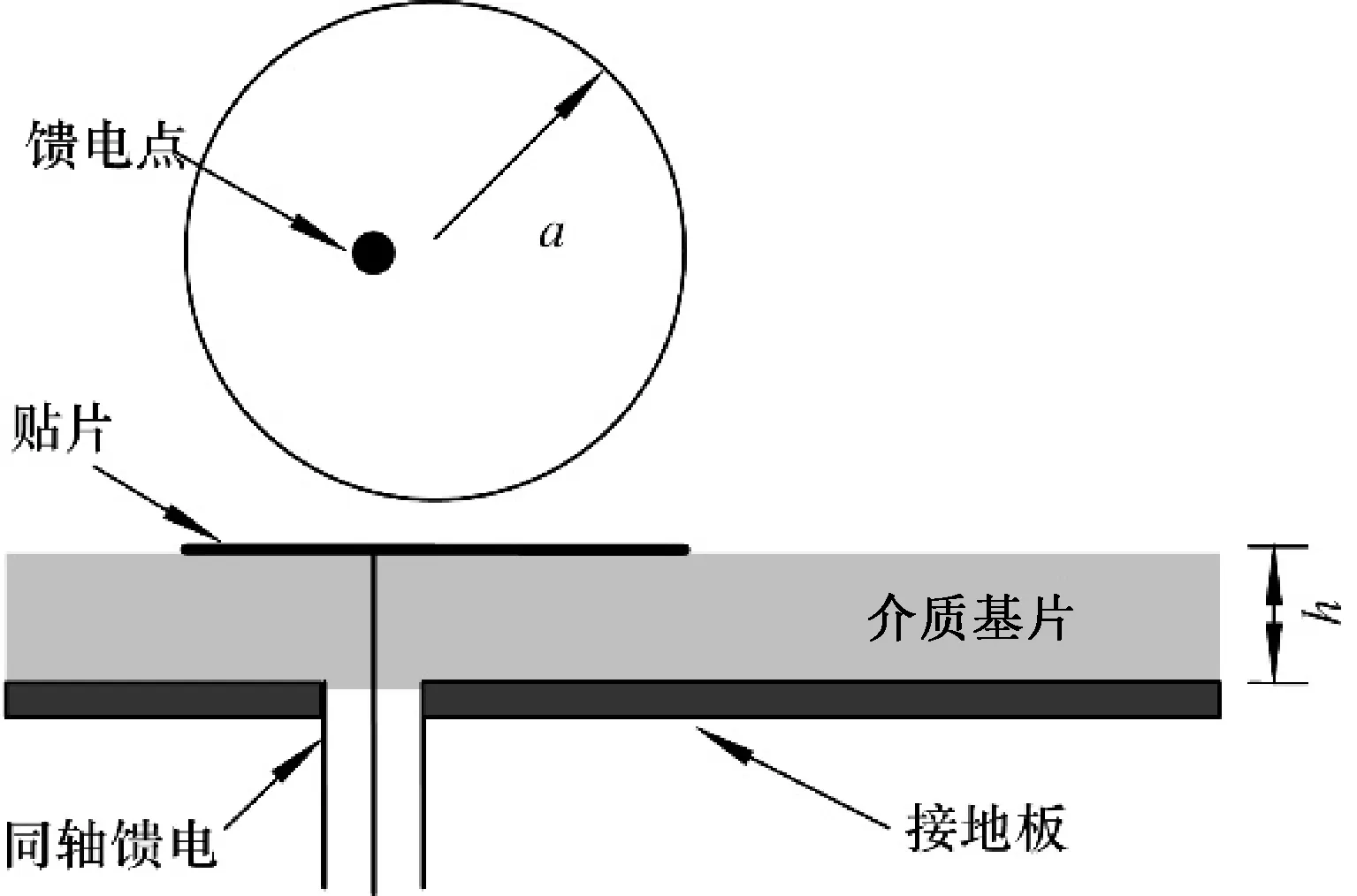
图2 圆形微带天线模型

文中以参数h，εr和a作为输入，谐振频率f11(MHz)作为输出，选择20组数据[16-21]进行建模，如表1，其中2～4列给出了圆形微带天线的相关数据，第5列为测量得到的真实谐振频率数值，共有20组数据，其中16组用于训练，4组用于测试(带有*标注)，模型分别选择以RBF、Matern32、Matern52、ARDMatern32、ARDMatern52为核函数的5个高斯过程模型.表1中第6列为使用文中方法得到的结果，第7～8列为文献[22]提出的神经网络模型得到的结果，其中fDBD、fBP分别代表使用启发式算法(Delta-bar-delta，DBD)和反向传播算法(back propagation, BP)的神经网络模型得到的频率.表1中最后一行列出了每种方法实测值与预测值之间的误差总和，可以看到，文中模型计算得到的数据比上述文献计算得到的更接近与真实值，说明文中精度更好；表2为文中模型与单一高斯过程模型效果的比较，结果表明使用文中模型的效果要优于单一的模型.

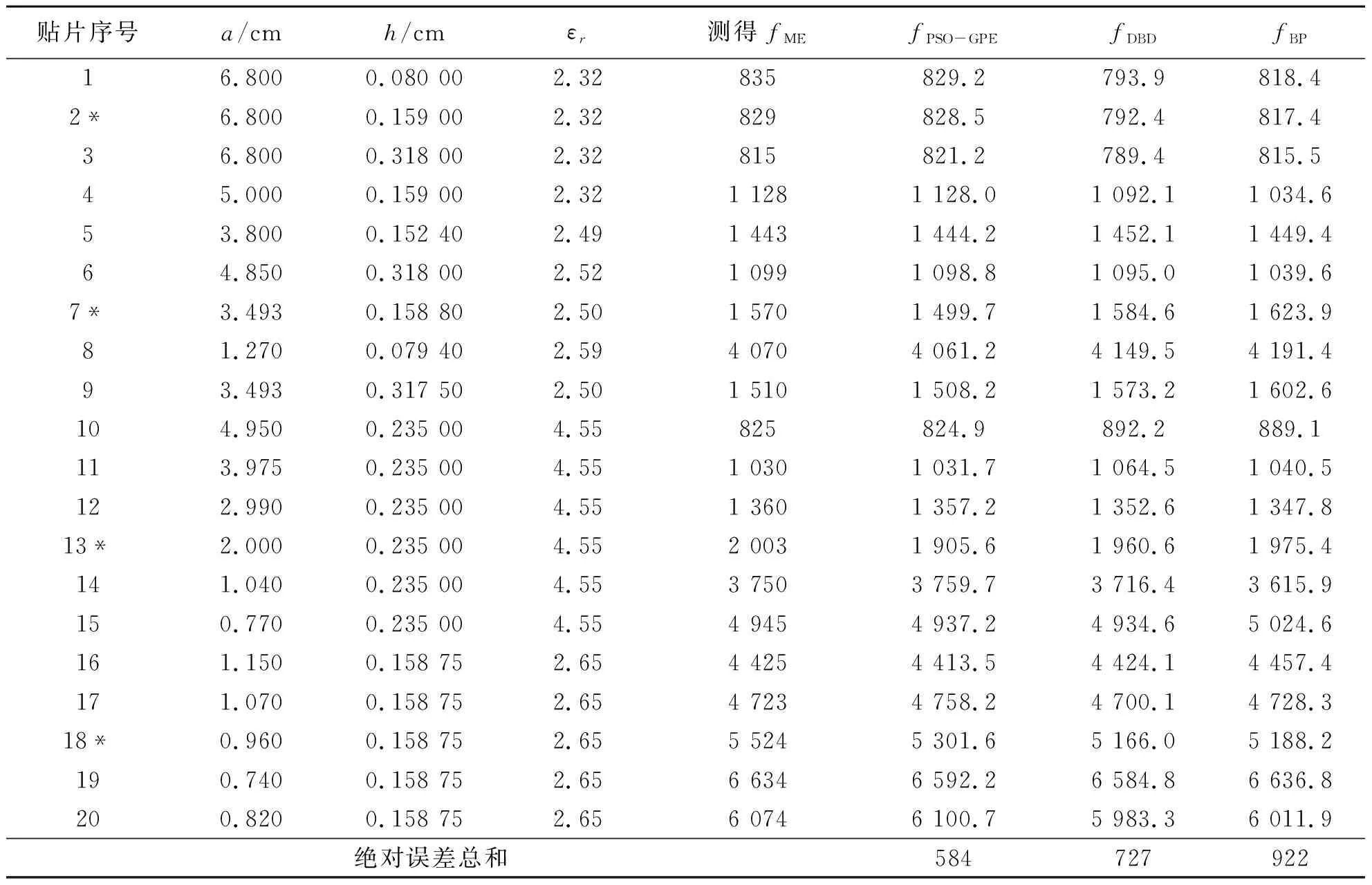
表1 圆形微带天线TM11模式下的谐振频率

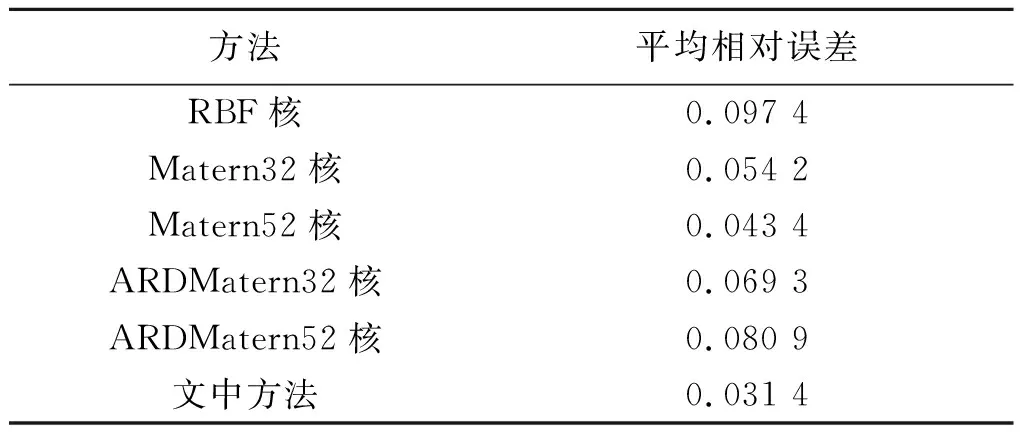
表2 圆形微带天线仿真结果对比

4 结论

文中提出了一种基于粒子群优化的高斯过程集成算法，根据单个模型的训练误差，利用粒子群算法强大的全局搜索能力寻找到最优的一组集成权重，然后根据该权重对若干具有不同核函数的高斯过程进行集成，得到精度和泛化能力更优的学习器.同时，通过圆形微带天线谐振频率实验：与已有文献的结果对比，使用文中方法得到的结果更接近真实值；并且通过与单一高斯过程做比较，结果表明使用文中模型的效果更好.