考虑电网结构和参数的电力系统惯量分布特性

2021-12-12刘方蕾胥国毅刘家豪毕天姝郭小龙

电力系统自动化 2021年23期

刘方蕾，胥国毅，刘家豪，王程，毕天姝，郭小龙

（1. 新能源电力系统国家重点实验室（华北电力大学）,北京市 102206；2. 国网上海市电力公司青浦供电公司,上海市 201700）

0 引言

电力系统惯量是衡量系统频率稳定的重要参数之一。随着风电、光伏等新能源大量接入,系统等效惯性时间常数不断下降,扰动事件下频率变化程度增加［1］。近年来,中国“9·19”锦苏直流事故及英国电网“8·9”事故等引发了学者对系统惯量问题的关注［2-3］。随着新能源占比不断增加,系统中惯量分布不均的现象更加突出,扰动发生后频率响应时空分布特性也日益明显［4］。因此,研究电力系统惯量分布特性对系统的频率稳定分析与控制具有重要意义。

国内外专家对电力系统惯量分布开展了大量研究,主要可分为两个方面：①系统中机组或区域等效惯量估计；②系统中不同节点惯量相对大小的研究分析。针对内容①,文献［5］基于自回归移动平均模型辨识技术,对系统中同步机组惯性时间常数进行辨识。文献［6］根据机组频率响应相似程度进行分区,通过区域间联络线功率变化和系统频率,基于转子运动方程对区域惯量进行评估。文献［7］采用参数辨识方法,通过实时运行稳态功率与频率数据估计系统等效惯量。上述文献中的惯量量化评估将系统或区域视作惯量相同,未细化不同节点的惯量分布特性。

随着系统中大型机组投运和新能源大量接入,系统惯量水平分布不均的特征更加明显。文献［8］通过欧洲电网扰动数据分析表明：在区域等效惯量满足要求的情况下,由于大规模新能源接入,区内惯量差异极其明显,频率响应差异显著。文献［9-10］考虑频率时空分布特性,对节点频率特性进行了量化分析,提出了惯量量度指标来反映不同节点的频率特性差异。文献［11］利用仿真分析了系统整体惯量不变而分布不同时的频率响应,结果表明惯量分布会对系统频率特性造成显著影响。文献［12］通过对两机系统惯性中心的推导,分析了两侧机组惯量分布对系统惯性中心和频率特性的影响。文献［13］从频率和惯量的关系出发,定义节点惯量为节点频率与惯性中心频率的偏差相对大小,为一个定性指标。文献［14］定义节点惯量为扰动后某一时刻发电机端功率不平衡量与节点频率变化率的比值,所得节点惯量矩阵随扰动、时间变化,难以反映系统惯量这一固有特性。文献［15-16］从系统中扰动以机电波规律传播的角度出发,利用同步相量测量单元（PMU）采集扰动数据,计算不同节点的扰动传播速度来衡量不同区域惯量水平高低,上述文献仍是对惯量水平的相对分析。

综上所述,目前关于电力系统惯量的研究集中在区域或整体惯量数值的评估及定性衡量各节点惯量的相对大小,缺乏对系统中不同节点惯量分布特性的定量描述。因此,本文定义了节点的计算惯量指标,用以表征不同节点发生扰动后对频率变化的阻碍能力,对两机和多机系统的计算惯量进行了推导,得到节点计算惯量表达式。在此基础上,基于灵敏度分析研究了不同区域间惯量的相互影响。

1 节点计算惯量

1.1 节点计算惯量定义

电力系统中,发电机转子作为一个旋转刚体,具有转动惯量,当出现功率不平衡时,发电机会释放旋转动能来平衡功率差额。发电机的惯量常用惯性时间常数H来表示,新能源机组输出功率与系统频率解耦,无法提供惯量,系统等效惯性时间常数Hsys由发电机惯量聚合得到［17］,即

式中：p和q分别表示同步发电机和新能源机组的数量；Sj和Si分别表示同步发电机j和新能源机组i的容量；Hj为同步发电机j的惯性时间常数。

系统发生功率扰动时,扰动功率大小、惯性时间常数、频率之间的关系如下。

式中：fcoi和ΔPsys分别为系统惯性中心频率和功率不平衡量。

系统等效惯性时间常数描述的是系统整体对于频率变化的阻碍能力,是基于系统惯量均一的假设。实际上不同节点发生功率扰动时,系统的频率响应（初始频率变化率）不同,频率变化率常作为系统保护与控制装置的触发信号［18］,许多国家对频率变化率限值提出了要求［19-20］。考虑系统发生功率扰动后频率变化最为剧烈的初始时间段,参照系统等效惯量与系统功率和频率变化的关系,定义节点k的计算惯量为节点k处发生功率扰动后,扰动功率大小与节点k处初始频率变化率的比值,即

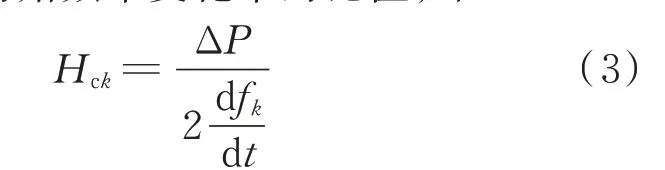
式中：Hck为节点k的计算惯量,其在数值上相当于节点k处一台虚拟的同步发电机所具有的惯性时间常数,如图1 所示；ΔP为节点k处扰动功率；fk为节点k处频率。

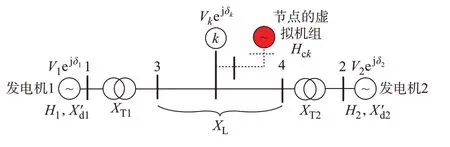
图1 两机系统结构示意图Fig.1 Schematic diagram of structure of two-machine system

需要注意的是,节点本身不具备惯量,计算惯量是系统惯量在节点处的体现,其大小表征了该节点初始频率响应特性,研究不同节点的计算惯量可以对系统的惯量分布特性进行描述。

1.2 两机系统节点计算惯量

如图1 所示,两侧发电机惯量分别为H1和H2,发电机内电势电压幅值、相角分别为V1、δ1和V2、δ2,节点k为两机之间任意一点,其电压幅值和相角分别为Vk和δk,两侧发电机的暂态电抗、变压器电抗分别为X′d1、X′d2和XT1、XT2,线路阻抗为XL。

定义α为节点k到发电机1 的距离,有

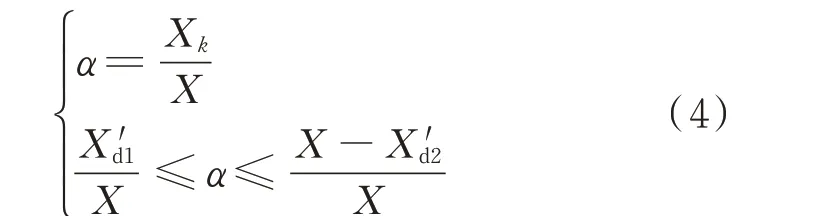
式中：Xk为节点k到发电机1 内电势的阻抗；X为两侧机组之间的总阻抗,X=X′d1+XT1+XL+XT2+X′d2。

节点k的电压可由两侧发电机内电势表示,即

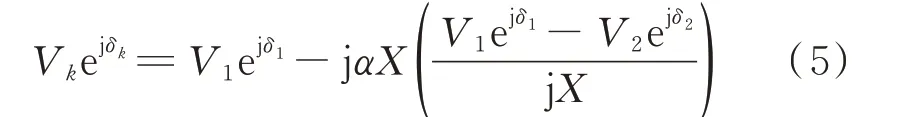
由式（5）可得节点k的电压幅值为：

以标幺值的形式来表示,则节点k的频率可以由发电机1 和2 的频率得到,即

式中：f1和f2分别为发电机1 和2 的频率。

若节点k处出现功率扰动,忽略负荷的功频特性,不平衡功率按同步功率系数分配到各同步发电机,同步功率系数为［21］：

式中：Djk为发电机j节点k处的同步功率系数；Vj为发电机j的内电势幅值；Bjk为收缩到发电机j内电势节点和故障节点k的电纳；δjk0为发电机j和节点k间电压的初始相角差。新能源机组不具备同步发电机组的转子运动特性和电磁暂态特性,在扰动发生瞬间,无法分担系统不平衡功率。

节点k处发生ΔP的功率扰动后,两侧发电机不平衡功率分别为：

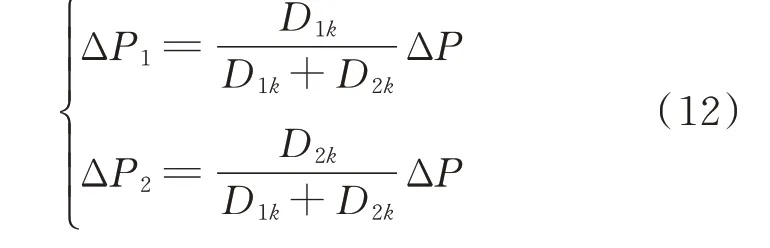
式中：D1k、D2k和ΔP1、ΔP2分别为两侧发电机对应的同步功率系数和拾取的不平衡功率。

因此,可得发电机机端频率变化率为：

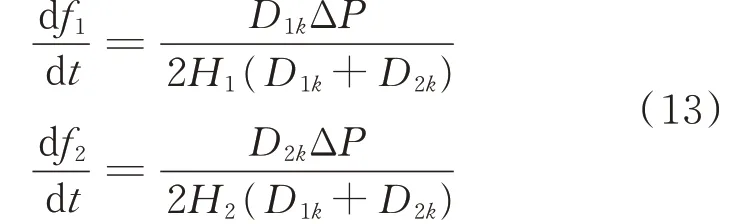
将式（10）和式（13）代入节点的计算惯量定义式（3）,可得节点k的计算惯量为：

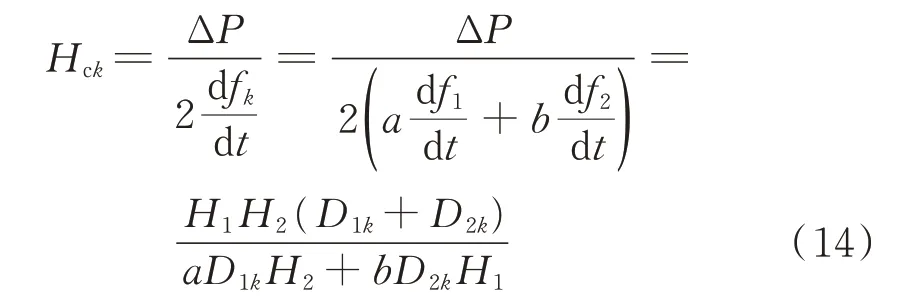
由式（14）可以看出,节点的计算惯量主要与发电机惯量H1、H2以及a、b、D1k、D2k等系数有关,而a、b、D1k、D2k等系数又主要取决于系统参数和节点k的位置。因此,当系统参数确定的情况下,节点的计算惯量主要与其所处的位置以及两侧系统的惯量有关。

1.3 多机系统节点计算惯量

多机系统示意图如附录A 所示,系统中共有n+m个网络节点,其中n为发电机端节点个数,m为其他节点个数。以此系统为例,推导系统中任意节点k的计算惯量。

忽略电导影响,计及发电机暂态电抗并将负荷简化为等值导纳后得到系统增广导纳矩阵［22］,即

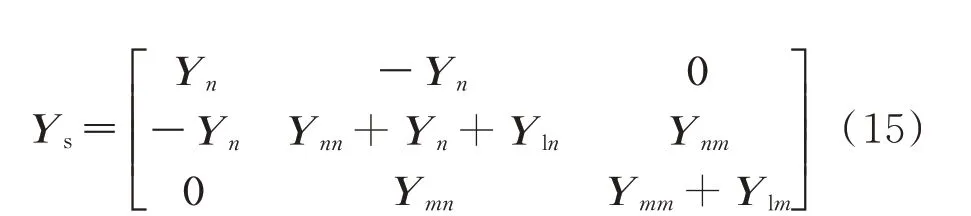
式中：Ys为系统的增广矩阵；Ynn和Ymm分别为发电机节点和其他节点的自导纳；Ynm和Ymn分别为发电机节点和其他节点的互导纳；Yn为发电机暂态电抗构成的对角阵；Yln和Ylm分别为发电机节点和其他节点处的负荷等值导纳,这里均只考虑电纳部分。

对应的网络方程为：

根据上述网络方程,将网络节点的电压用发电机节点电压表示,即

式中：R表示网络节点电压与发电机内电势节点电压之间的关联矩阵,R=−Y−14Y3,取决于系统的导纳矩阵。

提取式（17）中与节点k相关的部分,在节点k处发生故障后,故障点电压可由各发电机内电势表示,即

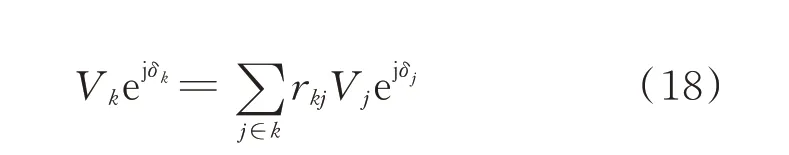
式中：δj为发电机j的内电势对应的相角；rkj为矩阵R中表示节点k和发电机j电压关系的元素；j∈k表示取R中节点k所在行对应的元素。

将式（18）表示的节点k的电压进行变形和简化,如式（19）所示,最终得到节点k的电压角度如式（20）所示。需要说明的是,在多机系统中,不同节点相角可能差异较大,式（19）中的第4 行式子可能存在一定误差,但由于联系较远的两个节点间对应的关联矩阵元素rkj较小,使得这一简化导致的误差减小。

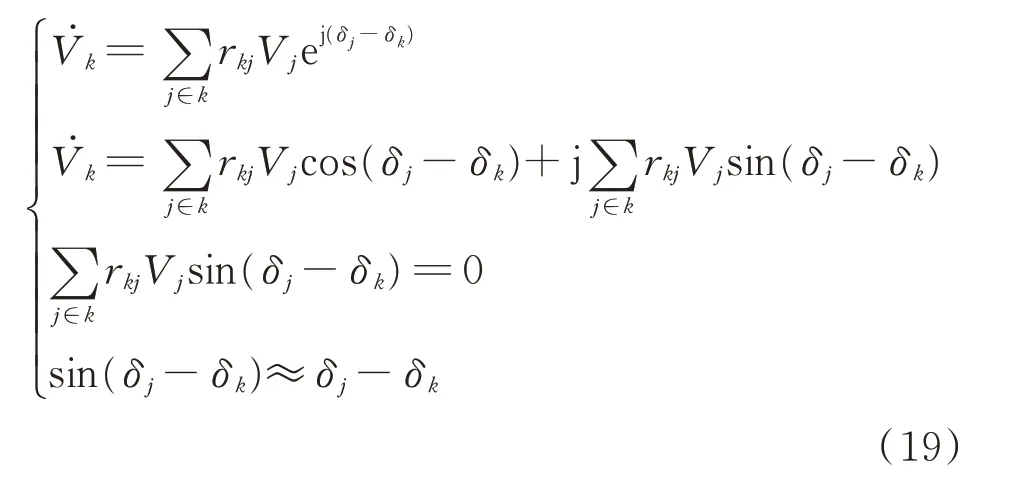
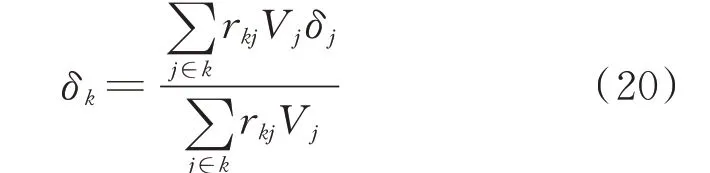
由式（20）得到节点k的频率如式（21）所示,即实现利用同步机频率表示网络节点的频率。

式中：fj为发电机j的频率。

节点k处出现扰动功率ΔP时,不平衡功率基于式（11）所示同步功率系数被分配到各发电机节点处,发电机j拾取的不平衡功率为：

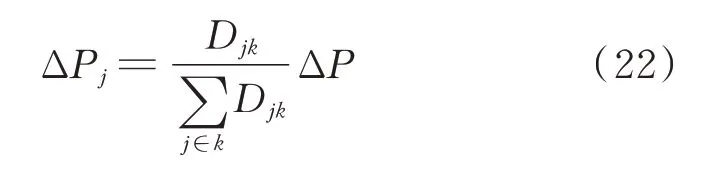
式中：Djk和ΔPj分别为发电机j对应的同步功率系数和拾取的不平衡功率。

由发电机转子运动方程和式（22）,得到发电机j的频率变化率为：

将式（21）和式（23）代入式（3）,主要计及电纳影响,考虑系统电压在额定值附近,最终得到节点k的计算惯量为：

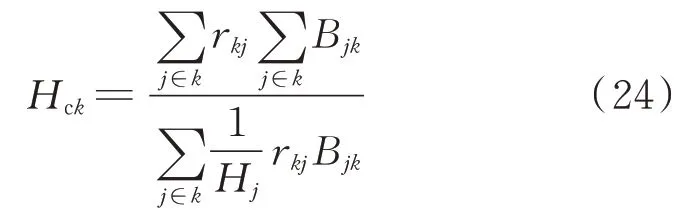
可以看到,对于多机系统来说,影响节点计算惯量的主要因素为各发电机的惯量大小和节点到发电机的电气距离。

1.4 节点计算惯量灵敏度分析

根据电气距离以及惯量的分布特征不同,节点计算惯量受不同区域惯量大小的影响也不相同。变量之间的影响程度常用灵敏度来表示,因此可以对计算惯量进行灵敏度分析,来衡量区域内节点的频率响应特性受本区域和其他区域惯量的影响。

基于两机系统分析,将图1 所示两机系统划分为两个区域：区域1 和区域2,如附录B 所示,选取区域1 内部节点3,分析其计算惯量受H1和H2的影响程度。区域1 内部发电机暂态电抗与变压器电抗之和表示为X1（X1=X′d1+XT1）,发电机2 的惯量H2与节点3 之间的电抗表示为X2（X2=X′d2+XT2+XL）。用d=X2/X1来表示两区域间的距离,当两侧区域间距离增大时,d增大。

忽略运行点的影响,考虑各节点电压角度差很小,系统电压在额定值附近,基于式（14）求解节点3的计算惯量Hc3对于H1和H2的灵敏度,结果如下。

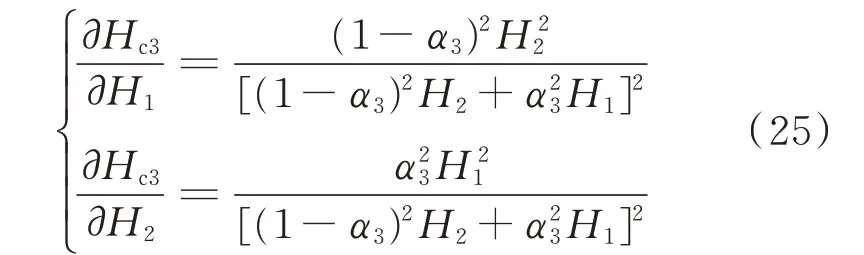
式中：α3为节点3 到H1的距离,其与两区域间距离d的关系如下。

由式（25）所示的Hc3对两侧系统惯量的灵敏度表达式可以看到,当两区域间的距离增大时,Hc3对区域2 的惯量H2的灵敏度减小,说明此时节点3 处初始频率响应特性受H2的影响减小。

对于多机系统,由式（24）求取任意节点k的计算惯量Hck对发电机j惯量的灵敏度,结果如下。

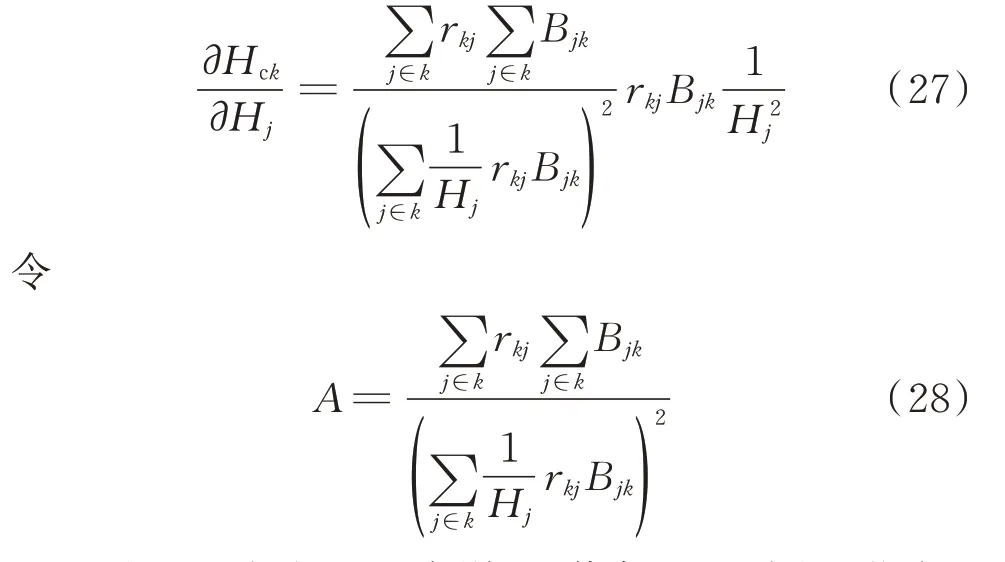
对于所有发电机来说,A值都是一致的,节点k的计算惯量Hck对发电机j惯量的灵敏度主要取决于系数rkj Bjk和其惯量Hj。系数rkj Bjk由节点k与发电机j之间的电气距离决定,距离越远,该系数的值越小。在发电机惯量一定的情况下,Hck对Hj的灵敏度越小,也就说明受Hj的影响越小。

2 仿真算例

2.1 计算惯量的验证与结果分析

基于图1 所示两机系统,对比理论推导结果（式（14））和暂态仿真计算得到的节点计算惯量来进行验证。在PSASP 软件中建立对应的系统模型,通过在各节点设置扰动,根据扰动大小和初始频率变化率求出计算惯量,为了避免初始暂态过程及单个测量点偶然误差的影响,取扰动发生后0.2 s 内的平均频率变化率作为初始频率变化率。

设置系统基准容量均为100 MW,系统参数如附录C 表C1 所示,取联络线上任意节点进行验证,图2 所示为其对应的结果,其中实线为理论推导结果,星号为暂态仿真结果。

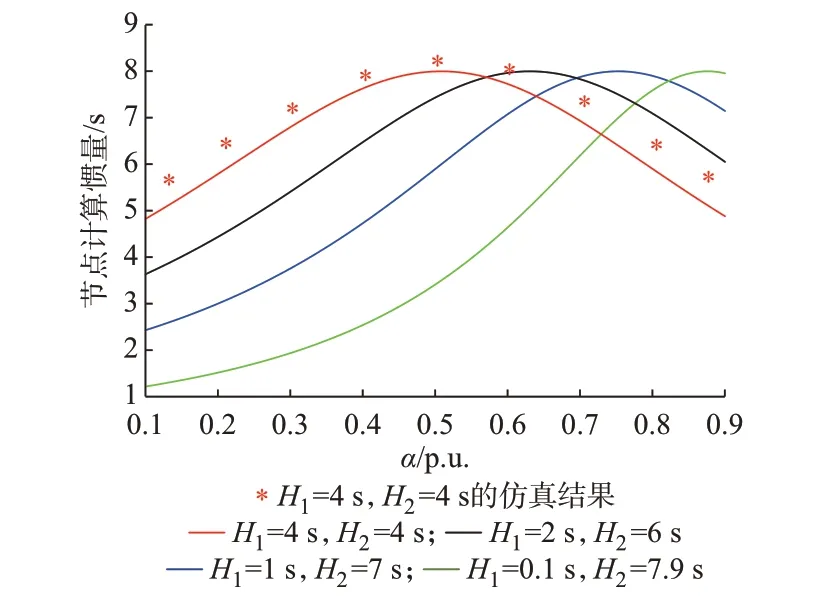
图2 两机系统节点计算惯量分布Fig.2 Distribution of calculated node inertia in twomachine system

从验证结果可以看到,理论推导与仿真结果相符,可以验证计算惯量的正确性。由于推导过程中忽略运行点的影响以及测量误差的存在,两者存在一定误差,但误差较小。

考虑惯量不同分布对节点计算惯量的影响,保持发电机总惯量为8 s,即H1+H2=8 s,分析在两侧发电机惯量不同的情况下的节点计算惯量,同样以联络线上节点的计算惯量为例进行分析,结果在图2 中绘出,图2 中不同颜色实线分别代表不同惯量分布情况下的结果。从图中可以看到,两侧惯量均匀分布时,系统整体计算惯量高于非均匀分布情况,如H1=4 s,H2=4 s 时系统中节点计算惯量明显高于惯量分布极度不均匀的情况,说明了惯量均匀分布有利于提高系统整体频率抗扰能力。文献［12］推导了两机系统惯性中心,本文得到的节点计算惯量最大点位于系统惯性中心,也进一步证明了利用节点计算惯量这一物理量来表征系统惯量特性的合理性。

为进一步说明系统中的惯量分布特性及新能源接入对系统计算惯量的影响,本文对8 机36 节点系统进行分析［23］,系统示意图如附录D 所示,发电机惯性时间常数和容量如附录C 表C2 所示,表C2 中发电机惯性时间常数均以其额定容量为基准值。求取系统各节点计算惯量,采用三次样条插值法得到整个系统的计算惯量,绘制出初始情况下系统不同位置的计算惯量热力图如图3（a）所示,在这里计算惯量以系统总容量为基准值来表示。

图3 多机系统节点计算惯量分布Fig.3 Distribution of calculated node inertia for multimachine system

从图3 中可以看出系统中不同位置的惯量分布情况,发电机G1 惯量大,其附近区域计算惯量大,发电机G6 惯量相对较小,其附近节点的计算惯量较小。为进一步说明多机系统惯量推导结果的正确性,对比分析了8 机系统中节点计算惯量的理论推导与仿真结果,如附录C 表C3 所示,本文只选取了误差最大和误差最小的5 个节点列出。可以看到,两者之间的误差较小,证明理论推导的正确性。

发电机G8 处以相同容量的风力发电机组代替其中一台常规机组,该区域惯量降低,得到风电接入情况下计算惯量热力图如图3（b）所示。从图中可以看到,当系统中同步机组被取代时,其附近区域的计算惯量水平降低,因此可以说明,当新能源机组取代同步发电机时,系统的惯量水平下降,频率稳定性降低。系统的计算惯量分布可以更加细致地衡量系统中各节点在发生扰动后初始时间段内对于频率变化的阻碍能力,从而识别惯量薄弱环节,为系统的频率控制提供参考。例如,让新能源机组提供虚拟惯量,降低薄弱点扰动后的初始频率变化率,提高系统整体的频率稳定性。计算惯量可以为细化系统的频率响应分析提供基础。

2.2 区域间惯量影响分析

本节基于式（25）所示的灵敏度分析来研究区域间惯量的相互影响。改变两侧区域间距离,在两侧惯量不同分布的情况下得到节点3 的计算惯量Hc3对于两侧惯量H1、H2的灵敏度,如图4 所示。

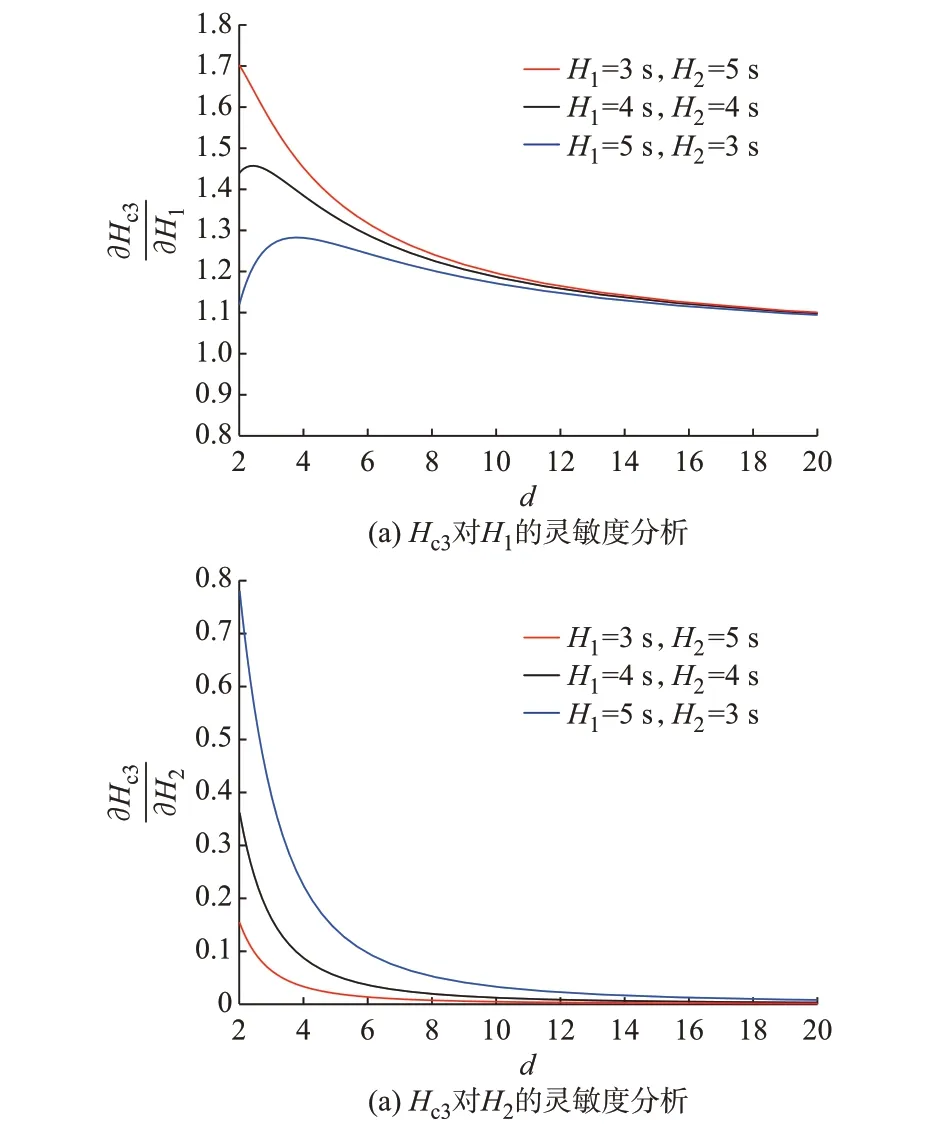
图4 Hc3对两侧惯量的灵敏度分析结果Fig.4 Sensitivity analysis results of Hc3 to H1 and H2

由图4 可以看到,当两侧电气距离改变时,节点3 的计算惯量Hc3对本侧惯量H1的灵敏度均较高,说明节点3 的初始频率响应特性受H1的影响较大。随着距离增大,节点3 的计算惯量Hc3对H2的灵敏度迅速减小,说明此时Hc3受H2的影响减小。通过图4中Hc3在不同惯量分布情况下对H2的灵敏度可以知到,两侧惯量的均匀分布程度也会改变区域间惯量的影响程度,在两侧惯量均匀分布的情况下,当距离d达到3.5 时,Hc3对H2的灵敏度降低到10%,说明此时H2的变化对区域1 内部节点3 的初始频率响应特性影响较小,在进行系统频率控制以提高系统的频率稳定性时,可优先提高区域1 内部的惯量。

进一步分析多机系统中区域间惯量影响,文献［24］将系统分为4 个区域,各区域包含机组情况如下。区域1：发电机G1、G2、G3、G5。区域2：发电机G4。区域3：发电机G6。区域4：发电机G7 和G8。取区域1 中的节点23 进行分析,分别设置区域1 中机组G1,区域2 中机组G4,区域4 中机组G7 的机组惯量发生变化,在PSASP 中仿真分析各区域惯量变化量ΔH对节点23 计算惯量Hc23的影响,结果如图5所示。

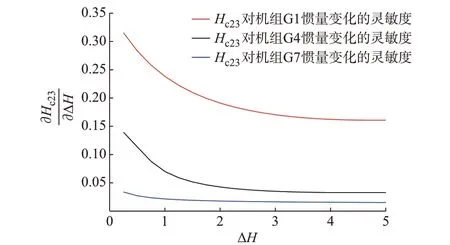
图5 8 机系统灵敏度分析Fig.5 Sensitivity analysis of eight-machine system

由仿真结果可以看到,当发电机G1 的惯量发生变化时,节点23 的计算惯量的变化较大,说明节点23 的计算惯量对区域1（G1）的灵敏度更高,而当发电机G4 或发电机G7 的惯量发生变化时,节点23的计算惯量的变化相对较小,节点23 的计算惯量对其灵敏度更低。仿真分析说明了在多机系统中,同样存在与两机系统类似结论。

从上述分析可以看到,增加本区域的惯量或者增加距离相近的区域惯量,对区域内的节点计算惯量影响更大,也就是说对于区域内节点阻碍频率变化的能力提高更多。因此,可以在系统中可能出现大功率扰动的区域及附近配置更多的惯量,如新能源虚拟惯量控制,以减少扰动初期频率变化率,提高系统频率稳定能力。