考虑风电-光伏功率相关性的因子分析-极限学习机聚合方法

叶 林，马明顺，靳晶新，李 卓，李镓辰，周天浦

（中国农业大学信息与电气工程学院,北京市 100083）

0 引言

中国“十三五”规划和相关政策的推进,使得风能、太阳能等清洁能源在近些年得到了快速发展［1］。由于高比例风电、光伏等不确定性电源［2］接入电网增加了规划和调度的复杂度,对电力系统的安全稳定运行带来了一定的冲击,因此需要对大量风电场、光伏电站进行建模仿真计算［3］,但这需要占用大量的时间和计算资源。所以,需要对大量风电和光伏场景进行削减或聚类［4］,降低电力系统仿真的计算时间和复杂度。

目前,对风电和光伏时序数据的聚合方法研究有许多,文献［5］针对风电功率聚合,提出了Kmeans-马尔可夫链蒙特卡洛（MCMC）聚合算法,但是K-means 算法的聚类中心是随机选定的,容易陷入局部最优；文献［6］针对K-means 聚类中心不稳定问题,采用枚举法和相关统计指标组合方法,得到光伏电站的典型运行场景集；文献［7］针对光伏功率聚合,根据瓦瑟斯坦距离对K-mediods 聚类加以改进,得到较好的光伏典型场景集；文献［8］基于近邻传播（AP）聚类与MCMC 方法的风电功率聚合方法,考虑了极端场景,并生成最佳聚类数；文献［9-10］对光伏功率序列的聚合考虑了天气类型的划分,并结合层次聚类和密度峰值聚类对天气类型进一步聚类。文献［5-10］有一个共同的缺点：仅考虑单个风电场或光伏电站的聚合,聚合得到的风电-光伏日场景单独归类,使得风电-光伏日场景间的对应次序发生混乱,改变了风电-光伏功率聚合序列相关性,影响了电力系统运行仿真计算。

考虑风电-光伏功率相关性的风电场、光伏电站的仿真建模已有大量研究,文献［11］基于5 种Copula 函数,通过欧氏距离检讨法建立的多风电场出力联合分布最优模型将光伏电场出力根据概率叠加生成了海量场景。该方法数据量过大,数据精度不高,导致系统仿真结果误差较大。文献［12］对风速和光照进行建模,采用阿基米德3 类Copula 函数分别构建相应的二元联合分布函数。然后,基于平方欧氏距离选择最优的Copula 函数,但其研究对象为风速、光照间的相关性,并不能完全代表风电-光伏功率时序特性。文献［13］基于风电-光伏出力数据构建了动态Copula 模型,但此方法将大量风电-光伏特殊场景与极端场景纳入考虑,导致模型复杂度高、求解困难。以上考虑风电-光伏功率相关性所建立的模型,数据量多、模型维度高、求解困难且结果不精确。

基于上述原因,本文首先把风电和光伏数据以对应日场景的形式逐日连接起来,得到风电-光伏序列以保持风电和光伏序列之间的相关性；由于风电-光伏序列数据量大、维度高,无法对此直接聚合,所以采用因子分析理论［14］将z-score 标准化的风电-光伏原始输出功率进行降维,以“水平分量+波动分量”的形式进行表征；再以“水平分量的聚合映射到原始序列聚合”的方式对低维水平分量进行近邻传播聚类。然后,引入极限学习机（ELM）［15］获取水平分量和原始功率序列之间的映射关系。最后,建立考虑风电-光伏功率相关性的因子分析-极限学习机聚合模型。

1 风电-光伏多维变量的因子分析模型构建与风电-光伏多分量的统一表征

因子分析是一项通过对多维变量提取关键因子进行降维的技术。首先,分析多维变量间的内部相关性,提取少量低维假想因子用于表征原始的多维变量。低维的假想因子可以反映原始多维变量的关键信息,可称其为公共因子。而本文所要聚合的风电-光伏原始序列维度高、波动性强,所以需要采用因子分析对风电-光伏功率变量进行降维处理。提取出若干公共因子,分为功率水平因子和功率波动因子。由于功率水平因子载荷高,对原始变量的方差贡献大,所以可用功率水平因子的线性表达式表示原始变量,再通过功率水平因子生成较为平滑的水平分量。因为功率水平因子占据着原始变量的大部分信息,反映了电源出力的输出水平,所以水平分量延续了原始序列的整体出力特征、波动特征和相关性。

1.1 风电-光伏多维变量的降维与因子分析模型构建

因子分析需要初始变量具有较高的相关性,可对初始变量进行KMO（Kaiser-Meyer-Olkin）检验和巴特利特（Bartlett）球体检验。当KMO 检验系数大于0.5,巴特利特球体检验统计值的显著性概率P＜0.05 时,才能进行因子分析。通常设多维变量的总体为X,其因子分析的一般模型为：

式中：X为标准化后的原始变量组成的向量；F为不可测的向量,由X的公共因子组成；ε为因子分析得到的非关键信息组成的向量,是X的特殊因子；A为成分矩阵,其中的因子载荷apm是第p个变量与第m个因子的相关系数,代表了彼此的相关程度,因子分析模型的详细介绍见附录A。

因子载荷矩阵的求解方法主要有以下3 种：主成分分析法［16］、主因子法［17］、极大似然估计法［18］。主成分分析法可以通过正交变换将原始数据当作存在相关性的变量转换为一组无相关性变量,常用于高维数据的降维,所以本文采用主成分分析法,计算步骤如下。

1）计算原始数据X的协方差矩阵Σ。

式中：λ1,λ2,…,λm为特征根；e1,e2,…,em为单位特征向量。

2）计算并按大小排列Σ的特征根λ1≥λ2≥…≥λp,再得到相应的单位特征向量e1,e2,…,ep；提取m（m≤p）个最大特征值和对应的特征向量（提取特征根大于1 的数值来确定m）,因子载荷矩阵A即可由式（3）得出。

由于因子载荷矩阵A的绝对值较为平均,不具有代表性。通过因子旋转,使载荷值呈现两级分化。旋转后的载荷矩阵为AR。此时公共因子与原始变量之间的关系可以作出物理上的解释,将公共因子Fj用原始变量进行表征,即

式中：βpq为得分函数的系数。

由于在p＞m时不能得到精确的得分,一般通过回归分析可以得到如下表达式：

式中：R为原始变量的相关系数矩阵。

将求得的因子得分系数的值代入式（4）便可以得到公共因子得分的估计值,进而根据式（1）求取公共分量。

1.2 计及风电-光伏因子分析模型的风电和光伏功率水平分量求解

式中：t=t1+t2,代表风电-光伏日场景集在该天的采样点总数,其中t1和t2分别表示风电和光伏功率在该天的采样点数。

本文采用中国西部某地区风电和光伏2019 年全年实测输出功率为输入数据,采样点间隔为15 min,由于西北地区晚间20：00 至第2 日07：00 无光照辐射,本文剔除光伏电站在此时段的输出功率。故而风电功率的采样点数为96,光伏功率的采样点数为52,即t1和t2分别为96 和52,t为148,c为365。

根据文献［19］构建的多能源同质化耦合模型可知,Pt,c可由“功率水平分量+功率波动分量+差异性随机分量+预测误差分量”统一表征（由于各分量实际由多个日场景构成,后文统一用“各分量+日场景集”表述）,如式（7）所示。

当Pt,c为原始功率时,预测误差分量场景集Ppreerr,t,c为0；Flev为水平因子,构成的公共分量称为水平分量日场景集Plev,t,c；Fflu为除了水平因子Flev外的其余m−1 个公共因子共同构成的波动因子矩阵,由其构成的公共分量则为波动分量日场景集Pflu,t,c；Pranc,t,c为差异性随机分量场景集；Az为A的第z列数据。

本文对风电-光伏标准化功率日场景集Pt,c进行因子分析,选取特征根大于1 的几个因子。采用方差最大法对因子进行旋转,使得少数几个因子均包含风电-光伏大部分信息。选用方差贡献率较大的几个因子作为功率水平因子,得到功率水平分量日场景集。其余的因子由于载荷值低,均作为功率波动因子,得到功率波动分量日场景集。为使模型便于计算,将差异性随机分量日场景集叠加至波动分量日场景集。风电-光伏因子载荷图和分量图分别如附录B 图B1 和图B2 所示。

2 因子分析-极限学习机的聚合模型构建与风电-光伏聚合序列的生成

ELM 适用于高维变量之间的拟合,大量研究表明,ELM 具有较强的学习表征能力,学习速度快、泛化能力强。上文已通过因子分析获得了水平分量日场景集,而本文最终需要得到具有风电-光伏原始功率特性的风电-光伏聚合序列。由于水平分量是由原始序列分解而来,其序列曲线基本跟随原始功率进行变化,反映水平分量与原始序列时刻都保持着强相关性。故可使用ELM 学习水平分量日场景集和原始日场景集的映射关系,构建相应的拟合模型,使得输出的风电-光伏聚合序列保持风电-光伏原始序列原有的相关性,从而构建出整体的因子分析-极限学习机的聚合模型,如附录B 图B3 所示。

2.1 因子分析-极限学习机的聚合模型构建

ELM 模型首先随机产生输入层权值和偏差,并通过广义逆矩阵理论得到输出层权重。随后ELM模型训练得到所有网络节点上的权值和偏差,此时测试数据利用求得的输出层权重便可计算出网络输出,从而完成对数据的拟合。 设样本{xs,ts|xs∈RD,ts∈Rm,s=1,2,…,N},其中,N为样本数,D为ts的维数。xs表示第s个数据示例,ts表示第s个数据示例对应的标记。记隐藏层输出为H(xs),其计算公式如下。

H(xs)=[h1(xs),h2(xs),…,hl(xs),…,hL(xs)]（8）

式中：hl(xs)为第l个隐藏层节点的输出,隐藏层可通过不同训练集获得不同的输出函数,适用于不同的隐藏层神经元；L为节点数。

在实际应用中,hl(xs)通常可表示为：

式中：s=1,2,…,N；g(ws,bs,xs)为基于ELM 通过逼近定理的非线性分段连续函数,其中,ws和bs分别为隐藏层节点上的权值和偏差。

经过隐藏层进入输出层,根据式（8）得到ELM的输出为：

式中：β=[β1,β2,…,βl,…,βL]T为隐藏层与输出层之间的权重组成的向量。

以上是ELM 从输入到输出的计算过程。但上述公式中的未知量有ws、bs、β,需要通过ELM 模型的训练机理得到上述3 个未知量。一般来说,ELM训练单隐层前馈神经网络分为两个主要阶段：第1阶段随机产生ws和bs,由此可根据式（8）和式（9）计算出隐藏层输出H；第2 阶段,通过训练样本集得到β值,首先需要保证其训练误差最小,可以用Hβ（Hβ是网络的输出,如式（10）所示）与样本标签T求最小化平方差作为评价训练误差,最优解则是该函数的最小解。

目标函数为：

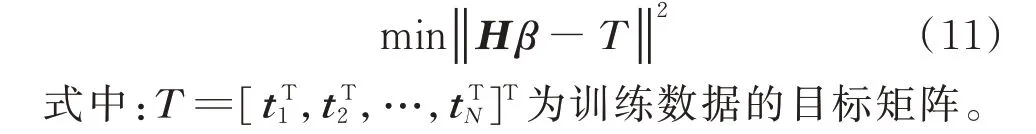
通过 ELM 的数学模型可知,输入层x1,x2,…,xN分别由水平分量日场景集中每个月的聚合日场景集所构成,输出层t1,t2,…,tN分别由每个月对应选取的原始日场景集所构成,故N等于12。随机赋值隐藏层节点,通过线性参数求解［20］的方法得到隐藏层与输出层间的输出权值与ELM 的内部权值。

2.2 计及风电-光伏功率相关性的风电-光伏聚合序列生成

基于因子分析得到的水平分量日场景集,通过ELM 得到风电-光伏聚合序列的步骤如下。

1）将全年的水平分量日场景集Plev,t,c逐月分为每个月的水平分量日场景集Plev,t,ch(h=1,2,…,12),ch为第h个月对应的天数。

2）对每个月的水平分量日场景集Plev,t,ch进行AP 聚类,每个月分别获得K(h)(h=1,2,…,12)类场景簇,设每类场景簇的场景数为n1,n2,…,nK(h)。通过随机数对每个月的水平分量日场景集Plev,t,ch进行采样,采样数均为2n。为了使样本更具代表性以及减少抽样误差,本文采取分层抽样法对每类场景簇抽样,从而得到各个月抽样的样本数为2nno/(n1+n2+…+nK(h)),o=1,2,…,K(h)。 当抽样数为小数时,对抽样数进行取整。

3）采样后即得到每个月的聚合日场景集Plev,t,2n,h,并将每个月前n天的聚合日场景集P1lev,t,n,h作为训练集的输入层,后n天的聚合日场景集P2lev,t,n,h作为测试集的输入层。由于采样日已确定,再从风电-光伏标准化功率日场景集Pt,c逐月分为每个月的原始日场景集Pt,ch,并在每个月的原始日场景集中对应选取2n天的原始日场景集Pt,2n,h。把每个月前n天的聚合日场景集P1t,n,h作为训练集的输出,后n天的聚合日场景集P2t,n,h作为测试集的输出。

4）将训练集的输入层和输出层导入ELM 中,随机赋值隐藏层节点,计算得到ELM 的内部权值。随后导入测试集的输入层和输出层,最后得到拟合功率日场景集Pnihet,n,h。并将其反标准化和矩阵转换,即分别得到风电聚合序列Pjuhewind和光伏聚合序列Pjuhepv。

根据上述步骤,针对本算例分别令n为4、7 和14,得到48 d、12 周、24 周的风电-光伏聚合序列,并将其与标准化的风电-光伏原始功率进行对比,如图1 所示。为了检测拟合偏差,本文采用残差平方和（residual sum of square,RSS）来定量比较拟合效果,RSS 的计算公式如附录A 所示,计算得到聚合48 d、12 周、24 周 的RSS 分 别 为18.26、12.13和7.96。

图1 风电-光伏序列拟合图Fig.1 Fitting diagram of wind power and photovoltaic power sequence

由图1 及RSS 指标可知,通过ELM 得到的风电-光伏功率拟合值与原始风电-光伏序列的RSS指标保持在较低水平。其中聚合48 d 偏差较大,这是由于输入的场景集较少,导致准确率较低；相反,聚合12 周及24 周输入的场景集增多,包含了原始风电-光伏场景集的大部分典型场景,故而拟合度高。从拟合的结果可以知道,本文采用的聚合方法得到的风电-光伏聚合序列在结果准确性上较高,并随着风电-光伏输入场景集的增多,输出风电-光伏聚合序列的拟合误差不断下降。

3 算例分析

本文将原始风电-光伏时序数据作为参照,对比分析K-means-MCMC、AP-MCMC 聚合方法单独对风电-光伏聚合结果和本文考虑风电-光伏相关性聚合结果的概率统计指标、相关系数以及仿真计算结果。本算例聚合方法得到的风电-光伏聚合结果如附录B 图B4 和图B5 所示。

3.1 多重评价指标

借助概率统计指标［21］、相关系数指标［22］和风电-光伏年度电量优化仿真计算等各项指标,与单独的聚合方法进行对比可以验证本文方法的准确性和可行性。一般情况下,和原始序列的各项指标越接近,聚合场景的准确性和可行性越高。

1）概率密度函数指标

概率密度函数（PDF）能够反映不同时间尺度下和不同时间段的风电-光伏序列的概率分布情况,是衡量时间序列的基本统计指标。本文主要统计风电或光伏出力与装机容量之比在每个单位长度的概率分布情况,计算公式如下：

式中：yn为风电/光伏出力与装机容量之比；Pr为yn在(r−1%)～r出 现 的 概率；num(yn)为yn在(r−1%)～r出现的次数；Ny为yn取值的总数。

2）自相关系数指标

自相关系数（ACC）描述了不同时滞范围之内风电-光伏序列与自身原始序列的相关程度,能够精确地体现风电-光伏序列的平稳性和趋势性。首先,将原时间序列X滞后k个步长,产生新的时间序列Y；接着,使用自相关系数公式计算两者之间的自相关系数ρXY,具体如式（13）和式（14）所示。

3）短时波动率指标

短时波动率统计了风电-光伏功率在短时步长（15 min,1 h）下的变化量分布情况,用于检验时间序列的波动特征。其变化量ΔP(t)的分布计算公式为：

式中：Pmax(t)为在短时步长时段内功率的最大值；Pmin(t)为在短时步长时段内功率的最小值；tp,min和tp,max分别为功率初始时刻到Pmin(t)和Pmax(t)出现时刻的时间长度。

4）相关系数指标

为了验证聚合后得到的风电-光伏聚合序列的可行性,风电-光伏序列聚合前后的相关性指标也需要保持一致。一般用相关系数来表示变量之间的相关性强弱,常见的相关系数有Pearson 相关系数、Kendall 相关系数及Spearman 相关系数。其中,Pearson 相关系数是一种线性相关系数,可以直观反映两个随机变量的线性相关程度大小,其取值范围为−1～1。Kendall 相关系数是用来测量两个随机变量相关性的统计值,可以描述两个随机变量变化趋势的一致性,能够在一定程度上反映非正态分布的随机变量相关性。Spearman 相关系数是用来测量两个线性随机变量的相关指数,可以很好地描述非正态分布随机变量的非线性相关关系,属于非参数统计方法。由于风电功率具有非高斯性,并且风电波动性强,容易出现异常值。而异常值的秩次通常不会有明显的变化,对Spearman 相关系数的影响也非常小,故本文选用Spearman 相关系数。

3.2 聚合结果的可行性检验

图2（a）和（b）分别展示了本文方法与对比方法的风电、光伏功率的PDF 指标结果。图中清楚地展现了各种聚合结果的特征,且风电和光伏功率的PDF 特征是一致的：K-means-MCMC 聚合方法和AP-MCMC 聚合方法波动均较大,且曲线波形较为贴近。其中AP-MCMC 聚合方法相对K-means-MCMC 聚合方法更接近原始数据,这是因为Kmeans-MCMC 聚合方法的聚合中心不稳定。而本文方法得到的聚合序列PDF 指标误差明显小于对比方法,并保持在合理范围内。与48 d、12 周聚合序列相比,24 周聚合序列曲线更加平滑,这是因为随机变量在各状态下的概率分布呈现均匀分布,原始序列的PDF 曲线呈现平滑趋势,故而当聚合序列的长度增加时,其PDF 曲线和原始序列在大部分情况下更加接近。

图2 风电和光伏功率的PDF 对比Fig.2 PDF comparison of wind power and photovoltaic power

风电和光伏功率的ACC 对比如图3 所示,由图3可以看到,两种单独聚合方法获得的聚合场景的时变特性与原始时序数据相差过大。风电自相关系数曲线与光伏功率自相关曲线所显示的结果略有差异。图3（a）显示的是风电ACC 指标的对比情况,图中曲线表明不同聚合方法下的ACC 指标与原始序列相比,均有一定的误差。但考虑相关性的聚合方法得到的聚合结果与原始序列的黏合程度均较高,ACC指标下降趋势均较为平缓。图3（b）显示的是光伏功率的ACC 指标对比情况,由于光伏功率本身的时变特性较为稳定,所以不同聚合方法得到的聚合序列与原始序列基本接近。但本文所提方法的ACC曲线与原始序列集中在一条曲线上,精确度更高。

图3 风电和光伏功率的ACC 对比Fig.3 ACC comparison of wind power and photovoltaic power

风电和光伏功率短时波动率对比如图4 所示。在图4 中,两种单独聚合结果的倾斜角度小、上升速度慢,风电最大波动达到5%,光伏功率最大波动达到8%,说明聚合结果的功率波动较强。而本文所提方法得到的3 种不同长度的聚合序列在短时波动特征上均贴近原始时序数据的波动指标,倾斜角度大、上升速度快,风电最大波动达到3%,光伏功率最大波动达到6%,说明聚合结果和原始序列的功率波动均较弱,能较好地保留原始序列的波动特性。

图4 风电和光伏功率的短时波动率对比Fig.4 Comparison of short-term volatility between wind power and photovoltaic power

不同聚合方法下不同季节风电-光伏相关系数的对比如图5 所示,可以看出与未考虑风电-光伏功率相关性聚合结果相比,考虑风电-光伏功率相关性的相关系数与原始风电-光伏序列相关系数值无明显变化,说明相关性保持一致。不过ACC 会随着聚合长度减少而逐渐变强或变弱,这是由于聚合长度减少,与原始风电-光伏序列之间的关联性不断减弱,相关性降低；另外,春、秋季节各聚合序列的风电-光伏功率相关性均处于正相关,而夏、冬季节则存在负相关并且相关性并不一致,这是由风电-光伏功率的资源特性（全年风力强,夏季因雨季光照少,冬季光照弱）所决定的。

图5 不同聚合方法下不同季节风电-光伏相关系数对比Fig.5 Comparison of wind power and photovoltaic power correlation coefficients with different aggregation methods

利用电力仿真计算系统［8］,分别对风电-光伏原始时序数据、聚合48 d、聚合12 周、聚合24 周、Kmeans-MCMC 聚合序列与AP-MCMC 聚合序列进行评价指标计算。表1 和表2 中的风电和光伏发电总量为理论发电量,风电-光伏接纳电量是风电-光伏发电总量减去弃风、弃光电量。表3 和表4 中展示了不同模型评价指标的相对误差。

表2 光伏功率在不同聚合方法下的评价指标Table 2 Evaluation indices of photovoltaic power with different aggregation methods

表3 风电功率在不同聚合方法下的评价指标相对误差分析Table 3 Relative error analysis of evaluation indices for wind power with different aggregation methods

通过对比表1 至表4 中的数据可以发现：本文方法下聚合48 d 所需的仿真计算时间最短,仅为全年时序仿真计算时间的2.9%。但是,由于聚合长度较短,得到的典型场景少,不能完全反映水平分量和原始序列之间的映射关系,计算得到的风电-光伏接纳总量比例相比对照组具有较大误差。而聚合24 周下的风电、光伏接纳总量比例和对照组相差无几,这是因为选取了更多的典型场景作为整条序列,但与此同时计算时间也大大增加,降低了仿真计算的效率。K-means-MCMC 聚合方法的整体指标均高于对照组,而AP-MCMC 聚合方法却低于对照组,这是因为K-means-MCMC 聚合方法的聚类中心是随机选取的,风电-光伏功率较高的场景选取较多导致指标过高；AP-MCMC 聚合方法是将全部数据点当作潜在的聚类中心,数据两两间构建网络,通过网络传递信息选取样本中心,从而选取典型场景。且由于全年风电-光伏时序数据整体呈现较低水平,故而在功率较低的场景中选取较多,导致仿真计算得到的指标过低。综上：本文方法的仿真计算指标要优于对照组,并随着聚合长度的增加,各项指标更加贴近于对照组,但计算时间也在不断增加。

表1 风电功率在不同聚合方法下的评价指标Table 1 Evaluation indices of wind power with different aggregation methods

表4 光伏功率在不同聚合方法下的评价指标相对误差分析Table 4 Relative error analysis of evaluation indices for photovoltaic power with different aggregation methods

3.3 水平分量聚合长度对风电-光伏聚合序列的影响

本文对风电-光伏水平分量全年序列按各个月分别聚合了4、7、14 d,对应得到48 d、12 周、24 周的风电-光伏水平分量聚合序列。不同长度的聚合序列构成了不同样本量的训练集,概率统计指标表明：聚合长度越长,其各项指标越接近于原始风电-光伏时序数据,说明训练集的样本量越大,越有利于聚合结果的精确性和可行性。根据仿真计算结果,分析不同聚合序列长度对风电-光伏接纳电量、风电-光伏接纳总量、弃风弃光率指标的影响：随着聚合长度的增加,以上3 项仿真计算指标的计算误差在原始数据的基础上上下波动,但绝对值处于逐渐减小的趋势。

同时,仿真计算时间也随着聚合序列长度的增加而变长。电力系统仿真计算需要从计算精度和计算时间来考虑,满足计算误差的前提下,选取计算效率最优的聚合长度。从本文的仿真计算结果得到,最优的水平分量聚合长度为12 周。

4 结语

通过因子分析-极限学习机聚合模型生成的聚合序列,以某省级电网为例,与对照组相比得到以下结论。

1）本文所提的聚合方法在理论部分不同于单独聚合方法。首先对风电-光伏功率进行因子分析,得到的水平分量可以对风电-光伏序列统一表征,且包含了风电-光伏发电系统相同部分的信息,保持了风电-光伏序列的相关性。再引入ELM,将得到的水平分量映射到聚合序列,最后反标准化得到风电、光伏聚合序列。

2）随着风电-光伏水平分量聚合长度的增大,得到的风电-光伏聚合序列更加趋近原始风电-光伏序列的数据特征。证明了聚合长度的增加可以提高仿真计算的准确性,但与此同时计算效率也在降低。从本文算例指标可以得到,聚合序列长度为12 周最为有效,既保持了风电-光伏原始序列的概率统计特性和相关性,又使得计算效率提高到较高的水平,具有实际工程意义。

本文所采用的聚合模型适用于两场站间的时序聚合,如何应对相关性更加密切复杂的多场站聚合还需深入挖掘；且所建模型考虑的是时间相关性,由于电力系统仿真计算涉及多区域多场站,考虑空间相关性的网格划分与聚合亟待解决。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。