附加应力随时间变化的组合桩型复合地基固结解答
2021-12-10武崇福李文雪李旭阳马进学王建刚
韩 毅,武崇福,李文雪,李旭阳,马进学,王建刚
(1.中交隧道局华中工程有限公司 湖北 武汉430014;2.燕山大学 建筑工程与力学学院,河北 秦皇岛066004)
0 引言
复合地基处理方法在工程中应用较多,随着施工技艺的发展,复合地基也从单一型向多桩型转变。常见的组合型复合地基如透水桩-不透水桩复合地基,可以用于加固滨海地区高速公路的软弱路基。其中透水桩可加快路基土的排水固结,不透水桩可提高路基土的强度。组合型复合地基在工程中应用较多[1-2],室内模型试验也研究了组合型复合地基的受力与变形特性[3]。有些专家学者研究了组合排水桩复合地基的固结理论:叶观宝[4]建立了水泥搅拌桩和塑料排水板联合使用的组合型复合地基的固结微分方程,并得到了解析解。Lin X[5]针对梅花形布置的排水板-粉喷桩加固地基,推导了瞬时加载下排水粉喷复合地基的平均固结度表达式。秦康[6]将砂井联合水泥土桩复合地基简化为水泥土搅拌桩为中心的轴对称固结模型,得到了单级加载和附加应力梯形分布下的组合型复合地基的固结解析解。于春亮[7]考虑了透水桩的固结变形,推导得到了瞬时加载下透水桩-不透水桩复合地基固结度表达式,并分析了桩的井阻和压缩模量等因素对固结速率的影响。杨涛[8]考虑了碎石桩的固结变形和桩的扰动区渗透系数沿径向线性变化等因素,建立了瞬时加载下组合渗流碎石桩-不排水桩固结方程。江培兵[9]考虑外部荷载随时间变化和桩的涂抹效应,建立了两种解析模型下长板-短桩的孔压和固结度解析解。杨涛[10]将刚柔性长短桩复合地基与下卧层的固结问题简化计算为成层的天然地基的一维固结问题,得出各层土的平均固结度解答。Yu C L[11]建立组合渗流碎石短桩和CFG长桩的固结模型,将碎石短桩与CFG桩共同加固区域的土简化成渗透系数较大的均质土,计算加固区内双层地基土的平均固结度。卢萌盟[12]考虑了散体材料桩的置换率,推导了散体材料桩-不透水桩多元组合桩复合地基的固结解答,讨论多元组合桩型复合地基的固结性状。
目前关于透水桩-不透水桩复合地基的固结理论研究,基于瞬时加载建立了考虑桩体固结变形、涂抹效应和径向井阻等因素的组合型复合地基固结解析解,但是没有考虑附加应力的时间效应。因此,本文考虑荷载随时间变化,建立了分级加载下附加应力随时间变化的组合桩型复合地基固结度解答,并通过参数分析,研究了分级加载下组合桩型复合地基的固结规律。
1 固结模型
组合透水-不透水桩复合地基采用正方形布设方式,每四根透水桩(不透水桩)的中心布设一根不透水桩(透水桩),桩间距为S,如图1所示。


图2 固结模型平面图Fig.2 Consolidation model plan
图3为固结模型剖面图,复合地基顶面排水,底面不排水,桩身长度等于土层厚度H。kv和kh分别是未扰动土的竖向和横向渗透系数,ks1和ks2分别为透水桩和不透水桩涂抹区的渗透系数,kpv和kph为固废料透水桩的竖向和横向渗透系数,q(t)为作用在复合地基顶部的均布荷载,在地基中引起的附加应力随时间变化,沿深度均布。

图3 固结模型剖面图Fig.3 Consolidation model profile
上部荷载q(t)是一个时间函数,表示上部荷载分级施加,总应力随时间变化。上部荷载施加到刚性混凝土板上,传递到地基土中,在地基土中引起大小为σi(t)、沿深度均布的力。σi(t)为第i(i=1,2,…)级荷载加载完成后在地基中引起的附加应力的大小,σu为加载完成后地基中的附加应力值,如图4所示。
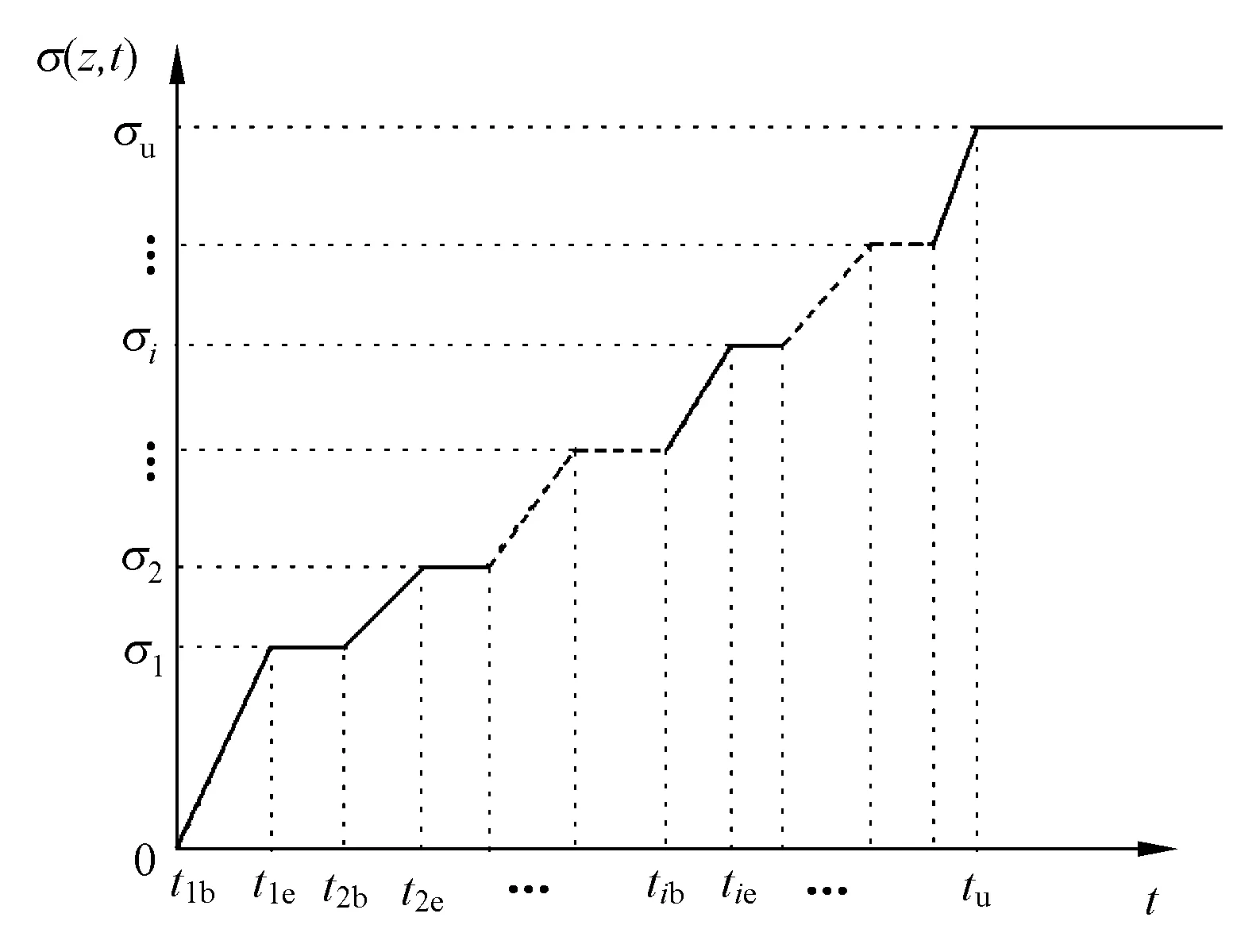
图4 附加应力随时间变化Fig.4 Additional stress varies with time
本文推导基于以下基本假设:1)等应变条件成立;2)透水桩和桩间土是饱和的,渗流符合达西定律;3)上部荷载分级线性施加,在地基中引起的附加应力随时间变化,沿深度均匀分布。
对于组合渗流透水桩-不透水桩复合地基,由平衡条件和等应变假定有

(1)

(2)


(3)
碎石桩和桩间土的固结方程:

(4)
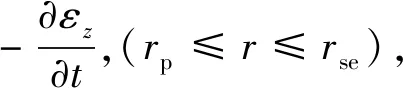
(5)
由式(1)、(2)、(3)得,

(6)
Ecomp=(1-m1-m2)Es+m1Ep+m2Ec,
(7)
边界条件:

(8)

(9)

(10)
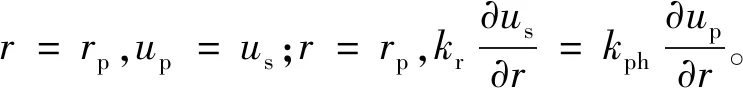
(11)
初始条件:

(12)
参照杨涛解关于组合渗流碎石桩复合地基固结方程的求解方法,根据方程式(4)~(7)和边界条件式(8)~(12),整理得

(13)
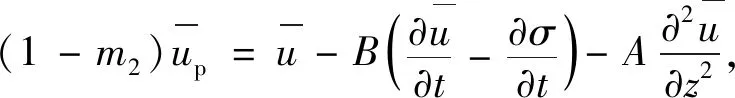
(14)
式中,
C=(1-m1)T+1;
考虑上部荷载单级施加引起地基中的附加应力随时间变化,沿深度均匀分布。分级加荷下附加应力表达式如下:
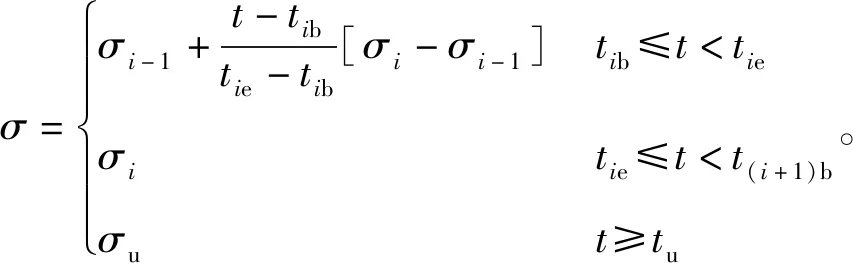
(15)
2 孔压求解
2.1 第一加载阶段孔压解
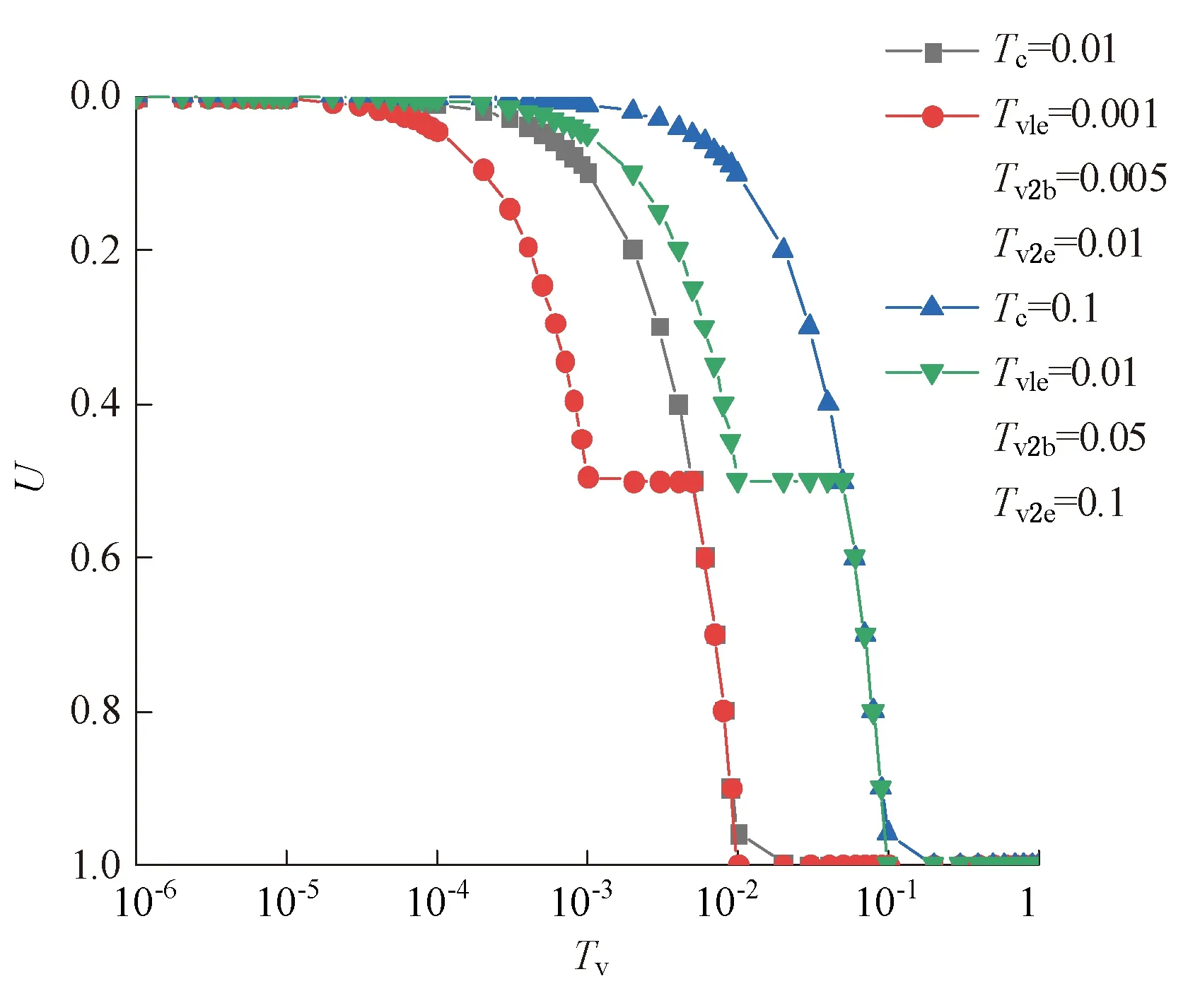
荷载线性施加时,即t1b≤t (16) 将式(16)代入(14)有 (17) 利用边界条件式(9)解得 (18) 此时, (19) (20) 式中, (21) (22) 将初始条件式(12)代入式(16)中,得到 (23) (24) 利用式(20)和(24)关于Tn(t)的常微分方程,可得到解的形式如下, (25) 将式(25)代入式(19)得 (26) 恒载阶段,即t1e≤t (27) 将式(27)代入式(13)中,满足边界条件式(8)。 在t=tc时满足连续条件: (28) 即 (29) (30) 式(30)代入式(27)中,得到 (31) 第i个加载阶段,即tib≤t (32) 代入方程(14)中,则 (33) 由边界条件式(9)可得 (34) 代入式(32)得 (35) 结合式(13)和(14),将式(34)代入式(13)中,整理后得 (36) 式中,βn同式(19), (37) 孔压随时间连续,当t=tib时, (38) 即 (39) (40) 利用式(35)和(40)关于Tn(t)的常微分方程,可得到解的形式如下, (41) 式(41)代入式(34)有 (42) 恒载阶段时tie≤t (43) 式(43)满足连续条件, (44) 即, (45) (46) 代入式(43)中得 (47) 加载完成后,最后一个线性加载阶段完成后地基的孔压, (48) (49) 第1个加载阶段(0≤t (50) 第1个恒载阶段(t1e≤t (51) 第i个加载阶段(tib≤t (52) 第i个恒载阶段(tie≤t (53) 加载完成后, (54) 只考虑上部荷载单级施加时,t1e=tc,σ1=σu,此时解可以退化到下面的形式。 线性加载阶段,即0≤t (55) 恒载阶段,即t≥tc时, (56) 进一步地,当上部荷载瞬时施加时,tc=0,此时解可进一步退化, (57) 图5给出4种加载速率下复合地基的固结曲线,竖向固结时间因子Tc反映加载完成时的时间参数。计算时有四种工况:Tc=0(瞬时加载)、Tc=0.001、Tc=0.01和Tc=0.1。计算单级加载下组合透水桩-不透水桩复合地基的固结度并绘制成曲线,结果发现,Tc=0时固结最快,Tc越大,复合地基的固结速率越慢。 图5 不同加载速率下的固结曲线Fig.5 Consolidation curves at different loading rates 图6将单级加载和两级加载下复合地基的固结曲线进行对比,分析不同加载历程下复合地基的固结特性。当总的加载时间一定时,上部荷载单级施加和分两级施加复合地基固结所需要的总时间基本一致。每级荷载大小相同,计算结果发现,两级加载的第一个加载阶段与单级加载的初期阶段相比,在第一级加载下复合地基的固结速率快于单级加载的前半部分,而后半部分两种加载方式的固结曲线重合。说明分级加载会在加载初期加快地基的固结,使复合地基较早变密实,有利于地基的稳定。 图6 两级加载下的固结曲线Fig.6 Consolidation curvs under two-stage loading 图7是Tc=0.01时不同的不透水桩土模量比下的固结曲线,从图上可以看出,考虑荷载随时间变化时,不透水桩土模量比越大,组合型复合地基固结越快。 图7 CFG桩土模量比对固结的影响Fig.7 Effect of CFG pile-soil modulus ratio on consolidation 图8为kph/kh不同时组合型复合地基的固结曲线,与图中也给出文献[8]在kph/kh=1 000时的固结曲线。由图8可知,单级加载时总应力随时间变化,kph/kh越大,组合型复合地基固结速率越快。文献[8]的解答没有考虑荷载随时间的变化,高估了组合型复合地基的固结速率。 图8 单级加载时径向井阻对固结的影响Fig.8 Influence of radial resistance on consolidation under single stage loading 本章运用解析方法,得到分级加载下的组合透水桩-不透水桩复合地基的固结度解答,进一步完善了组合桩型复合地基的固结理论。主要得到以下结论: 1)分级加载时附加应力随时间变化,组合透水桩-不透水桩复合地基的固结速率远远慢于瞬时加载,且加载时间越长,复合地基固结速率越慢。 2)两级加载的固结曲线呈阶梯形分布,当每级荷载大小相同时,固结所需要的总时间与单级加载相同,第一个加载阶段明显加快了加荷初期的固结速率。 3)考虑荷载随时间变化时,不透水桩土模量比和透水桩的径向渗透系数越大,组合型复合地基固结速率越快,均远慢于瞬时加载。






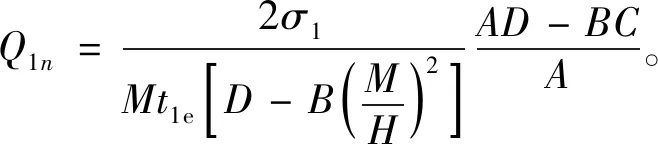










2.2 任意加载阶段孔压解
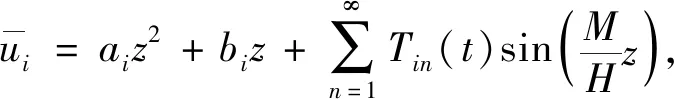



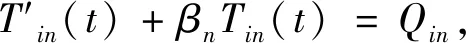

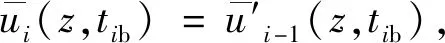
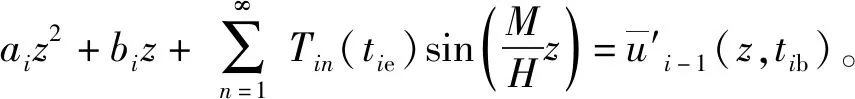








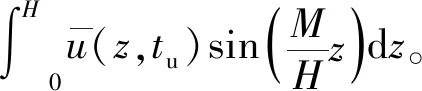
3 固结度求解
3.1 整体平均固结度解答
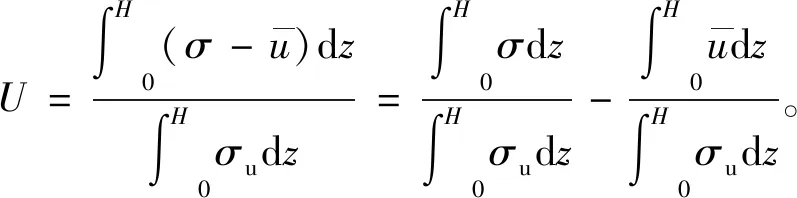





3.2 解的退化


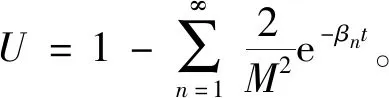
4 算例分析




5 结论
