电磁谐波活齿传动系统柔轮内共振分析

任玉波，边维东，马耀阳，宛 瑞

(燕山大学 机械工程学院，河北 秦皇岛 066004)

0 引言

传统电机都是以高速旋转的，这种高转速状态有时不能直接满足工业设备运行的要求，大部分的电机需要与减速机构配套使用。为了降低传动系统的体积、重量以及累计间隙误差，笔者提出了一种新型的复合传动系统——电磁谐波活齿传动系统，它同时兼有电机和减速器的功能，多齿啮合，大减速比运动传递，电流调控，由于该传动系统中没有高速旋转的机械部件，因此可以获得更快的响应能力[1]。

该传动系统是利用柔轮的变形来推动活齿与中心轮啮合来传递动力的，而柔轮是在电磁力作用下发生变形，因此，柔轮不可避免地会产生振动[2-3]。2009年，刘彦琦等人[4]建立了存在线性外阻尼的加速黏性传动带空间横向振动非线性动力学方程，采用多尺度法与Galerkin离散原理求解方程并分析了系统的1∶1内共振现象与分岔、混沌动力学特性。2013年，王延庆等人[5]对薄壁圆柱壳内共振和运动分岔进行了分析，表明轴向运动复合材料薄壁圆柱壳的幅频特性曲线表现出硬特性，系统能量在两个模态之间相互传递，产生了内共振。2014年，黄慧春、张艳雷等人[6]利用Euler-Bernoulli模型简化了平面内横向振动的弹性管路模型，采用多尺度法对该系统在固支边界条件下的2∶1内共振进行了分析。2015年，张宇飞等人[7]对轴向运动层合薄壁圆柱壳内共振进行了数值分析，表明激振力对内共振的影响较大。2019年，胡宇达等人[8]分析了在外激励力与磁场作用下轴向运动铁磁梁的磁弹性非线性内共振现象，并利用数值的方法进行了证明。这些文献对于柔轮的非线性振动特性研究大多都在模态相差比较大的范围内，当两模态的激振频率相靠近时，模态之间会出现强烈的耦合作用，对柔轮的非线性振动形态会产生很大的影响。

本文根据Donnell非线性简化壳理论，建立了系统存在阻尼、动态弹性模量、结构几何非线性情况下的柔轮非线性振动微分方程，采用Galerkin理论和Lyapunov一次近似理论对微分方程中的空间和时间变量进行拆分，分析柔轮在内共振时的受迫振动及稳态周期不同参数对模态振幅幅频特性的影响。掌握电磁谐波活齿传动系统动力学行为，在避免出现较大振动方面可为柔轮参数设计提供科学依据。

1 柔轮的非线性振动方程

如图1所示，在柔轮上取一个微元，u、v、w分别表示柔轮在电磁力作用下x、θ、r方向位移，qx、qθ、qr为在x、θ、r方向上作用在中面微元的外载力分量，3个方向对应的惯性力项分别为(-ρh∂2u/∂t2)、(-ρh∂2v/∂t2)、(-ρh∂2w/∂t2)，R为柔轮半径，ρ为柔轮材料密度，h为柔轮厚度，t为时间函数。

图1 柔轮微元变形与单元受力情况Fig.1 Micro element deformation and stress of flexspline

由于柔轮一方面受到电磁力的作用，另一方面又受到活齿相反的力的作用，但活齿作用力在一定程度上抑制柔轮的振动，本文分析柔轮振动最不利的情况，因此忽略活齿作用力。利用柔轮几何方程的非线性部分[9]，建立柔轮非线性径向振动微分方程：

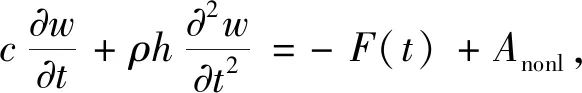
(1)

式中，Dij(ω)为柔轮弯曲刚度；Bij(ω)为磁场-柔轮耦合刚度；c为阻尼系数;F(t)为柔轮受到的径向电磁激振力[10];Anonl为微分方程的非线性项，表达式为

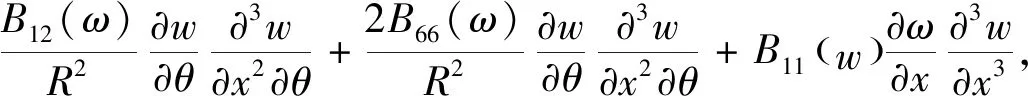
(2)

式中，Aij(ω)为柔轮拉伸刚度。

由于柔轮的轴向振动对整个激波器的影响较小，而影响较大的是径向振动，根据Donnell理论，为了提高运算效率且不影响精度，本文取两个相近的径向模态(M=2,N=n=6)对柔轮的非线性动力学进行分析。柔轮的径向位移函数为

Bm,n(t)cos(nθ)]，

(3)

式中,Am,n(t)、Bm,n(t)为柔轮的广义模态变量；Wm(x)为柔轮的径向振型函数；m为径向半波数；n为节径数。

根据Galerkin理论，对式(1)离散化，并定义柔轮径向位移的加权函数为

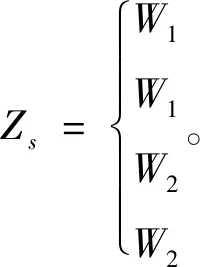
(4)

将柔轮的位移表达式(3)代入柔轮的非线性振动微分方程(1)中，并且乘以柔轮径向位移加权函数有

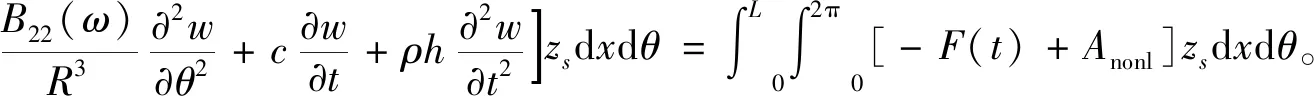
(5)

利用MATLAB软件对式(5)进行积分求解，选取参数：θ=π/24、F(t)=20 N、R=34.5 mm、L=120 mm、h=0.2 mm。

将式(5)中复杂的积分常数去除，经整理变换得到4个系数仅含1个广义坐标的二阶模态方程如下：

以上4式中，A1,6、A2,6、B1,6、B2,6是关于时间t的函数模态振幅；Si、Hi(i=1,2,…,15)为整理变换以后的积分系数，且其中的S15、H15是与电磁力F(t)的大小有关的系数；S1、S3、H1、H3是与柔轮的阻尼系数有关的系数。

2 多尺度法求解非线性方程组

根据前述，选择第一、二阶模态进行分析，令A1,6=B1,6、A2,6=B2,6，由于S3、H3、S4、H4的值相比其他系数小得多，可将其忽略不计，故将模态方程式(6)简化为

(7)

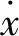
x1=A1,6=B1,6,x2=A2,6=B2,6,

F1=S15(6θ0),F2=H15(6θ0)，

a0=S5+S9,a1=S6+S10+S11,

a2=S7+S12+S13,a3=S8+S14，

b0=H8+H14,b1=H7+H12+H13,

b2=H6+H10+H11,b3=H5+H9。

采用多尺度法对模态方程式(7)进行摄动分析，令其一致渐进解为

(8)

式中，xij(i,j=0,1,2)为摄动未知函数，T0=t，T1=εt为时间变量，且尺度不同；T0为柔轮圆柱壳第i阶固有频率ωi引起的快时间尺度；T1是由三相绕组激励、阻尼以及径向振动微分方程的非线性项导致的相位、振幅的慢时间尺度。

为了分析柔轮圆柱壳两阶模态在三相绕组磁场力激励下发生1∶1内共振的情形，则产生这种运动状态需要满足的条件有

ω≅ω1，ω≅ω2，ω1≅ω2。

(9)

引入解谐参数σ1、σ2可更方便地分析1∶1内共振的情形，并且可以准确地表示上述频率之间的关系。用σ1表示二阶频率向一阶频率的靠近程度，σ2表示三相绕组激振频率向一阶频率的靠近程度，则令各阶频率与解谐参数之间的关系为

(10)

则，当ω1和ω2相接近时，σ1近似为0。

将尺度不同的时间变量定义为独立变量，引入微分算子，在式(8)中分离虚部与实部，得幅值dn和相位αn的关系式为

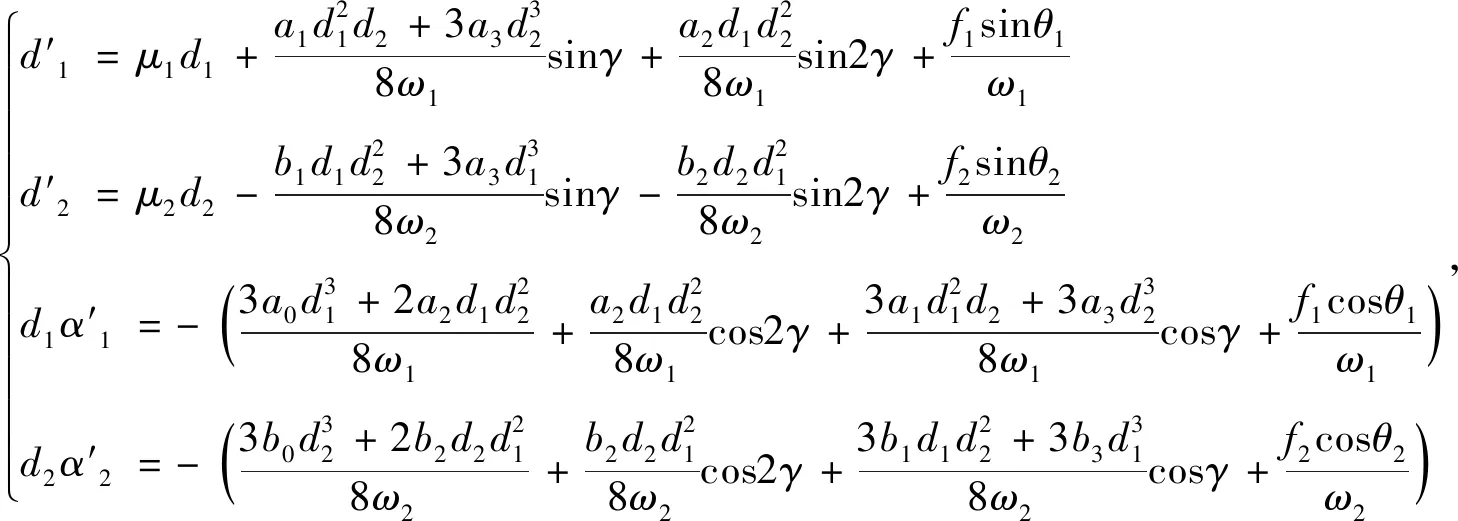
(11)

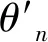
当幅值dn和相位θn为常数时，对应于系统的稳态响应，则在稳态响应存在下，幅值dn与新相位θn需要满足如下条件：

(12)

本文只对初相角γ=0时进行分析，当γ=0时，sinγ=0、cosγ=1、γ=θ1-θ2=0，将其代入式(11)，得到关于d1、d2的二元六次方程组：

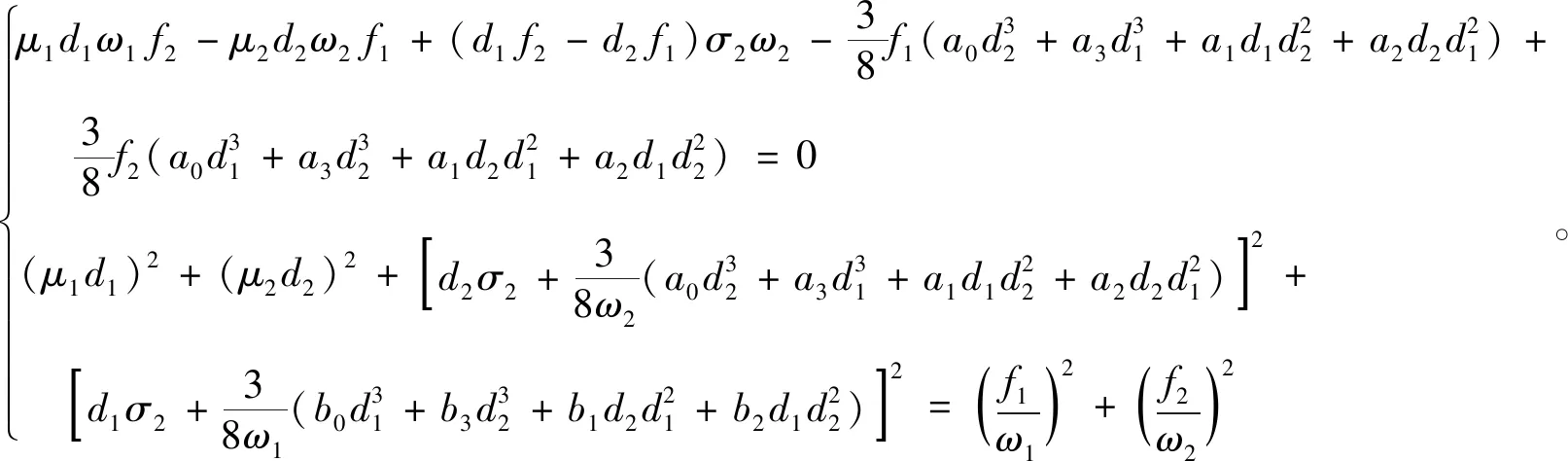
(13)

3 柔轮1∶1内共振下的幅频特性曲线分析

选取参数γ=0、ε=0.01、c=12.25、ω1=1 082.92 Hz，ω2=1 086.09 Hz，根据式(13)，利用MATLAB软件绘制出激振力F(t)=20 N时振幅d1、d2的幅频特性曲线如图2所示。

图2 激振力F(t)=20 N时振幅d1、d2的幅频特性曲线
Fig.2 Amplitude frequency characteristic curve ofd1andd2amplitude when excitation forceF(t)=20 N

由图2可看出，在电磁激励力频率与一阶固有频率靠近时，系统的两阶模态均被激发，幅频特性曲线表现为软特性并且有多个解分支，两阶模态的响应幅值大小相近，且均有4个解分支和较大的分支①，一阶模态有②、③、④半椭圆形状分支，二阶模态有一个包含封闭环的分支③，和②、④半椭圆形状分支。当σ2/ω1=0时，两阶模态的响应幅值均增加；当σ2/ω1=4时，两阶模态的响应幅值变化差异变大，一阶模态对应的解支①逐渐减小，二阶模态对应的解支①逐渐增大；当σ2/ω1=5.1时，幅频特性曲线出现多个解分支，也即解支③，一阶模态中解支③的两个分支随着频率比的增大而增大，二阶模态则出现了封闭环解；当σ2/ω1=8.4和σ2/ω1=9.2时，两阶模态又依次出现半椭圆形分支②、④，两个分支的上下两分支随着频率比的增大，变化相反。两阶模态的变化存在跳跃性，一阶模态在上半支，二阶模态则在下半支，反之亦然。

根据式(13)，将d1、d2转换成模态振幅，令σ2/ω1=5，得ω=1 137.07 Hz，并绘制出两组模态振幅的时间响应曲线如图3所示。

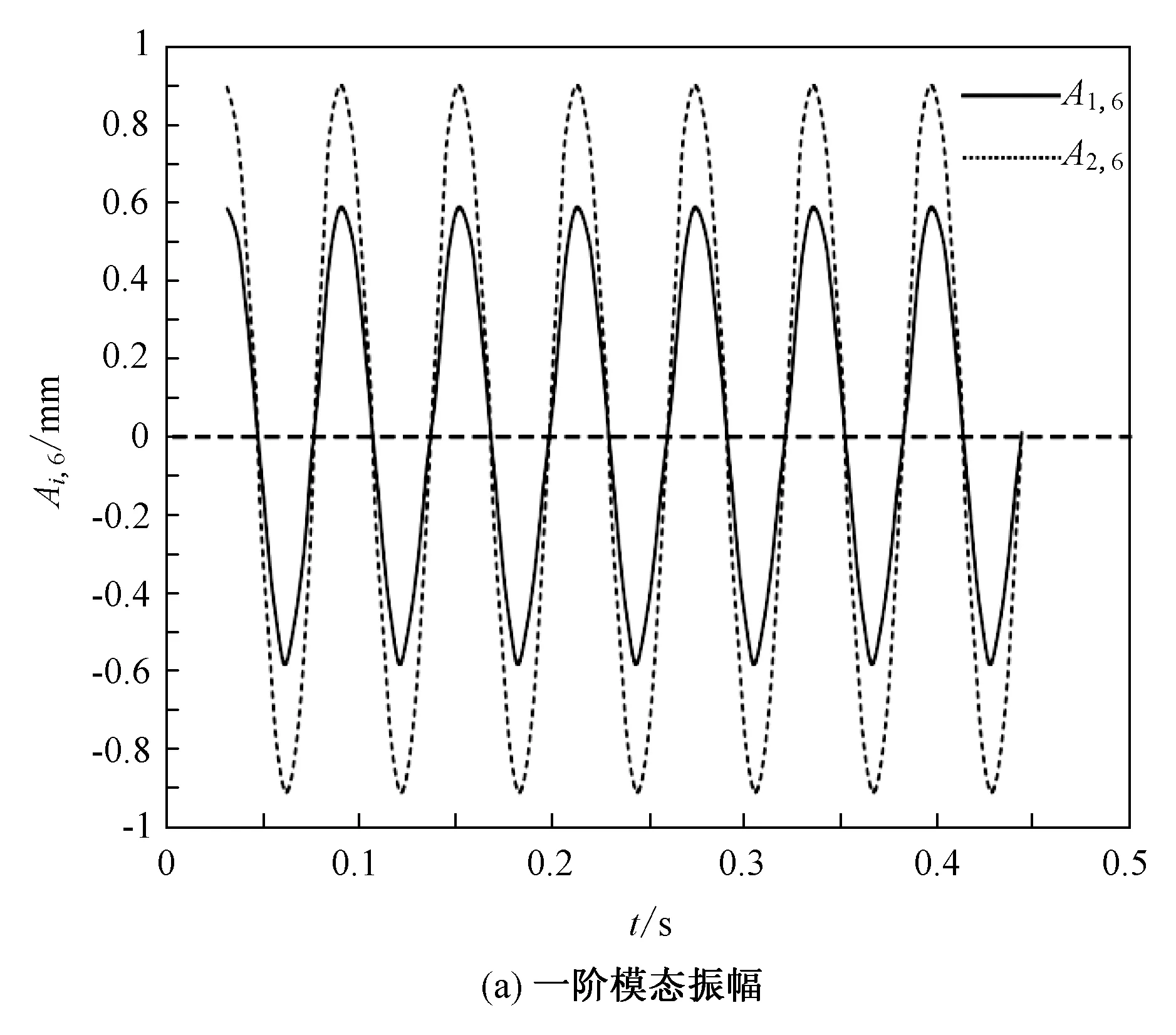
图3 激振力F(t)=20 N时两组模态振幅的时间响应曲线Fig.3 Time response curves of two groups of modal amplitudes when excitation force F(t)=20 N

从图3中可以看出，在激振力相等的情况下，两阶模态的响应幅值是连续变化的，系统的响应在两阶模态中不停地跳跃。由于两阶模态频率与固有频率十分接近，说明系统存在1∶1内共振现象。

4 性能参数对模态振幅幅频特性的影响

4.1 小参数对模态振幅幅频特性的影响

由式(8)可知，小参数ε的变化会影响振幅d1、d2向模态振幅A1,6、A2,6的转化，由于以振幅d1、d2为纵坐标的幅频特性曲线不能准确地表达出小参数的变化带来的影响，因此需要用模态振幅A1,6、A2,6为纵坐标。根据式(8)、式(13)，选取参数ω1=1 082.92 Hz、ω2=1 086.09 Hz、c=12.25 Nsm-3，则可绘制稳态解在频率比σ2/ω1变化下，激励力F(t)=25 N时，由于小参数ε的改变带来的幅频特性响应曲线的改变(广义坐标下)，如图4所示。

由图4可看出，当ε=0.001时，响应曲线的一条解支接近直线，另外的半圆形解分支也较小，曲线较为简单；当ε=0.02时，曲线开始变弯曲，共振区间变大，半圆形解分支也开始变大；当ε=0.04时，曲线复杂，非线性较强，两阶模态的解分支比较完整，模态响应值不停地在不同解支中跳跃，说明模态间能量传递的不规律性较强。因此，小参数ε越大，响应曲线越复杂，响应模态振幅值越大，二阶模态响应曲线的环解变大，共振区间变小，动力学行为越复杂；随着小参数ε的减小，两阶模态响应曲线越平滑，系统非线性性质越弱，逐渐接近线性，说明能量在模态间传递平稳。

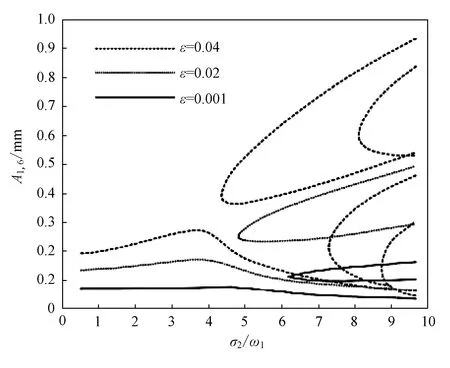
图4 小参数ε变化时模态振幅A1,6、A2,6的幅频特性曲线Fig.4 Amplitude frequency characteristic curve of A1,6 and A2,6modal amplitudes when small parameters change

4.2 阻尼系数对模态振幅幅频特性的影响

选取参数ε=0.01、ω1=1 082.92 Hz、ω2=1 086.09 Hz、F(t)=25 N，阻尼系数选取c=125 Nsm-3、c=12.25 Nsm-3、c=300 Nsm-3。根据式(8)、式(13)可绘制稳态解在频率比σ2/ω1变化下模态振幅A1,6、A2,6的幅频特性曲线(广义坐标下)，如图5所示。

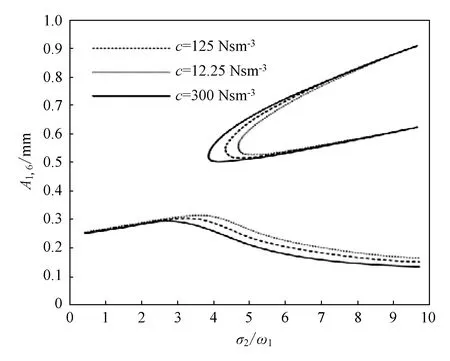
图5 阻尼系数c改变时模态振幅A1,6、A2,6的幅频特性曲线Fig.5 Amplitude frequency characteristic curve of A1,6 and A2,6 modal amplitudes when damping coefficient c change

由图5可看出，模态响应振幅在阻尼系数c变大后变化不大，响应曲线略向左移动，共振区间变化不大。随着阻尼系数的增大，从刚开始的重合到逐渐偏离，但偏离的距离较小，一阶模态对应的半椭圆形解分支从刚开始的分离到逐渐重合，二阶模态对应的封闭环解略变小。因此，改变阻尼系数大小(即改变阻尼项)，系统的响应幅值变化不大，故系统的非线性动力学行为对阻尼不敏感，主要原因在于柔轮圆柱壳的质量较小、弹性模量较大。于是，在设计柔轮参数与研究柔轮的非线性振动特性时，阻尼可以忽略不计。

4.3 初相角对模态振幅幅频特性的影响

选取参数为ε=0.01、c=12.25 Nsm-3、ω1=1 082.92 Hz、ω2=1 086.09 Hz、F(t)=20 N，根据式(11)，初相角选取γ=0、γ=π/2，绘制出在不同初相角γ下系统模态振幅A1,6、A2,6稳态解在频率比σ2/ω1变化下的幅频特性曲线(广义坐标下)，如图6所示。

由图6可看出，在初相角变化时，两阶模态的共振区间变化较大，响应振幅幅值变化较小。在初相角γ=π/2时，相比γ=0时的响应，两阶模态的共振区间均变小，一阶模态的响应曲线向右移动，二阶模态的响应曲线向左移动；由于二阶模态的响应曲线左移，使得二阶模态的半椭圆形解分支与封闭环解汇合，在区间σ2/ω1=4.1～7.2内，系统振动特性较为复杂；在区间σ2/ω1>4后，两阶模态的响应幅值在不同解分支上不停地跳跃，系统的跳跃现象比较明显。

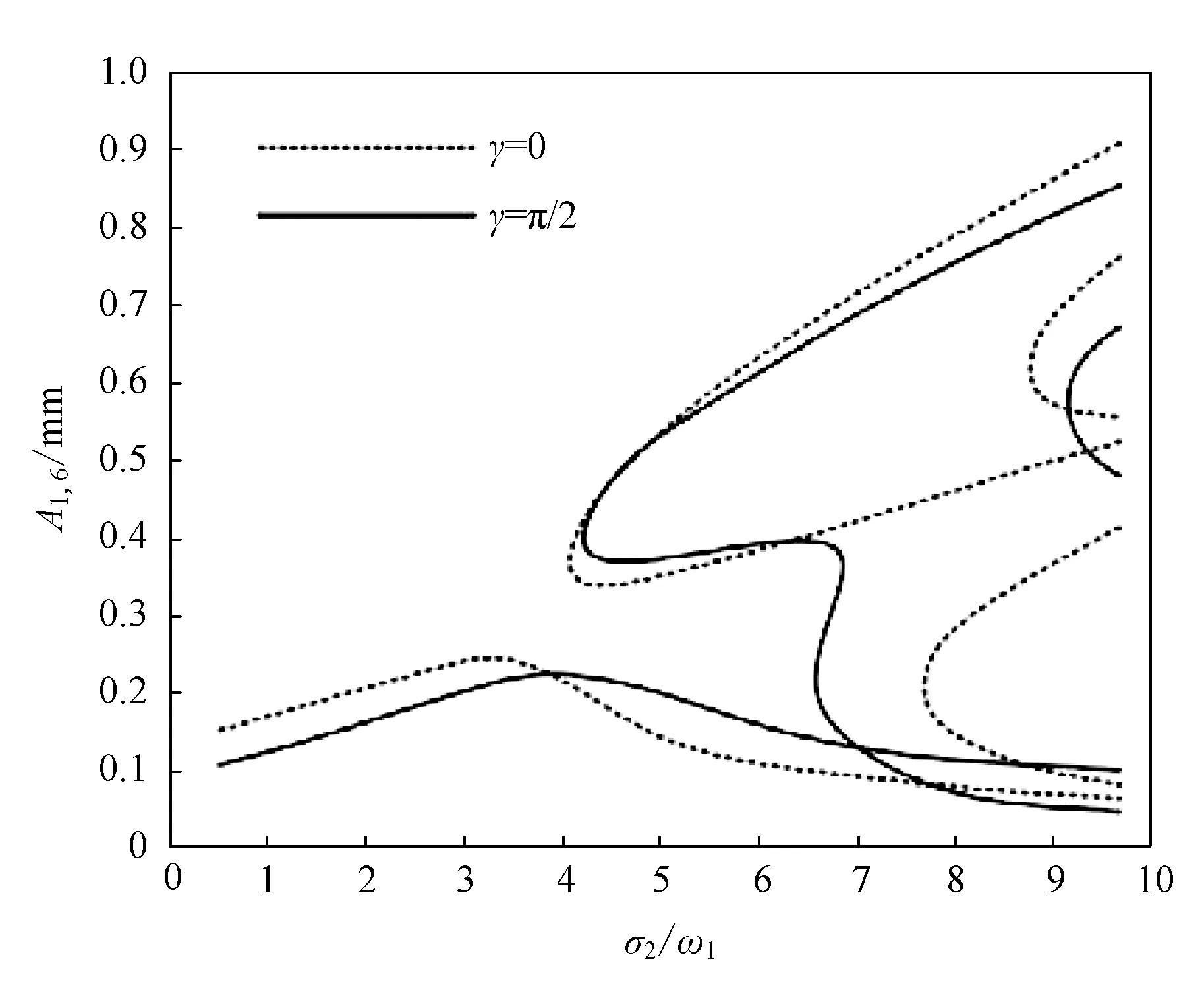
图6 不同初相角γ下模态振幅A1,6、A2,6的幅频特性曲线Fig.6 Amplitude frequency characteristic curve of A1,6 and A2,6 modal amplitudes under different initial phase anglesr

5 结论

本文将电磁谐波活齿传动系统激波器中的柔轮近似为一端固定、一端自由的薄壁圆柱壳，将动态特性模量、阻尼、柔轮的几何非线性等因素考虑进去，建立柔轮的非线性振动微分方程，将其离散化后得到模态方程组，利用多尺度法求解能反应系统1∶1内共振现象的主共振，研究存在1∶1内共振时系统的能量转换过程，分析了小参数、阻尼系数、初相角改变时对系统非线性振动特性的影响程度，结果表明：

1)两阶模态的固有频率很接近，柔轮在受到一阶固有频率附近电磁激励力的激励时，两阶模态之间的耦合特性较为强烈，两模态之间的能量传递迅速，彼此相互影响约束，产生了1∶1内共振，表明内共振下系统的模态耦合特性。

2)考虑存在1∶1内共振的电磁谐波活齿传动系统柔轮主共振的幅频特性曲线表现出软特性，共振区间存在多个解分支，在不同的解支中，响应多次跳跃。

3)小参数越大，系统响应曲线越复杂，响应振幅值越大，系统非线性越强；小参数越小，系统响应曲线越平滑，系统非线性越弱并接近线性，说明能量在模态间传递平稳。

4)系统阻尼系数变化后，响应幅值变化不大，系统的非线性动力学行为对阻尼不敏感。于是，研究柔轮的非线性振动特性时，阻尼可以忽略不计。

5)改变初相角大小，两阶模态响应曲线的共振区间变化较大，响应振幅幅值变化较小。因此，初相角的不同选取，对系统的非线性动力学行为影响较大。