组间零相关区周期互补序列集的构造
2021-12-10白子祎
白子祎,刘 凯,*
(1.燕山大学信息科学与工程学院,河北 秦皇岛066004;2.燕山大学河北省信息传输与信号处理重点实验室,河北 秦皇岛066004)
0 引言
随着准同步码分多址(quasi-synchronous code division multiple access,QS-CDMA)在卫星通信中的商用,学者们提出零相关区(zero correlation zone,ZCZ)序列集的概念[1-5]。为了得到更多满足具有良好系统性能的序列,学者们将ZCZ的概念和互补集两者结合,提出并构造了ZCZ互补序列集[6-8]。5G技术将蜂窝通信细化为大量的区组通信,因此具有组间良好相关性的序列设计受到了学者们的关注。目前组间互补(inter-group complementary,IGC)序列集的概念是组内具有ZCZ相关特性和组间具有理想的互相关特性。现有的IGC序列集构造方法并不多,文献[9]首次基于完备互补码和正交码构造了非周期IGC序列集,并应用到CDMA系统,相对于传统地址码具有更低的误码率,但ZCZ的长度固定于原始完备互补码的子序列长度,这限制了IGC序列集的数量。文献[10]利用周期互补序列集(periodic complementary sequence set,PCSS)和移位交织提出了改进的周期IGC序列集的构造方法,利于灵活选择ZCZ的长度,但是完备互补码数量的限制阻碍了IGC序列的应用。文献[11]基于零相关区周期互补序列集(zero correlation zone periodic complementary sequence set,Z-PCSS)和最佳周期互相关(perfect periodic cross-correlation,PPCC)序列集构造了周期IGC序列集,其ZCZ的长度灵活可变,但IGC序列集的组数取决于PPCC序列集中子序列的数量,文献[12]利用PCSS和正交矩阵也构造了周期IGC序列集,但其组数受限于互补序列集中子序列的数量。文献[13]基于正交矩阵构造了非周期IGC序列集,通过减少ZCZ的长度,增加IGC序列集的组数。目前文献中针对组间特性的扩频码设计方法并不多,数量也较少,因此研究更多的具有组间特性的序列具有实际意义。
本文提出了组间零相关区互补(intergroup zero correlation zone complementary,IGZC)序列集的定义,该序列集的组内和组间都具有ZCZ的性质,其中组内ZCZ的长度为Z1,组间ZCZ的长度为Z2。当Z1≠Z2且Z2=L时,IGZC就成为IGC,因此,IGC是IGZC的组间ZCZ长为L的情况。文中利用ZCZ序列集和整数集构造了一类Z1=Z2的IGZC,其中ZCZ长度,集合的组数可以灵活选择。当Z1=Z2=Z=L时,即为组内和组间都具有理想的相关特性的互补序列集合,是周期IGZC序列集的一种特殊情况。对IGZC构造方法的探索可为多小区不同时延信道模型提供更多的地址码选择,对消除多小区用户之间的信息干扰具有一定意义。
1 基本定义
定义1两个长度为L的复数序列a和b,分别表示为a=(a(t)|0≤t (1) 其中,b*(t)为b(t)的复共轭。当a=b时,上述定义为周期自相关函数,可写为Ra(τ)。 定义2设U={uk|0≤k (2) 引理1[14]对于任意一个参数为ZCZ(L,K,Z)的ZCZ周期序列集,满足以下理论界 K≤⎣L/Z」, (3) 其中,⎣L/Z」表示小于或等于L/Z的最大的整数。当K=⎣L/Z」时,称序列集U为最佳的,当K=⎣L/Z」-1时,称序列集U为几乎最佳的。 M≤N⎣L/Z」, (5) 其中,⎣L/Z」表示小于或等于L/Z的最大整数。当M=N⎣L/Z」时,称序列集cg为最佳的,当M=N⎣L/Z」-1时,称序列集cg为几乎最佳的。 GM≤N⎣L/Z」, (7) 其中⎣L/Z」表示小于或等于L/Z的最大的整数。当GM=N⎣L/Z」时,称U为最佳IGZC序列集,当GM=N⎣L/Z」-1时,称U为几乎最佳IGZC序列集。 定义5[15]对于任意的长度为L的复值序列a,可以定义以下映射作为a的线性相位变换,即 (8) 引理4[15]对于两个长度为L的复值序列a和b,如果q|L,其中q为模值,有 本文利用以下三个步骤构造IGZC序列集。 步骤1选取基序列集。任意选取一个ZCZ周期序列集,参数为ZCZ(L,K,Z),即U={uk|0≤k 步骤2将基序列集分为多个子序列集。选取用户数M,0 (10) (11) 其中,0≤m (12) 需分四种情况分析: 由以上分析可得 (13) 推论1当K为大于1的整数,且M=1时,C={cg|0≤g 证明与定理1的证明同理,这里不再赘述。 例1设q=4,M=2,选取一个含有3个整数的集合D={1,2,4}和一个参数为ZCZ(16,4,3)的二元ZCZ周期序列集U={uk,0≤k<3}作为基序列集,其中 u0=(1,1,-1,1,1,1,-1,1,-1,-1,-1,1,-1,-1,-1,1), u1=(-1,-1,1,-1,1,1,-1,1,1,1,1,-1,-1,-1,-1,1), u2=(1,-1,-1,-1,1,-1,-1,-1,-1,1,-1,-1,-1,1,-1,-1) u3=(-1,1,1,1,1,-1,-1,-1,1,-1,1,1,-1,1,-1,-1)。 令K=4,G=⎣K/M」=2,可以将U分为U0和U1,存在以下3种分组情况: 每种分组情况可以得到一种IGZC序列集,下面以情况1和情况2为例求序列集C={cg|0≤g<2}: 图1 c0的周期自相关函数R00和R01Fig.1 Periodic auto-correlation functions R00 and R01of c0 图2 c1的周期自相关函数R10和R11Fig.2 Periodic auto-correlation functions R10 and R11 of c1 图3 组内周期互相关函数R0和R1Fig.3 Periodic cross-correlation functions R0and R1 within c0and c1 图与c1内序列的周期互相关函数H00和H01Fig.4 Periodic cross-correlation function H00 and H01 of and the sequences of c1 在理论界方面,由于基序列集U的理论界为K≤L/Z,又因为GM≤K,那么GM≤L/Z,可以推导出GM 表1 周期IGC序列集参数对比Tab.1 Parameter comparison of periodic IGC sequences sets 从表1显示,文献[10]构造的IGC序列集虽然达到了理论界,但其数量受限于PCSS的数量,因此得到的可用的IGC序列集数量很少,而文献[11]中的构造方法虽然提高了IGC序列集的数量,但其组数取决于PPCC序列集中子序列的数量,需要通过改变基序列集来得到更多的IGC序列集。文献[12]构造的IGC序列集需要在一定条件下实现理论界,且其组数受限于互补序列集中子序列的数量。相比上述文献,定理1的构造方法中应用ZCZ周期序列集作为基序列集,依据已有文献,这类序列集数量非常丰富,通过选择不同参数的基序列集,很容易获得IGZC所需的ZCZ长度。此外,在IGZC的构造中,用户数M可以根据实际情况进行设定,在不改变基序列集的情况下,根据M的灵活选择可获得不同分组,从而得到多个IGZC序列集,如例1所示。移位整数集中参数数量代表着信道载波数,整数集的大小可根据实际需求灵活选择。尽管定理1构造的IGZC序列集不能达到理论界,但构造结果丰富,且参数选取依据实际通信需求可灵活选择,具有实用性。 本文基于ZCZ序列集和整数集提出了Z1=Z2情况下的周期IGZC序列集的构造方法。构造的周期IGZC序列集在组内和组间的零相关区内都具有理想的相关特性。通过选择不同参数的基序列集能灵活地选择ZCZ的长度与集合的组数,通过改变整数集中整数的个数,集合的大小也能灵活选择,相比于文献中构造的IGC序列集,可得到数量更多的IGZC序列集。IGZC序列集中Z1≠Z2的情况有待进一步研究,随着IGZC序列的深入设计将得到更多适合多小区通信的扩频码。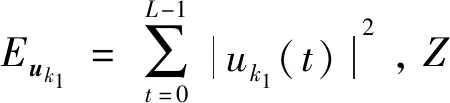
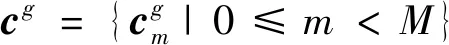
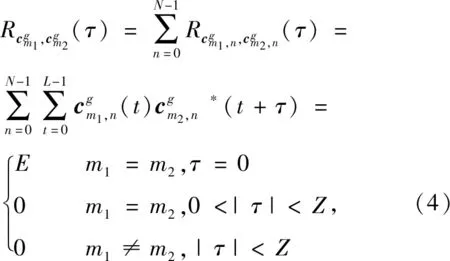
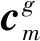
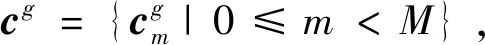
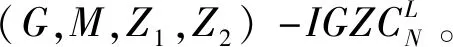
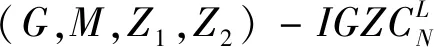
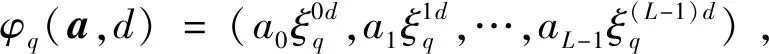
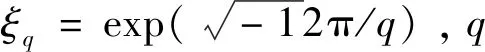
2 组间零相关区互补序列集的构造

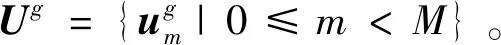
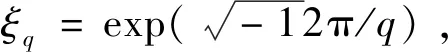

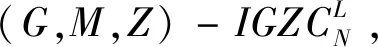
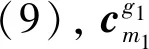
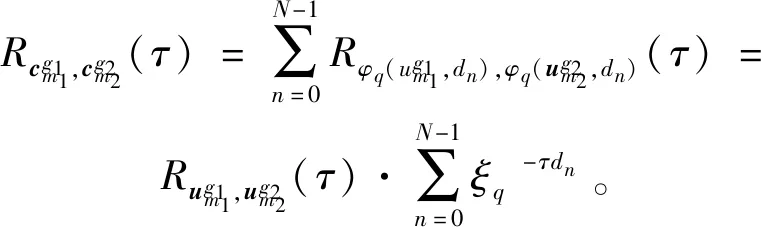
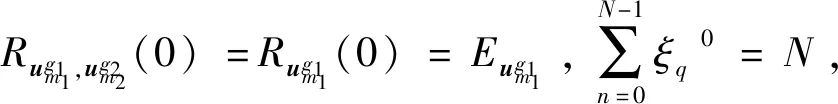

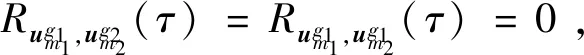
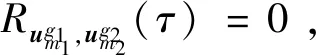
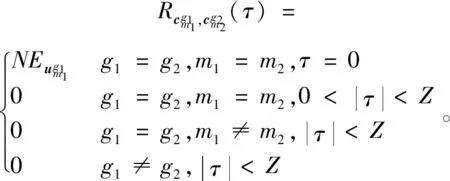
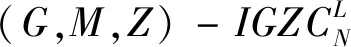
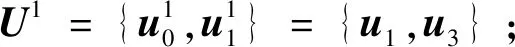

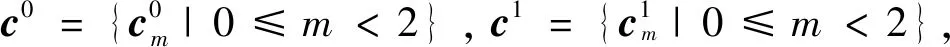
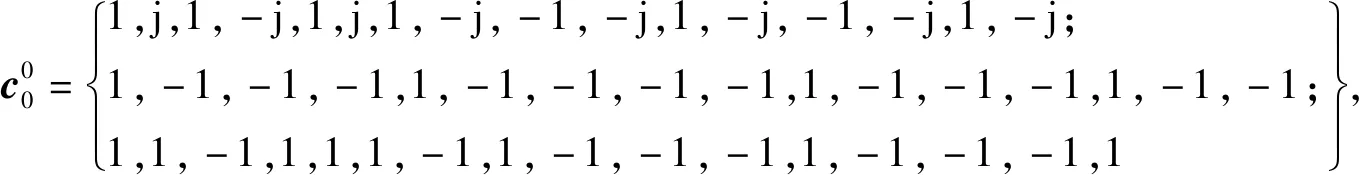

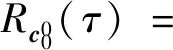
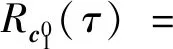
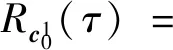
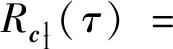
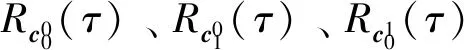

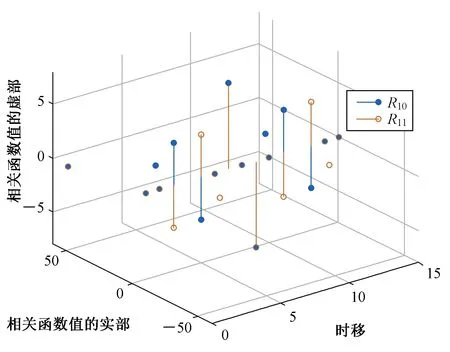
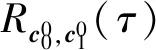
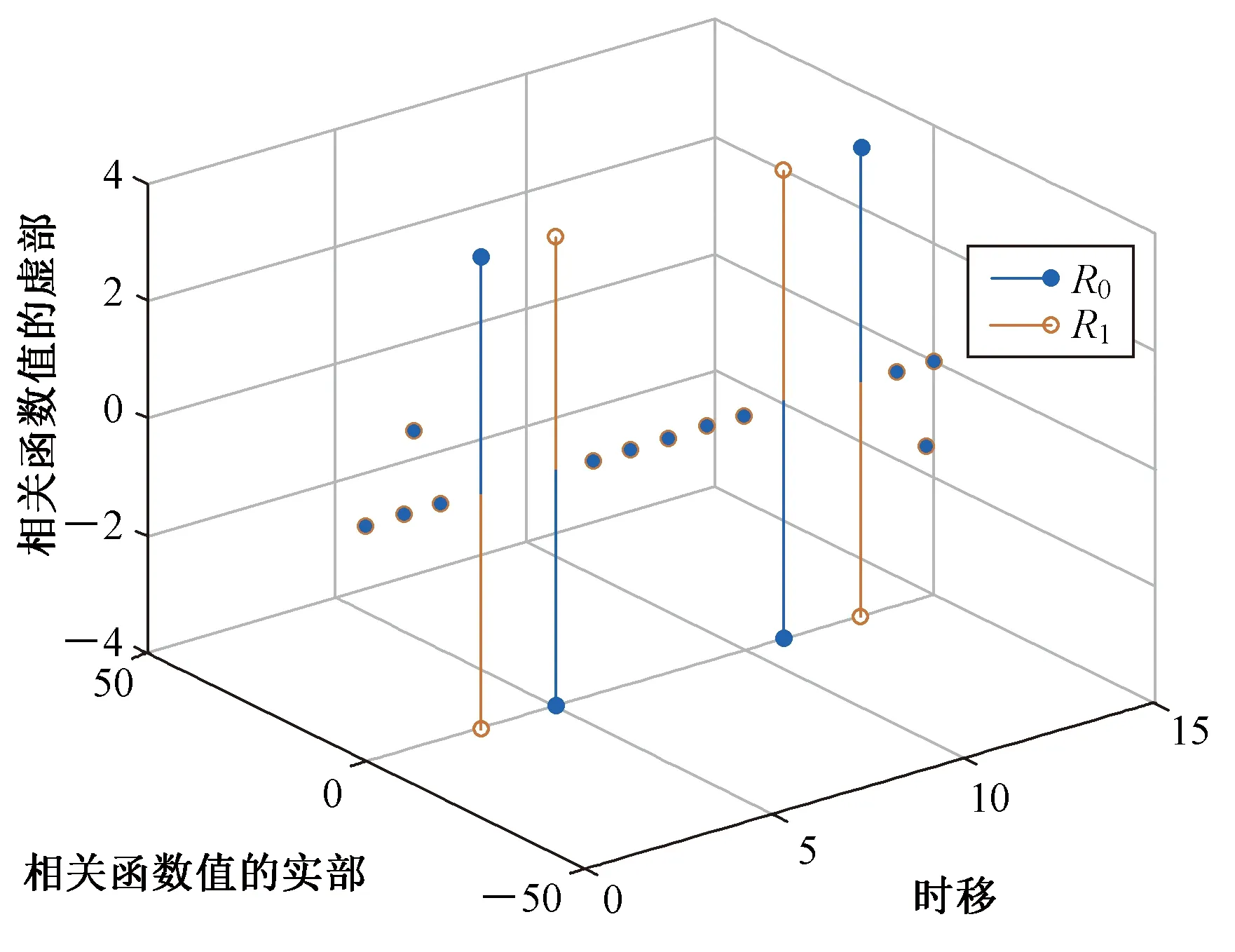
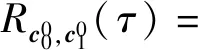

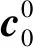

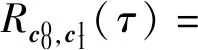
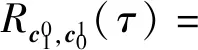
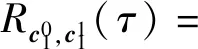

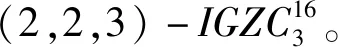
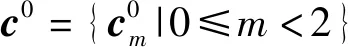
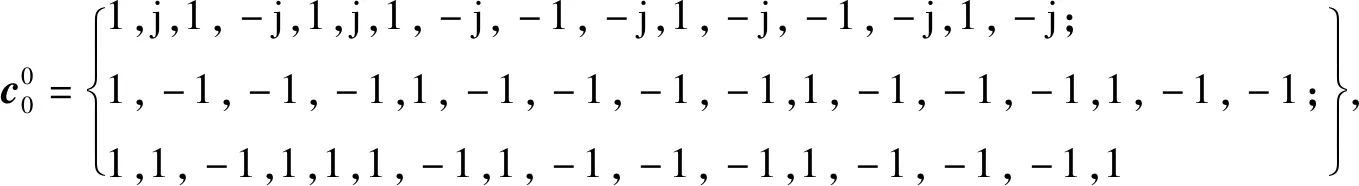
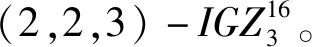
3 性能分析

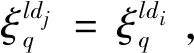

4 结论
