地铁列车曲线运行引起学校建筑物振动响应分析

夏志强,凌可胜,董克胜,徐小扣,沈 威,方火浪

(1.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122;2.杭州未来科技城建设有限公司,浙江 杭州 310012;3.浙江大学 建筑工程学院,浙江 杭州 310058)

0 引言

本文以杭州市地铁3号线曲线地段的某中学建设工程为研究对象,利用有限元软件ABAQUS和MIDAS GTS/NX,分别建立车辆-轨道系统耦合动力模型和隧道-土-桩-建筑物系统三维有限元动力模型,对地铁列车运行引起的新建学校建筑物振动响应进行计算与分析,并根据相关环境振动控制标准对建筑物的振动舒适性进行评价。

1 分析方法与计算模型

1.1 分析方法

地铁列车引起的环境振动是一个复杂的综合性问题,涉及车辆、轨道、隧道、地层、基础和建筑物的动力相互作用。为了简化该问题的复杂性,把整个动力系统分为车辆-轨道耦合动力子系统和隧道-土-基础-建筑物耦合动力子系统,两个子系统通过轨道支点(扣件)连接。采用车辆-轨道耦合动力子系统求解轨道支点力,将其应用于轨道与隧道的接触表面作为动力激励,计算隧道-土-基础-建筑物耦合子系统的振动响应。

1.2 车辆-整体道床轨道系统耦合动力模型

根据车辆-轨道耦合动力学理论,建立了图1所示的车辆-普通整体道床轨道系统的竖向相互作用动力模型。该模型考虑了车辆、钢轨、扣件和基础之间的相互作用,包括车辆子模型和轨道结构子模型。通过输入轮轨接触处的轨道随机不平顺,利用赫兹非线性接触关系得到轮轨之间的相互作用力,使车辆和轨道系统发生振动,然后利用轮轨之间的位移协调和力平衡条件,通过迭代计算,实现车辆与轨道的耦合,得到系统的动力响应。

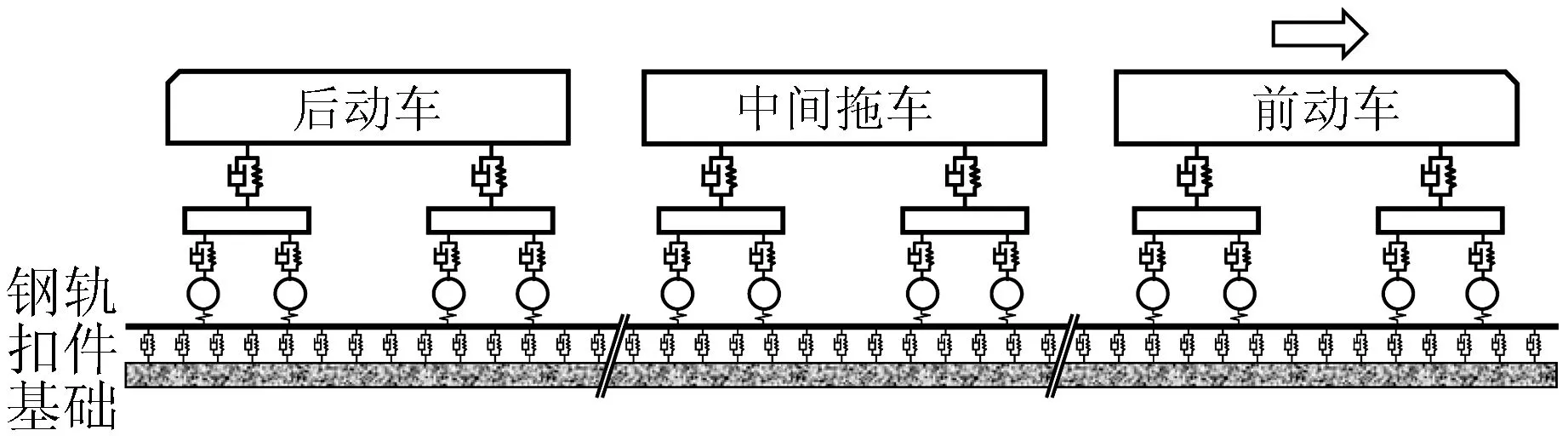
图1 车辆-普通整体道床轨道系统竖向耦合动力模型Fig.1 A vertical coupling dynamic model of vehiclecommon monolithic track system

杭州市地铁3号线地铁列车采用AH型6车编组(2动4拖),设计最大时速为80 km/h,轨道扣件纵向间距为0.6 m。

1.3 隧道-土-桩-建筑物有限元模型

采用有限元软件MIDAS GTS/NX建立了双孔平行曲线盾构隧道-土-桩-建筑物三维有限元精细化模型。图2(a)为整体有限元模型,图2(b)为隧道、桩和建筑物有限元模型,土体采用三维实体单元,楼板、地下室外墙、底板、剪力墙和隧道管片采用板单元,钢筋混凝土柱、梁和桩基础采用梁单元。在网格生成过程中考虑了地铁振动主频带、土层和结构的剪切波速以及单元尺寸对波动的影响,控制了各类材料的单元最大尺寸,所建整体有限元模型共741 327个节点,1 289 042个单元。为了尽量降低模型边界反射波对计算结果的影响,采用刘晶波等[19]的三维等效黏弹性边界,在整体模型的4个侧向边界和底部边界上设置切向和法向的弹簧-阻尼单元。场地土和建筑物的物理力学参数由岩土工程勘察报告、现场波速测试结果以及地铁与建筑物设计资料确定,计算用的材料参数列于表1。综合考虑有限元模型的竖向自振频率和地铁列车运行产生的优势频段(1～80 Hz),选取计算Rayleigh阻尼系数α和β的两个频率为5 Hz和80 Hz,整体有限元模型的系统阻尼比取0.03(小应变时的土体阻尼比为0.01～0.05,钢筋混凝土阻尼比为0.02～0.05),计算得到Rayleigh阻尼系数α=1.773,β=1.12×10-4。图3为阻尼比和频率之间的关系。可以看出,在优势频段,按Rayleigh公式计算得到的阻尼比在0.015～0.03的合理范围内。

图2 隧道-土-桩-建筑物系统有限元模型Fig.2 Finite element model of tunnel-soil-pile-building system

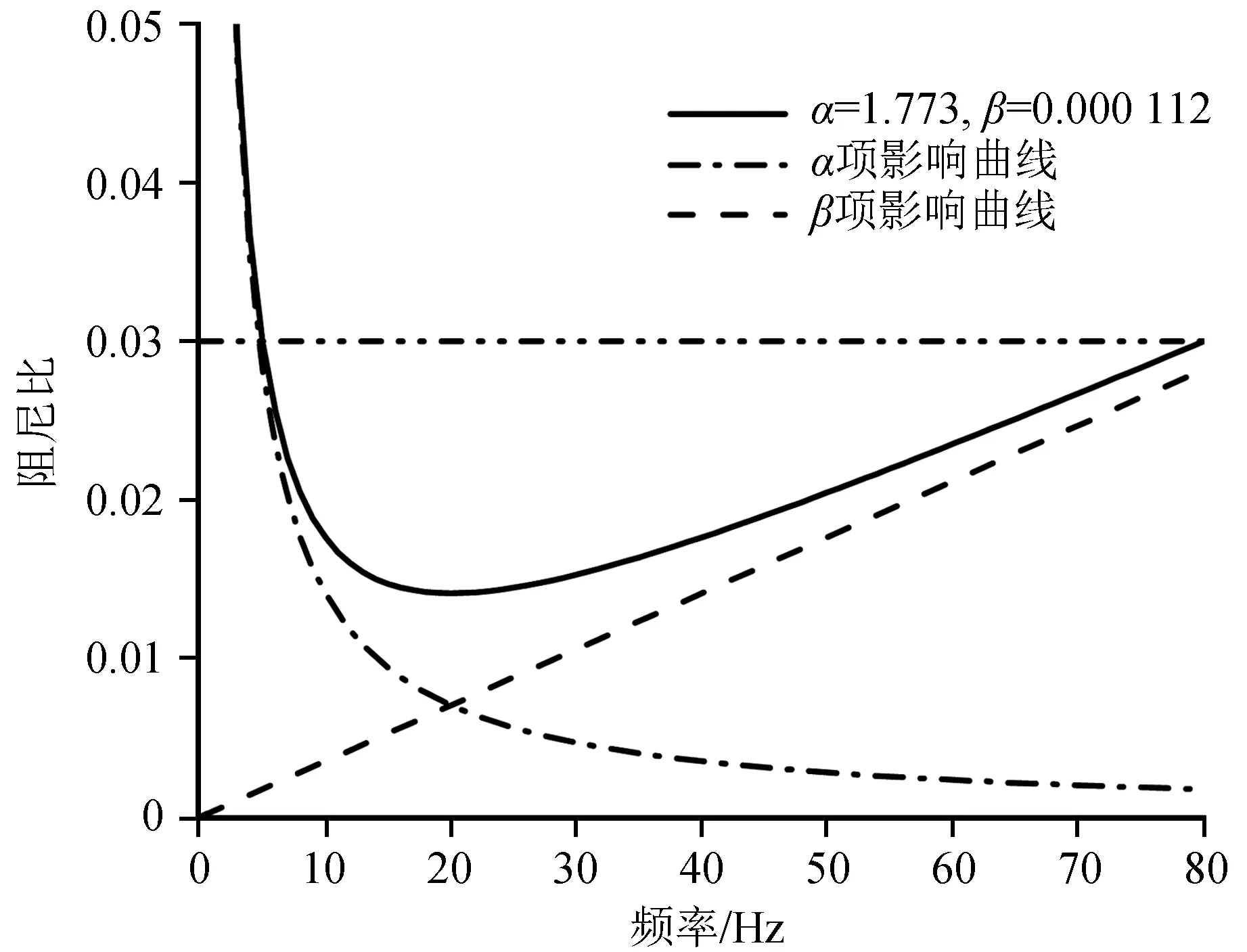
图3 阻尼比与频率的关系Fig.3 Relation of damping ratio and frequency

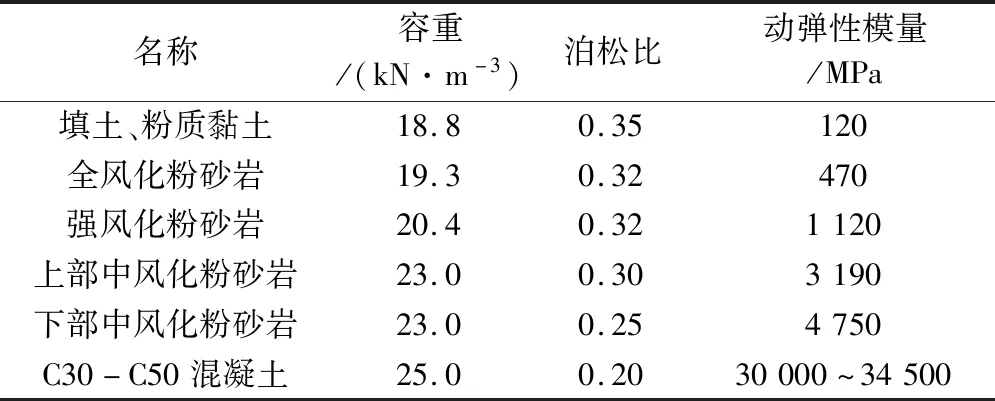
表1 材料参数Table 1 Material parameters

2 车辆-整体道床轨道系统耦合动力分析

图4是根据美国六级高低不平顺谱计算的轨道高低不平顺空间样本。利用有限元软件ABAQUS计算了在美国六级高低不平顺谱条件下的轨道动力响应,获得了普通整体道床轨道的振动源强。考虑到计算精度和列车长度,时间步长取0.002 s,总时间取11.5 s。图5为钢轨加速度、钢轨位移、轮轨接触力和扣件支点力的时程曲线。可以看出,当六节车体依次经过轨道观测点时,观测点处的加速度、位移和支点力大幅度增加,最大加速度约为40 m/s2,最大动支点力约为30 kN。并且由于普通整体道床轨道的刚度较大,加速度、位移、接触力和支点力响应的高频成分都比较丰富。

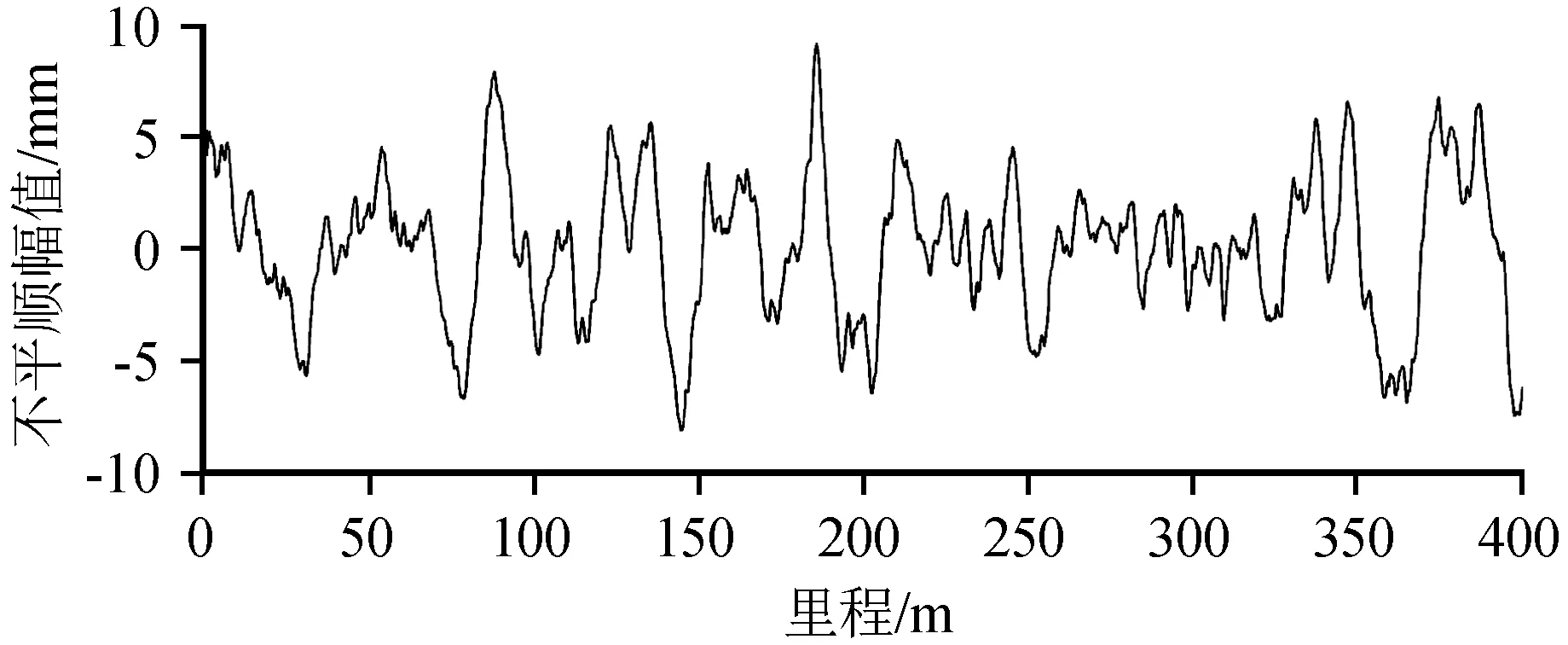
图4 轨道高低不平顺空间样本Fig.4 Space sample of track height irregularity

3 隧道-土-桩-建筑物系统有限元动力分析

考虑到上下行列车同时运行对地基和建筑物的振动影响较大,将列车荷载施加在上下行轨道的相应节点上。首先,对图5(d)的扣件支点力时程曲线进行时间轴左移,并减去静态支点力,得到隧道入口节点处的列车动荷载时程曲线。然后,根据扣件支点间距和行车速度对其进行延时处理,得到其他轨道相应节点的列车动荷载时程曲线。综合考虑计算精度、计算机容量和隧道长度,时间步长取0.005 s,总时间取24 s。利用有限元软件MIDAS GTS/NX计算了隧道-土-桩-建筑物系统的振动响应,主要结果如下。

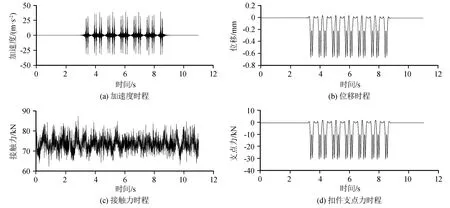
图5 钢轨竖向加速度、位移、轮轨接触力和扣件支点力的时程曲线Fig.5 Time history curves of vertical acceleration and displacement of rail,wheel rail contact force and fastener fulcrum force

3.1 振动加速度峰值分布特性

图6为整体地层沿坐标轴正方向各加速度分量的峰值分布。可以看出,总加速度、X向加速度、Y向加速度和Z向加速度的最大值分别为1.63×10-1m/s2、2.71×10-2m/s2、2.77×10-2m/s2和1.62×10-1m/s2;Z向最大加速度明显大于X向和Y向的最大加速度,Y向最大加速度略大于X向最大加速度。最大值发生在隧道所在的上部中风化层。地表层(填土、粉质黏土、全风化层和强风化层)总加速度、X向加速度、Y向加速度和Z向加速度的最大值分别为2.20×10-2m/s2、1.93×10-2m/s2、1.52×10-2m/s2和1.76×10-2m/s2。从地面峰值加速度的分布特征看,图6(a)与(d)、图6(b)与(c)基本相似,说明总加速度主要来自Z向分量,X向和Y向加速度峰值及其分布特征比较接近。比较正负方向对应分量的加速度分布可以看出,两者基本一致,说明正负向加速度峰值基本相同(限于篇幅,省略了整体地层沿坐标轴负方向各加速度分量的峰值分布图)。地面加速度随着距隧道中心线距离的增加而逐渐衰减,Z向加速度的衰减速度快于X向和Y向加速度。

中药方剂通过其多种成分作用于多种靶点，在疾病发生发展的关键生物学过程中起重要的作用。由于生物信息学的快速发展，网络药理学方法已成为一种高效、系统地揭示中药方剂分子机制的新手段[10-11]。网络药理学研究药物、靶标和疾病之间的关系，并通过系统的思想展示药物-靶标网络，将相互作用关系可视化为网络模型，并从整体的角度研究药物对生物网络的影响[12]。因此，本研究采用网络药理学方法，探讨钩藤散对AD的影响及其作用机制，为AD的临床治疗提供有价值的信息。

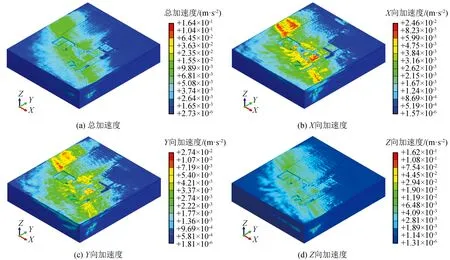
图6 整体地层加速度峰值分布Fig.6 Peak distributions of whole stratum accelerations

图7为建筑物沿坐标轴正方向各加速度分量的峰值分布。可以看出,总加速度、X向加速度、Y向加速度和Z向加速度的最大值分别为7.63×10-2m/s2、2.11×10-2m/s2、1.98×10-2m/s2和7.60×10-2m/s2;Z向最大加速度明显大于X向和Y向的最大加速度,Y向最大加速度大于X向最大加速度。从建筑物峰值加速度的分布特征看,图7(a)与(d)、图7(b)与(c)比较相似,说明总加速度主要来自Z向分量。比较正负方向对应分量的加速度分布可以看出,两者基本一致,说明正负向加速度峰值基本相同(限于篇幅,省略了建筑物沿坐标轴负方向各加速度分量的峰值分布图)。由于地铁穿越综合楼下方的地层,综合楼的峰值加速度大于图书馆和教学楼的峰值加速度。

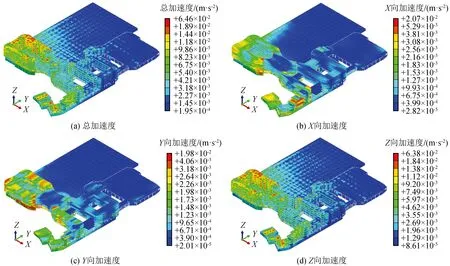
图7 建筑物加速度峰值分布Fig.7 Peak acceleration distribution of the building

图8为整体地层沿坐标轴正、负方向总位移的峰值分布。从图中可以看出,正、负方向总位移的最大值分别为5.21×10-6m和2.87×10-5m,地层沿坐标轴负方向位移大于正方向位移,隧道上方地面位移较大。图9为建筑物沿坐标轴正、负方向总位移的峰值分布。从图中可以看出,正、负方向总位移的最大值分别为6.04×10-6m和1.74×10-5m,建筑物沿坐标轴负方向位移大于正方向位移,综合楼和图书馆的位移较大。上述结果表明,地铁运行产生的地层和建筑物位移均很小。

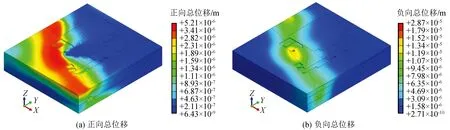
图8 整体地层位移峰值分布Fig.8 Peak displacement distribution of the whole stratum

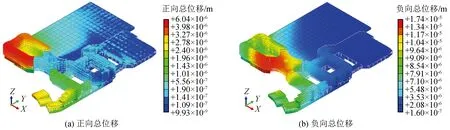
图9 建筑物位移峰值分布Fig.9 Peak displacement distribution of the building

3.2 建筑物楼层加速度时程曲线

图10为综合楼各楼层最大加速度节点的竖向加速度时程曲线。可以看出,楼层2～楼层4的加速度波形特征比较相似,楼层5和屋顶的加速度波形特征比较相似,楼层4的峰值加速度最大,楼层2的峰值加速度最小。

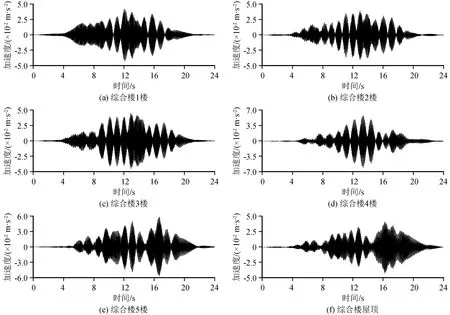
图10 综合楼各楼层竖向加速度时程曲线Fig.10 Vertical acceleration time history curves of complex building floors

图11为图书馆各楼层最大加速度节点的竖向加速度时程曲线。可以看出,楼层4和楼层5的加速度波形特征比较相似,屋顶的峰值加速度最大,楼层1的峰值加速度最小,楼层3～楼层5的峰值加速度比较接近。

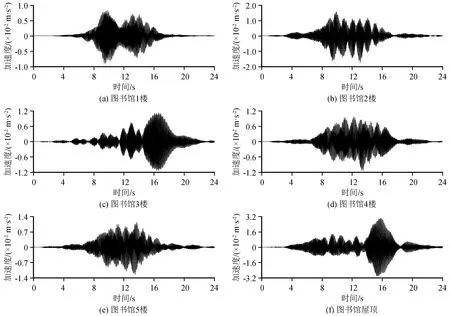
图11 图书馆各楼层竖向加速度时程曲线Fig.11 Vertical acceleration time history curves of library floors

图12为教学楼各楼层最大加速度节点的竖向加速度时程曲线。可以看出,楼层2和楼层3的加速度波形特征比较相似,楼层3的峰值加速度最大,楼层1的峰值加速度最小,楼层2、楼层4和屋顶的峰值加速度比较接近。

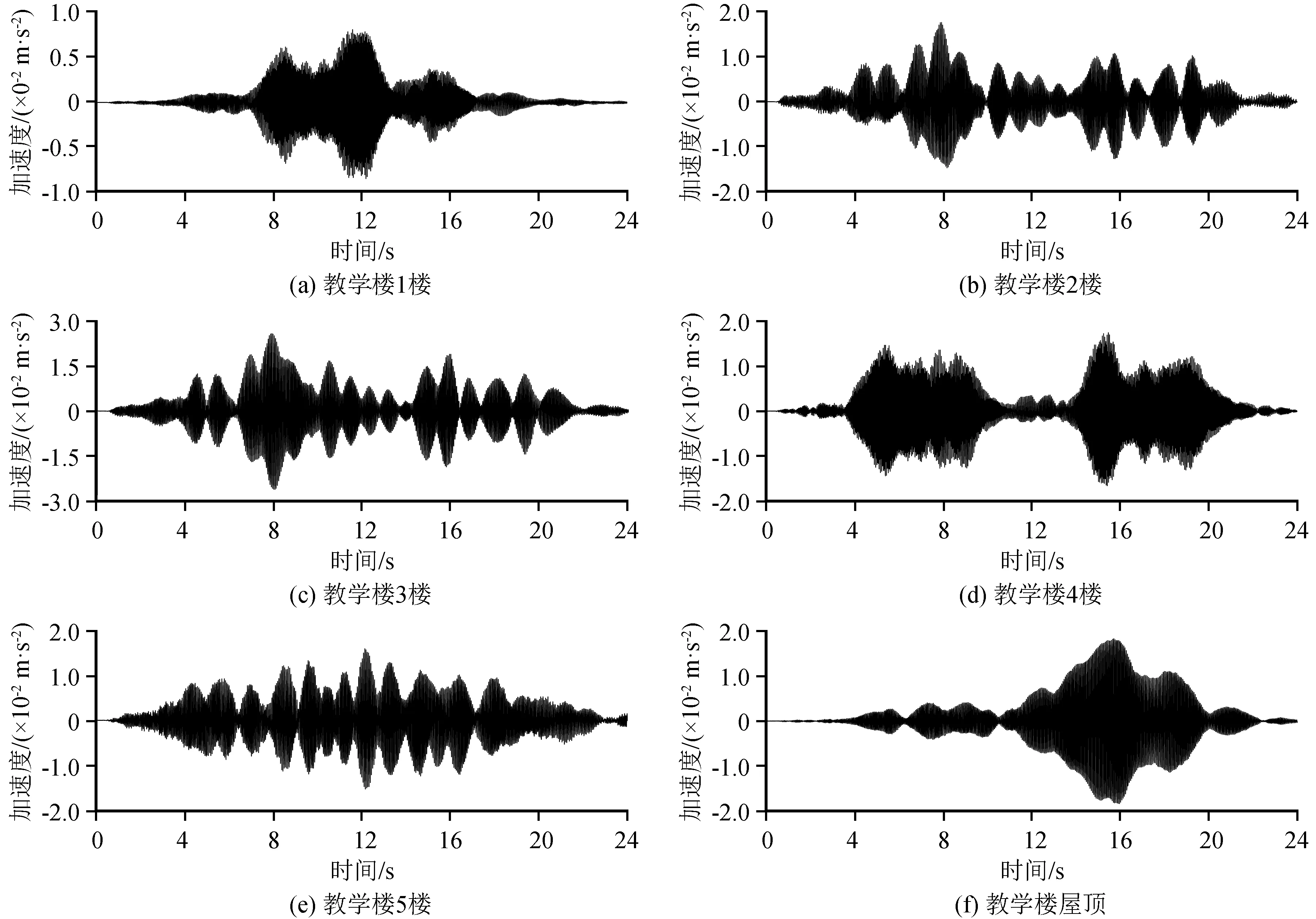
图12 教学楼各楼层竖向加速度时程曲线Fig.12 Vertical acceleration time history curves of teaching building floors

3.3 建筑物楼层竖向振动加速度级分频特性

根据各楼层最大加速度节点的竖向加速度时程曲线,将其进行频域分析,转化为1/3倍频程振动加速度级,定义为:

VAL=20lg(arms/a0)+C

(1)

式中:VAL为频率计权振动加速度级(dB);arms为加速度有效值(m/s2);a0为基准加速度(=10-6m/s2);C为中心频率处的计权因子(dB)。

图13为综合楼、图书馆和教学楼各楼层最大加速度节点的计权竖向振动加速度级1/3倍频程谱。可以看出,3建筑物各楼层的频率分布特征基本相似,主频均位于中心频率16、20和40 Hz附近。综合楼的最大竖向振动加速度级发生在屋顶,其值为80.3 dB。图书馆的最大竖向振动加速度级发生在屋顶,其值为74.6 dB。教学楼的最大竖向振动加速度级发生在楼层3,其值为73.9 dB。

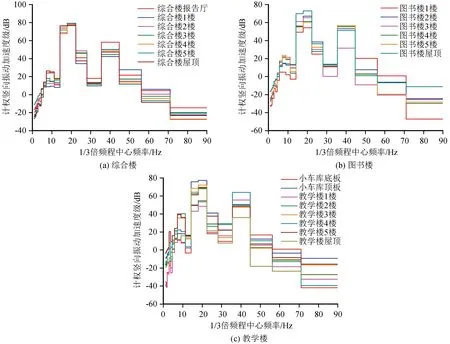
图13 建筑物各楼层计权竖向振动加速度级1/3倍频程谱Fig.13 1/3 octave spectra of weighted vertical vibration acceleration level for building floors

3.4 基于环境振动控制标准的振动舒适性评价

由于振动舒适性具有较强的主观性,不同控制指标的计算公式具有经验性。现行的用于评价轨道交通环境振动水平的标准主要为《城市区域环境振动标准(GB 10070—88)》[20],评价指标为按照全身振动不同频率计权因子修正后得到的计权竖向振动加速度级,即Z振级,定义为

(2)

式中:VLZ为Z振级(dB);VALi(i=1,2,…,n)为第i个中心频率处的计权振动加速度级(dB)。

根据《城市区域环境振动标准(GB 10070—88)》,取时间积分常数为1 s,重叠系数为3/4,将时程信号依次分为若干幅波形,对每一幅波形进行1/3 倍频程分析得到各个中心频率对应的分频振级。通过序贯计算可获得Z振级随时间的变化过程,即运行Z振级VLZ(t),最大Z振级即为列车通过时间内多个时段的Z 振级最大值。表2给出了建筑物各楼层的Z 振级最大值,结果表明大部分楼层的Z振级已超过该标准中关于城市轨道交通运行对文教类建筑产生振动白天不大于70 dB,夜间不大于67 dB的限值要求。

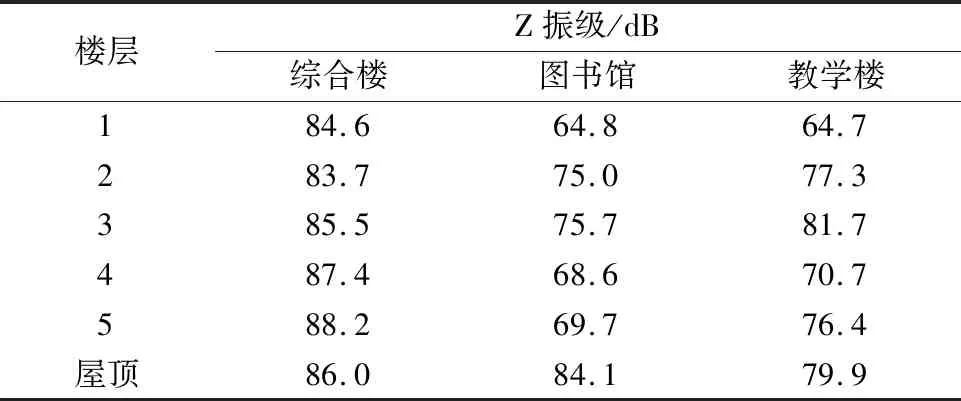
表2 建筑物各楼层Z振级最大值Table 2 Maximum values of Z vibration level for building floors

4 结语

针对杭州地铁3号线运营期间可能给某新建学校建筑带来的环境振动问题,利用有限元软件ABAQUS和MIDAS GTS/NX,分别对车辆-轨道系统竖向耦合模型和隧道-土-桩-建筑物系统三维有限元模型的振动响应进行了计算,研究了地铁振动波在地层中的传播规律和建筑物的振动响应特性,评价了建筑物的振动水平和振动舒适性,得出以下结论:

(1)当车辆通过时,普通整体道床轨道的加速度、位移和支点力响应均大幅增加。最大加速度约为40 m/s2,最大动支点力约为30 kN。由于轨道刚度较大,其加速度、位移、接触力和支点力响应的高频成分均比较丰富。

(2)地铁列车运行引起的地层振动以竖向为主,水平Y向振动略大于水平X向振动,正负向加速度峰值基本相同。地面加速度随着距隧道中心线距离的增加而逐渐衰减,Z向加速度的衰减速度快于X向和Y向加速度。

(3)地铁列车运行引起的建筑物振动以竖向为主,水平Y向振动略大于水平X向振动,正负向加速度峰值基本相同。各建筑物楼层的振动主频位于16～40 Hz。综合楼的峰值加速度大于图书馆和教学楼的峰值加速度,楼层峰值加速度与层高的关系随着建筑物的变化而变化。

(4)地铁列车运行引起的部分建筑物楼层的振动响应水平已超出了规范的限值要求,建议对地铁轨道或建筑物采取适当的减振措施。