基于协同惯量控制的双馈风机并网系统稳定性分析

胥心怡, 武家辉，姚磊，张强

(1.可再生能源发电与并网控制教育部工程研究中心(新疆大学),乌鲁木齐市 830047；2.国网新疆综合能源服务有限责任公司，乌鲁木齐市 830011)

0 引 言

目前风电接入比例越来越高，这使包括频率稳定在内的电力系统维持稳定性及安全性面临着巨大的挑战。双馈风力发电机(doubly-fed induction generator，DFIG)采用了矢量控制技术，具有功率解耦控制、最大风能跟踪、高风能利用率等优点，是风电市场的主流机型。DFIG因为其运行特性，没有常规机组所具备的惯性响应能力，因此风机在大规模并网后，使电力系统的惯性响应能力明显降低，同时也导致了含风电电力系统的惯性显著减弱。当电力系统遇到扰动时，频率不能够保持在规定的范围中波动，将会对系统整体的安全稳定性造成一定影响[1]。若内部存在的惯量过少，将加快系统频率跌落的速度。为了加强电网对风电的接纳能力，需对风电机组的控制模块或者控制方法做出改进，使其提供一定的惯量支撑。

在电力系统出现功率缺额情况下，频率最初的跌落速度以及频率跌落的最低值、维持的时间与电力系统暂态稳定的能力等一些关键因素和电力系统整体的惯性响应能力密不可分[2]。DFIG的机电解耦特性易造成系统整体等效惯量的降低和电网频率特性恶化等问题，这类问题能够通过虚拟惯量控制的方法来进行改善[3]。目前，对于提升存在风电接入的电力系统稳定性的方法已有一些研究。文献[4-5]把重点放在了讨论DFIG并网对整体惯量水平以及频率变化过程的影响，只从理论上分析了风电并网系统在虚拟惯量控制作用下的暂态稳定影响机理，没有考虑复杂故障情况时的影响。文献[6]提出一种能够提高系统虚拟惯量的自适应控制策略，但所采用的惯量控制方法使系统产生不同程度的振荡。文献[7]推导出虚拟同步发电机控制器参数与虚拟惯量之间的关系，所提出的协调控制方法受控制器参数影响较大。文献[8-9]中的虚拟惯量控制方法，着重研究了风电机组虚拟惯量控制参数的变化范围，但系统控制效果对参数要求较高，在实际运行中对维持系统频率稳定效果并不大。文献[10-11]提出的惯量控制策略能够有效提高电力系统频率的动态响应性能，使系统稳定性得到显著改善。上述文献的研究减少了大规模DFIG接入电网引起频率扰动的效果，但是上述文献都未对风机转子转速做出相应的优化。文献[12]利用控制风机的转子达到频率支撑的目的，并通过频率控制策略，得到最优的输出功率曲线。文献[13-14]表明了目前针对风电机组虚拟惯量控制方面的研究主要是通过风电机组转子动能提供惯性支撑，没有考虑采用协同控制的方法。文献[15-16]均提出采用协同控制策略在系统功率缺额时提供瞬时功率支撑并为电网提供较长时间的频率支撑。但没有具体讨论协同虚拟惯量控制技术在不同工况时对DFIG并网系统的影响。

针对DFIG并网系统的惯量特性，对基于DFIG转子转速控制和虚拟惯量控制协同控制下风电并网系统的出力变化展开分析。从DFIG的电磁转矩方程出发，考虑风机转子转速变化对系统惯量的影响，从理论上推导出有功控制的表达形式，控制风电中的虚拟惯量，搭建转子转速控制模块及虚拟惯量控制模块，并深入讨论在不同工况下协同惯量控制对含风电的电力系统中风电惯量支撑能力的影响。研究结果可以为含风电的电力系统稳定运行提供理论支撑。

1 DFIG的虚拟惯量特性

1.1 DFIG电磁转矩控制

在dq坐标下建立DFIG的暂态模型，ψsd、ψsq、ird、irq、ωr为状态变量。得到DFIG在dq坐标轴下的磁链方程：

(1)

式中：ψsd、ψsq为定子磁链的dq轴分量；ψrd、ψrq是转子磁链的dq轴分量；isd、isq为定子电流的dq轴分量；ird、irq为转子电流的dq轴分量；Lm表示定子绕组间的互感，也表示转子绕组间的互感；Ls表示定子绕组本身的自感；Lr表示转子绕组本身的自感[17]。此外，电压方程为：

(2)

式中：usd、usq为定子电压的dq轴分量；urd、urq表示转子电压的dq轴分量；Rs和Rr分别为定子和转子绕组各相电阻；ω1、ωs分别为发电机的同步角速度、转差角速度；p为微分算子。转矩方程为：

Te=npLm(isqird-irqisd)

(3)

式中：Te为电磁转矩；np为DFIG的极对数。

将式(1)代入式(2)简化后：

(4)

式中：us表示定子电压矢量的幅值。

结合式(2)得到电压方程：

(5)

DFIG选择定子磁链定向矢量控制后，其输出的有功功率与无功功率的表达式更加简洁，有利于对系统的精确计算，从而使变换器控制变得简单。定子磁链定向矢量控制是高性能调速方法，不易受到转子参数影响，但易受积分过程的影响，若控制目标为系统功率，控制系统的特性最佳[18]。采用该方法时，忽略定子电阻的电压，则磁链方程为：

(6)

式中：ψs表示风力发电机定子中含有的磁链幅值。

电流方程：

(7)

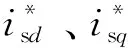
当定子输出的有功及无功保持一定时，令式(4)中微分项为0得到：

(8)

将电压方程、电流方程代入式(3)能够得到电磁转矩方程：

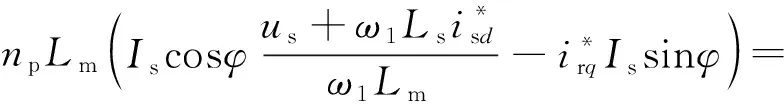
(9)

可以通过电磁转矩与q轴转子电流之间的关系，来改变风电机组的电磁转矩从而控制有功功率，实现虚拟惯量控制。

1.2 DFIG转子转速控制

DFIG的主要控制系统有转速控制模块、转子侧变换器控制模块和电网侧变换器控制模块。转速控制系统包括风机电磁转矩控制和桨矩角控制。发电机电磁转矩起到控制转子侧变换器和网侧无功功率的作用。

若某一时刻风速发生突变时，要改变转速参考值，选择忽略无功电压对系统的影响，转子电流有急剧的变化，可以得到与电磁转矩相关联的变换器电流内环控制模型[19]。该变换器的电流内环控制模型可简化成：

(10)

式中：Gq(s)为电机传递函数；τ为变换器惯性响应时间常数[20]；s表示复参数。

风电机组用改变转子转速的方式来改变输出功率，从而达到惯性响应的目的，电网频率变化过程中瞬时时刻的功率增量决定惯性响应的能力。DFIG转子转速控制是在电网频率波动的过程中，用改变双馈风力发电机的转子转速，控制发电机的输出功率，对含风电的电力系统进行暂态的功率支撑[21]。建立如图1所示的转子转速控制模块，图中：Tmax和Tmin分别为电磁转矩的最大值、最小值。

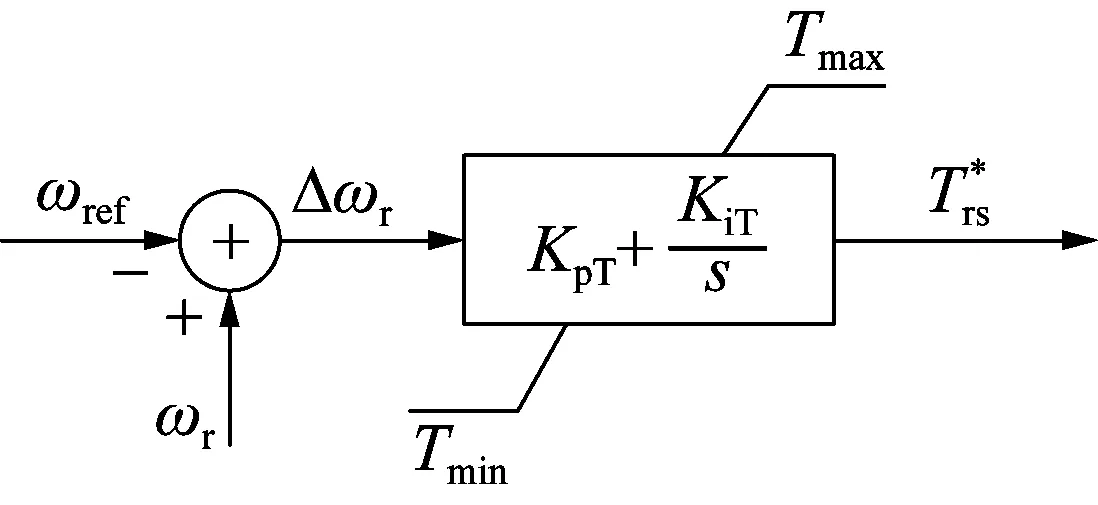
图1 转子转速控制模块Fig.1 Modules of rotor speed control

转子转速控制模型为：

(11)

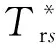
通过上述分析可知，双馈风力发电机的电磁功率会在系统出现故障的情况下有所降低，造成风电机组运行加速。由于双馈风力发电机的转子转速控制模块主要存在于转子侧的变换器中，当风机转子转速变化时，转子侧变换器会快速动作，因此通过控制转子转速来控制输出电磁转矩的变化，实现对有功功率的控制。从而得出，利用DFIG的转速特性可以达到调整双馈风力发电机输出有功功率的目的，对外表现出惯量特性，有益于提高电网的暂态性能，进而提高惯性响应能力[22]。

随着风电渗透率的增加，在无虚拟惯性响应状态下，含风电的电力系统的惯性响应能力逐渐降低；当风电伴随虚拟惯性响应时，含风电的电力系统频率变化率明显降低，机组转子转速降低，释放动能，系统惯性时间会短暂增加，惯性响应能力有所提升，给DFIG并网提供惯量支撑。

2 基于协同惯量控制的DFIG并网策略

2.1 DFIG的虚拟惯量控制模块

虚拟惯量控制的主要作用在系统频率变化过程的初始阶段，抑制频率的快速波动。本节中，虚拟惯量控制是在双馈风力发电机的有功功率控制系统中附加功率控制模块，将系统频率实时变化率作为控制过程的输入，通过改变转子侧变换器电流参考值改变电磁转矩，虚拟出与同步机组一样的惯性效应，响应系统频率的变化[23]。

在惯性响应过程中，DFIG的动能变为：

(12)

式中：ΔEDFIG为DFIG机组动能的变化量；JDFIG为DFIG机组的转动惯量；ωr0为DFIG转子初角速度；P、SN分别为DFIG机组极对数、额定容量。

为了更好地实现风电机组在系统频率波动时抑制波动和减小频率差的能力[24]，利用在转子动能参与电力系统调频时，将虚拟惯量控制模块引入风电机组有功功率控制系统中。

当DFIG加入虚拟惯量控制时，其动能变化为：

(13)

式中：Jequ为DFIG机组的虚拟转动惯量；ωs0、Δωs分别为系统初始同步角速度、同步角速度增量。

由式(12)和式(13)得到DFIG虚拟转动惯量：

(14)

在风电机组功率控制系统里加入附加环节，将DFIG的旋转动能转变成电磁功率后再输出，可以在一定时间内响应系统频率变化，这类比于常规发电机组的惯量变化机理。该附加环节主要是以系统频率为输入信号，建立起系统频率与风电机组有功功率之间的关系式，利用DFIG的电磁转矩来响应系统频率变化。所建立的虚拟控制模块如图2所示。图中：fs为系统频率；fn为系统额定频率，为50 Hz。

图2 虚拟惯量控制模块Fig.2 Modules of virtual inertia control

进而可以得到虚拟惯量控制模块电磁转矩增量为：

(15)

2.2 协同惯量控制策略

当风速过低时，风机转子中储存的惯量也相对较少，在风机并网时能够给系统释放的惯量相对会降低；当处于中高风速或者额定风速时，风机转子中包含一定的惯量，对维持系统的稳定性起到更显著的作用，通过对转子转速进行控制，可以给予系统更多的虚拟惯量支撑。若只采用虚拟惯量控制方式，风机转子不能给予系统足够的惯量支撑时间，且转子惯量释放完后，电网频率如果不能在短时间内进行恢复，有可能造成系统频率的再次跌落，无法短时间内对系统稳定性进行有效改善[25]。而协同惯量控制能够把转子转速控制与双馈风力发电机虚拟惯量控制有效结合起来，在控制方式上达到互补，从而达到维持系统稳定性最佳效果。

通过改变电磁转矩，能够实现DFIG虚拟惯性响应，电磁转矩的变化量决定风电机组的惯性时间常数值。本节计算双馈风力发电机并网时系统中电磁转矩增量，并建立如图3所示的协同惯量控制模块。

图3 基于协同惯量控制的DFIG模型Fig.3 DFIG model based on cooperative inertia control

图3中，虚拟惯量控制模块和转子转速控制模块相互作用于系统惯性响应的全过程，因此电磁转矩参考增量的构成如下：

(16)

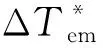
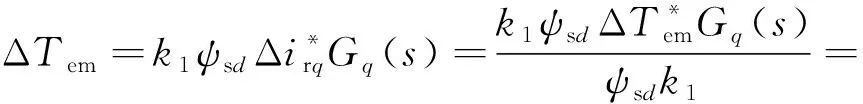
(17)

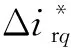
DFIG发电机转子运动方程：

(18)

(19)

式中：HDFIG为惯量响应时间常数；Tmech为机械转矩。

当转速变化时，转子运动方程为：

(20)

则增量表示的转子运动方程为：

(21)

将电磁转矩增量ΔTem代入式(21)，得到频域方程：

(22)

变换器响应时间常数很小，在此取τ=0得到：

(23)

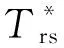
3 仿真分析

为了验证虚拟惯量控制和DFIG转子转速协同控制策略调节双馈风力发电机并网系统有功出力及频率调节的有效性，用Matlab/Simulink建立如图4所表示的风机并网系统仿真模型。分析风电并入电网下风机有功响应特性，进一步研究虚拟惯量控制和转子转速控制接入后系统的惯性响应能力，对DFIG并网系统的稳定性及惯量支撑能力展开分析。

图4 风机并网系统仿真模型Fig.4 Simulation model of wind power grid-connection system

KpT和KiT决定了DFIG受到扰动后转子转速的恢复时间。因此在图4所示的仿真系统中设置不同的控制参数KpT和KiT，结合仿真曲线对不同控制器参数在控制模块中的变化进行分析。在图5中虚拟惯量控制参数KpT值依次取-3、-2、-1观察系统稳定性。

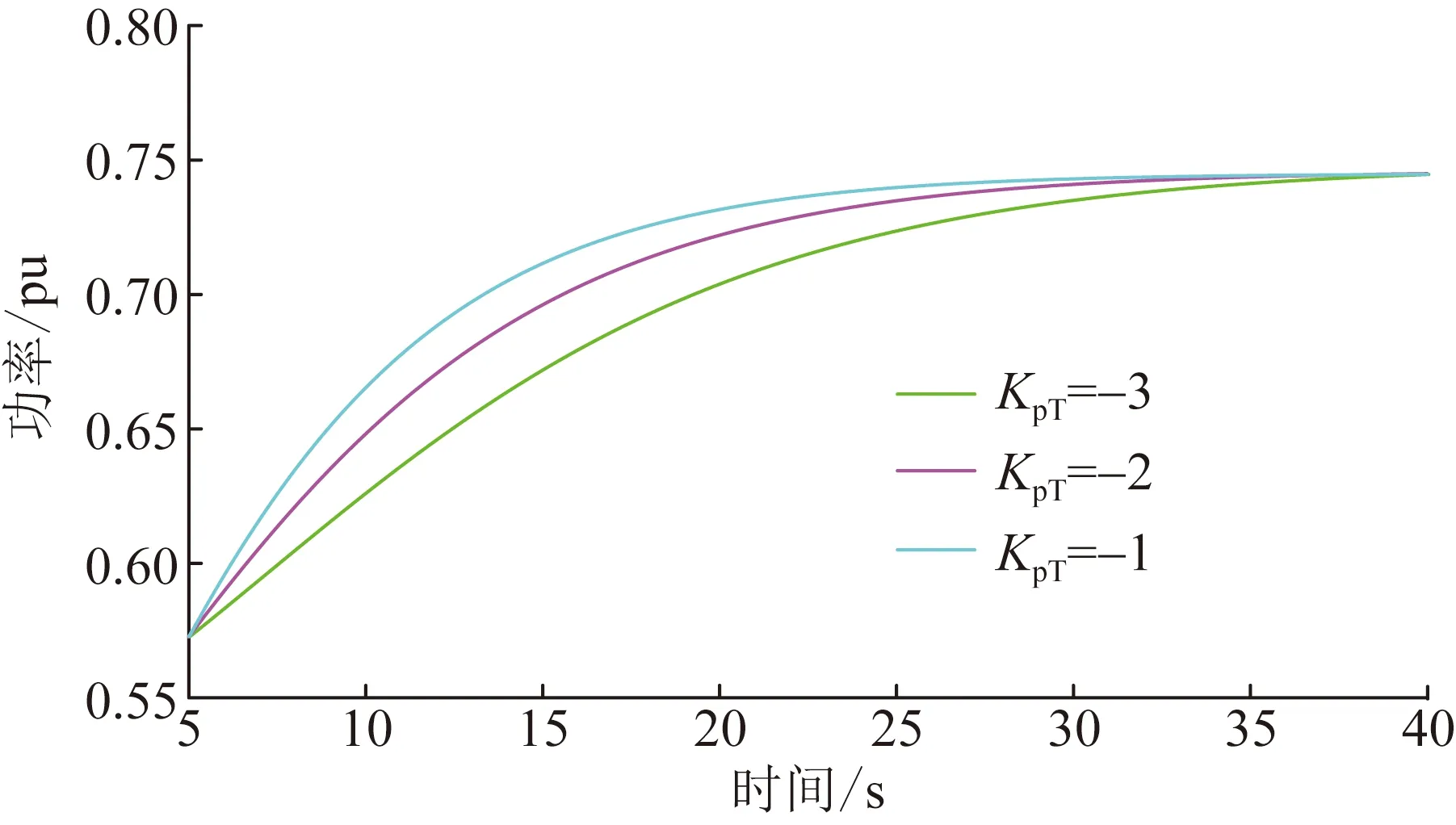
图5 KpT的变化对系统稳定性的影响Fig.5 The influence of KpT change on the stability of the system

KpT保持-2不变，组合调节转速控制模块中积分系数KiT，依次取-1、1、3，得到系统有功出力变化曲线图，如图6所示。

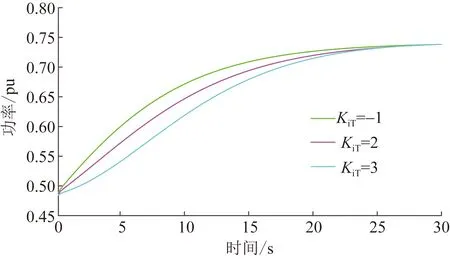
图6 KiT的变化对系统稳定性的影响Fig.6 The influence of KiT change on the stability of the system

3.1 不同工况下协同惯量控制的并网系统稳定性分析

3.1.1 风速突变时风机并网系统的有功功率出力分析

风速具有随机性且预测准确性差，风电机组的输出功率与风速的3次方成正比，小幅的风速波动也会对有功出力造成很大的影响。由于风速波动特性造成风电功率的波动，从而对系统频率产生影响。本节在风机并网系统稳定运行后的第40 s设置了如图7所示变化范围在8 ～14 m/s的阶跃风，采用协同惯量控制对该系统的输出功率和有功支撑时间进行对比分析。

图7 阶跃风速Fig.7 Step wind speed

图8给出了在风速突变情况下无附加控制与协同惯量控制下DFIG并网系统有功特性的变化曲线。由图8可知，在第40 s时无附加控制的风机并网系统的有功功率受到阶跃风速的影响，输出功率突增后有明显跌落，波动持续时间较长，恢复稳定状态速度较慢。而基于协同惯量控制下的风机并网系统受到阶跃风的影响较小，风速达到14 m/s时能够较好地适应风速突变情况。在系统输出功率发生跌落到趋于稳定的时间段内，输出功率相比于无附加控制时有较小幅度地波动，风电机组能够响应且提供了一定的功率支撑。

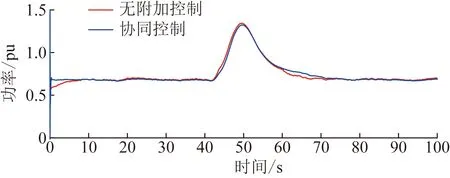
图8 阶跃风速下系统的有功出力Fig.8 Active power output of the system under step wind speed

3.1.2 短路故障下风机并网系统的有功出力特性分析

双馈风力发电机并网系统在第40 s发生单相接地故障，设置故障持续的时间为0.02 s，风电机组释放有功功率，如图9所示。从图9中可知，不含附加控制的DFIG并网系统比协同惯量控制系统释放更多的有功功率。第40.02 s故障切除后，含协同惯量控制系统释放和吸收的有功功率均比无附加控制系统少，同时含协同惯量控制的DFIG并网后系统趋于稳定的速度更快。

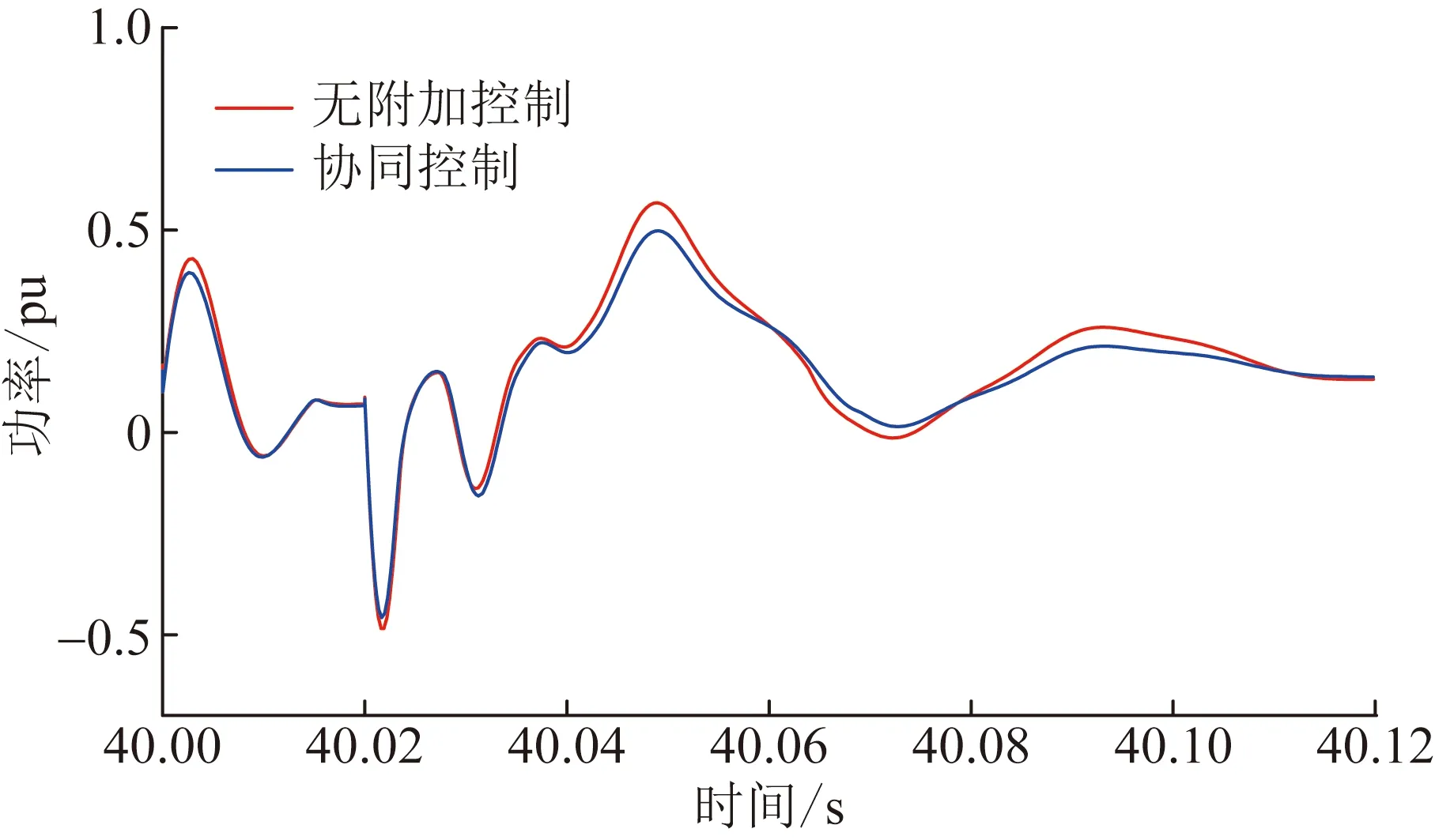
图9 单相接地时系统的有功功率Fig.9 Active power of the system when single-phase grounded

图10给出发生两相接地故障时DFIG并网系统的有功功率输出曲线。从图10中可知，DFIG在协同惯量控制的作用下减少有功出力，同时也从系统内部吸收更少的有功功率。在DFIG有功跌落时间段内，协同惯量控制对有功特性的作用并不大，二者有功出力基本一致。

在两相短路故障瞬间，协同惯量控制下的双馈风力发电机并网系统有功功率跌落较低，如图11所示。从图11中可以看到，通过DFIG快速的有功功率控制体现出更大的虚拟惯量，仿真结果证明了上述理论分析的准确性。

三相短路时系统的有功功率曲线如图12所示。图12所示工况中DFIG在有功输出恢复阶段系统仍然处在振荡过程中，这段时间内协同惯量控制动作，为系统提供了可观的功率支撑，但短暂的功率支撑引起系统较大功率波动。但是在40.05 s时，协同惯量控制使系统输出功率二次跌落的幅度减小，改善了系统暂态稳定性。

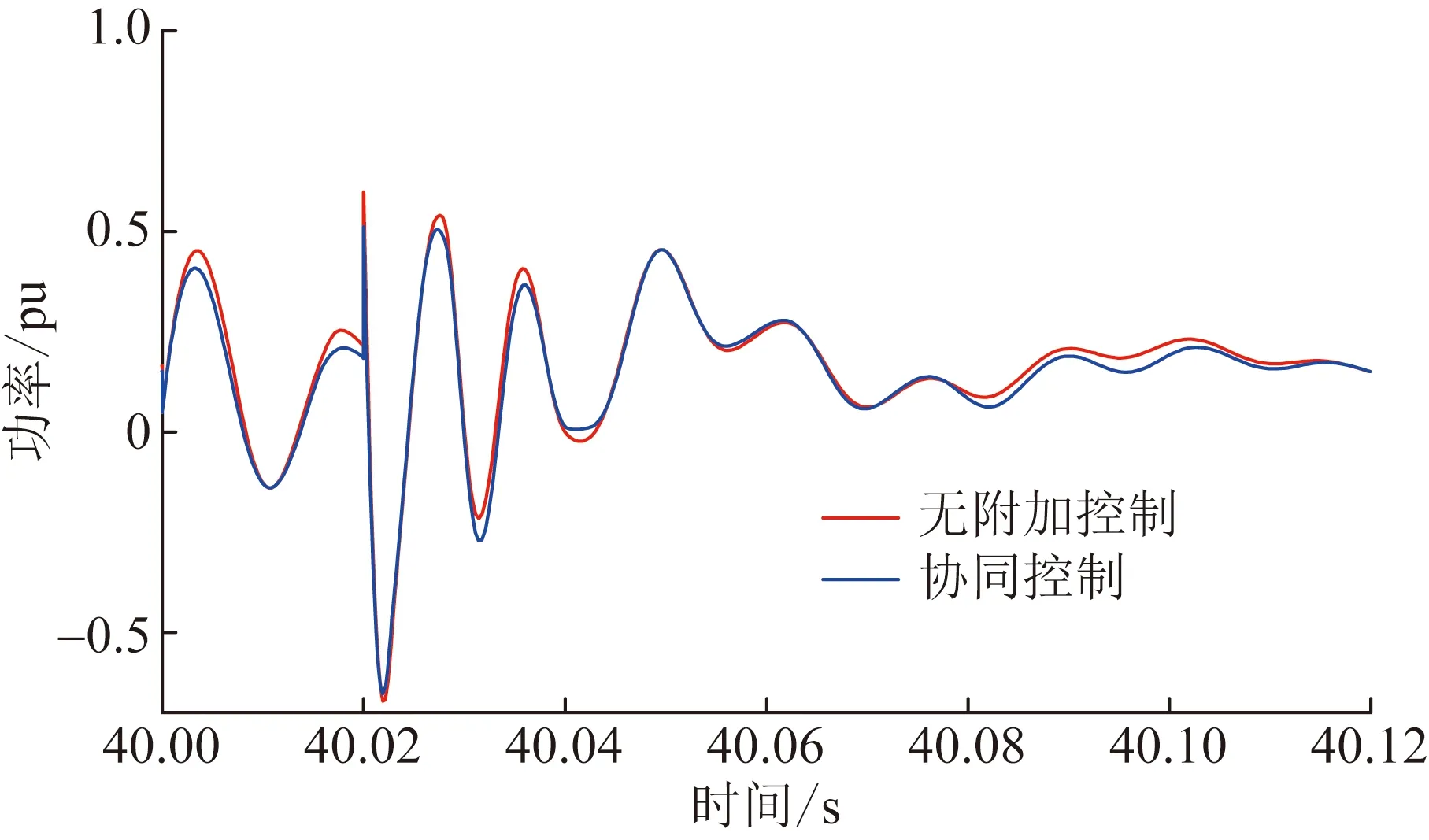
图10 两相接地时系统的有功功率Fig.10 Active power of the system when two-phase grounded

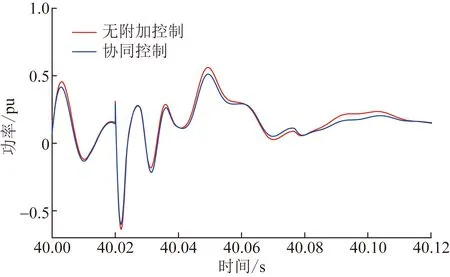
图11 两相短路时系统的有功功率Fig.11 Active power of the system when phase-to-phase short circuit

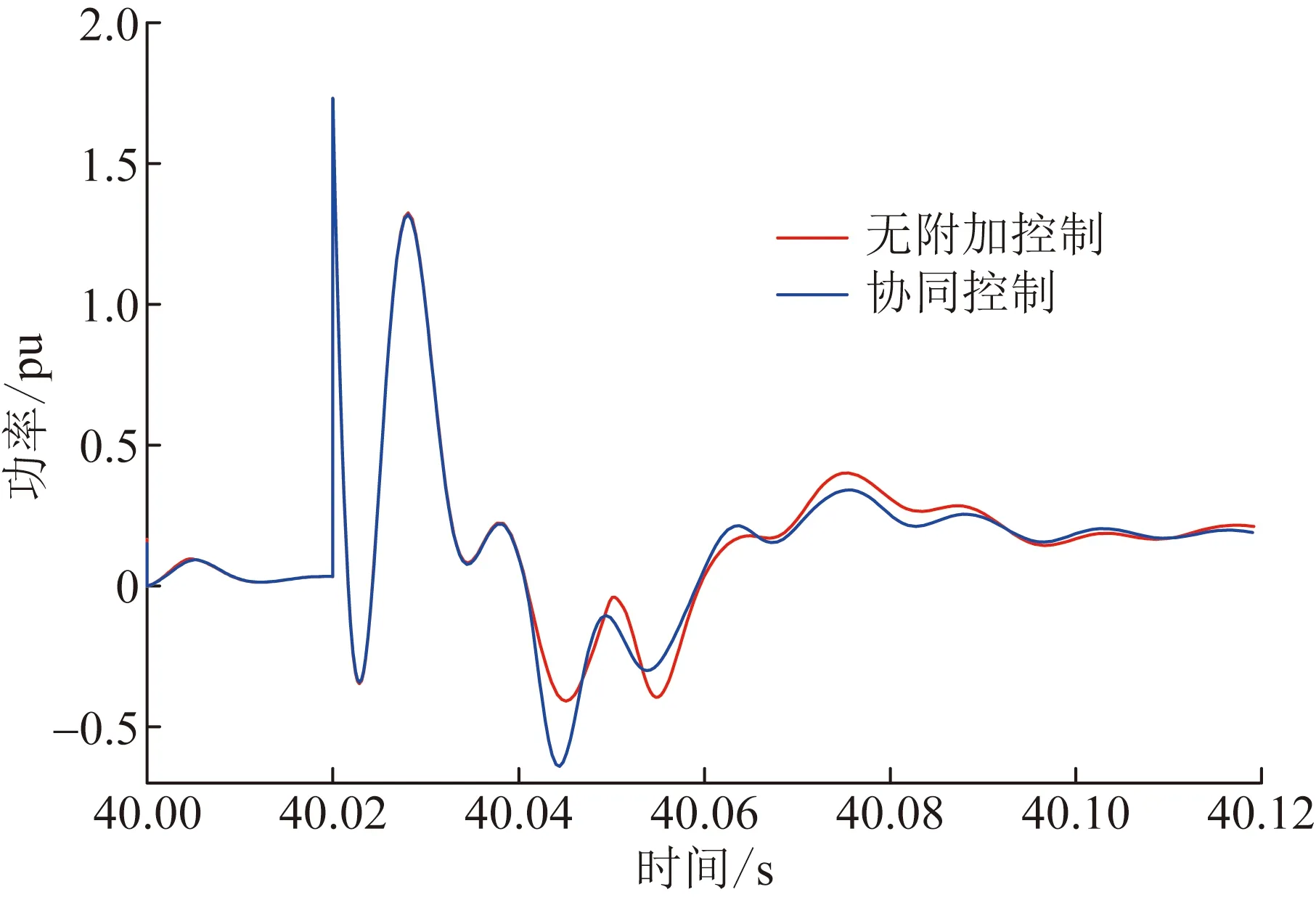
图12 三相短路时系统的有功功率Fig.12 Active power of the system when three-phase short circuit

3.2 复杂故障下DFIG并网系统稳定性分析

针对含风电的电力系统中DFIG在复杂故障下不同的出力情况，通过对控制模块参数进行调整，来满足对DFIG输出有功功率的控制，分析比较仅含虚拟惯量控制及附加DFIG转子转速控制时并网系统频率、有功出力的变化过程。

不同惯量控制下系统有功出力对比如图13所示。通过图13可以看出，在复杂故障下，DFIG未加虚拟惯量控制时，其有功出力在增加的同时引起了较大振荡。接入虚拟惯量控制后，仅能够给予系统较少的虚拟惯量支撑。

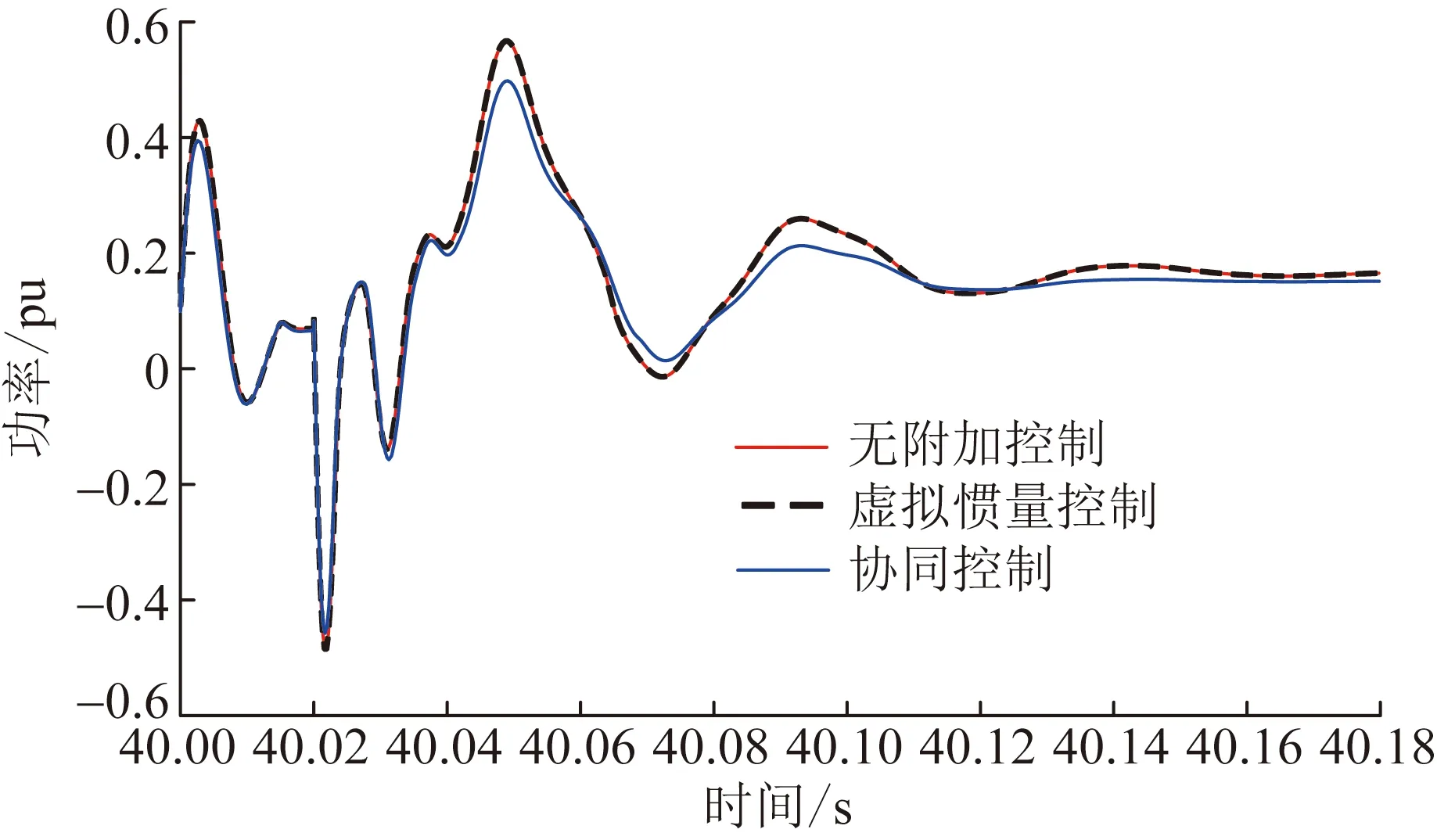
图13 不同惯量控制下系统有功出力对比Fig.13 System active power output comparison under different inertia controls

当接入转子转速控制后，两种控制模块对风电机组进行协同控制，风机启动后迅速达到稳定状态，风机的转子能够控制其自身的转速并转化转子内部隐藏的动能，向电网提供的有功功率变多。第40 ～40.02 s风机受到扰动时，功率变化得到了一定的抑制，有功出力稳定性有所提升。DFIG在动作过程中，吸收了其中部分突变功率，对风电并网系统功率恢复提供了短暂的补偿。扰动过后，风机输出功率逐渐回归稳定，为系统补偿了一定的有功缺额，可以看出DFIG并网系统有功出力相应增加。

当在风电并网系统中引入虚拟惯量控制，可使风电机组具有更大的惯性，且随着惯性响应能力的提高，含风电的电力系统频率变化幅度逐渐减弱，可以更好地维持并网系统频率稳定性。

比较双馈风力发电机并入电网后频率的变化情况，如图14所示。图14体现出伴随虚拟惯量控制的频率波动比未加入虚拟惯量控制时略微减小，而在无协同控制下，系统受到扰动时电网频率波动较大。除此之外，在协同控制策略下，系统在扰动后振荡平稳时间也相应缩短，具有较强的稳定性。

采用协同惯量控制策略后的双馈风力发电机的响应能力有所改善，风电机组通过调整系统实时频率以及频率的变化量来控制双馈风力发电机的输出功率，并在系统频率变化时利用机组的虚拟惯量为系统足够的有功功率支撑，在一定情况下能增加含风电的电力系统的频率稳定性。因此，本文所提出的协同惯量控制策略在系统不同工况下可以给电力系统提供一定时间的频率支撑，使风电机组的暂态特性更加稳定。

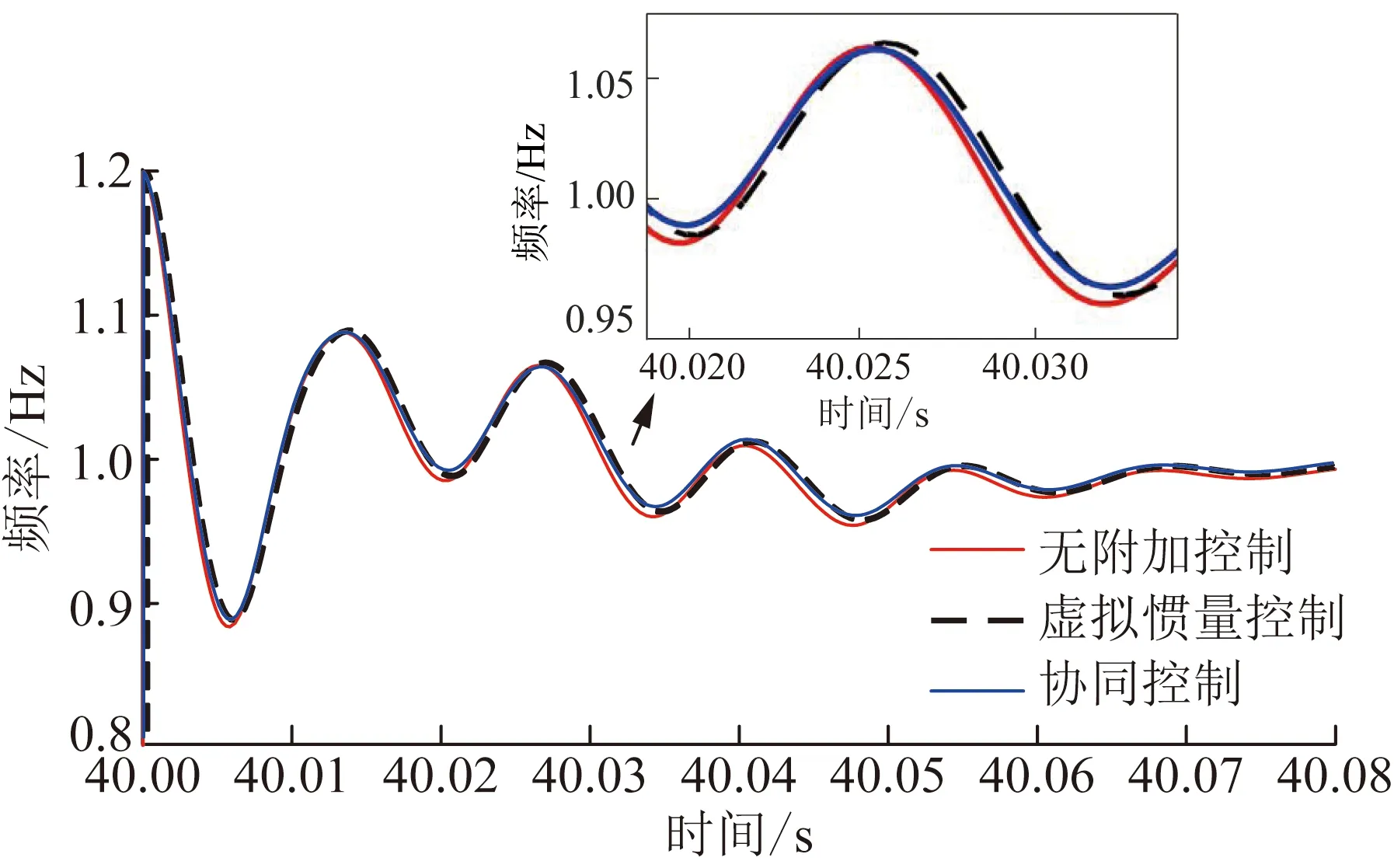
图14 不同惯量控制下系统频率变化情况Fig.14 System frequency variation under different inertia controls

4 结 论

本文针对风电并入电网后等效惯性降低，惯性响应能力减弱，对系统稳定性影响较大，提出不同于单一虚拟惯量控制的转子转速与虚拟惯量协同控制策略。经过详细理论分析和Matlab/Simulink仿真对比无附加控制、伴随虚拟惯量控制及协同惯量控制策略三种情况下双馈风力发电机并网系统的有功出力和系统频率变化过程，得出结论如下：

1)在系统处于不同工况下，DFIG利用对转子转速模块的控制，在短时间内迅速释放有功功率，增强了DFIG的频率响应性能，减小了风电并网系统中频率的波动，可以为系统带来充足的功率支撑。

2)通过仿真分析，证明了该协同惯量控制策略的可靠性，相比于无附加控制环节的含风电的电力系统，所提出的协同惯量控制策略可以改进DFIG并网系统有功功率的动态响应能力，有效提高了DFIG并网下的电力系统频率稳定性。

未来将考虑对协同惯量控制中的参数进一步优化调整，并对DFIG参与一次调频系统的稳定性展开研究。