灰色马尔科夫模型在细菌性和阿米巴性痢疾发病率预测中的应用研究

康育慧，郎丽丽，曹文君

传染病预测是传染病防控过程中的关键环节，意义在于为传染病防控部门制定应对策略提供科学依据.灰色预测和马尔科夫链预测是两种应用较为广泛的时间序列预测模型，并在传染病预测［1-3］、市场占有率［4］、商品销量预测等领域取得了较好的预测效果［5-6］.本文尝试将上述两种预测模型结合起来，应用灰色马尔科夫模型对我国法定乙类传染病细菌性和阿米巴性痢疾发病率进行拟合和预测，并与GM（1，1）模型进行比较，探讨灰色马尔科夫预测模型在细菌性和阿米巴性痢疾发病率预测中的应用价值并为制定干预措施提供参考.

1 资料与方法

1.1 资料来源

2005—2018年我国细菌性和阿米巴性痢疾发病率资料源于国家卫生和计划生育委员会出版的《2019中国卫生健康统计年鉴》［7］，2019年数据资料来源于国家卫生健康委员会网站［8］.

1.2 研究方法

灰色马尔科夫模型分灰色GM（1，1）建模和马尔科夫修正两个过程.

（1）GM（1，1）建模.①设原始非负序列为X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，对序列X(0)作1阶累加生成，得序列X(1)=(x(1)(1),x(1)(2),…，x(1)(n))，其 中，k=1,2,…,n.②对序列X(1)作紧邻均值生成，得序列Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))，其中z(1)(k)=，k=2,3,…,n.③根 据累加序列建立灰色模型的白化微分方程，其中a，b为参数，且可根据白化方程由最小二乘法估计：(a,b)T=(BTB)-1BTY，其中，…，x(0)(n))T．④求得白化方程的解为：x̂(1)(k+，k=1，2，…，n.⑤对作累减还原得灰色模型的预测值，k=1，2，…，n.⑥模型检验.对建立的灰色预测模型进行精度和拟合度的检验.利用后验差法，计算后验差比值C和小误差概率P.其中，S1、S2分别为数列x(0)(k)和残差序列ε(k)的标准差.精度检验等级如表1所示.

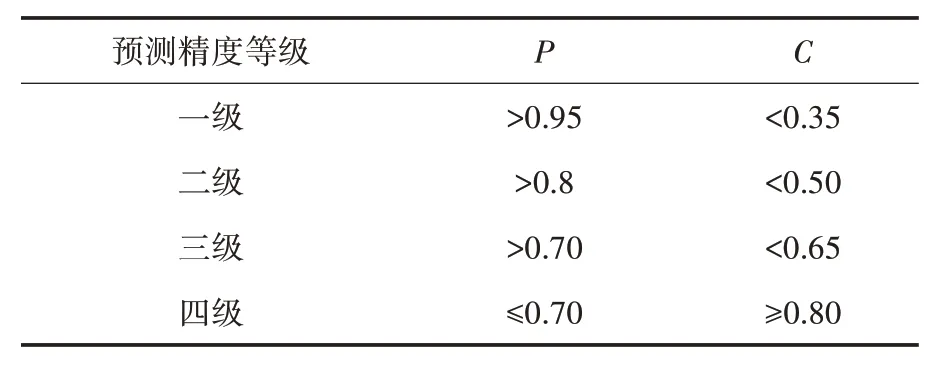
表1 精度检验等级表

（2）马尔科夫修正［9-11］.①状态划分.将GM（1，1）模型的相对误差值划分为i个状态，记为E1，E2，…，Es，列出各年份相对误差对应的状态，构建马尔科夫链.状态数与区间跨度不但与样本数量有关，而且与拟合结果的误差范围有关，一般取3~5个为佳，且保证每个区间都有数据［9］.②构造状态转移概率矩阵，其中表示系统由状态Ei经过m步转移到状态Ej的次数.③确定预测值并修正.根据建立的状态转移概率矩阵确定系统下一时刻转向状态Ei，并取状态区间Ei的中位数作为系统下一时刻预测值，则马尔科夫修正值，其中为t时刻灰色预测值，Ei-和Ei+分别为状态Ei的左右端点.

2 所得结果

全文数据处理与分析使用MATLAB R2014a软件.

2.1 模型验证

对2005—2017年全国细菌性和阿米巴性痢疾发病率数据进行拟合，对2018年和2019年的发病率数据进行预测，并与GM（1，1）模型比较以检验灰色马尔科夫模型的精度.发病率数据如表2所示.

（1）建立GM（1，1）模型.2005—2017年全国细菌性和阿米巴性痢疾发病率呈逐年降低趋势，采用MATLAB R2014a软件编程得到GM（1，1）模型的参数a，b值，a=0.124 6，b=37.811 4，由 此 得 到 预 测 模 型 为x̂(1)(k+1)=-268.587 4e-0.1246k+303.507 4，k=1，2，…，n.利用该模型得到2005—2017年发病率拟合值及2018年和2019年发病率预测值，并计算各年发病率的相对误差.结果如表2所示．

（2）马尔科夫修正.将表2中2005—2017年GM（1，1）模型相对误差值分为四个状态E1~E4，状态的区间范围分别为：（-5，-3］，（-3，0］，（0，3］，（3，6］，并得到GM（1，1）模型历年相对误差值所处状态（表2），由此建立1~4步状态转移概率矩阵，m=1，2，…，4.

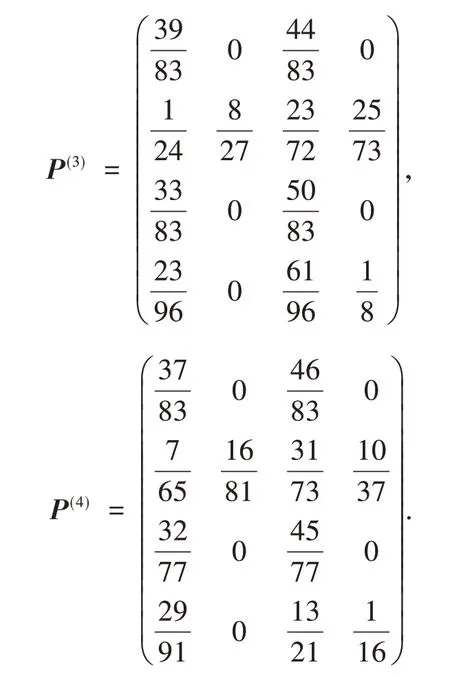
利用1~4步状态转移概率矩阵计算2018年和2019年发病率相对误差所处状态区间，2018年发病率相对误差状态预测如表3所示.

将表3中2014—2017年各状态列转移概率相加，得到2018年发病率预测相对误差转向各状态的概率分别为1.417 4、0、2.582 6、0.表明2018年发病率预测相对误差转向状态E3的概率最大，即相对误差位于区间（0，3］内，故2018年发病率预测值为7.06×≈6.95.同理，以2015—2018年数据预测2019年发病率相对误差所处状态为E3，故发病率预测值为≈6.14.结合模型中2005—2017年各年份相对误差状态可以得到表2中的灰色马尔科夫模型拟合值及相对误差情况.

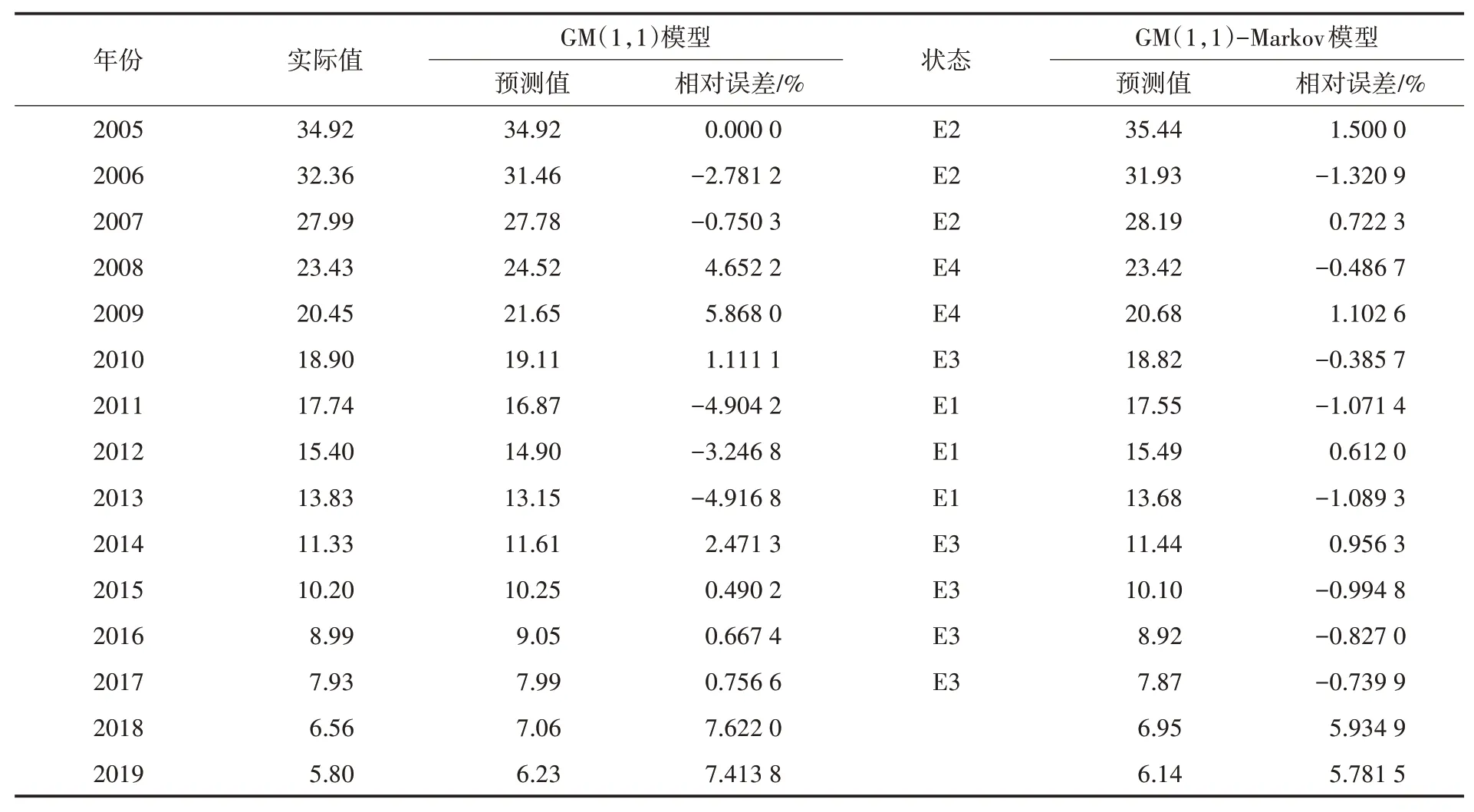
表2 各年份发病率数据及两种模型预测结果

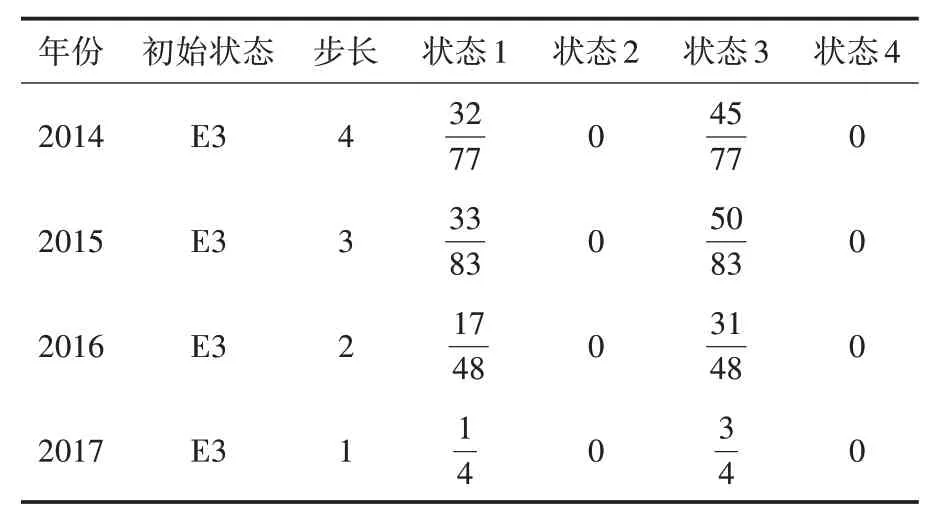
表3 2018年发病率相对误差状态预测

2.2 模型检验

根据表2数据对两种模型的精度进行比较，结果如表4所示.

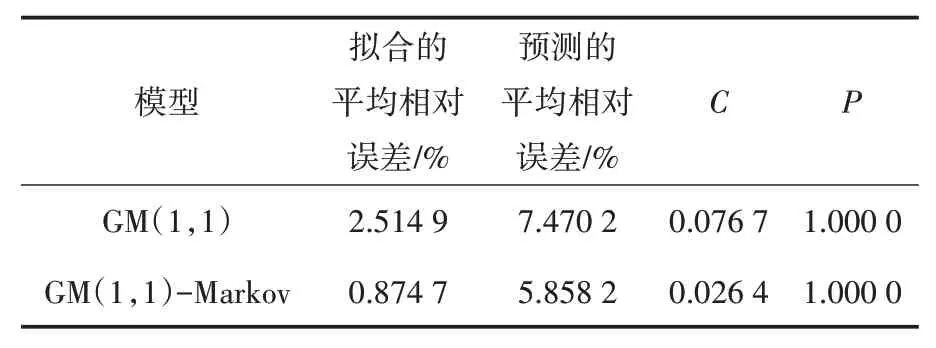
表4 两种模型精度对比

由表4可以看出，经马尔科夫修正后的灰色马尔科夫模型各项检验指标均优于GM（1，1）模型，表明灰色马尔科夫方法预测更准确，故采用GM（1，1）-Markov模型预测未来发病率.

2.3 模型预测

采用灰色马尔科夫模型，以2005—2019年细菌性和阿米巴性痢疾发病率数据预测2020年和2021年发病率.GM（1，1）预 测 模型为(k+1)=-266.626 1e-0.1260k+301.546 1，k=1，2，…，n，由此得到2005—2019年发病率相对误差并分为四个状态区间（-6，-4］，（-4，-1］，（-1，2］，（2，7］.计算1~4步状态转移概率矩阵，利用状态转移概率矩阵推算2020年发病率相对误差所处状态为E4，得2020年发病率预测值为5.17.同理，推算2021年发病率相对误差所处状态也为E4，得2021年发病率预测值为4.56.

3 结语

本研究构建了以GM（1，1）模型为基础的灰色马尔科夫模型，并运用该模型对我国2005—2019年细菌性和阿米巴性痢疾发病率进行拟合和预测以考察模型的可行性.首先由GM（1，1）模型得到2005—2019年发病率的发展趋势，进一步计算发现GM（1，1）模型拟合与预测的相对误差都较大，且相对误差序列随机波动较大，故对相对误差序列再采用马尔科夫方法修正.结果表明，经马尔科夫修正后的灰色马尔科夫模型兼顾发展趋势和随机波动两方面因素，因此其拟合值与预测值都更接近实际值，修正前后的后验差比也由0.076 7降为0.026 4，修正后模型精度相比传统GM（1，1）模型有很大提高.因此，本研究采用灰色马尔科夫模型对我国细菌性和阿米巴性痢疾发病率的预测，结果更加客观、合理、准确，可供有关部门参考.