基于双参考点前景理论求解策略的DEA交叉效率评价方法

[福州大学 福州 350108]

引言

数据包络分析（DEA）[1]是一种能够有效处理多输入多输出问题的非参数评价方法。该方法具有非参性和客观性等优势，因此受到了大量国内外学者的关注，并在诸多领域的评价问题中得到广泛应用。传统DEA方法总是从最有利于自身的角度去评价效率值，这就可能导致决策单元“孤芳自赏”的情形。针对这一缺陷，Sexton[2]等提出交叉效率评价方法，将自评思想和互评思想融合起来评价决策单元，更加全面客观地反映了决策单元的有效性，缓解了传统DEA方法的权重体系过于极端和不现实问题[3]。

随着交叉效率理论的不断发展，许多学者开始致力于交叉效率评价策略的研究。其中,大部分学者把主要研究集中在建立二次目标以进一步限制权重的模型构建上。较为经典的是Doyle和Green[4]提出的进取型和仁慈型求解策略。面对实际决策环境下仁慈型和进取型模型的选择困境，Wang和Chin[5]提出了中立型交叉效率策略，该模型只关注决策单元自身而不考虑二次目标模型对其他决策单元的影响，即不把其余DMU视为敌人或盟友。Wu等[6]通过定义某个决策单元的最优权重对其他决策单元的满意度，以最大化满意度为目标函数构建模型并提出两个算法。在现实问题中，决策单元之间可能存在着竞争或合作关系的情形，针对该问题，Liang等[7]基于博弈论提出博弈交叉效率求解方法。李琳等[8]在Liang 等[7]所提出的非合作博弈模型的基础上，根据相关权重的偏好信息进行比较，得到权重间的“相对范围”，建立基于保证域的博弈交叉效率模型，并应用于学术期刊评价研究。王旭等[9]和刘金培等[10]分别基于证据推理和群体共识提出交叉效率排序方法。李学文等[11]通过引入正则条件限制和对无效单元目标效率的限制，构建三个改进的博弈交叉效率模型，较好地解决了传统博弈交叉效率值可能不唯一和迭代速度慢的问题。

以上学者均针对传统交叉效率评价策略方法做了进一步改进，但是这些方法没有充分考虑效率评价过程中决策者的主观偏好，不能体现决策者面对收益和损失时不同的风险态度，难以很好地满足决策者的实际决策需求。针对该问题，一些学者利用前景理论引入心理因素，通过决策预期收益或损失引起的主观价值感受来反映决策者的偏好，在充分考虑决策者偏好的基础上对效率结果进行评价。例如，陈磊等[12]将决策者分为悲观、中立、乐观三种类型，计算不同决策偏好视角下的前景价值。Liu等[13]将前景理论和DEA交叉效率方法融合，评价中国23个国家重点实验室资源分配的有效性。然而，这些研究往往简单地认为决策者群体具有单一的参考点，忽视了复杂的现实中决策者参考点的多样性。实际上，受决策者性格特征、决策情境等因素影响，在决策者群体内部和外部不同评价视角下的决策者心理预期存在差异，从而导致其参考点是彼此不同的。因此，在以往的DEA与前景理论结合的研究中对决策者群体具有相同的单一参考点的假设缺乏足够的合理性。

综上所述，本文考虑决策者群体存在多重参考点的特性，结合实际决策情境，提出一种考虑双参考点的交叉效率评价策略方法，以此描述决策者多样性的心理偏好。文章首先讨论双参考点的设置，通过采用正理想解、DMU投入产出平均值来反映决策者外部竞争优势和内部自身特点。接着，针对两个参考点分别利用前景理论的价值函数计算各参照点下的价值，反映决策者对损失和收益价值感受的差异。随后，通过引入正理想点侧重系数，进一步综合各参照点下的前景价值并据此构建交叉效率二次目标模型。本文方法在完善了交叉效率DEA理论方法的同时，解决了具有多重参考点的效率评价问题，为决策者进行科学决策提供了一种新思路，具有一定的理论意义与现实应用价值。

一、理论基础

（一）交叉效率方法

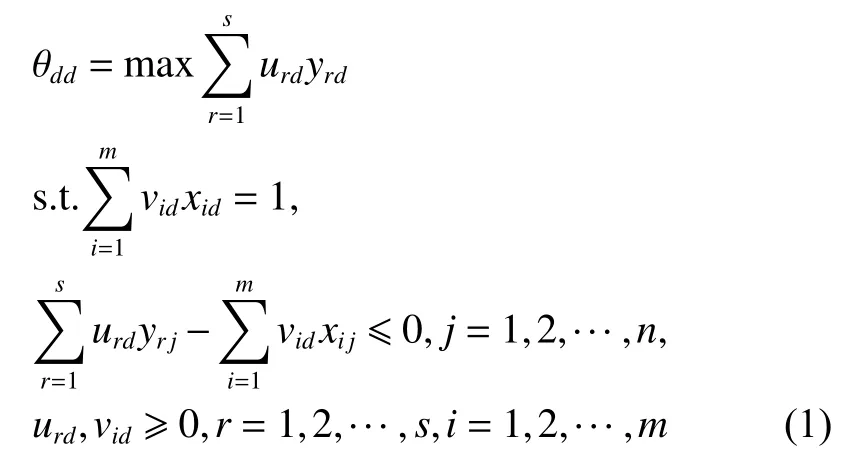
其中，θdd为DMUdd的自评效率，Urd和Vid是评价DMUdd时赋予第r种产出与第i种投入的权重。

为得出唯一的最优解，Doyle和Green[4]提出仁慈型和激进型求解策略，并在此基础上给出了两种策略所对应的、旨在得到唯一最优解的数学模型。其中，激进型模型的基本思想是最大化被评价单元效率值，同时尽可能使其他决策单元的交叉效率值最小。该模型目标函数取最小值，表明在效率评价上对所构造出来的虚拟平均决策单元是不利的，因此称为激进型模型。其数学表达如下：

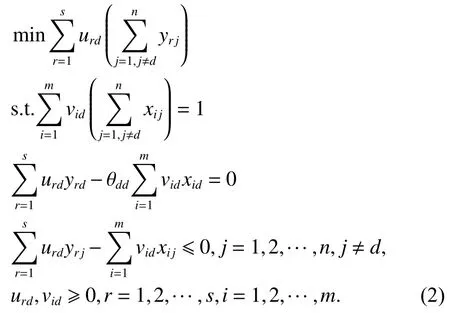
表 1 交叉效率矩阵

（二）前景理论

前景理论（Prospect Theory，PT）由Kahneman和Tversky[14]建立。该理论通过决策者面对“失”和“得”的主观价值感受差异来反映决策者的偏好，是针对风险决策的心理描述模型，被广泛应用在经济学和社会心理学等领域。前景理论中，价值函数在获得部分表现为凹函数，在损失部分表现为凸函数，且在损失部分更为陡峭，体现了个体对价值减少的心理感受更加敏感的特性。价值函数可以定义为：

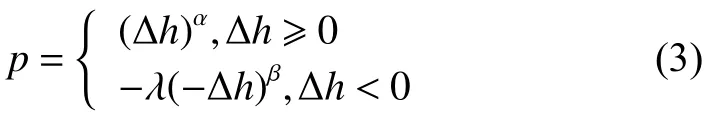
其中Δh是h与决策参考点之间的偏差，Δh=h-h0,h表示实际值，h0表示决策者参照点。参数 λ≥1α是风险规避参数，参数α、β∈(0,1]是测量远离参考点时敏感性递减的程度。Kahneman等认为，α、β参数越大则决策者对价值变化越不敏感，λ≥1表示对损失比获得更加厌恶。

二、基于双参照点前景理论的交叉效率策略模型

以往的研究大多采用单一参考点，认为决策者群体具有固定的参考点。但实际上，参考点选取受风险态度、决策者主观偏好等因素影响而具有多样性。若采用某一相同的固定点作为参考点，与实际决策者参考点存在偏差，则不能客观、可靠地反映决策者心理预期的收益和损失。参照点的设定受到任务环境、个性等因素的影响和调节,作为任务变量，参照点既可以是内源性的（决策者自发产生的）也可以是外源性的（任务的要求）[15]。因此，设置内部、外部双参考点是十分必要的，从外部竞争优势和内部自身特点两个方面来考虑决策问题，能更准确地反映决策者的心理预期，使评价和决策更加全面和科学。鉴于此，本文基于前景理论，构建考虑双参考点的交叉效率评价策略。

定义决策单元的外部参考点满足如下公式：

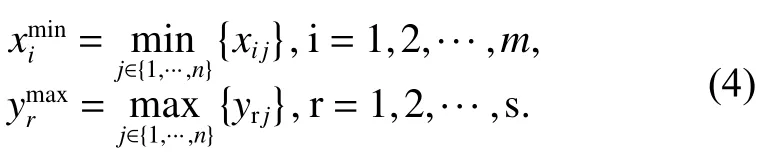
在评价过程中，同外部其他决策单元比较，可以确定该决策单元在评价系统中的竞争力，进而从外部特征上比较、分类和评估预期结果。本文选取正理想解作为外部参考点，目的是体现在整个评价系统中最具竞争力的效率值，并以此衡量不同决策者在考虑外部竞争时的心理价值感受差异。

从决策单元内部自身特点来说，在评价过程中为了解该DMU的投入产出现状水平需要设置内部参考点，考虑利用决策单元投入产出平均值作为内部参照点。平均值具有简便和代表性强的特点，以平均值作为参照点更符合决策者的思维习惯。

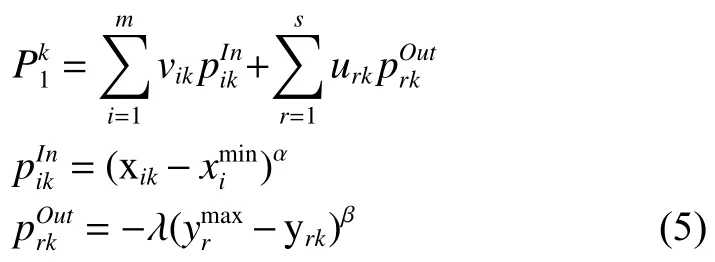
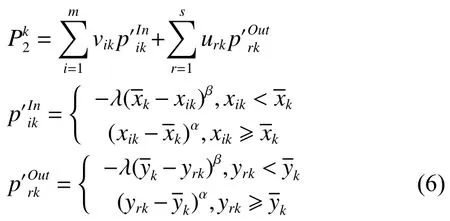
针对传统交叉效率方法中所存在的解非唯一性的问题，可以通过引入二次目标模型以进一步约束权重,在一定程度上消除解非唯一性的问题[4]。因此，本节通过建立二次规划，以最大化各决策单元的综合前景价值为目标函数，由双参照点前景理论求解策略构建交叉效率评价模型如式（7）：

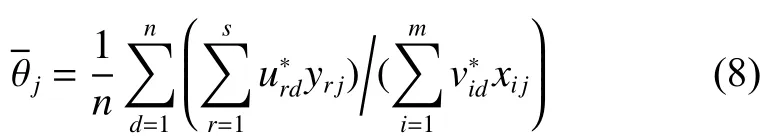
综上所述，基于前景理论考虑双参照点的交叉效率评价策略步骤如下：

步骤1设置双参考点。考虑从DMU外部竞争优势和内部自身特点设置双参照点，采用正理想解、DMU投入产出平均值分别作为外部、内部参考点。

步骤2针对两个参考点分别利用前景理论的价值函数计算各参照点下的价值。基于前景理论，利用式（5）和式（6）分别表示针对双参照点的价值。

步骤3综合两个参照点下的前景价值，构建反映决策者偏好的交叉效率二次目标模型。通过引入正理想点侧重系数，进一步整合各参照点下的前景价值，利用式（7）构建考虑双参考点的交叉效率策略模型，求解并得到改进的交叉效率矩阵。

步骤4对改进的交叉效率矩阵进行集结并排序。由式（7）所得的是交叉评价策略输入输出的权重、，利用这些权重确定交叉效率矩阵，并采用相加平均的集结方法对交叉效率矩阵进行集结，最终得到各DMU交叉效率值。

三、案例分析

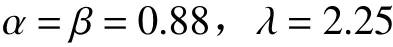
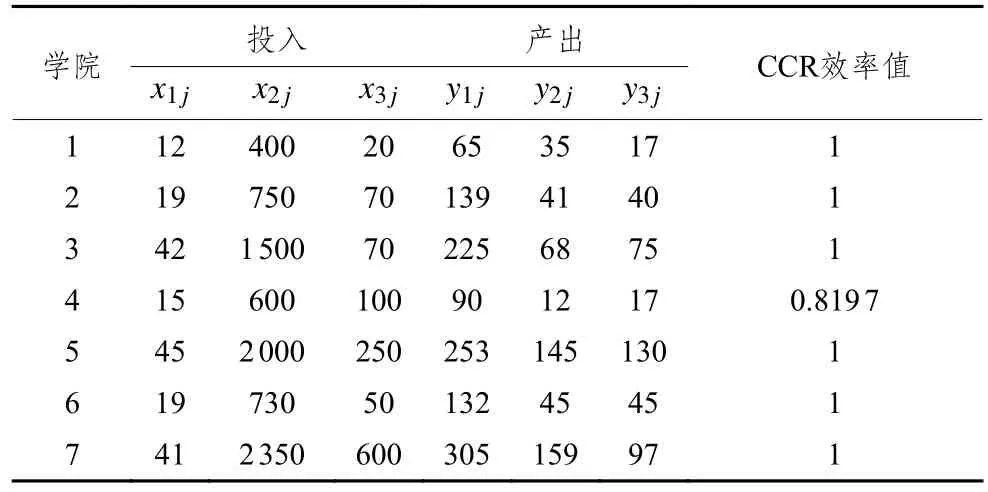
表 2 7个学院投入产出数据

由表2最后一列可知，存在多个自评效率为1的决策单元，且无法进一步区分这些决策单元的效率大小，这说明传统CCR模型难以实现全排序，且容易导致效率评价结果虚高。因此，引进交叉效率评价方法是很有必要的。通过激进型交叉效率模型对该算例进行评价，其所得交叉效率矩阵如表3。结果表明，交叉效率方法能够实现全排序，且自评和他评相结合的评价视角更为全面科学。但是，传统的激进型和仁慈型模型将其余DMU全部视作敌人或盟友，这与现实世界的决策情景有所不符,而且会因评价结果不一致而导致实际应用中难以对它们予以抉择的难题[17]。

利用本文所提出的考虑双参考点前景理论的交叉效率评价策略，根据式（5）～（8）计算各决策单元交叉效率值，具体结果如表4所示。

表 3 激进型交叉效率矩阵

表 4 改进的交叉效率矩阵

对比表4和表3的排序结果可以看出，一些决策单元的排序发生了较大幅度的变化。如第4个DMU排序结果从第7位跃升到了第3位，这是因为本文方法结合前景理论的概念，充分考虑决策者主观偏好,认为不同决策者对收益和损失的感知价值存在偏差，从而导致最优权重有所不同。为了进一步说明本文方法的有效性，本节选取经典的交叉效率模型方法来对该案例的交叉效率值进行求解，并将其效率值与本文提出的模型结果相比较，具体如图1所示。

图 1 不同方法下决策单元交叉效率值比较

表4和图1的计算结果表明，7个DMU中有6个DMU的排序结果都发生了不同程度的变化，其中，DMU1的改进效率值为0.753 6，排序结果下降到第4位，DMU2的改进效率值为0.886 7，排序结果上升至第2位，这是因为本文在结合前景理论的基础上，考虑决策者参考点的多样性，在不同视角的参考点设定下，决策者的参考点取值各不相同所导致的。可以看出，改进后的策略模型能更准确地描述在复杂实际问题中决策者心理的多重参考点，据此构建的二次目标交叉效率的评价策略模型更具有合理性。

值得一提的是，在图1不同方法比较的结果中，以DMU4为例，其CCR效率值为0.819 7，进取型效率为0.401 8，仁慈型效率为0.616 0，排序均为最后一名。而采用本文方法计算效率为0.851 1，排名攀升至第3名。除了原始数据本身所造成的影响之外，排序变化的根本原因是二次目标策略构建思路的不同，改进方法的评价维度更加全面使得评价结果出现差异。本文方法对不同类型的决策者采取了不同的比较标杆，进而影响决策评价过程中最优权重组合的选择。因此，DMU4排名的骤变恰恰体现了决策者心理预期差异对评价结果产生的影响。

综上所述，本文所提出的考虑双参考点前景理论的效率评价方法能够通过设计内、外两个参考点从外部竞争优势和内部自身特点来反映不同类型决策者迥异的心理预期，体现其面对收益和损失时风险态度的差异性。这使得决策者对评价结果的满意度更高，得到全面合理的效率结果，也更有利于决策者做出科学的决策判断。

四、结束语

现存的有关DEA交叉效率评估方法的文献中，较少关注决策者的主观偏好对交叉评价策略构建的影响。为此，本文借用前景理论，以不同决策者所表现出的参考点多样性问题为突破口，从参考点所满足的内、外部特征入手，建立能反映不同决策者心理预期值的二次目标交叉策略模型，更准确地计算前景价值并据此求解交叉效率结果。算例表明，本文方法能得到稳定、合理的评价排序结果。综上所述，本文方法是将前景理论的研究结果应用于DEA数据包络分析的一种创新，也是对现有交叉效率评价策略的补充，对于探索现实中决策者的科学决策具有重要意义。