运载火箭滑行段姿控喷管故障自主辨识方法

纪 刚 陈 平 张惠平 胡煜荣 禹春梅

北京航天自动控制研究所， 北京 100854

0 引 言

近几十年，航天器故障诊断取得快速发展，故障预测与健康管理(Prognostic and health management，PHM)和飞行器综合健康管理(Integrated vehicle health management，IVHM)等相关技术概念在很多文献中被提及，核心都是故障诊断与容错控制技术[1]。现有的故障诊断技术可大致分为基于模型的方法、基于数据的方法和基于知识的方法3类[1,2]，基于模型的方法通常通过解析冗余来诊断故障并进行故障的处理[3,4]。吴德安提出了系统发生故障时，故障部件的自主隔离、备份部件自主切换和系统重构方案[5]，王大轶系统性地阐述了航天器故障诊断和重构技木[6]，樊雯等对姿控系统的可重构性进行了分析探索[7]，胡宇桑等对可重构性综合评价方法进行了研究，为控制系统可重构性综合设计提供了优化决策方案[8]，也为卫星混合执行机构可重构性评价和设计提供了相关参考[9]。航天器故障诊断和控制重构在理论方面取得了很多成果，同时在“资源一号”卫星、“风云卫星”等航天器上进行了实践，轨道运行的航天器故障诊断已经从理论研究向工程实践迈出了很大的一步。航天器轨道飞行场景下本体动态条件变化相比不大，通过这些方法在线实现故障诊断有较好的基础，同时也可以利用天地信息交互实现离线的故障诊断等工作。

液体运载火箭真空滑行段采用姿控喷管进行姿态控制，但因飞行时间短，实时性强，运载能力限制等因素，很少在线进行故障诊断。国内外宇航领域多次出现姿控喷管故障导致飞行失利的情况，因此需要快速地对故障进行定性，确定故障程度，为故障的处理提供依据。液体运载火箭姿控喷管故障诊断的国内文献较少，张亚婷等提出姿控喷管的故障诊断方法，即通过设计观测器，对比观测器输出信号和真实信号的残差判定故障是否发生[10]。张凯等提出的基于跟踪微分器的姿控喷管故障检测较好地解决了刚体模型下的故障辨识问题，但没有对故障类型和程度给与评价[11]。陶文华等提出了利用关系矩阵在航空发动机故障诊断中的应用[12]。

针对运载火箭滑行段姿控喷管故障诊断的问题，本文对箭体动力学模型进行推导得出姿控喷管指令、晃动与箭体角加速度的关系式，利用关系矩阵证明了故障辨识的条件，建立了典型姿控喷管故障诊断的逻辑方法，典型仿真证明了方法的有效性。

1 液体运载火箭滑行段数学模型

1.1 滑行段绕心运动模型

运载火箭滑行段飞行，姿控喷管的燃料消耗量有限，箭体参数几乎不变。滑行段主发动机贮箱的燃料晃动必须考虑，一般绕心动力学模型表示如下：

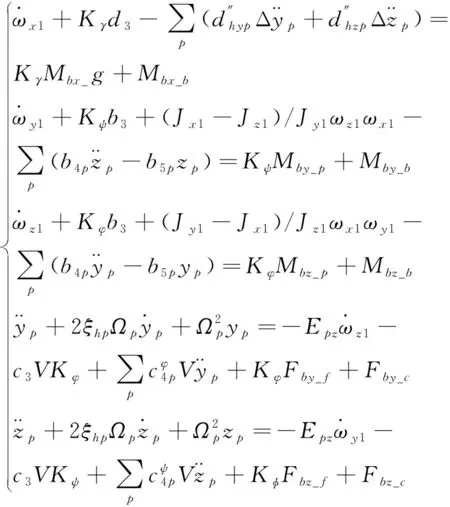
(1)

其中,Kφ,Kψ,Kγ分别为俯仰、偏航和滚动通道的控制指令，ωz1，ωy1，ωx1分别为绕箭体坐标系o1z1，o1y1，o1x1的角速度，yp，zp分别为法向和横向晃动位移。

式(1)需要图1中的姿控喷管喷流产生的控制力矩来实现火箭的稳定飞行。运载火箭一般不对姿控喷管进行实时监测，基于式(1)描述的模型，采用裕度设计的思想取得一定的容错能力。运载火箭滑行段飞行与在轨运行的航天器都会采用姿控喷管进行姿态控制，但差异突出，集中表现在火箭飞行时间短，突发故障需要及时处理；受运载能力限制，不在线对姿控喷管进行监测；火箭主发动机贮箱液体晃动引起的力和力矩必须考虑。

图1 姿控喷管典型配置方式

晃动，一般是指贮箱中液体自由表面的周期性运动[13]。姿控喷管在响应控制指令的同时，会对晃动运动产生激励。以俯仰通道为例，从运动方程(1)上可以看出，在姿控喷管开启的过程中，箭体的角加速度可以表示为

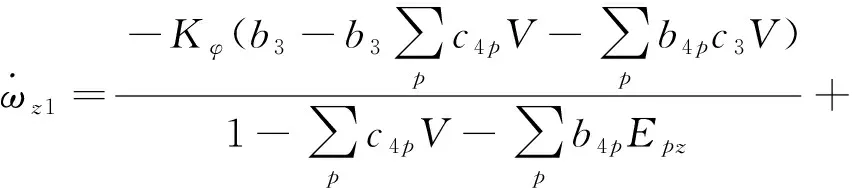
(2)

式(2)表示箭体俯仰角加速度与姿控喷管指令、控制力矩、弹道参数有关，从图2可以看出姿控喷管激励出的俯仰通道箭体角加速度比b3大了约50%，通过姿控喷管控制指令可以建立起与俯仰通道箭体角加速度的关系。偏航通道类似，滚动通道一般可以不考液体虑晃动因素。

图2 模型角加速度与控制力矩系数b3的对比

1.2 基于执行效果的姿控喷管故障模型

运载火箭典型姿控喷管系统一般为单组元恒压挤压推进系统，单组元发动机工作时，推进剂由喷注器进入催化床，经催化分解为高温燃气，高温的混合气体经喷管膨胀产生推力[14]。陈新华，朱定一从姿控喷管的系统构成上，根据设置的故障树，利用可靠性指标以及实际飞行中收集到的故障现象，建立了故障推理知识库，实现对故障的辨识[15]。但姿控喷管中任何对推力产生过程有影响的部件都是潜在的故障发生点，并最终决定姿态控制的品质。

从式(1)可以看出，姿控喷管作为姿态控制系统的执行机构，依据动力学模型的实际表现，按类型可将故障分为3类：1)常开故障。动力学表现为姿控喷管在关机指令发出后依然为常值推力输出；2)常闭故障。动力学表现为姿控喷管在开机指令发出后依然为零推力输出；3)极性故障。系统形成了正反馈。而介于这些故障定义之间的模式，例如推力下降等，均可以结合实际需要进行定义。从动力学模型的角度对这些典型故障类型进行研究，可暂不考虑姿控喷管推力偏差等问题。从图3控制指令与推力的关系上进行比较说明，当控制指令Ki(i=φ,ψ,γ)发出后，对应推力上升到额定推力P0附近一定偏差范围内，可认为无故障；如果推力未达到，处于很小的推力PB附近，则可认为发生了常闭故障；当推力符号反向处于PJX附近则可认为系统极性错误。当控制指令Ki关闭，推力未明显下降，则可认为发生了常开故障。

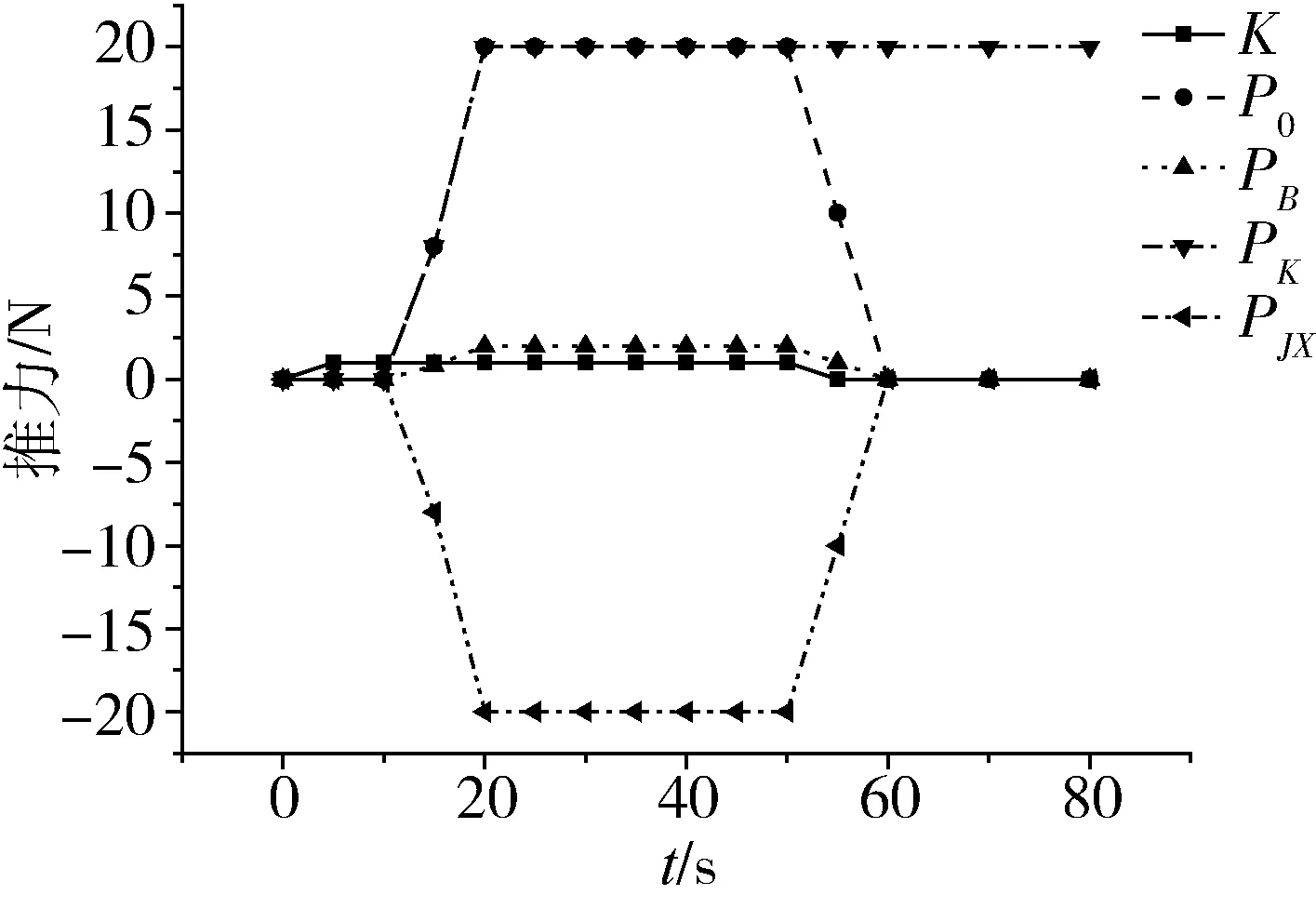
图3 典型故障类型下控制指令与推力

图3中Ki为控制指令，P0为未发生故障的推力，PB为常闭故障的推力，PK为常开故障的推力，PJX为发生极性故障的情况。

2 姿控喷管故障辨识

2.1 基于关系矩阵的姿控喷管故障可辨识性

液体运载火箭是一个非线性较强的飞行器，刚体、晃动模态是飞行过程中姿控系统需要考虑的关键因素，为了方便研究火箭滑行段姿控喷管故障诊断问题，采用式(1)的小偏差模型进行研究。

首先，考虑一个n阶，r维输入，q维输出模型描述如下。

(3)

其中,u(k)为火箭姿控系统控制输入，y(k)为姿控系统获取的测量信息。经过p(p>0)步后，箭体控制输入和绕心测量信息表示为

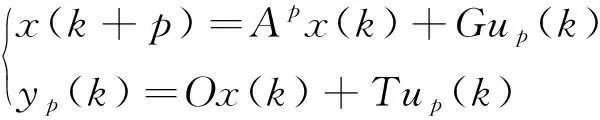
(4)

引入关系矩阵引入相互关系影响矩阵Mi，可以推导出k+p时刻系统输出如式(5)所示二者关系，

(5)

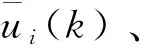
2.2 故障诊断方法

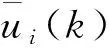
当姿控喷管发生故障时，姿态控制系统测量信息和理论信息会产生很大不同，偏差估计是故障决策的重要部分。姿控喷管故障时，系统偏差会与理论值发生较大差异，为描述方便认为偏差的变化仅与故障发生的有关系。

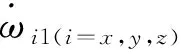
(6)

建立模糊映射关系，假设故障类型的集合为Y={yi|i=1,2,…,n}，式中n为故障类型总数，本文仅对动力学描述上的故障进行分析，因此此处的n=3，分别表示常开、常闭和极性三类典型故障。由这三类典型故障类型引起的故障征兆定位另一个集合X={xj|j=1,2,…,m}，式中m为故障征兆的总数，对于单个通道而言，至少包含角偏差、角速度以及角加速度，根据前文分析，此处的m=1。

根据模糊集合理论，故障类型的模糊集合与它们的各种故障征兆的模糊集合之间存在一定的逻辑关系:

Y=X°R

(7)

式中：°为模糊算子，R=(rij)n×m为模糊关系矩阵。结合火箭动力学模型，式(7)的表达式可以转化为Y=(Ki∧X)°R，其中Ki为前文所述的控制指令状态，即该模糊关系的表达与控制指令状态存在“与”的关系。模糊关系矩阵表达如下

(8)

式(8)矩阵R表示故障类型和故障征兆之间的因果关系，矩阵元素rij代表第i个故障征兆xj对第j个故障类型yj的隶属度，有0≤rij≤1(i=1,2,…,m;j=1,2,…,n)。第j个故障类型引起第i个故障征兆的可能性越大，隶属度的值越大。隶属度取值的原则，以俯仰通道为例，箭体姿态角和箭体角速度的变化耦合原因因素太多，对应三类故障类型rij的取值较小。式(2)所示的角加速度变化，与故障类型有着紧密的隶属关系，如果与控制指令结合，rij的取值接近于1。为了工程应用方便，式(8)可简化为R=[r11r12r13]，即行数为1，列数为3的矩阵，矩阵元素数值均为1。故障诊断的方法实际上可以简化为控制指令、姿控喷管故障类型、角加速度偏差量三者之间的对应关系，图4给出利用角加速度偏差进行故障诊断的原理图。

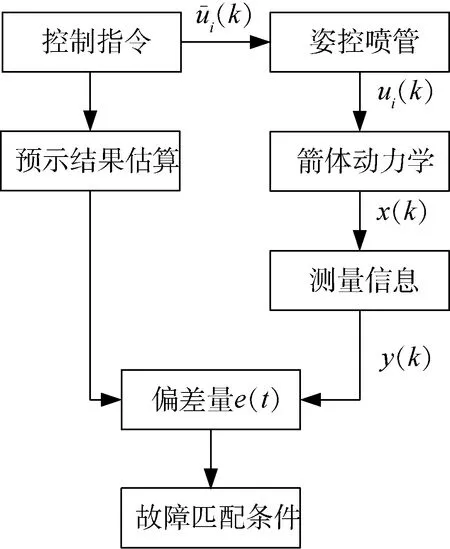
图4 典型故障诊断计算流程

利用发出“开”控制指令后的动力学表现进行姿控喷管常闭故障与极性故障的判别，利用“关”控制指令后的动力学表现进行姿控喷管常开故障的判别。选择式(6)公式求取偏差e(t)，当实际测量滤波输出值与理论模型预示值满足条件

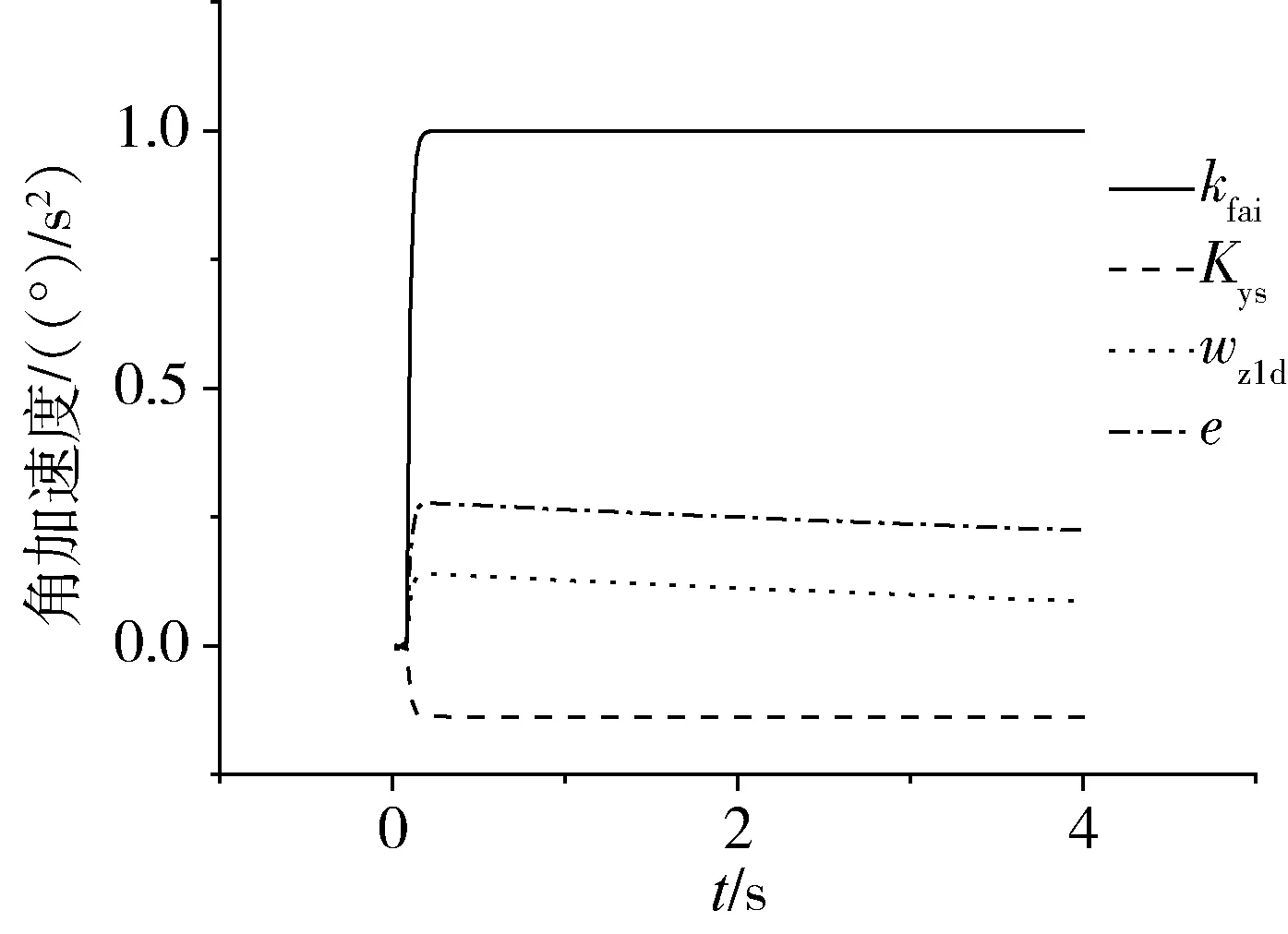
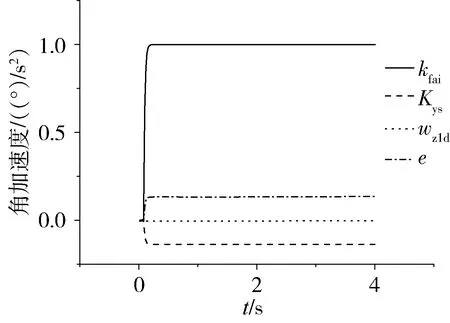
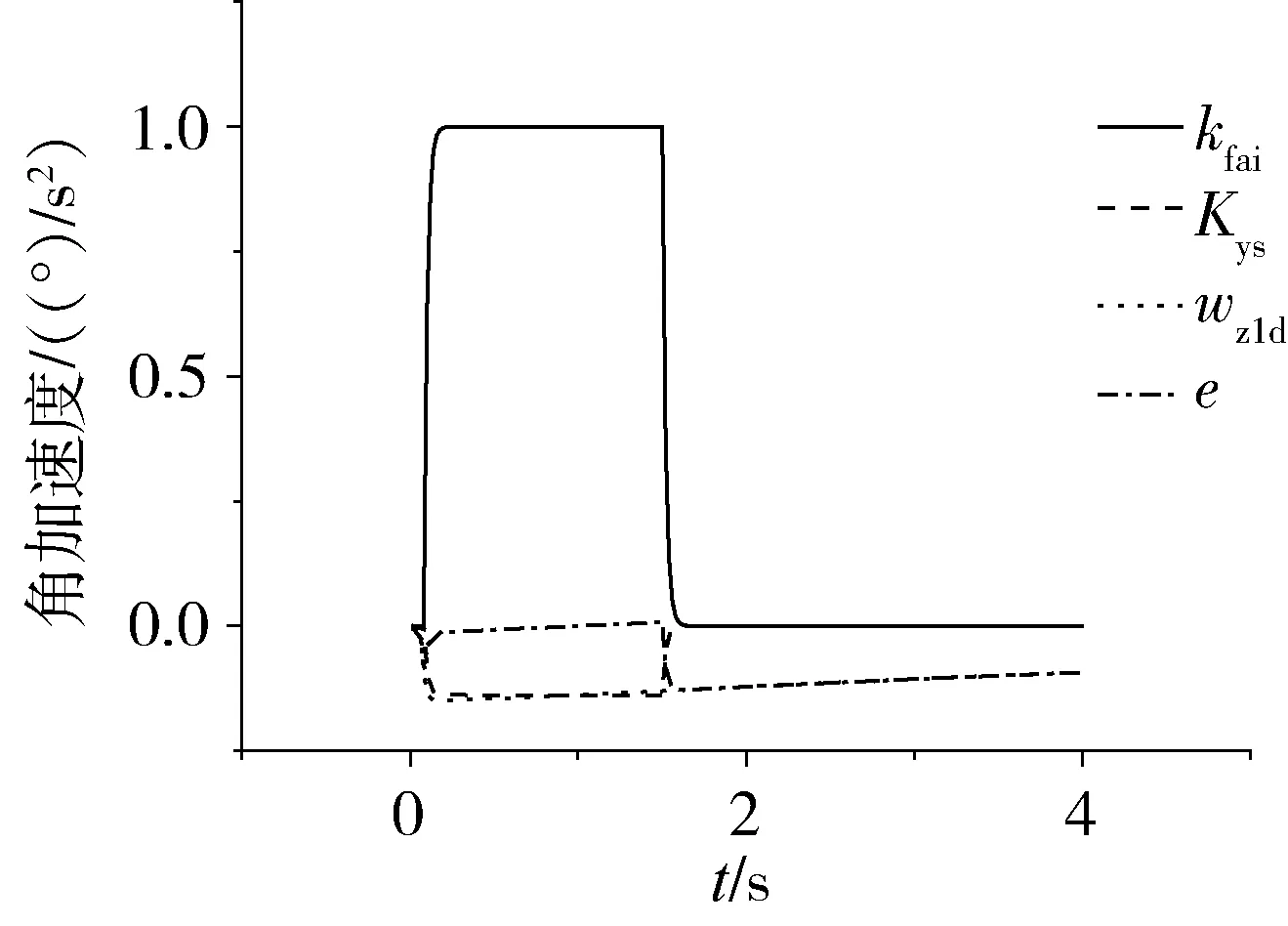
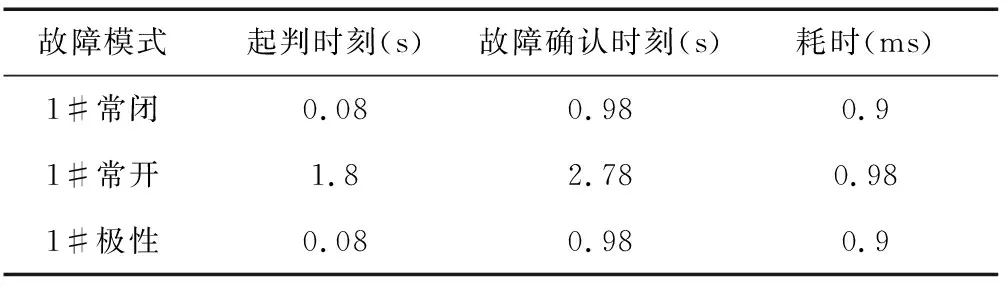
K(nT)≠0^K((n-1)T)=0^(-η

则认为姿控喷管工作正常；当满足条件K(nT)≠0^K((n-1)T)=0^{e(t)≅-φ(Kc(t)≠0)±η}则认为出现常闭故障；当满足条件

K(nT)≠0^K((n-1)T)=0^{e(t)≅φ(Kc(t)≠0)±η}则认为存在极性故障；当满足条件

K(nT)=0^K((n-1)T)≠0^{|e(t)|≅φ(Kc(t)≠0)±η}则认为存在常开故障。其中的η是考虑箭体模型参数偏差、喷管推力偏差等之后的条件误差。

2.3 故障诊断门限确定

基于箭体动力学特征进行典型故障的诊断，逻辑需要合理，故障诊断的门限也尤为关键。故障诊断门限选取原则是不误判，不漏判，误判可恢复且不带来次生灾害。故障诊断门限选择涉及多个因素，首先是姿控喷管推力特性。计算机发出控制指令Ki之后，经过驱动电路操作姿控喷管电磁阀开合，燃料在燃烧室燃烧后产生推力。门限参数的选择需要考虑推力上升和下降的过程，t90、t10参数与控制指令Ki生成存在时间差。其次，惯性测量装置本身的量化误差也决定了故障诊断门限的大小，尤其是最小值。假设角运动测量当量为1.0角秒/脉冲，惯性测量装置能够敏感的每20ms控制周期内的角增量最小为0.000278°，折合角速度约为0.01389(°)/s，角加速度约为0.6944(°)/s2。采用角偏差、角速度或是角加速度，均需要结合量化误差综合考虑。另外还有箭体飞行振动环境下，箭体各种扰动频率分布，采用均值计算等方法，可以提升门限适应能力。

3 仿真分析

以某运载火箭滑行段俯仰通道为例进行仿真，假定进入滑行段后，初始姿态角偏差为2.0°，角速度0.5(°)/s，分别设置常闭、常开和极性故障进行仿真。常闭故障和常开故障可以在飞行中的某个时刻选择注入，此类故障发生时机根据实际的案例看是可以随机的，为方便说明，均在第一次需用时刻设置故障。

图5～ 8中给出了姿控喷管各种典型工作情况下的仿真结果，其中kfai表示控制指令，Kys表示箭体角加速度预示结果，wz1d表示喷管产生的箭体角加速度，e为角加速度的误差。正常工作条件下，角加速度的预示值和实际箭体产生的角加速度，与控制指令有很强的对应关系，e也处于合理的偏差范围之内。常闭、常开以及极性故障状态下，控制指令kfai，箭体角加速度预示值Kys、箭体实际角加速度wz1d的映射关系处于异常状态，e的特征显著。通过故障诊断条件选取合适门限，可以对这3类典型故障类型进行有效辨识。

图5 正常状态角加速度仿真曲线

图6 常闭故障模式仿真曲线

图7 常开故障模式仿真曲线

图8 极性故障模式仿真曲线

运载火箭飞行动态强烈，因此故障发生之后，辨识的最佳时机是故障发生的初始时段，随着故障对箭体运动的持续激励，特征参数会随着通道之间运动耦合产生交联效应，这会使故障诊断难度增加。表1给出了3类典型故障诊断确认的时间，从辨识的结果可以看出，采用本文所述的辨识方法可以快速给出故障结论。

表1 俯仰通道姿控喷管故障仿真结果

4 结 论

液体运载火箭姿控喷管在线实时故障诊断，需要考虑大贮箱液体晃动对箭体运动学参数的影响，飞行环境与轨道运行的航天器也有很大的区别。采用本文所述方法进行辨识，可以准确诊断出姿控喷管发生故障的动力学模式，但同时也需要看到，本文所述辨识的方法是基于火箭动力学模型的，各种故障模式假设下的诊断结果，与姿控喷管系统实际真实故障存在定义上的差异，要实现准确的故障定位，还需要结合姿控喷管动力系统信息进行故障信息融合辨识。