视线制导坐标系下空间自主交会故障诊断与容错控制集成设计

刘伟杰 陈 斌 冯佳佳

1. 北京控制工程研究所，北京100094 2. 空间智能控制技术重点实验室，北京100094

0 引言

20世纪末以来，空间自主交会对接技术得到了越来越多的应用。在自主交会最终逼近段的接近轨迹设计及其相对应的故障诊断、隔离与恢复，被认为是自主交会最主要的技术难点[1]。在这一阶段，追踪航天器可能受到帆板的挠性运动、液体晃动等干扰，另外还因为轨道摄动、各种导航和控制误差、推力器故障等原因，导致实际轨迹与计划轨迹之间会产生偏差[2]，这也增加了追踪航天器故障诊断的难度。目前对于推力器故障的容错设计主要是针对被动轨迹保护和主动轨迹保护两大类方法[2-3]。采用解析模型故障诊断与容错控制的思想研究这一问题的文献还比较少见[4-5]。针对航天器圆轨道自主交会问题，刘伟杰在考虑推力器输出约束的情况下，完成了故障诊断与容错控制的集成设计[6]。需要注意的是，航天器自主交会过程中追踪航天器一旦发生故障，就需要航天器在极短的时间内完成故障的诊断与隔离，否则航天器会偏离规划轨迹，而这往往意味着交会任务的中止。

近年来，故障诊断与容错控制集成技术由于其高可靠性及兼顾诊断性得到了越来越多的关注。Nett首先提出了故障诊断与容错控制集成设计思想[7]，并设计了一个四参数集成控制器。陈雪芹针对航天器执行机构和敏感器故障，考虑故障诊断结果的不确定性与系统参数的不确定性，分别采用H2和H∞范数作为系统故障诊断和容错控制的性能指标，设计输出反馈混合H2/H∞控制律[8]。Fan J H在考虑执行机构饱和限制的情况下，设计了一种鲁棒集成方法[9]，并在无人机控制系统中得到了应用。Wang H[10]针对线性变参数系统以及带有不确定性的线性离散系统，设计了故障诊断与容错控制集成方法，但这两种设计方法只能针对低频故障，对于高频干扰也缺乏鲁棒性，对于快变故障难以达到诊断与容错目的。Zhang Ke在其专著[11]中研究了非线性系统的故障诊断与容错控制的集成设计，但没有考虑建模不确定性的问题，并且采用一致终极有界理论证明观测器的稳定性，使得该方法的实用性受到很大限制。Davoodi[12]针对线性切换系统，在H∞/H2框架下设计了故障诊断与容错控制的集成设计，并通过求解线性矩阵不等式得到系统参数。

本文针对视线制导坐标系下自主交会的轨道控制问题，考虑推力器故障，研究了一种故障诊断与容错控制的鲁棒集成设计方法。

1 故障诊断与容错控制集成设计

1.1 问题描述

实际交会过程中的最终逼近段，追踪飞行器和目标飞行器一般已经处于同一轨道平面内，因此最常用的是两个飞行器在同一轨道平面上的动力学方程。文献[13]给出了任意偏心率轨道上的视线相对运动方程:

(1)

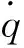
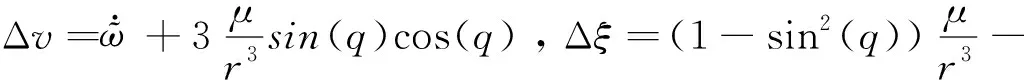
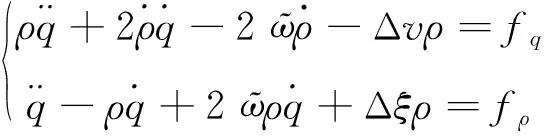
(2)

方程(2)的第1行为视线方向的运动方程,称为纵向运动方程。第2行为视线垂直方向的运动方程,称为法向运动方程。

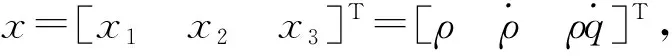
(3)

这是一个含有建模不确定型的非线性系统，

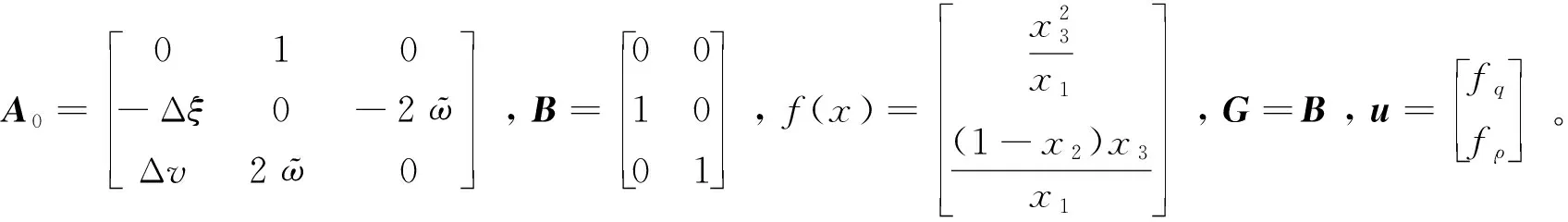
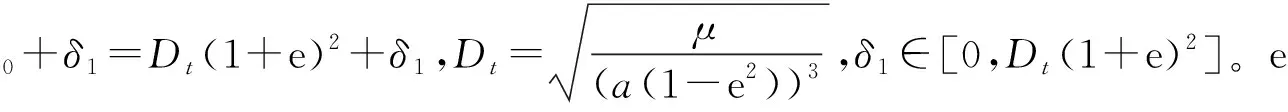
A0=A+ΔA

(4)

动力学方程(2)的不确定性部分ΔA又可以表示为

ΔA=EΔΔFΔ

(5)

在考虑推力器故障的情况下，动力学方程(2)可以表示为

(6)

式中fa(t)表示推力器故障矢量，E为推力器故障输入矩阵，且E=B，C为系统状态的观测矩阵，y为系统状态输出。

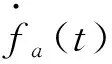
1.2 鲁棒容错控制器设计

对于方程(6)设计故障观测器

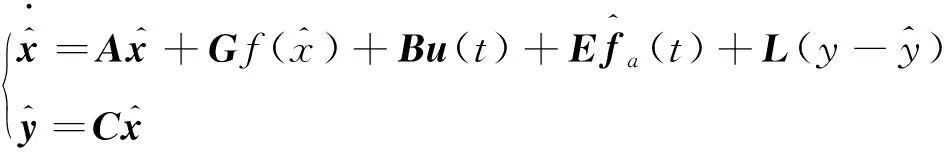
(7)

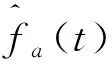
(8)

(9)

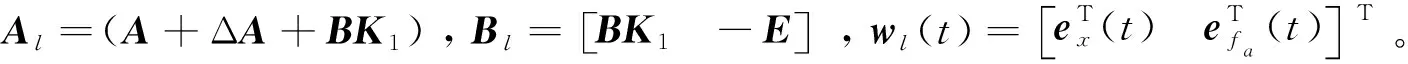
取Zl=Clx，Cl=I作为广义可控输出。则可以得到一个广义线性不确定性系统

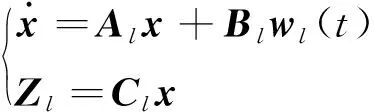
(10)

引理1[14]对于不确定性系统(10)，假设γ1>0是任意给定的常数，则下列2个条件是等价的：

2)存在一个正定矩阵P1，使得下列不等式成立：

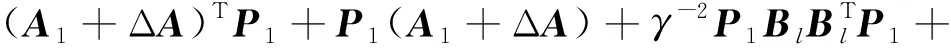
(11)

式中A1=A+BK1。

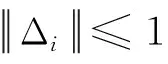
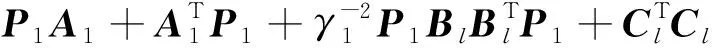
(12)

(13)

式中R0=AX+XAT+BW1+(BW1)T，W1=K1X。

(14)

根据schur正交补定理，式(14)等价于不等式(12)，根据引理1和引理2即可得到定理1中的结论。

1.3 自适应故障观测器设计

设计推力器故障的自适应估计律为

(15)

则系统(10)的状态估计误差为：

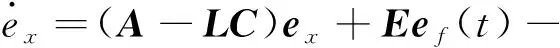
(16)

故障估计误差的动态方程：

(17)

(18)

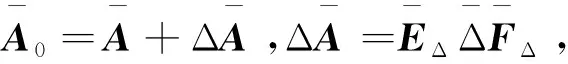
为了分析广义系统(18)的稳定性情况，首先定义一个椭球集并引入两个引理：

(19)

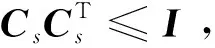
引理4[17]设xs和ys为具有适当维数的向量，则下列不等式成立：

式中Qs是任意具有适当维数的正定矩阵。

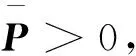
(20)

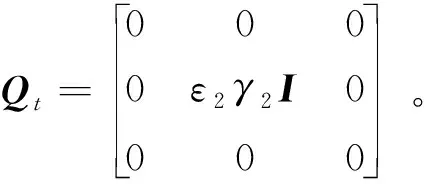
证明. 定义一个Lyapunov函数

(21)

求它对时间的导数可以得到

(22)

(23)

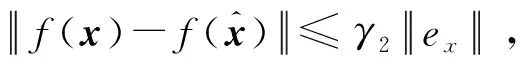
上式又可以表示为：

(24)

结合式(22)～(24)，可以得到

(25)

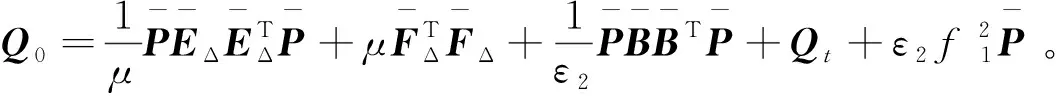
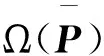
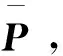
(26)

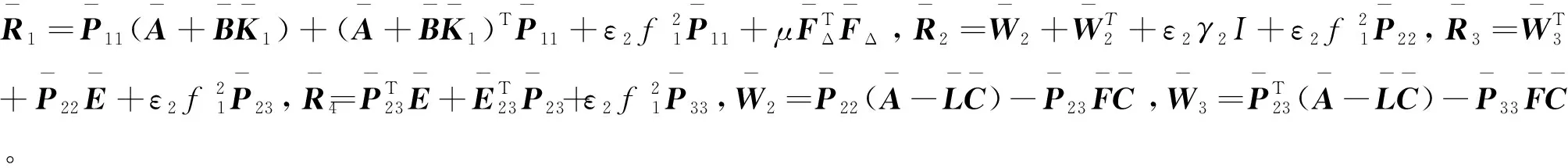
证明.与定理1的证明高度类似，此处省略。

根据定理3可以得出，不确定性系统(10)的状态估计误差ex和故障估计误差efa是收敛有界的。从而故障观测器的参数可以由下式求得

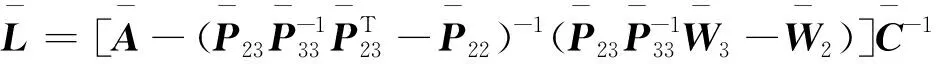
(27)

2 仿真结果

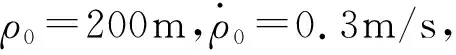
根据定理3，可以求得观测器的参数为：

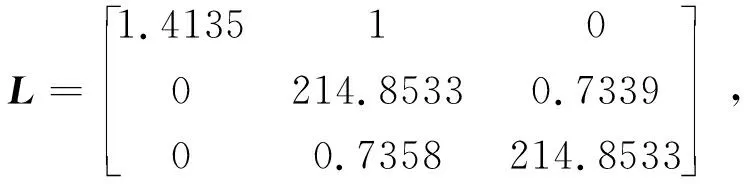
仿真结果如下图所示。图1是无故障发生时，追踪航天器的相对位置变化曲线，可以看出交会过程是稳定的，并且没有超出测量视场等情况发生。

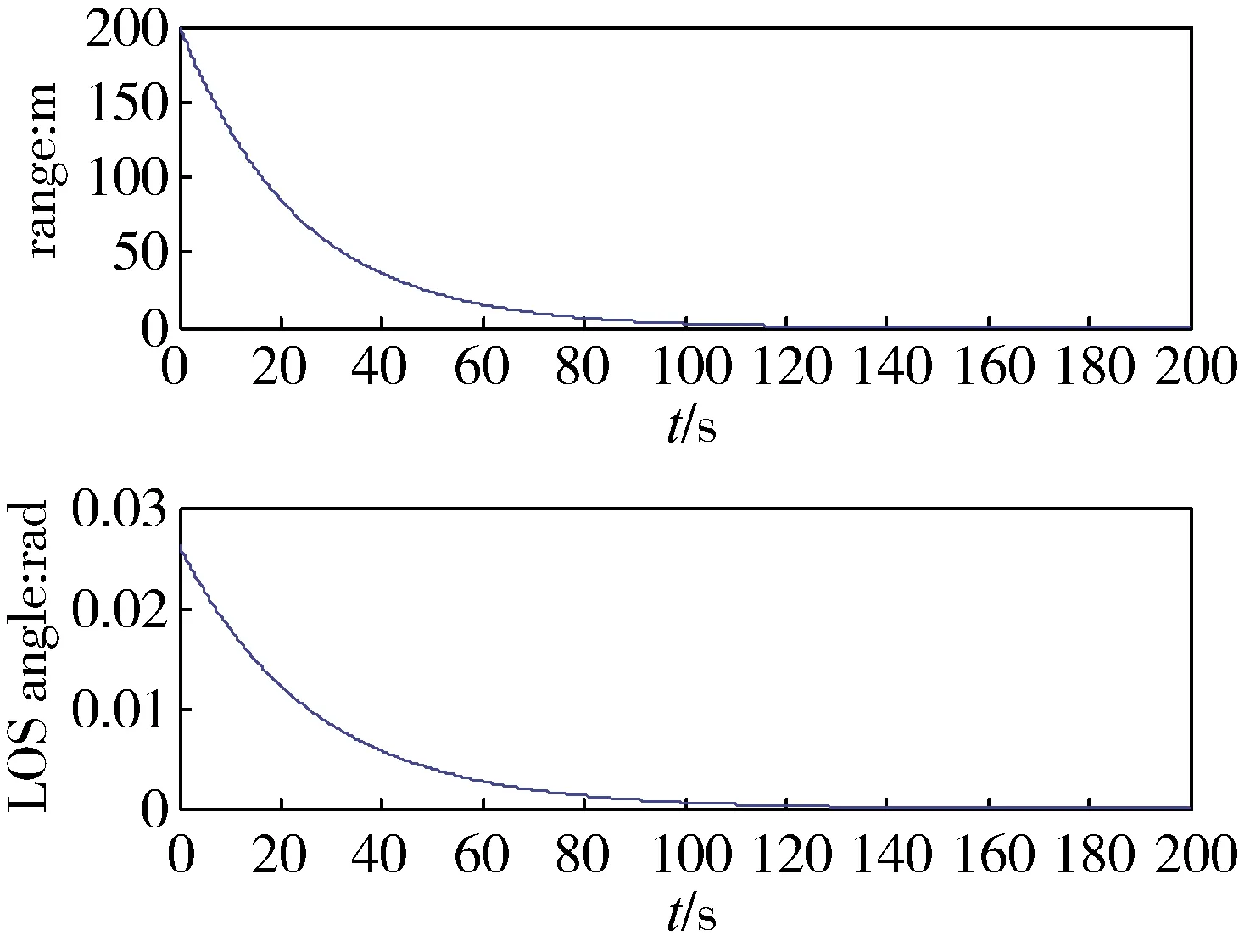
图1 目标航天器和追踪航天器的相对位置

为了更清楚地说明航天器在交会平面内的相对轨迹，本文采用国际空间站的逼近走廊进行说明。

如图2所示，在距离目标星200m～20m之间，逼近走廊以V-bar为中心线，半锥角为8°，在最后20m，逼近走廊以“对接单元口平面”纵轴为中心线，半锥角为4°，图2是无故障发生时的相对轨迹。

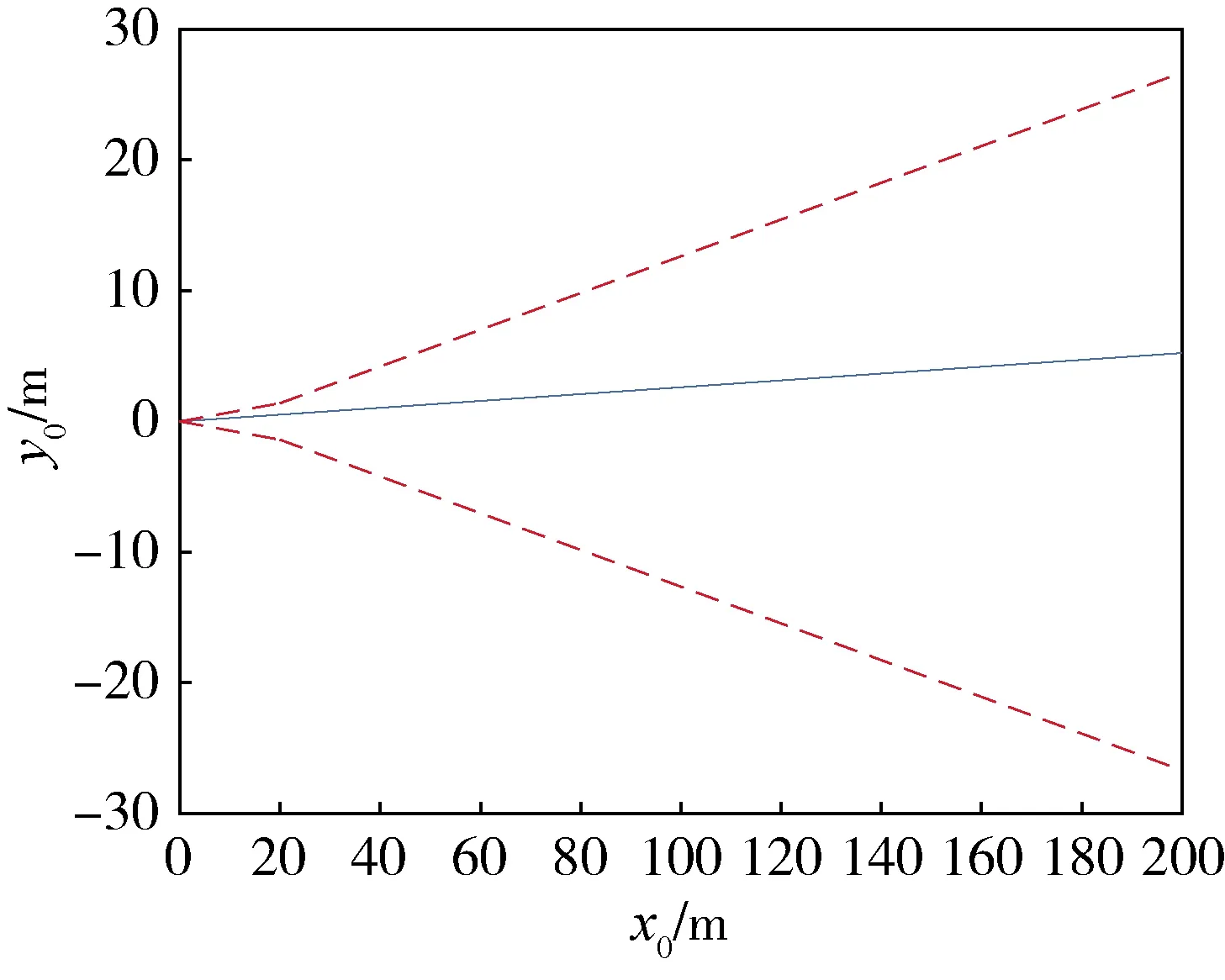
图2 追踪航天器沿逼近走廊的相对轨迹

图3是推力器真实故障与故障观测器的输出曲线，从图中可以看出，故障观测器的输出结果与仿真设定值一致。

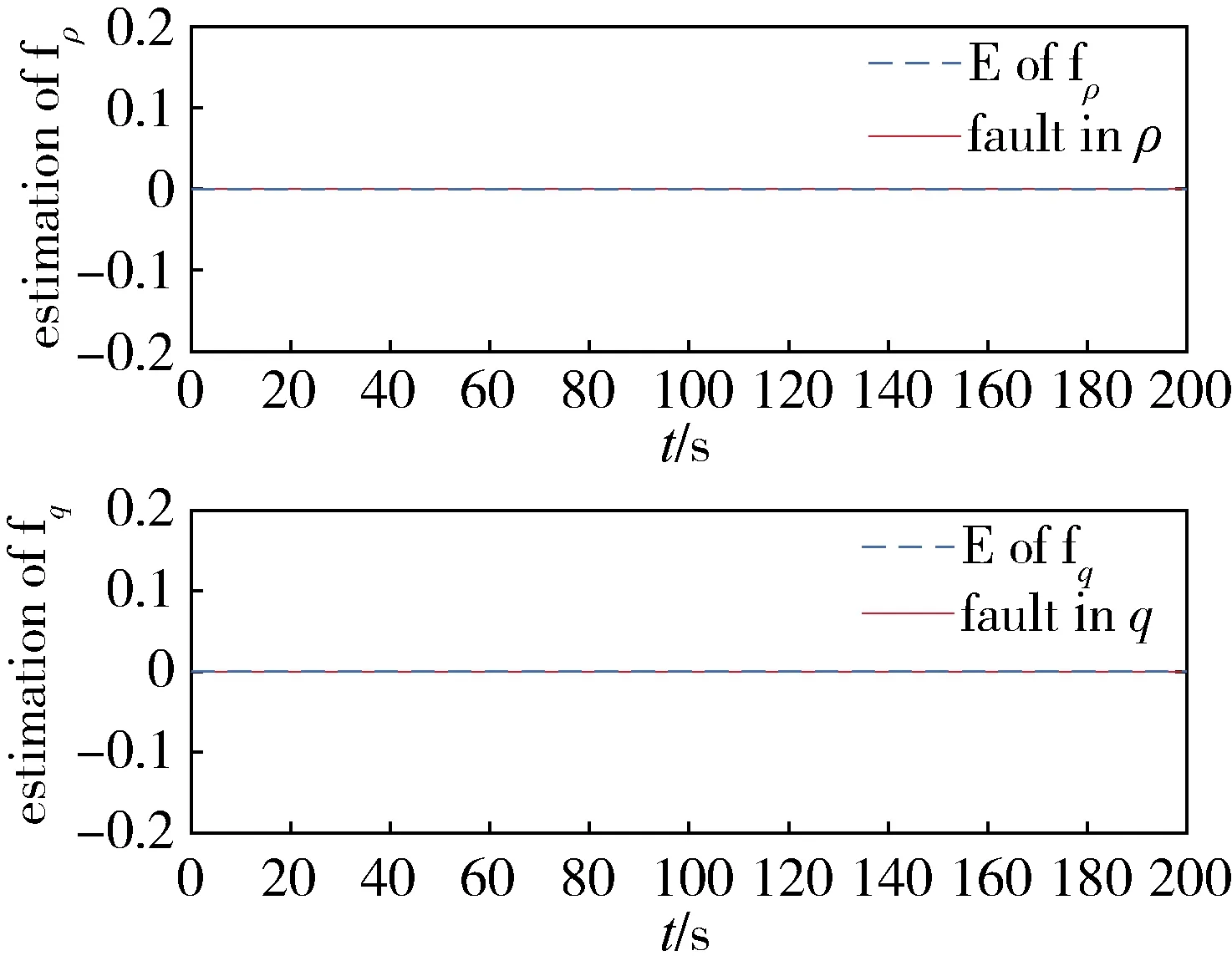
图3 故障观测器对追踪航天器故障的观测结果

假设追踪航天器推力器在10(60s之间发生故障，故障函数用fq=(-0.05sin(0.05πt)-0.05)m·s-2表示。追踪航天器在逼近走廊中的相对轨迹如图4所示。

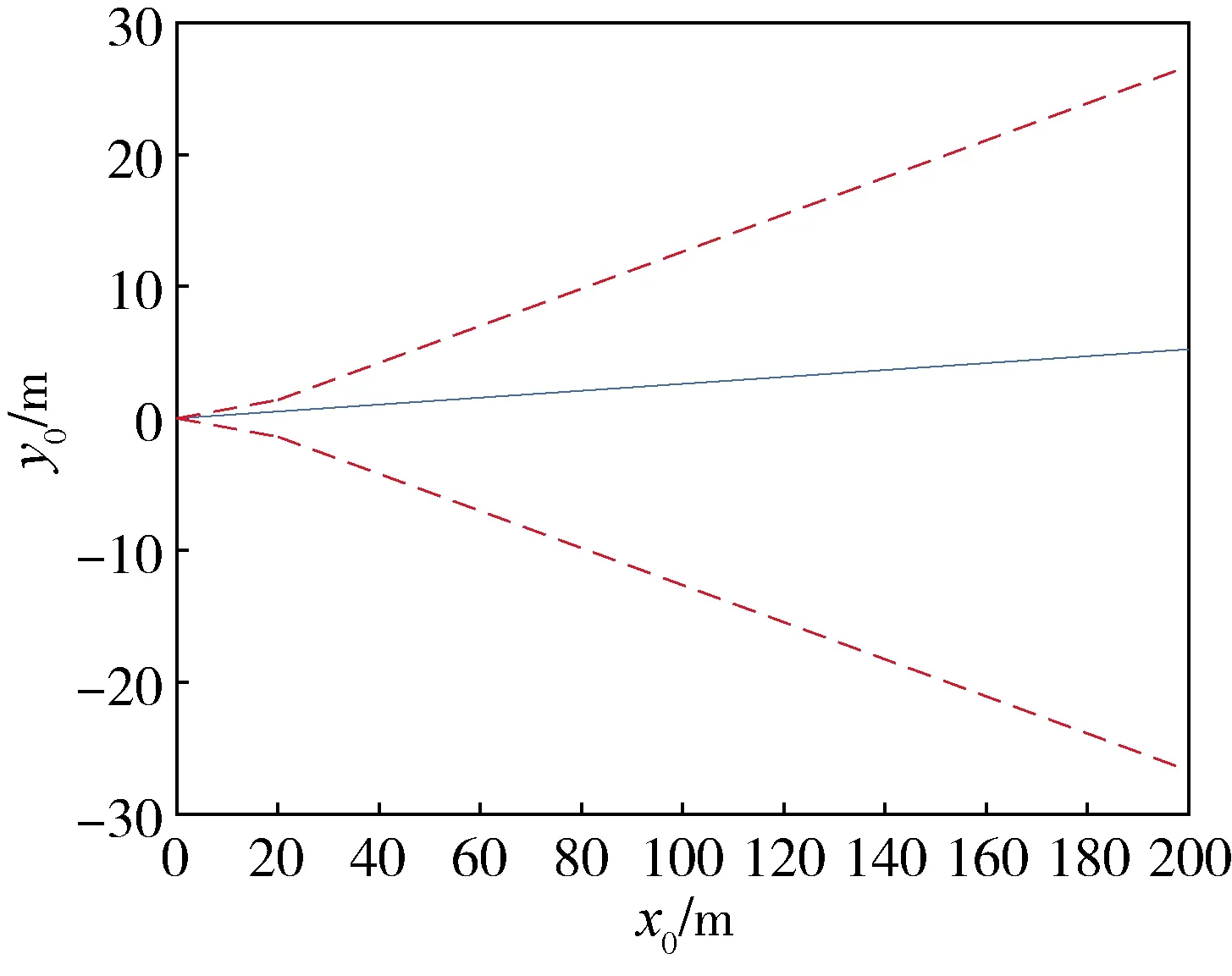
图4 故障情况下追踪航天器沿逼近走廊的相对轨迹

从图中可以看出，追踪航天器沿逼近走廊的轨迹控制仍然令人满意，在故障条件下，追踪航天器没有超出视场或触发避撞机动等情况，为追踪航天器在不影响交会任务的前提下，实现故障单机隔离并切换备份，达到了容错控制的效果。

图5是推力器真实故障与故障观测器的输出曲线，从图中可以看出，追踪航天器推力器发生故障后，故障观测器迅速并准确地估计出故障，估计结果与仿真设定值基本一致。

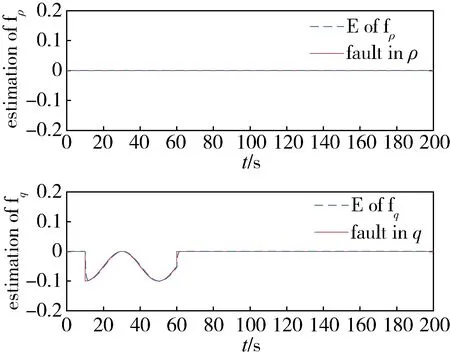
图5 故障观测器对追踪航天器故障的观测结果

3 结论

对于视线制导坐标系下的自主交会问题，本文设计了故障诊断与容错控制鲁棒集成方法。该方法构造简单，便于实现，在追踪航天器发生推力器故障后，能够在保证追踪航天器轨迹安全的同时，迅速准确地诊断并隔离故障。该方法能够提高空间交会的安全性，减少避撞机动等操作的风险，从而提高自主交会的成功率。