基于强化学习的在轨目标逼近*
2021-12-07郭继峰陈宇燊白成超
郭继峰 陈宇燊 白成超
哈尔滨工业大学智能感知与自主规划实验室, 哈尔滨 150001
0 引 言
随着人类对太空的探索和开发,为保证航天器更加持久地在轨运行、提高航天器的自主运行能力的智能化在轨服务技术研究具有重大意义,也是目前国际关注的热点。
在轨服务过程中,提供在轨服务的航天器需要与目标逼近,以便对目标进行抓取和维修等操作,而逼近过程涉及航天器相对运动,包含受控个体的局部运动以及耦合关联的整体非线性运动,并且需要考虑包括安全速度限制和服务航天器敏感器指向约束等诸多约束,这些约束直接导致接近过程中制导、控制难以实现。为了满足日益增长的在轨服务需求,研究给定目标下的在轨逼近问题,对构建通用化在轨服务基础技术体系有重要价值。
根据服务航天器与目标航天器的距离,在轨目标逼近过程大致可以分为远距离导引段、中距离寻的逼近段和近距离末端逼近段,其中近距离末端逼近段起始于与目标距离几百米到几千米的位置,是在轨逼近过程的核心阶段,受到相关研究者的广泛关注。目前末端逼近的研究方式一般是将控制系统分为导航、制导和控制3部分,对每部分单独研究,本文研究的是在导航信息已知情况下的末端逼近制导与控制。
制导方式根据控制力施加方式不同,在轨逼近过程相对制导方法可以分为脉冲制导和连续推力制导。
脉冲制导控制力施加的形式是速度脉冲,通过短期的速度增量改变服务航天器的轨道运动状态,双脉冲制导是比较经典的一种脉冲制导方式,通过2次速度脉冲实现轨道转移,可以分别通过相对运动方程[1]和线性化的Guass运动方程[2]2种方法计算脉冲施加位置和大小,2种计算方式描述的都是同一个问题,区别是基于线性化的Guass运动方程求解可以避免奇异,但只适用于近圆轨道。此外,相关学者基于主矢量理论研究多脉冲转移问题,Sgubini等[3]通过研究同轨道面和异轨道面的转移,指出最优转移次数最大为3。Broucke等[4]以燃料消耗为优化目标,研究N脉冲最优问题,给出了圆-圆、圆椭圆、椭圆-椭圆情况下多脉冲最优求解方法。
连续推力制导是指在逼近过程中服务航天器发动机不关机,持续产生推力的制导方式。经典的连续推力制导主要有LQR[5]和线性规划[6],两者都是线性化设计方法,LQR设计思路清晰但涉及求解复杂的Raccati方程,线性规划可以在诸多约束的情况下求解最优解,缺点是需要针对问题设计专门的数值求解算法,且不利于工程实现。
此外,相关学者直接研究非线性方程,通过自适应算法、遗传算法和模糊控制等[7]算法进行制导算法设计,相比于线性化的算法,消耗的燃料较少,但算法复杂且计算量大,难以直接应用于工程。
在轨目标逼近不仅需要控制服务航天器与目标航天器的相对位置,还需要控制相对姿态保证对接和敏感器对目标的观测等需求,因此相关的研究分为相对轨道控制、相对姿态控制和姿轨耦合控制,其中相对轨道控制常采用基于线性化的LQR[8]和线性规划[9]方法进行轨道机动和保持,需要针对近圆轨道和椭圆轨道设计控制算法,近圆轨道算法仅适用于离心率小的情况,在大离心率的情况下控制精度效果差且易发散;针对椭圆情况的算法以线性时变方程为控制模型,因此为保证控制性能,需要在周期重新计算控制参数,运算量大。此外还有研究者直接以非线性方程为控制模型,采用自适应控制和鲁棒控制等控制算法,在存在系统参数变化和摄动等干扰的情况下仍保证控制精度和系统稳定性。
强化学习(Reinforcement Learning,RL)是机器学习领域内的研究热点,是目前应用效果最为出色的智能算法之一,通过与环境的交互来获取奖励(Reward),同时不断优化策略(Policy),直到获得最优的策略,是解决序列决策问题的有效途径。RL算法在动力学未知或受到严重不确定性影响时,通过学习可以有效地找到系统的最佳控制器。深度强化学习(Deep Reinforcement Learning,DRL)将深度学习的感知能力与强化学习的决策能力相结合,将传统GNC系统的制导与控制合并,直接感知环境信息然后输出控制量,是一种端对端(end-to-end)的感知与控制系统,适合解决复杂系统的决策规划问题。
由于强化学习在处理复杂系统和序列决策上的优势,人们对基于强化学习的智能控制进行了广泛的研究。Zhang等[10]基于DQN设计了一种机械臂控制算法,该算法仅以相机采集的原始图像为输入,在没有任何先验信息的情况下通过学习就实现了三关节机械臂的控制,展现了DRL处理高维状态空间的强大能力。MIT的Linares等[11]对行星表面软着陆问题进行研究,利用强化学习设计了一种整合制导与控制的控制算法,实现由导航输入直接到推力器输出的端到端的控制器。该算法通过奖励函数的形式对约束建模,经过训练使着陆器在着陆过程中满足安全姿态角和姿态角速度的约束,且能优化燃料消耗。Sallab等[12]基于强化学习提出了一种自动驾驶框架,该算法采用循环神经网络整合信息,使得模型能应对信息部分可观测的情况,在仿真环境下能在多弯道路下行驶良好,并且可以与其他车辆进行简单交互。Won等[13]针对机器人参与冰壶运动的场景,对标准的深度强化学习框架进行改进,基于瞬时特征信息对冰壶运动中不可避免的不确定性进行补偿,在现实世界的比赛中以3:1的成绩战胜人类职业队伍,缩小了强化学习训练成果从虚拟训练环境迁移到现实物理世界的鸿沟。在DARPA组织举行的“阿尔法狗斗”模拟飞行对抗赛中,苍鹭系统公司基于强化学习框架设计的人工智能程序以5比0的大比分击败了美国空军驾驶F-16战机的王牌飞行员。此外强化学习还被应用于电网控制[14]、通信安全[15]和无人机编队控制[16]等领域,这些成果表明了在求解复杂非线性控制问题中强化学习有着巨大的潜力和优势。本文针对在轨服务航天器对在轨目标逼近问题开展研究,结合强化学习和控制理论的相关技术知识,设计了一种端到端的整合制导与控制的在轨目标逼近算法,通过仿真对算法有效性进行验证。
1 在轨逼近数学模型
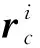
(1)
则服务航天器相对于目标航天器的位置矢量ρ在地心惯性坐标系下满足
(2)
根据矢量求导法则,服务航天器与目标航天器的相对动力学方程在目标航天器轨道坐标系下的形式为

(3)

(4)
进一步整理为
(5)

(6)
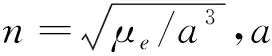
2 基于RL的在轨目标逼近
2.1 算法框架选择
强化学习算法可以分为基于值的、基于策略的和Actor-Critic三类。DQN是经典的基于值的算法,该算法是Q-learning扩展到连续状态空间的结果,通过值函数网络评估动作的好坏,适用于连续的状态空间。该算法引入了经验回放机制和目标网络,极大的提高了训练过程的稳定性,缺点是不能输出连续的动作,若要输出一个区间上的动作,需要将该区间离散化,对控制效果有影响。基于策略的算法不需要维护一个值函数网络判断动作的好坏,而是直接对策略参数进行优化,适用于高维和连续动作空间,可以学到随机策略。Actor-Critic算法结合了前两者的思想,包括Actor和Critic两个网络,Actor网络根据Critic的评判采取行动,Critic网络根据环境的反馈对Actor的行为做评估,借助Critic的反馈,不用等到回合结束,可以单步更新。
DeepMind团队将Actor-Critic与DQN结合提出了DDPG算法,相比于Actor-Critic,DDPG输出动作不是概率分布而是一个确定的值,可以降低在连续空间中探索的成本;相比于DQN,DDPG可以输出连续的动作,在智能控制研究中广泛应用,因此采取DDPG作为空间目标逼近问题的RL算法框架。
2.2 模型设定
相对位置控制的目标是通过观察服务航天器的位置速度等信息,控制发动机推力,使服务航天器向期望位置运动,实现服务航天器对目标的逼近。在确定选取DDPG的算法框架后,需要设计的内容包括观测值、动作、奖励、网络4部分:
1)观测值
观测量的选取应该保证对反映逼近效果的状态量的可观性,从而确保智能体能根据观测的状态输出正确的控制指令。相对位置控制中相对位置和速度是反映逼近情况的关键指标,因此选取的观测量为s=[rv],r和v分别为服务航天器相对于目标的位置和速度矢量,通过在其体坐标系下的三轴分量表示,这样的状态设置能保证智能体可以获取足够的关于逼近状态的信息,保证逼近控制的性能。
2)动作
智能体的动作a=[Fx,Fy,Fz]T,其中Fx,Fy和Fz为三轴发动机推力,考虑硬件实际情况,推力应该满足限幅条件,即
Fx,Fy,Fz∈[-Flim,Flim]
3)奖励值
奖励是智能体判断自身动作好坏的唯一信息来源,好的奖励函数能加快模型收敛,提高策略控制性能。在轨逼近过程中,状态值包括相对位置和速度,由于逼近段起始于km量级,加上速度项,智能体的状态空间很大,奖励稀疏,如果仅在到达目标点时给奖励,模型很难收敛,因此需要设计辅助任务引导模型收敛。此外考虑安全相对速度等限制,相对速度需要随着相对距离缩短而降低,因此辅助任务为跟踪参考速度
(7)


(8)
在智能体的控制下,服务航天器需要尽可能与参考速度一致。此外发动机工作消耗燃料,在实现逼近目标的前提下应尽可能降低燃料消耗,因此奖励函数需要包含燃料消耗带来的惩罚,对应奖励函数形式为
(9)
式中:α为跟踪参考速度精度的奖励评估系数,Isp为燃料比冲,gref为计算比冲所参考的重力加速度,g(·)为速度偏差奖励计算函数,形式为
(10)
式中:β是对燃料消耗速率的奖励系数,这样的奖励函数能使模型尽可能的跟踪参考速度实现目标逼近,同时优化燃料消耗率。
4)网络设计
DDPG算法包括Actor和Critic两个网络,Actor网络输入是六维观测状态,输出是三轴发动机推力;Critic网络输入是由观测值和动作组成的九维向量。如表1所示,Actor和Critic网络都包括3个中间层,采用Relu作为激活函数,为实现推力限幅,策略网络输出层采用Tanh将输出归一化到-1~1之间,结合发动机推力限制经过一个比例放大输出发动机推力。

表1 Actor和Critic网络结构
3 仿真校验
按前述设计方式搭建仿真环境,模型参数设置如表2

表2 相对位置控制DDPG网络设置
为保证训练结果的鲁棒性,初始状态在目标点附近一定范围内随机选择,在MATLAB下搭建仿真环境如图1。
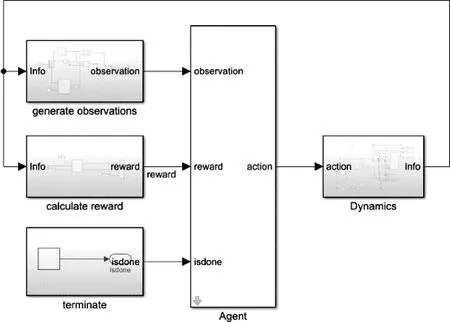
图1 RL逼近控制Simulink框图
其中
训练过程每个回合奖励、平均奖励如图2,随着训练的进行,每个回合获得的总的奖励逐渐上升,经过约1000回合的训练模型基本收敛,停止训练。

图2 RL位置控制模型训练过程
设置初始状态s1:
[x0,y0,z0]=[600,500,400]m
[vx0,vy0,vz0]=[0,0,0]m/s,
和s2:
[x0,y0,z0]=[-700,600,200]m
[vx0,vy0,vz0]=[0,0,0]m/s
在训练得到的智能体控制下,服务航天器逼近过程轨迹如图3(a)和图4(a),可以看到服务航天器最终到达目标点并稳定在该处,图3(b)和图4(b)为相对位置的分量。从图3(c)和图4(c)相对速度分量可以看到,在距离较远的时候,服务航天器以较快的速度逼近目标点,但随着与目标点距离越来越近,服务航天器的相对速度逐渐降低,到达目标点后趋近于零,满足逼近过程的安全要求。可以看到经过训练,服务航天器能逼近目标,最终稳定在目标点附近,并且随着相对距离减小,相对速度也逐渐降低,满足逼近过程的安全性要求。
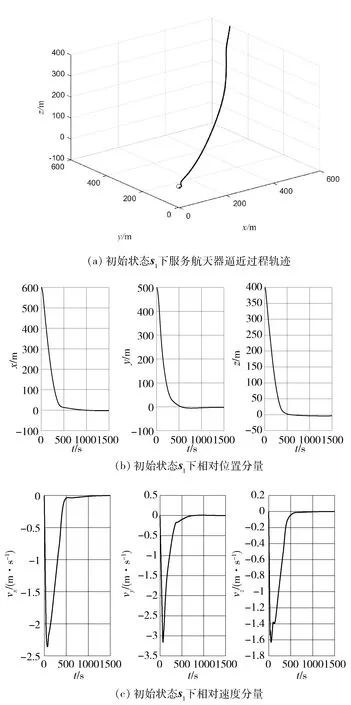
图3 初始状态s1下逼近过程
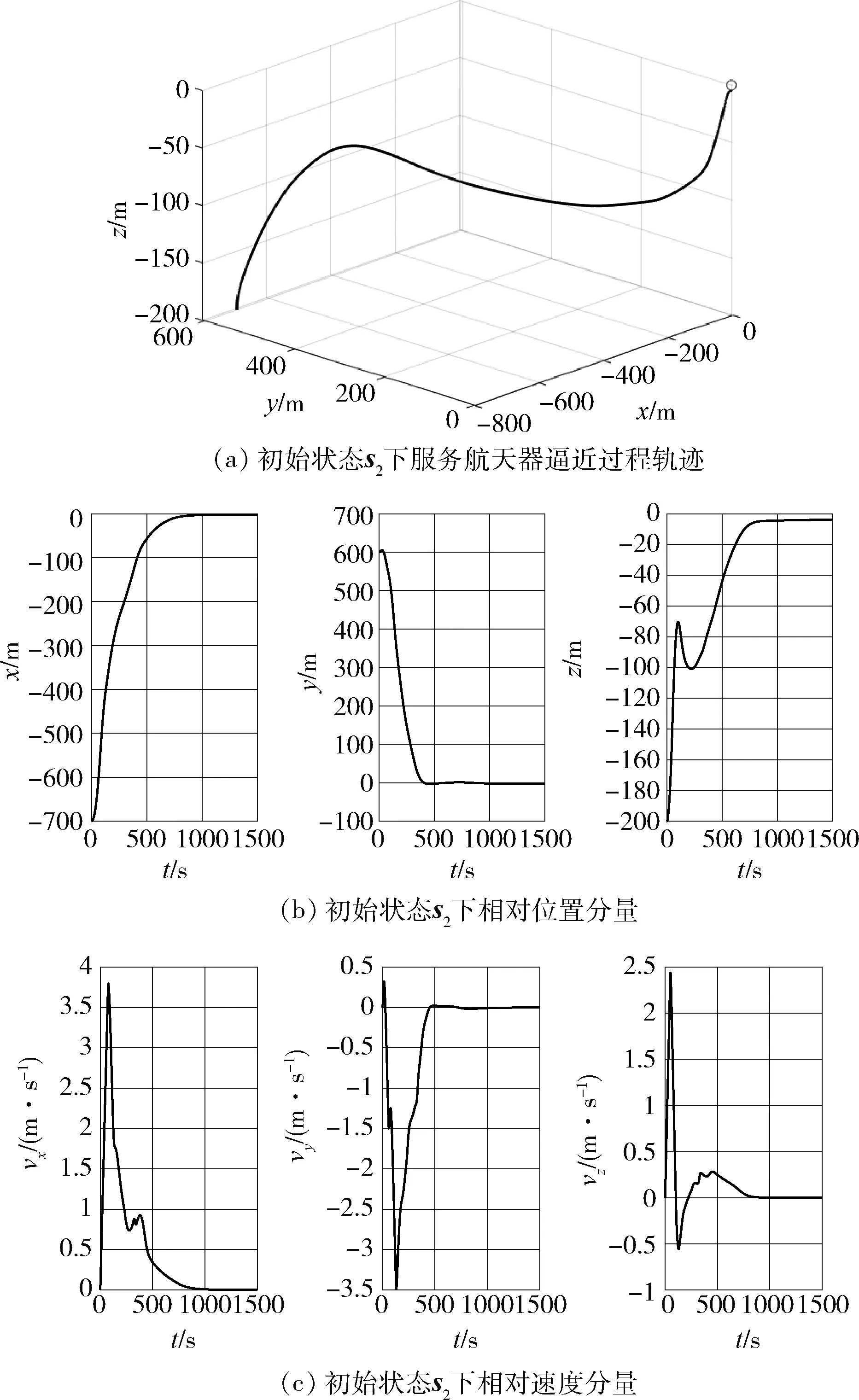
图4 初始状态s2下逼近过程
在状态s1下,分别基于RL和LQR的逼近过程燃料消耗曲线如下

图5 初始状态s1下RL控制燃料消耗情况

图6 初始状态s1下LQR控制燃料消耗
可以看到基于RL的算法和基于LQR的逼近控制分别消耗燃料质量57.82kg和64.59kg。两者的燃料有一半消耗在前100s内,这是因为服务航天器由初始的相对静止到逼近所需一定的相对速度,需要发动机推力加速,消耗了末端逼近的大部分燃料。
设初始状态x0,y0∈[-1000,-600]∪[600,1000]m,z0∈[-300,300]m,通过300次实验,对比相同初始状态下基于RL的方法和基于LQR的控制方法所消耗燃料的质量,其中118次基于RL的方法燃料消耗率低于基于LQR的方法,其他情况下基于LQR更省燃料,即两种算法相比另一种优势并不明显,这是因为基于强化学习引入了参考速度,因此本质上学习得到的是一种控制算法,而引入的参考速度是制导信号,制导方案对燃料的影响较大,因此基于RL的方法在燃料消耗上的优势并不明显。由于问题特点,为保证逼近过程的安全性要求,参考速度是必要的。
4 结 论
针对在轨目标逼近问题进行了研究。首先介绍了在轨目标逼近过程和基于强化学习的控制研究现状,然后对在轨相对运动进行建模,接着基于DDPG强化学习框架设计了端到端的逼近控制方法,通过引入参考速度解决了奖励稀疏和安全性问题,最后通过仿真实验,将基于强化学习的逼近算法与基于模型的LQR逼近控制方法进行对比,基于强化学习的逼近控制算法不依赖模型,可以在没有系统模型或模型复杂的情况下,通过学习实现在轨目标逼近;由于引入了参考速度,在燃料消耗方面,相比于LQR控制算法,基于强化学习算法的优势并不始终保持。
