基于抗差估计改进的GNSS/INS组合导航完好性监测方法*

任利简 赵修斌 庞春雷 张 闯 张 良

1. 空军工程大学信息与导航学院， 西安 710077 2. 中国人民解放军95510部队， 贵阳 550029

0 引 言

卫星导航系统完好性是指当系统无法完成预定操作或对导航结果不信任时，向用户及时发出有效告警的能力[1]。对于用户来说，最直接、便捷的完好性监测方法主要有接收机自主完好性监测[2](receiver autonomous integrity monitoring, RAIM)和用户辅助的完好性监测(user assistant ingtegrity monitoring, UAIM)。其中，对于飞机、舰艇等运动载体来说，惯导(inertial navigation system, INS)辅助的GNSS(global navigation satellite system, GNSS)完好性监测(INS assistant GNSS integrity monitoring, IAIM)在性能上具有优势[3]，并且已经得到了广泛应用。

目前GNSS/INS组合导航系统通常使用卡尔曼滤波，IAIM方法也大多是建立在卡尔曼滤波残差检测的基础上。作为IAIM的关键技术，传统的残差卡方检测法可以较好地检测出突变误差，但当GNSS或INS出现缓变误差时，由于初始误差不易检测，有故障的输出将影响下一步的状态估计值，使其连续跟踪故障输出，导致残差一直保持较小值，难以被系统检测到，影响系统向用户发出及时有效的告警；而Diesel等人于1996年提出的自主完好性监测外推(autonomous ingtegrity monitoring extrapolation,AIME)法[4]在残差卡方检测的基础上，加入了滑窗检测，在检测过程中同时利用当前量测信息和历史序列信息，对于缓变误差具有较好的检测性能[5]。但由于AIME法存在检测时延，不能在误差结束后迅速停止告警，一定程度上造成了漏警率和误警率的上升，影响卡尔曼滤波精度。由此可见，AIME法还有进一步提升的空间。

针对AIME法的上述缺陷，本文在GNSS/INS紧组合和卡尔曼滤波模型的基础上，通过构造标准化残差对观测量进行检测，同时引入IGGⅢ权函数抗差估计进一步提升系统对缓变误差的检测性能，通过对当前历元标准化残差的判断，选择相应的检测方式，以提高组合导航系统完好性的监测效率。

1 GNSS/INS紧组合导航模型

GNSS/INS紧组合系统是建立在卡尔曼滤波基础上、在伪距、伪距率、多普勒或载波频率级别上的组合[6]，当短时间内可见卫星数少于4颗时，组合系统仍然能够保证一定的连续导航能力，避免了惯导单独工作时误差积累过快的问题，因此本文选择紧组合导航系统作为惯导辅助GNSS完好性监测技术的基础模型[7-8]。

1.1 系统状态方程

紧组合系统状态方程包含INS误差方程和GNSS误差方程[9]，其中INS误差方程主要是姿态、速度、位置以及惯性器件误差方程[10]，即

(1)

式中,FI(t)为系统状态转移矩阵，GI(t)为系统噪声转移矩阵，WI(t)为系统噪声矢量，来自陀螺和加速度计的随机误差。XI(t)为15维误差状态变量，其表达式为[11]

(2)

GNSS误差参量为等效时钟误差相应的距离δtu和等效时钟频率误差相应的距离率δtru，其状态方程为

(3)

式中：τtru为误差相关时间，ωtu为白噪声，ωtru为驱动噪声。

对式(1)和式(3)进行联立，即可得紧组合系统状态方程

(4)

1.2 系统量测方程

紧组合系统量测方程包含伪距差方程和伪距率差方程。

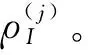
(5)

(6)

同理可得，伪距差率方程为

(7)

对式(6)和式(7)进行联立，即紧组合系统状态方程[12]

(8)

2 基于抗差估计改进的完好性监测方法

2.1 自主完好性监测外推(AIME)法

传统的残差卡方检测法对于缓变误差的检测并不十分有效，因为初始误差很小以至于难以被检测出来，当前历元的故障输出将继续影响下一历元的状态一步预测值，并导致误差连续跟踪输出，使得各历元的残差均保持较小值。

AIME法的出现较好地解决了残差卡方检测法对于缓变误差检测效果不佳的问题。AIME法在残差卡方检测法中引入滑窗检测法，而滑窗检测法的检验统计量不局限于当前历元的观测量，还取决于滑动窗口内的过去历元的观测量[13]。在离散化卡尔曼滤波过程中，k历元的残差rk及其方差Vk分别为

(9)

(10)

定义检验统计量为

(11)

其中

(12)

(13)

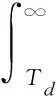
(14)

其中Td为检测门限，可通过上式求得。通过比较检测统计量savg与检测门限Td，如果savg大于Td则表明存在误差，否则无误差。

由式(14)可知，当误警率α确定时，检测门限Td与可见卫星数n之间存在一一对应的关系。若设置α=0.001，则检测门限Td与可见卫星数为n之间的对应关系如表1所示。

表1 检测门限与可见卫星数的关系

2.2 抗差估计改进的AIME算法

作为目前主流的完好性监测方法，虽然AIME法对于缓变误差的检测有较好的作用，但在未检测到小幅误差时，全程基于滑动窗口检测的AIME法仍需考察过去历元的观测量来对当前历元做出判决，使得系统计算负担较重；且在误差产生和结束历元，系统对当前历元观测数据的分析会受到过去历元观测数据的“抑制”作用，从而造成系统当前历元产生误判从而对系统当前历元产生误判，一定程度上提高了漏警率。

为在AIME法的基础上进一步提高组合导航系统对缓变误差的检测效果，本节分别定义了基于当前历元的检测和基于滑动窗口的检测下的标准化残差，并以此引入三段权函数抗差估计对AIME法进行改进。

当基于滑动窗口检测时，定义其对应的标准化残差为

(15)

同理，当基于当前历元检测时，定义相应的标准化残差为

(16)

三段抗差等价权函数表达式[14]为

在这里会好的，我想什么时候照镜子就可以尽情地照。我可以和克里斯蒂娜交朋友，可以把头发剪短，可以让别人去打扫收拾他们自己的残局。

(17)

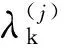
利用三段抗差等价权函数对观测噪声方差阵Rk的对角线元素进行处理

(18)

(19)

3 仿真校验及结果分析

为验证本文所提出的GNSS/INS组合导航完好性监测方法的性能，利用多种实验设备搭建一套仿真平台，包括飞行轨迹生成系统、GNSS信号模拟源、GNSS/INS紧组合卡尔曼滤波系统以及完好性监测模块等，通过设置目前主流的AIME法为对照组，验证所提方法的有效性。

仿真过程中GNSS输出频率设为1Hz，惯性测量单元的输出频率为100Hz，陀螺随机常值漂移为0.1(°)/h，加速度计随机常值漂移为10μg，可见卫星数为10颗(S1～S10)，卡尔曼滤波周期为1s，仿真时间为1600s，伪距观测噪声为1m，滑动窗口数设为5，误警率设置为0.001。

测试1：设8号卫星的伪距观测量在第201s出现幅值为20m、持续59s的突变误差，测试结果如图1所示。

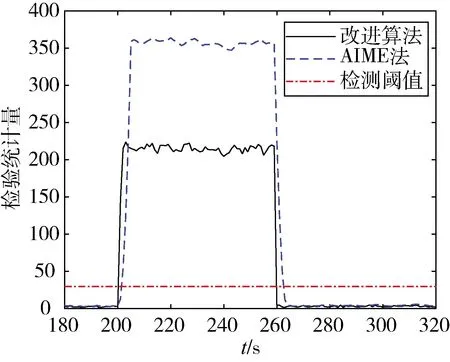
图1 突变误差下两种方法检验统计量的对比

可以看出，当第201s注入误差后的短时间内，两方法的检验统计量均明显增大，且均大于检测阈值，说明两种方法都能检测到突变误差。但同时也可以发现，本文所提出的改进方法相较于AIME法，不仅能够更迅速地检测出突变误差，还能在误差消失后迅速恢复正常的检验统计量，避免了错误告警。

测试2：设6号卫星的伪距观测量在第201s出现速率为1m/s、持续19s的缓变误差，测试结果如图2所示。

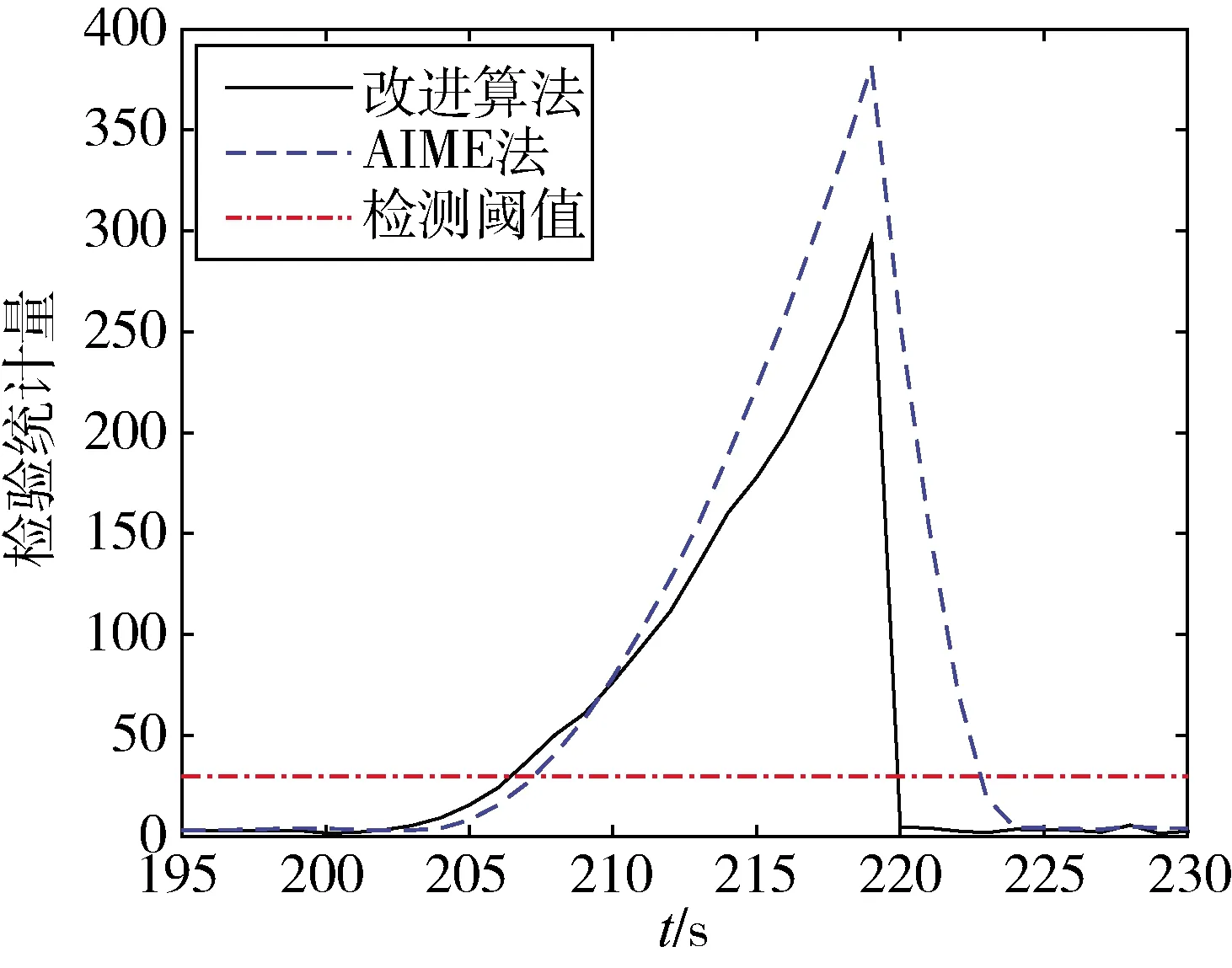
图2 缓变误差下两种方法检验统计量的对比

由图可知，对于缓变误差，本文所提出的改进方法同样能够更快速地将其检测出来并发出告警，并在误差消失后1s内迅速停止告警，而AIME法则需要4s才能恢复正常检验统计量。这是因为本文所提改进方法在误差消失后能够迅速转换检测方法，将基于滑动窗口检测切换为基于当前历元检测，避免了之前历元的观测量影响当前历元的检测过程、得出错误的检测结果。

测试3：设6号卫星的伪距观测量在第171s先出现速率为1.5m/s、持续19s的缓变误差，然后在第195s出现幅值为20m、持续55s的突变误差，再在第253s出现速率为3m/s、持续8s的缓变误差，最后在265s出现幅值为10m、持续3s的突变误差。测试结果如图3所示。

图3 间歇性误差下两种方法检验统计量的对比

可以看出，在出现间歇性误差的情况下，AIME法因为自身检测的“时延”特性，很容易造成误判，向用户发出错误的告警信息；而本文所提出的改进算法由于没有全程基于滑动窗口检测，能够灵活采取对应的检测方法，所以在一定程度上避免了误警。

4 结 论

本文所提方法在建立GNSS/INS紧组合模型以及现有的AIME法的基础上，利用三段抗差等价权函数对卡尔曼滤波过程进行调整，进一步消除了缓变误差的影响；并通过对当前历元观测量的检测情况决定下一历元的检测方法，较好地克服了AIME法全程基于滑动窗口检测而造成的告警时间长等缺陷。通过对比试验，验证了所提方法的有效性，从而为卫星/惯性组合导航系统的完好性监测提供了另一种可行的方法。