基于天然气管网的可压缩流模型与应用

胡代平

(上海交通大学 安泰经济与管理学院,上海 200030)

在人类社会发展历程中,流是人们对自然界中一类具有移动特性事物产生认知而形成的一个基本名词。简言之,人类最早从流动的水中认识到运动的事物就是流。因此,流是一个古老的名词,但同时又是一个永恒且被广泛使用的概念,在人们的日常生产与生活当中,流早已处于十分重要的地位。

现代科学中有关“流”的概念几乎是无处不在的。在物理学中,带电粒子的有规则运动被称为电流;在工程学中,与固体相对应的物体形态被称为流体;在计算机科学中,一些特定的二进制数序列被解读为命令流、数据流;在道路交通领域,人们把车道上往来不息的车辆称作车流;在经济活动中,又有随处可见的资金流、商流、物流、信息流等事例。随着应用的普及,人们对流的研究逐渐扩展。

在流体力学研究方面,求解可压缩流的Godunov类型黎曼解法器的研究吸引了大量计算流体力学研究人员的关注[1]。近几十年来,根据方向分裂的设计思路,出现了广泛应用于流体力学的数值计算,例如中心格式、通量差分裂格式[2]、通量向量分裂格式[3]、HLL 类格式和AUSM 类格式[4-10]等。这些数值方法虽然取得了可用结果,但在计算网格界面数值通量时,只考虑了法向的波系,忽略了横向波系的影响[11],在求解多维问题时,不仅会降低格式的分辨率,而且稳定性能减小,进而影响格式的计算效率[12]。为弥补这些数值算法上的不足,研究人员进行了针对性的改进。Rumsey等[13]将多维性引入到一维Roe黎曼解法器中从而获得一种线性化的多维Roe格式、Colella提出了多维角点的输运格式、Le Veque[14]设计了多维波传播算法。

在风洞流场研究方面,一些学者分别采用激光多普勒测速技术、瑞利散射测速技术和粒子图像测速技术等光学测量方法对可压缩流湍流度进行直接测量,取得了一定成果[15],但由于光学测量方法普遍频响不高,难以捕捉到速度脉动中的高频成分。还有学者通过引入压力脉动项从理论上优化湍流度求解方法,用以准确评估高速风洞可压缩流湍流度[16]。

在可压缩流体的数值研究方面,传统的有限元数值方法仍常见于模拟现实工作中,但由于其计算量庞大而难以获得理想结果[17-23]。对此,基于可压缩流的流动特征,利用多尺度方法对其进行数值模拟的多尺度混合有限元法出现了[24]。多尺度有限元法具有节省计算量的显著特点,同时在粗网格上满足局部守恒,适于处理复杂地层以及多相相流问题。

总之,上述研究侧重于流的“流速”“流体压力”等物理方面的属性分析,极少涉及“流量”“流向”等应用方面的探索。

1 问题描述

在现实中,“网络”与“流”一样也是一个永恒且被广泛使用的概念。一般而言,网络是指彼此连接的一组实体组合,并在确定规则下,允许实体之间进行物质或非物质元素的输送或传播。根据所涉及的实体类型,网络术语也有所不同。例如,交通网络是基础设施和用于运送人员和货物的不同地理区域之间的车辆组合;电话网络是用于传输语音信号的基础设施组合;神经网络是一组彼此连接的脑细胞组合;计算机网络是一组计算机链接到与物理线路彼此交换作为数字数据的信息等。传播的元素是流动的,由此可见,“网络”与“流”是不可分割的伴生概念,进而形成了网络输送问题。

在网络输送问题研究中,无论输送的是何种元素,都可以被视为是流的输送。例如,水管输送的是水,电路输送的是电,以天然气为代表的气体也可以通过管道输送。在数理研究中,所有这些形态都可以忽略其自身物理性质而被抽象为流。在传统的网络模型中,当一股或多股“流”流入一个节点时,节点不会对流量产生影响,即不论流入节点的流量为多少,流出节点时的流量均与流入节点时的流量相同,不妨称之为节点的平衡规则。显然,在现实中,有些流并不服从平衡规则。例如,在实际油藏中,流体都是可压缩的,不可压缩流只是一种理想化的状态。因而,在天然气管输网络中,连接上下游两个压气站之间管道的流出端与流入端的输气量通常是不相等的,在压气站这种“节点”上的表现就是不服从平衡规则。此外,还有河道中的水流流经水坝时,由于水坝的拦截及流量调节作用,流出水坝的流量也可能与流入水坝时不同。因此,传统的网络模型在解决这种不服从平衡规则的流输送问题时会有偏差,需要采用新的思路。

天然气作为最环保的能源之一,已成为世界各国的首选能源。近年来,我国天然气的消费量保持持续增长的态势,已是全球天然气消费大国。据统计[25-26],2015年我国天然气消费量为1 932亿m3,2016年为2 058亿m3,同比增长6.5%;2017年我国天然气消费量达到2 373 亿 m3,同比增长15.3%;2018 年我国天然气消费量达到2 803亿m3,同比增长18.1%;2019年我国天然气消费量达到3 067亿m3,同比增长9.4%;2020年我国天然气消费量约3 200亿m3,同比增长4.3%。同时,天然气运输的昂贵成本、危险性高也是全世界都极为关注的问题。目前,世界上大规模输送天然气的方式基本上有两种:管道运输和液态运输。我国采用的是以管道运输为主的天然气运输方式。

受益于天然气消费量的增长,我国天然气管道长度逐年增长。过去10年间,随着我国社会经济的快速发展,掀起了骨干管网建设的新高潮。目前,我国已建成西气东输管道一、二、三线,陕京系统、涩宁兰、中贵、中缅、川气东送、秦沈、哈沈等多条大口径的天然气长输管道(沿线设有多个压缩机站),以及用于大区域资源调配的中贵联络线和冀宁联络线两大跨省联络线工程。已经形成“西气东输、海气登陆、就近供应”的网络格局。

在网络格局中,天然气管网具有输气管网线路长、输气量和运输周转量大、气源多、分输点多、压缩机站多、连接线中气体的流动方向不确定以及不同管道的压力等级不一致等一系列特点,这些特点极大地增加了天然气管网运行管理的工作量与难度,仅凭调度人员的经验做出的判断很难全面并且有效地应对管道运行过程的调度管理问题,更难以实现管网的优化运行。此外,管网在服役期内每年都要花费大量的保养和维护费用。天然气长输管网的能耗也非常大,据统计,国内天然气管道燃气耗用量(不包括机组电耗量)约占输气量的1.5%,这从一个侧面反映了研究天然气管网优化运输问题的巨大意义。

本文从网络最小费用流角度研究天然气管网的最优输送问题。为此,将天然气管网中的气源地、分输点、压缩机站等抽象为一个个的“节点”,将节点之间的管道抽象为“弧”(或称为带有方向的边),同时,将分摊在各弧上的保养、维护、能耗等成本抽象为“费用”,从而有一般常见的最小费用流模型:

通常将网络中的节点记作vi,则式(1)中:s表示天然气源;t表示用户或储气站;fij、bij分别表示弧(vi,vj)上天然气的流量及单位费用;cij表示弧的流量限制。

从实际情况看,天然气在管网中的可压缩性以及流向的不确定性限制了上述模型不可能直接用于解决天然气管网的优化运输问题。因为模型中∑fij-∑fji=0意为网络中任一节点的净流量(节点的合计流出量减去合计流入量)均为0,而天然气的可压缩性迫使各节点的净流量并不一定为0。为了突破模型限制,本文通过增加虚拟节点及相应的约束条件以解决可压缩流的计算问题。

一方面,增加一个虚拟节点D(称为“汇”)。因为天然气管网中节点(主要指压气站)的进气量不小于出气量,所以D可用于承接各节点进、出量之间的差值。另一方面,增加各节点指向虚拟节点D的虚拟弧,用于计算各节点的流量差值,同时也规定了天然气的流向。从理论角度克服了天然气管网输送中的可压缩性及流向不确定性限制,结果如下式所示:

求解上式一般采用内点法,该算法的时间复杂度是多项式复杂度,具体为O(n3.5L),其中,n为变量的个数,L为问题编码的Bits位数。

实际上,天然气管道输送是很复杂的,其复杂性主要表现在压缩机的效能和能耗与输送量的关系是非线性的。但是,从统计的角度分析,这些非线性呈现的关系比较稳定,可以通过离散化方法,将变化区间分为若干段,而每一段内的数据都可以看作是线性的,然后用加权方法对分段数据进行加权平均,加权平均值可综合表现在管线输送的单位价格当中。因此,在宏观上,管网中的天然气输送量与输送单价之间的关系可看作是线性的,所以式(2)适用于管网优化输送问题。

2 算例分析

近年来,某天然气管道公司所辖天然气管道能耗支出占运营费用成本比例不断增大,途经地区的电力政策日趋复杂,影响运营支出的各方面因素难以进行简单平衡,优化电力、燃料及管输收入与支出方案的需求矛盾日益突出。同时,在生产运行中,压缩机启运台数与各管道转输、管输量及销售量息息相关,且燃驱、电驱机组的费用支出与气价、燃料气实际输送距离、当地电价、电力政策及奖惩方法等均有关系。因此,天然气管网的优化输送占据了公司管理工作的突出位置。

该公司管辖网络计有6条管线共计61个站点,其拓扑关系如1图所示。

在实际生产中,影响天然气输送价格的因素众多。其中占据主导地位的是天然气输送量,进而涉及压气站的压缩机启运台数,它与各管道转输、管输量以及销售量息息相关,且燃气驱动机组、电机驱动机组的费用与天然气价格、天然气实际输送距离、当地电价、电力政策及奖惩方法等均有关系。为了适于模型计算,必须对相关因素进行简化和抽象。经统计,该公司现有管道的设计容量及按月计算的输送单价如表1所示。表中A1、B1、C1等符号表示公司管网中各压气站或输气站,每一对上、下游站点即表示两站点之间的输气管线,设计输量表示相应管线的最大输气量。

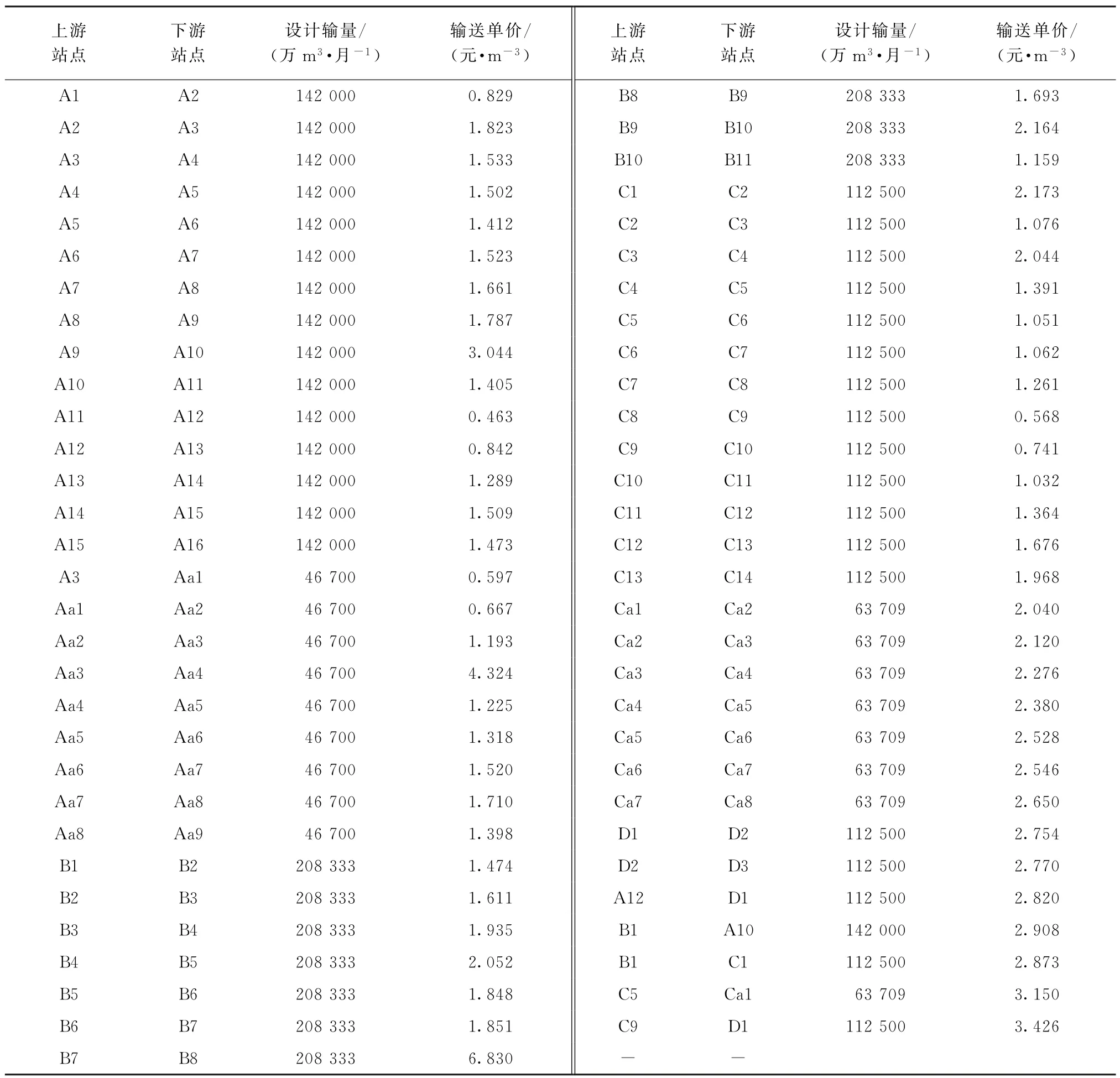
表1 公司管网基本数据

为了运用式(2)进行天然气的优化输送,即寻求满足各节点需求前提下使总输送费用最低的调配方案,假设一个虚拟节点并记为T。显然,各节点至T的弧即表示节点的需求量。已知公司某月需求量与供气量分别为375 837.615 万m3和345 571万m3。通过计算,可知最低总费用为57 754.182万元。各节点需求量及相应管线的流量分别列于表2、3。

表2 公司各站点某月需求量

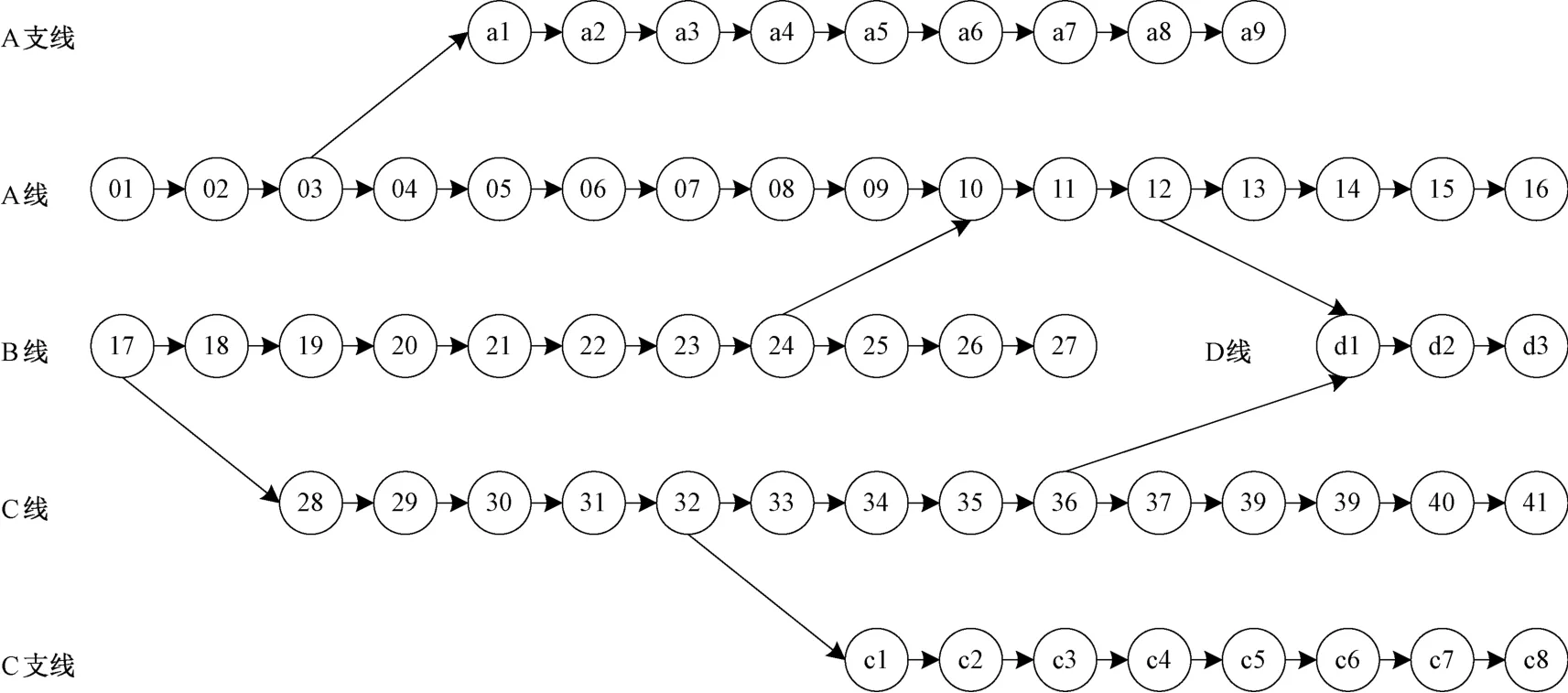
图1 天然气管道公司管网示意图

表3 公司管网优化运行结果

很显然,需求量(375 837.615万m3)与供气量(345 571万m3)之间存在302 66.615 万m3的缺口,填补这些缺口的供气量正好来自因天然气可压缩性而产生的“管存”,具体分配如表4所示。

表4 公司管存分配结果

3 结语

从目前已发表的文献来看,由于管网中天然气流向的不确定、长输管线维护以及压缩机消耗等诸多因素的重要影响,并没有一种含括所有问题的理想的理论研究成果。从天然气管道公司的生产现实来看,保障安全生产是第一位的,有关工程技术应用的研究优先,而结合经济指标的优化研究没有实质性的进展。因此表明,天然气管网优化输送在理论或应用方面都具有极大的研究空间。对于企业而言,本文的研究意义及有效性主要体现在:

(1)在不增加任何附加投入的前提下,可以充分现有的线性规划理论及方法,通过输气方案的调整以实现生产成本及能耗的降低,增强管理提效的理念、提高能源综合利用效率。

(2)在实际销气数据的支持下,通过“以销定产”的营销模式确定天然气的输量分配,提供管网优化运行的合理化建议,将节能降耗目标落在实处,实现天然气管网优化输送的良性循环。

总体讲,目前尚未见到完美的可压缩流优化输送模型。研究过程发现,一般常见的意图实现可压缩流优化输送的思路可概括为“近似模拟”和“类比优化”。近似模拟意为用相关技术系统软件,生成流的多种输送运行方案,通过比较而选出一个成本最低的方案。类比优化意为在客观条件基本相同的前提下,通过对历史记录或同类流的数据对比而选择一个输送方案。

本文在已知网络汇(对应于需求端)流量的前提下,通过变通的规划模型求解出天然气管网的优化输送方案,算例表明是实用可行的,但对于一般的、影响因素众多的可压缩流优化问题还需继续深入的扩展研究。