考虑多模态贡献的空间网格结构地震损伤评估方法

张玉建 罗永峰† 郭小农 黄青隆

(1.同济大学 土木工程学院，上海 200092；2.中国建筑第八工程局有限公司，上海 200120)

对既有结构定期的检测鉴定和维护，是保障结构安全、正常服役的前提[1-3]，而对结构性能损伤的准确评估，则是进行鉴定和维护的基础。准确描述地震作用下结构的损伤程度与性能退化程度，不仅可以了解结构或构件破坏的模式，也能对震后结构的安全性做出较为准确的评估。关于既有空间结构的地震损伤评估模型，国内外学者已进行了部分研究，目前的研究主要基于结构的特征响应参数进行损伤表征参数的构建，如节点位移、杆件内力、单元应变能[4]、弹塑性耗能[5-6]或组合参数[7-8]等。由于空间结构具有受力形式复杂、非线性效应突出等特点，现有的基于结构特征响应的地震损伤评估方法，通常不具有普适性与统一性，难以直接应用于实际工程，也无法在机理上为空间结构抗震设计与鉴定理论提供依据。为此，部分学者从框架结构静力推覆分析的角度出发，提出基于推覆参数的地震损伤评估方法[9]。然而，由于受到相应的静力推覆分析方法适用对象的限制，此类方法在空间网格地震损伤评估上的适用性还有待验证。

由于结构的整体损伤与结构模态参数具有确定性关系，因此，可通过模态参数的变化构建结构地震损伤的表征参数，进而评估结构的抗震性能退化程度。在研究的早期，学者通常以结构基本模态参数信息的变化[10-11]进行结构抗震性能的评估，如Disasquale等[10]提出采用地震前后基本周期的变化以建立结构整体损伤模型。对于以一阶振型为主振型的框架结构，此类方法评估精度可以得到保证，然而对于受力形式较为复杂的空间结构，由于结构反应受多阶振型影响，其结构性能损伤程度难以用单一模态损伤进行表征[12]。鉴于此，部分学者在构造损伤表征参数时引入了高阶模态参数[13-14]，以考虑高阶模态损伤对结构整体性能退化程度的影响。然而，由于空间结构受力形式的特殊性，其在强震作用下会产生显著的模态跃迁现象，而现有的模态匹配方法在结构产生严重损伤时，匹配效果[15]不甚理想。具体地说，模态跃迁现象会使得结构主振型在损伤前后发生变化，即针对原结构所遴选的主振型与震损结构的主振型并非一一对应。此外，结构在非线性效应较强时所产生的振型耦合效应，也会使得上述方法在适用于线性分析时的模态叠加原理假定条件不再满足[16]，相应的评估结果精度也无法满足实际工程要求。

针对上述问题，本文从模态推覆分析的思路出发，结合动力学理论推导，得到对应于单位地震力作用下考虑多阶模态贡献的等效静力位移表达式，并根据地震前后结构的等效静力位移差异程度，构造结构整体损伤表征参数，进而评估结构地震损伤状态与性能退化程度。最后，根据K6型网壳数值算例分析结果，验证了本文所提方法的有效性与适用性。

1 空间结构多模态整体损伤模型

1.1 考虑多模态贡献的抗震性能评估原理

由结构动力学可知，地震作用下结构任意时刻的位移向量u可表示为

u=qΦ=q1φ1+…+qnφn

(1)

式中：u为结构位移向量；n为模态阶数；Φ={φ1,φ2,…,φn}T为振型矩阵，其中φi为第i阶关于质量矩阵M的正则化振型向量；q={q1,q2,…,qn}为振型坐标向量，其中qi为第i阶振型坐标，其表达式为

(2)

根据模态推覆分析方法的基本思路[16-18]，当忽略非线性效应所引起的振型反应耦合效应时，在反应峰值时刻激发第i阶振型位移向量ui=qiφi所需的等效模态静力荷载Fi为

(3)

(4)

由模态分解原理可知，与此等效静力荷载F相对应的静力位移d为

(5)

由式(4)可以看出，该等效静力荷载包含了结构各阶单位模态荷载，并将其按照振型参与系数进行组合以考虑多阶模态贡献，因此，可将此荷载作为单位地震激励下的等效静力荷载。而在与此荷载相对应的等效静力位移d表达式中，各阶模态位移反应分量包含了模态参数信息ωi、φi和各模态对整体结构反应的贡献程度表征参数γi。因此，可将等效静力位移d作为衡量结构在单位地震力作用下的整体变形能力。

为便于应用，可将等效静力荷载F的表达式进一步化简。

振型参与系数γi表达式为

(6)

式中：R为荷载指示向量。

根据式(6)，并考虑振型的正交性，可得

(7)

化简可得

(8)

因此，式(4)中所列等效静力荷载F也可表示为

(9)

此外，结构位移向量u也可采用分量形式表示为结构6l×1阶的相对位移反应向量，即

(10)

式中，6l为结构自由度数，即6l=n，l为去除结构支座节点的自由节点数目。

此时，根据振型参与系数的定义，式(9)中的荷载指示向量R可表示为

R={ITcosαsinβ,ITsinαsinβ,ITcosβ,0T,0T,0T}T

(11)

式中：I为n×1阶单位向量；α为地震动激励方向与结构坐标X轴正方向的夹角；β为地震动激励方向与结构坐标Z轴正方向的夹角。

因此，在采用特定方向的荷载指示向量R后，由等效静力荷载F所产生的结构位移反应d即包含了沿该方向输入地震动时所激发的模态振型反应，根据该位移反应的大小即可对结构在地震动输入下的变形能力进行评估。

1.2 震损结构损伤评估方法

由1.1节推导可知，根据式(5)、(9)、(11)，结构在地震动输入下的变形能力可通过其在等效静力荷载F作用下的结构位移反应d进行评估。因此，可分别建立原结构与震损结构的等效静力模型，如图1所示。作用在两个结构上的等效静力荷载F可分别分解为多阶单位模态荷载，并按对应模态的振型参与系数进行组合。原结构与震损结构在承受该等效静力荷载作用后的位移反应分别为d与d′，根据位移反应的差异性即可对震损结构抗震性能损伤程度进行评估鉴定。

图1 等效静力模型Fig.1 Equivalent static model

值得说明的是，在传统的基于模态参数的损伤评估方法中，结构当前地震损伤状态的评估是以原结构为基准模型，通过计算各阶模态损伤程度并组合以求得地震损伤表征参数的具体数值。而在本文中，对应于同一等效静力荷载的等效静力位移在推导过程中，均是以结构的当前状态为基准模型。因此，在考虑多模态贡献的基础上，根据等效静力位移的差异程度去评估衡量结构性能退化程度可以避免模态跃迁现象与主振型遴选方式不合理对评估结果准确性的影响。为表征原结构与震损结构在同一等效静力荷载作用下的等效静力位移的差异程度，本文定义位移相关系数(CMD，Correlation of Equi-valent Mode Displacement)RCMD为

(12)

由式(12)可知，位移相关系数RCMD的取值范围为[0,+∞)。当地震作用水平较低时，结构及其内部各构件仍处于弹性工作范围，没有损伤产生，等效静力位移反应d与d′应相等，即RCMD=0。随着地震力作用的增大，结构整体损伤水平逐渐增加。在结构临近倒塌时，震损结构的抗震性能已严重退化，相应的等效静力位移反应d′理论上可趋于无穷大，故此时RCMD=+∞。为便于实际工程应用，结构抗震性能整体损伤评估指标取值范围通常限定在[0,1]之间。因此，需对上述位移相关系数进行区间变换，以满足实际工程应用的要求。此外，由式(12)可知，RCMD数值大小会随着结构自由度数目的增加而不断累积，故在区间变换过程中也需考虑这一影响。综上所述，本文定义结构整体损伤参数D为

(13)

式中，整体损伤参数D的取值范围为[0,1]。

2 数值算例结构模型

2.1 结构有限元模型

为验证本文所提方法的有效性与适用性，本文采用单层球面网壳作为数值算例进行分析，结构布置如图2所示。网壳形式为K6型，跨度为60 m，矢跨比为1/3，环数为10环，屋面荷载为1.5 kN/m2，采用焊接空心球节点，三向铰接支座。结构各杆件所采用的截面规格如表1所示。结构选型和截面设计均满足《钢结构设计标准》(GB50007—2017)和《空间网格结构技术规程》(JGJ7—2010)的要求。

表1 杆件截面信息Table 1 Member section information

图2 单层球面网壳模型Fig.2 Single-layer spherical reticulated shell model

采用有限元软件ANSYSv14.5建立有限元模型。采用梁单元Beam189模拟杆件，所有杆件均为两端刚接，忽略焊接球节点刚域的影响，杆件截面设置16个角栅点。采用质量单元Mass21模拟集中质量，结构集中质量由结构所承受的屋面荷载标准值换算得到。结构分析中计入几何非线性效应和材料非线性效应。钢材密度为7 850 kg/m3，材料本构关系采用理想弹塑性模型，钢材弹性模量为2.06×105MPa，泊松比为0.3，屈服强度为235 MPa。

2.2 地震波选取

本文中选取22条地震波进行分析，其中，2条记录于Ⅰ类场地，10条记录于Ⅱ类场地，8条记录于Ⅲ类场地，2条记录于Ⅳ类场地。原始地震动参数见表2。各地震波阻尼比为0.02，地震动输入方向为x向。采用地震峰值加速度(PGA)aPGA作为地震动输入参数，采用增量动力时程分析方法进行结构地震反应分析计算，以探究结构在强震下变形能力与塑性发展程度的变化过程，并由本文所提方法计算得到结构在不同强度地震动输入下的损伤程度。

表2 地震波信息表Table 2 Seismic excitations information

3 数值计算结果分析

3.1 结构地震损伤演化过程

地震作用下网壳结构产生损伤后，会导致结构刚度和承载力的急剧下降，从而危害结构的正常使用性的安全性。结构在不同程度的地震作用下，随着损伤的逐渐累积，其刚度矩阵、模态振型均产生了不同程度的改变。对于基于模态参数的地震损伤评估方法，如果以原结构的模态参数信息为基准，势必会随着几何非线性与材料非线性的增强而无法保证方法的准确性。表3列出了上述数值模型在不同程度的E1地震波作用下，对应于原结构x向前十阶主振型的模态参数变化。其中，主振型是依据水平x向质量参与系数(MPF)γMPF大于0.01的要求所选取的。可以看出，随着地震动强度的增加，伴随着几何非线性与材料非线性效应的加强，原结构前十阶主振型在震损结构中的振型参与系数γ与质量参与系数γMPF均出现较为明显的变化。特别地，在aPGA=1.0g作用下的震损结构中，原结构前十阶主振型的γ与γMPF均趋于0，这表明相应振型对结构整体地震反应的贡献是可以忽略不计的。因此，在地震损伤评估过程中，如果基于原结构模态参数信息构造整体损伤参数，其评估结果的准确性将无法保证。

表3 原结构主振型在不同损伤程度下的模态参数变化Table 3 Change of modal parameters of original structure with different damage degree

为考虑模态参数信息在损伤演化过程中的时变性，需要根据震损结构的当前模态参数信息进行地震损伤评估。表4给出了结构在不同程度E1地震波(aPGA=0.1g、0.5g、1.0g)作用下，结构的前三阶主振型，以及相应的周期T、质量参与系数γMPF与振型参与系数γ。可以看出，在低损伤程度下(aPGA=0.1g)，震损结构主振型形状及相应的γ、γMPF与原结构较为相近。而在中等损伤程度(aPGA=0.5g)与严重损伤情况下(aPGA=1.0g)，震损结构主振型与原结构已有很大不同。由前述整体损伤表征参数的推导过程可知，本文等效静力模型是依据结构当前模态参数信息所构建的。式(5)所示的等效静力位移表达式中的振型坐标φi、圆频率ω及振型参与系数γ均与震损结构当前状态相对应。然而，与此等效静力位移相对应的等效静力荷载F经推导后可简化为质量矩阵M与荷载指示向量R的乘积，如式(9)所示。因此，在考虑结构当前模态参数信息的基础上，本文所提方法仅需进行等效荷载作用下的静力分析求解而无需进行震损结构的模态分析求解，简化了计算内容，并避免了后续模态信息的提取与组合。

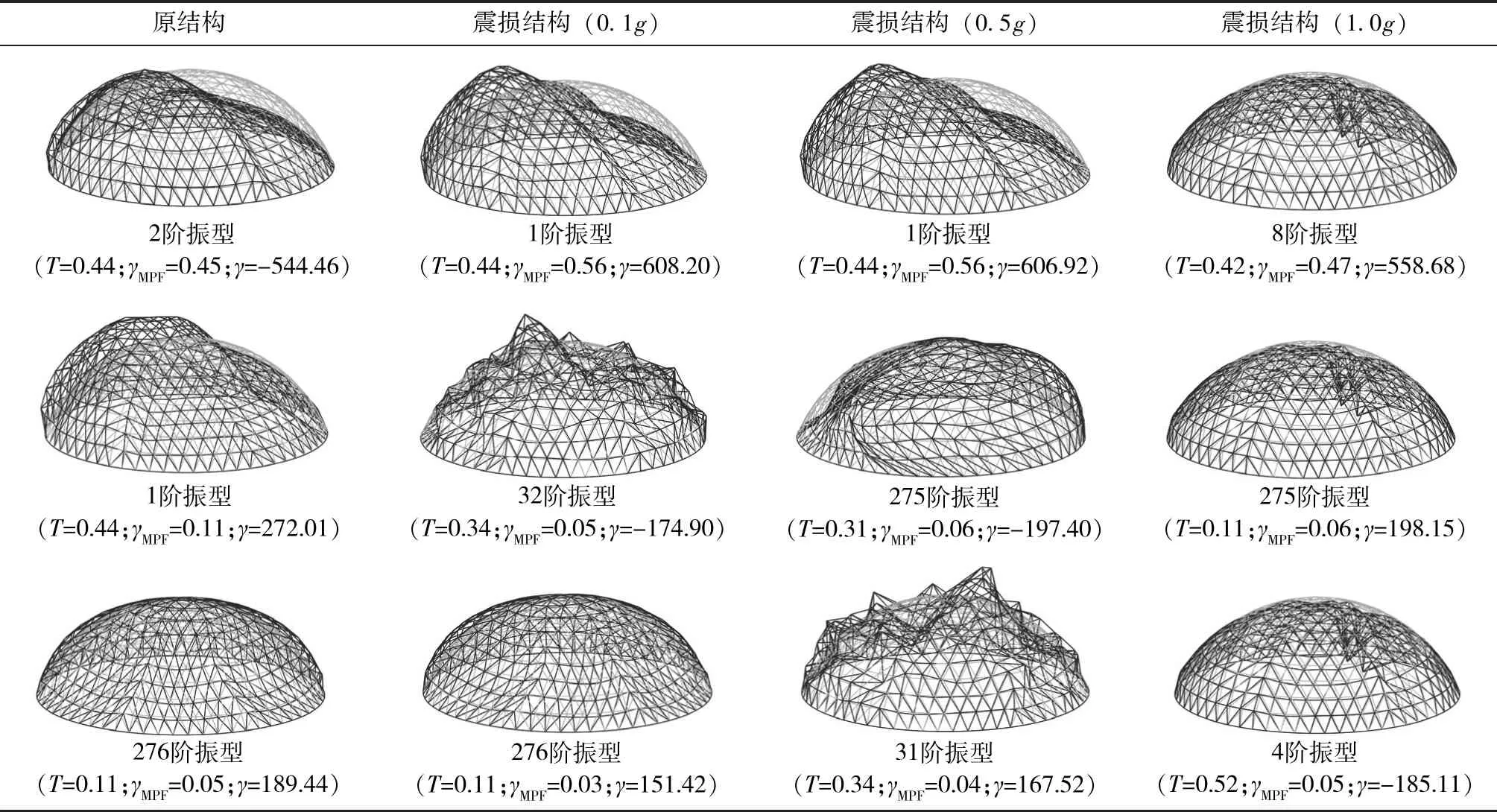
表4 不同损伤程度下的结构前三阶主振型Table 4 First three significant vibration modes of structures with different damage degrees

在同一大小的等效静力荷载F作用下，根据原结构与震损结构的等效静力位移差值，即可由式(12)、(13)计算得到结构整体损伤参数D。图3给出了不同损伤程度下的对应于原结构等效静力位移(Usum)差异程度。可以看出，在地震动激励水平较低的情况下(0.1g、0.3g)，原结构与震损结构的等效静力位移基本相同，由此计算得到的结构整体损伤参数也趋于0。随着地震动输入强度的增加，震损结构的等效静力位移相比原结构已有较大差异，且位移差异较大的区域主要集中在网壳主肋杆处，这表明震损结构等效静力位移表达式中所组合的各阶模态已有不同程度损伤。相应地，由等效静力位移差异程度计算得到的结构整体损伤参数D的增长趋势也与此损伤演化过程保持了较好的一致性，这也验证了本文所提等效静力模型的计算结果的准确性。

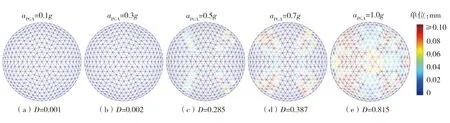
图3 不同损伤程度下的等效静力位移差异程度 (地震波编号:E1)Fig.3 Variation of equivalent static displacement with different damage degrees (Seismic wave number:E1)

3.2 结构整体损伤参数变化曲线

采用选取的地震波对数值算例进行增量动力时程分析，根据数值分析结果研究结构在强震作用下的损伤性能与损伤发展规律，并采用本文所提方法计算得到各地震波激励下的结构整体损伤参数变化曲线，如图4所示。

图4 各地震波作用下的结构整体损伤参数变化曲线Fig.4 Structural overall damage parameter curves under various seismic excitations

现有研究表明，无论是在材料层次，还是构件或结构层次，在不断增大的外部作用下其低周疲劳损伤程度应该总体服从正S型曲线呈现的发展规律，即标准损伤发展曲线[19]，如图5所示。这一曲线由以下5个阶段构成：D0-D1阶段表示结构处于基本完好状态；D1-D2阶段表示结构开始出现损伤，曲线进入第一变速阶段；D2-D3阶段表示结构的损伤演化速率相对恒定；D3-D4阶段表示结构损伤已较为严重，损伤演化速率开始下降，曲线进入第二变速阶段；D4-D5阶段表示结构处于临近倒塌阶段。由图6可以看出，在各地震波不同程度的激励作用下，结构的整体损伤发展曲线较为符合图5所示标准损伤发展曲线所描述的性能退化规律，不同地震波作用下各损伤阶段所对应的损伤参数范围也具有较好的一致性。

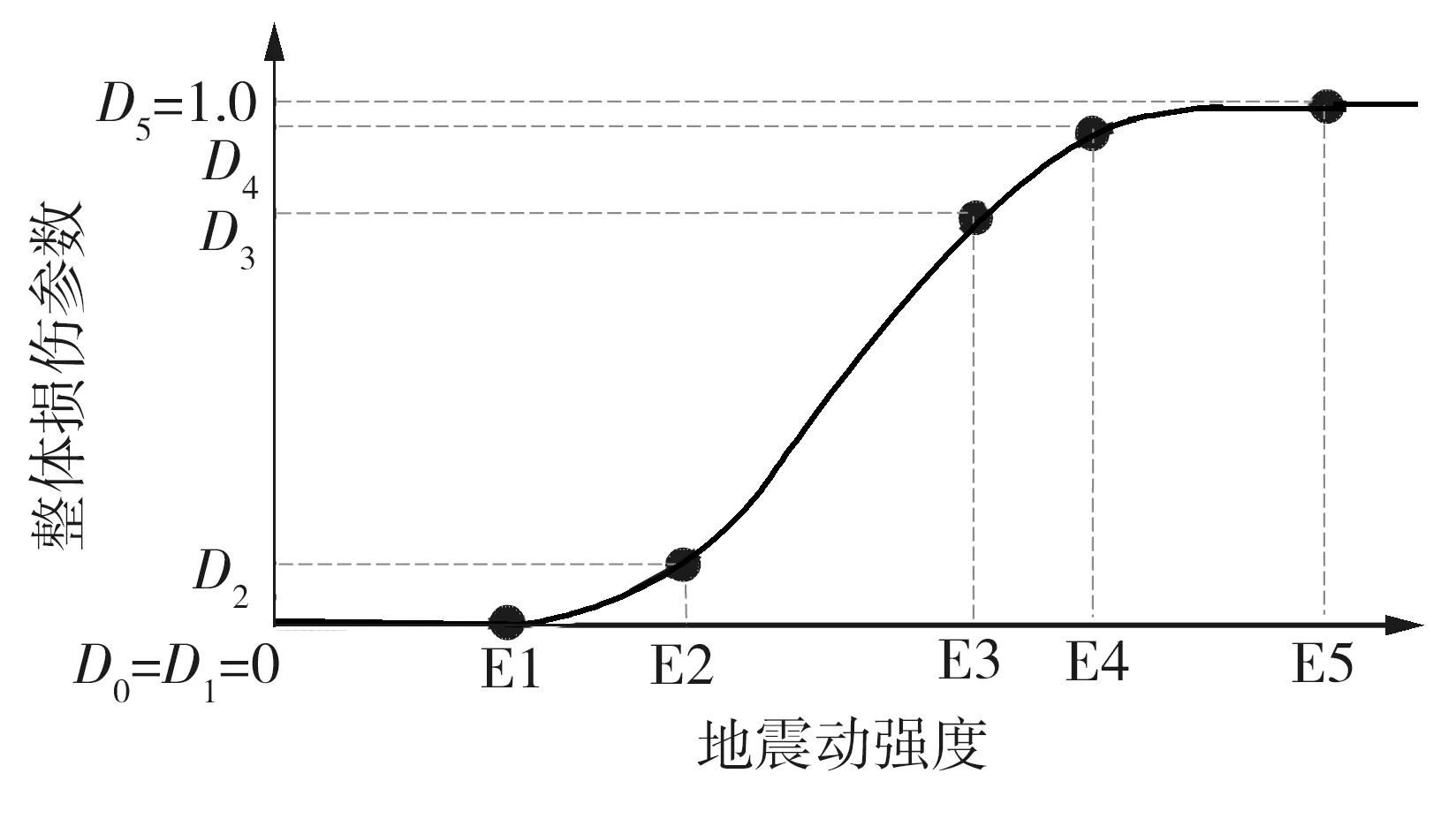
图5 标准损伤发展曲线Fig.5 Standard damage development curve

为便于比较，可将图4所示各地震波作用下的结构整体损伤参数变化曲线进行不同比例缩放，即将损伤参数D=1.0时所对应地震峰值加速度对应至比例因子为1的情况，并计算各地震波作用下结构整体损伤比例发展曲线的平均值与95%保证率下的置信区间，如图6所示。

图6 结构整体损伤比例发展曲线Fig.6 Proportional development curve of overall structural damage

由图6可以看出，各地震波作用下的整体损伤比例发展曲线平均值与95%置信区间上下限曲线同图5所示的标准损伤发展曲线相比均具有较好的一致性。事实上，D1-D2阶段(比例因子为0.3～0.5)，即第一变速阶段的出现，是因结构进入塑性发展阶段所导致的，伴随着塑性发展的逐渐深入，结构的损伤演化速率相对恒定，曲线进入相对稳定的D2-D3阶段(比例因子为0.5～0.7)。而D3-D4阶段(比例因子为0.7～0.9)，即第二变速阶段的出现，则标志着结构因几何非线性效应加深而进入刚度快速退化阶段。上述分析可在3.3节的方法有效性验证中得到证明。在不同地震波作用下，结构在严重损伤情况下的位移响应与塑性发展深度有所不同，这是由地震动卓越频率与结构主振型共振区是否接近所决定的[20]。因此，如图6所示，当比例因子位于0.7～0.9区段时，其对应的95%置信区间上下限包围区域存在明显扩大的现象。上述结构损伤发展曲线的变化规律及损伤发展阶段划分也可与我国《建(构)筑物地震破坏等级划分》(GB/T 24335—2009)规范中的五阶段性能水准划分原则相对应，其各阶段的性能水准临界点，可由各类空间网格结构在不同地震波作用下的增量动力时程分析结果及相应的结构整体损伤参数确定。限于篇幅，本文不再赘述。

3.3 方法有效性验证

为验证本文中所提方法的有效性，仅根据结构整体损伤参数曲线的变化规律去定性分析显然是不充分的，仍需将结构整体损伤参数变化曲线即损伤发展曲线与结构整体特征响应曲线进行对比论证。

本节选取4种结构特征响应作为方法的对比参数，分别为节点最大竖向位移(Uz)、节点最大三向合位移(Usum)、塑性杆件比例(Rym)、杆件平均塑性发展程度(Pave)。其中，节点最大竖向位移与节点最大三向合位移均对应于震后时刻；塑性杆件比例为经历地震后结构进入塑性的杆件数目占总杆件数目的比例；杆件平均塑性发展程度是在统计各杆件单元进入塑性的积分点数目占总积分点数目的比例后取平均值，用以反映各杆件单元的塑性发展深度。限于篇幅，本节仅选取两条地震波所对应的损伤发展曲线与特征响应曲线进行对比，如图7、图8所示，相应的地震波编号分别为E1与E21。

图7 结构整体损伤参数变化曲线与特征响应变化曲线对比(地震波编号:E1)Fig.7 Comparison between structural overall damage parameter curves and structural characteristic response curves (Seismic wave number:E1)

由图7(a)、7(b)可以看出，当E1的地震峰值加速度aPGA=0.3g～0.8g时，结构整体损伤参数变化曲线在结构进入塑性阶段后出现第一次快速增长。伴随着材料非线性效应的逐渐加强，结构整体损伤程度呈现匀速增长趋势，此时，结构的位移响应仍处于较低水平(Uz与Usum均小于0.15 m);而当aPGA=0.8g～1.1g时，损伤发展曲线出现第二次快速增长，这对应着结构因几何非线性效应加深所产生的刚度快速退化阶段。随着结构位移响应的快速增长，损伤程度的增长速率出现进一步增大直至结构倒塌。由图8(a)、8(b)可以看出，在E21地震波作用下，结构整体损伤参数变化曲线的变化也具有上述规律，即当aPGA=0.2g～0.5g时，伴随着杆件材料进入弹塑性阶段，曲线出现第1次快速增长；当aPGA=0.5g～0.6g时，因结构刚度快速退化，曲线出现第二次快速增长。值得注意的是，在E1地震波作用下，结构失效前的位移响应较大，杆件塑性发展已相当深入，呈现动力强度失效的特征[20-21]，其整体损伤参数的增长速率也较为均匀。而在E21地震波作用下，结构失效前的位移响应存在突变现象，塑性杆件比例与塑性发展程度均低于E1地震波作用的情况，呈现偏于动力稳定失效的特征。由图8可以看出，与此类失效模式相对应，结构的整体损伤参数曲线的变化趋势也具有类似的特征，即当PGA位于0.5g附近时，整体损伤参数由0.6附近很快突增至1，这也从侧面验证了本文所提方法的有效性。综上所述，整体损伤参数的总体变化趋势与结构特征响应密切相关，可将其作为表征空间网格结构地震损伤状态的指标参数。

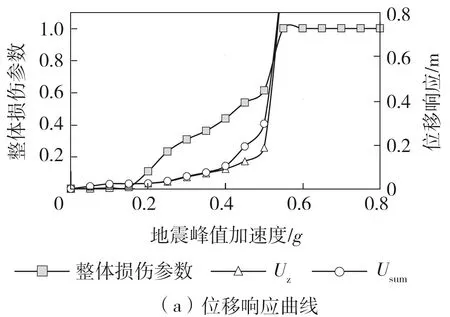
图8 结构整体损伤参数变化曲线与特征响应变化曲线对比(地震波编号:E21)Fig.8 Comparison between structural overall damage parameter curves and structural characteristic response curves (Seismic wave number:E21)

3.4 方法对比

为验证本文所提方法的合理性，对数值算例进行增量动力时程分析，分别采用本文方法、DE模型损伤评估方法[10]、SHI模型损伤评估方法[13]、HE模型损伤评估方法[12]计算得到各自的结构整体损伤参数变化曲线并进行方法对比验证，结果如图9所示。

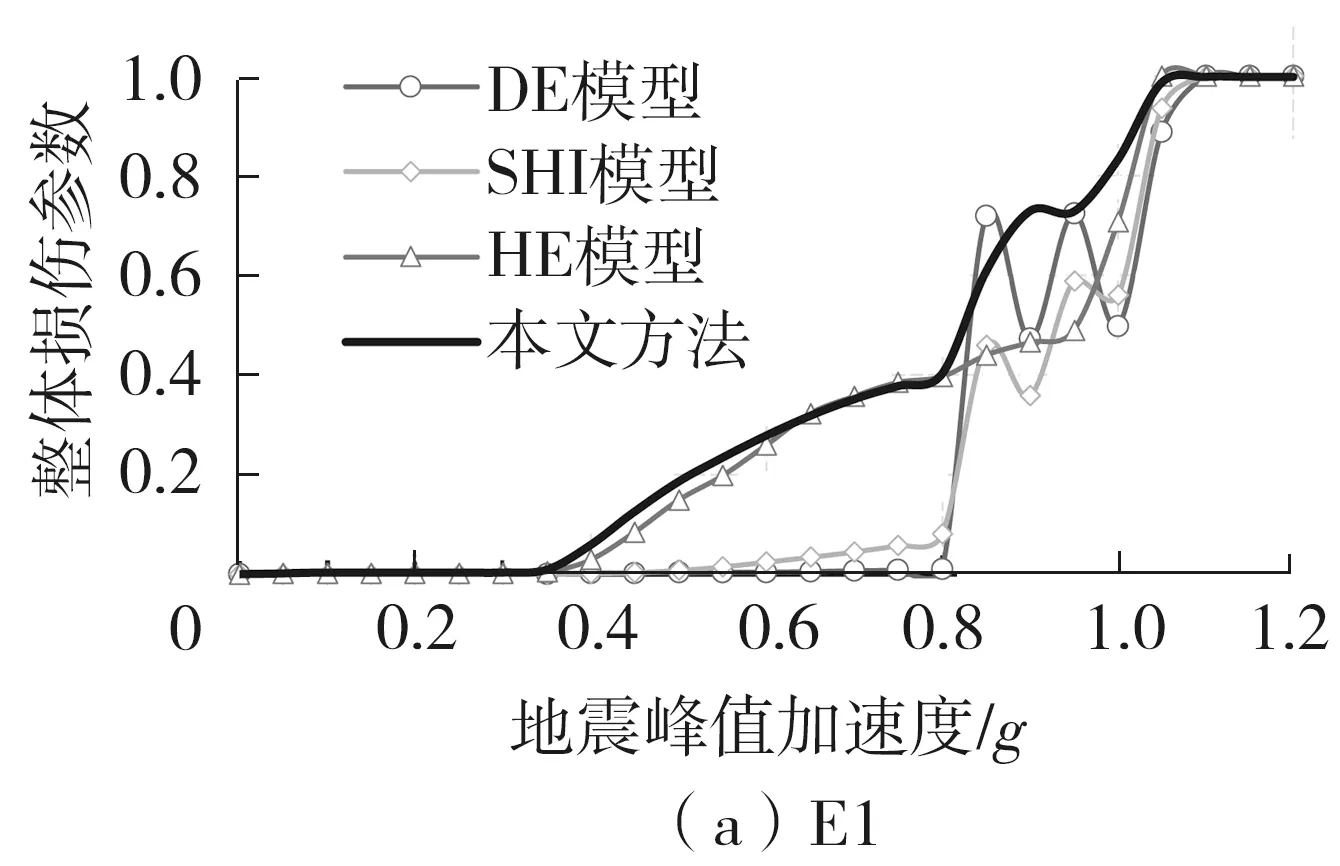
图9 各类方法的结构整体损伤参数变化曲线对比Fig.9 Comparison of structural overall damage parameter curves generated by various methods

由图9可以看出，在结构塑性发展已较为深入时，按照仅考虑基本模态的DE模型损伤评估方法与粗略考虑高阶模态影响的SHI模型损伤评估方法的计算得到的损伤参数仍趋于0，对结构抗震性能损伤程度的评估过于保守，且损伤发展曲线具有很强的震荡性。而考虑多阶模态组合的HE模型损伤评估方法在损伤程度较低阶段与本文所提方法的计算结果基本相同，但在结构进入严重损伤阶段甚至临近倒塌时，仍具有一定的差异性。如图9(a)所示，当aPGA=0.8g～1g时，采用本文所提方法计算得到的损伤参数稍大于HE模型损伤评估方法的计算结果。产生这一差异现象的原因可归结为以下两点：其一是结构在不同损伤程度下主振型的变化，使得针对原结构所遴选的主要振型不再是震损结构的主振型，这一结论可根据第3.1节中的计算结果得到证明。这使得结构在严重损伤状态下计算得到的损伤程度会由于震损结构的主振型损伤信息被遗漏而偏小；其二是在严重损伤情况下存在的振型耦合问题，使得采用现有的模态匹配方法难以对原结构的振型进行准确匹配。例如，HE模型损伤评估方法中采用线性模态置信准则(LMAC)比较地震作用前后模态振型向量的相似度，以达到寻找模态匹配关系的目的。以E1地震波作用下原结构第3阶、18阶、33阶模态振型为例，图10给出了上述模态在不同程度地震动激励下采用LMAC法计算所得模态匹配系数。如图所示，原结构模态在结构产生损伤后出现了明显的模态跃迁现象，例如原结构第3阶模态与震损结构(aPGA=1.0g)的第29阶的模态匹配系数最大。然而，在严重损伤情况下，原结构相应振型与震损结构各振型匹配系数的差异性并不明显，例如震损结构在aPGA=0.1g时与原结构第3阶模态的最大匹配系数为1.0，而在aPGA=1.0g时的最大匹配系数仅为0.22，此时的模态匹配系数次大值为0.21。可以看出，结构在严重损伤情况下的模态匹配程度是相近且不易区分的。

图10 基于LMAC准则的模态振型匹配结果Fig.10 Modal matching results generated by the LMAC criteria

由于现有损伤评估方法难以对原结构的振型进行准确匹配，相应评估结果的准确性也会随之降低。随着结构非线性效应的加强，上述因素对结构性能损伤评估的影响将不可忽视。根据第1.1、1.2节理论推导过程可知，由于本文所提方法在构建损伤表征参数时已包含了结构的各阶振型信息，且构造过程中不依赖于原结构的模态参数，因此避免了上述问题的产生。由图8(b)可以看出，由于在E21地震波激励作用下结构呈现动力稳定失效的特征，其在临近倒塌前的节点位移与杆件塑性发展程度并不突出。因此，在严重损伤情况下，与之相应的结构主振型变化与振型耦合对评估结果的影响可忽略不计。此时，依照本文所提方法与HE模型损伤评估方法计算得到的结构整体损伤参数较为相近。

4 结论

本文从模态推覆分析的思路出发，结合动力学理论推导，得到对应于单位地震力作用下考虑多阶模态贡献的等效静力位移表达式，并根据地震前后结构的等效静力位移差异程度，构造结构地震损伤表征参数，即结构整体损伤参数，进而评估结构地震损伤状态与性能退化程度。数值算例分析结果表明，根据本文方法计算得到的结构整体损伤参数在考虑多阶模态贡献的基础上，可较为准确地评估大跨度空间网格结构地震损伤程度，具体结论如下：

1)本文提出的空间网格结构地震损伤评估方法考虑了结构多模态损伤贡献，同时由于公式推导过程中均以结构当前状态为基准，避免了模态跃迁现象与主振型遴选方式不合理对评估结果准确性的影响；

2)算例结果表明，在不同程度地震波的激励作用下，依据本文方法计算得到的结构整体损伤参数变化曲线与标准损伤曲线、结构特征响应曲线对比均具有较好的一致性，从而验证了本文所提方法在空间网格结构地震损伤评估中的有效性与适用性；

3)通过对比其他地震损伤评估方法计算结果，证明了地震损伤评估方法中考虑多阶模态贡献的必要性，同时也验证了当结构发生严重损伤情况时，本文所提方法在考虑多阶模态贡献的基础上可避免因振型耦合效应、主振型遴选方式不合理等因素对损伤评估结果准确性的不利影响。