余倾斜挠类和包络余模

2021-12-07姚海楼

北京工业大学学报 2021年12期

李园，姚海楼

(北京工业大学理学部，北京 100124)

倾斜理论在代数表示论中有着举足轻重的作用. Brenner等[1]于20世纪80年代建立了倾斜理论，Angeleri-Hügel等[2]研究了包络理论与倾斜理论之间的关系. 用代数表示论的方法来研究余代数，是近些年来的热点问题. 本文主要引入了关于余代数的余模(预)包络以及极大余倾斜余模和包络余模等概念，证明了在余代数中当余倾斜挠类是包络类时，它是由包络余模唯一表示的. 余代数的表示理论也取得了很大的成就[3-15]. Lin[16]讨论了3种不同类型的余代数，即co-Frobenius余代数、半完备余代数和有理余代数. Năstăsescu等[17]定义了遗传余代数并研究了它的基本性质. Wang[18]引进了余代数上的倾斜余模和偏倾斜余模的概念，并得到了它的一些基本结果. Simson[19]研究了余倾斜余模，并且在箭图余代数中给出了不同的有趣的例子. 另外，Simson研究了Hom-可计算余代数、Euler余代数[20]，以及驯顺余模型余代数[21]. Liu等[22]给出了n-自余倾斜余模和n-余倾斜余模的定义，并得到了n-自余倾斜余模和n-余倾斜余模可以诱导余模之间的等价.

受文献[2]的启发，在余代数上将把包络理论与余倾斜理论建立联系. 在本文，对于一个余代数，引入了余模的(预)包络以及极大余倾斜余模和包络余模的概念，并得到了在余代数中当余倾斜挠类是包络类时，它是由包络余模唯一表示的.

1 预备知识

令C是一个余代数，C-Comod表示左C余模范畴.如果没有特殊说明，本文中的余模都是指左C余模.用HomC(X,Y)表示余模X、Y之间的映射.用Gen(T)表示若干个T的直和的满同态像，也就是说，对任意的M∈GenT，都存在一个基数I使得ψ:T(I)→M是满射.令M∈C-Comod是一个余模类，记Add(M)为M中元素的直和的直和项所构成的余模类.对应地，记add(M)为M中元素的有限直和的直和项所构成的余模类.类似地，记Prod(M)为M中元素的直积的直和项所构成的余模类.如果M={M}，则分别写成AddM、addM.对所有的M∈M，记

如果C是一个半完备余代数，那么它就有足够多的投射对象.

下面给出预包络的定义，并研究它们的性质.

定义1令ξ⊆C-Comod是一个余模类且M∈C-Comod.如果φ∈HomC(M,X)，其中X∈ξ，且对每个F∈ξ，HomC(φ,F):HomC(X,F)→HomC(M,F)都是满态射，则称φ是M的ξ-预包络.

注1令φ∈HomC(M,X)是M的一个ξ-预包络.

1) 若gφ=φ且g∈End(X)，则有g是X的一个自同构，称φ是M的ξ-包络.

2) 若φ∈HomC(M,X)是满态射且Cokerf∈⊥ξ，则称φ是特殊的ξ-预包络.

如果每一个余模都有一个ξ-(预)包络，则称ξ⊆C-Comod是一个(预)包络类.

引理1令φ1:M→F1和φ2:M→F2是M的2个不同的ξ-包络，则F1≅F2.

证明：取M的2个不同的ξ-包络，φ1:M→F1和φ2:M→F2，则有2个余模映射f1:F2→F1和f2:F1→F2，满足交换图，如图1、2所示.

图1 φ1的交换图Fig.1 Commutative diagram of φ1

图2 φ2的交换图Fig.2 Commutative diagram of φ2

于是，φ2=f2φ1和φ1=f1φ2.由此可得φ2=f2f1φ2和φ1=f1f2φ1.由φ1和φ2都是M的ξ-包络可知，f2f1和f1f2都是自同构.因而，f1和f2既是单态射又是满态射，即它们都是同构的.因此，F1≅F2.

引理2如果M有一个ξ-包络和φ:M→F是一个ξ-预包络，则存在F的子余模F′和K使得F=F′⊕K，并且合成π∘φ:M→F′是M的一个ξ-包络，其中π是F到F′的投影.

证明：取M的一个ξ-包络θ:M→F0，则有交换图，如图3所示.

图3 M的交换图Fig.3 Commutative diagram of M

故φ=fθ和θ=gφ，由此可得θ=gfθ.由假设可知，gf是F0的自同构.并且，有F=Imf⊕Kerg.因此，F′=Imf≅F0并且M→F′是M的一个ξ-包络.

引理3设M有一个ξ-包络.令φ:M→F是M的ξ-预包络，则φ是ξ-包络的充分必要条件是不存在直和分解F=F′⊕K，并且K≠0和Imφ⊂F′.

证明：⟹假设φ:M→F是一个ξ-包络.取一个分解F=F′⊕K，并且K≠0和Imφ⊂F′.令f′:F′⊕K→F′是F到F′的投影态射.令η:F′→F=F′⊕K是典型的单态射，则有余模映射f=ηf′:F′⊕K→F.容易验证φ=fφ.因φ:M→F是一个ξ-包络，故f是一个自同构.于是，K=0，这与假设矛盾.

⟸由引理1和引理2可得.

图4 直和的交换图Fig.4 Commutative diagram of the direct sum

定理1对于余模类ξ⊆C-Comod，令W是投射生成子，φ:W→B是W的ξ-预包络，则HomC(W,B)是一个循环EndB模且Prodξ⊆GenB.

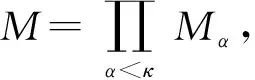
图5 φ(I)的交换图Fig.5 Commutative diagram of φ(I)

图6 直积的交换图Fig.6 Commutative diagram of the direct product

2 finendo和预包络

介绍了finendo余模的定义，并研究了预包络与finendo余模之间的关系.

定义21) 令W是投射生成子,如果存在一个γ和余模映射f:W→B(γ)使得对每个α,所有的余模映射W→B(α)都可以通过f进行分解，其中γ和α是基数，则余模B称为W-finendo.

2) 如果余模B是W-finendo，其中W是投射生成子，则称B是finendo余模.

命题1设C是余代数，W是投射生成子，且T∈C-Comod，则下面的2个条件是等价的:

1)T是finendo余模；

2) 存在一个基数β使得对任意的α，所有的余模映射W→T(α)都可以通过若干个T(β)的直积进行分解.

证明：1)⟹2)因为T是finendo余模，则存在一个基数β使得对每个基数α,余模映射φ:W→T(α)都可以通过h:W→T(β)进行分解.令I=HomC(W,T(β)),取T(β)的第h个投影映射η:[T(β)]I→T(β)，并且令g:W→[T(β)]I是I中所有的映射诱导的对角映射，则有交换图，如图7所示.因此，φ=fηg，进而得到2).

图7 finendo余模T的交换图Fig.7 Commutative diagram of finendo comodule T

图8 φ的交换图 Fig.8 Commutative diagram of φ

命题2设C是余代数，W是有限维的投射生成子,则对于一个余模T,下面的3个条件是等价的：

1)T是finendo余模.

2)W有一个addT-预包络.

3) GenT是一个预包络类.

证明：1)⟹2)对一个映射φ:W→X,其中X∈addT,则存在基数α及满态射π:T(α)→X.因为W是投射的,所以有一个余模映射g:W→T(α)使得πg=φ.因为T是finendo余模，所以对于任意一个基数α和g:W→T(α),存在一个基数γ和f:W→T(γ)使得g可以通过f进行分解.因此,有交换图，如图9所示.

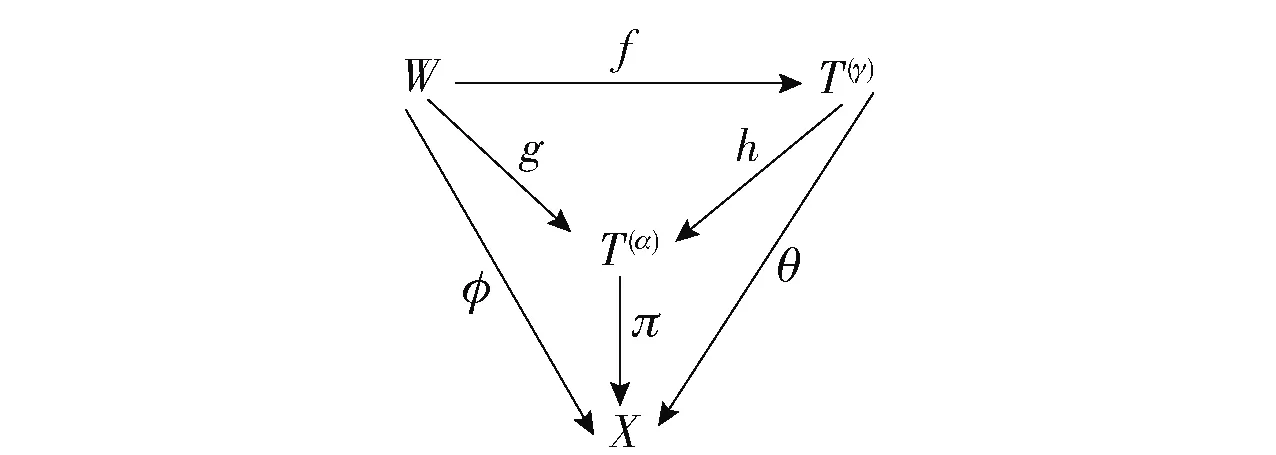
图9 f的交换图 Fig.9 Commutative diagram of f

于是有πhf=φ.因此,令θ=πh并立即得到f:W→T(γ)是addT-预包络.

2)⟹3)取一个addT-预包络ψ:W→B.首先,想证明ψ也是GenT-预包络.假设f:W→X是任意的余模映射，其中X∈GenT.则对于某个J有一个满态射ρ:T(J)→X.由W的投射性，可知f=ρf′，其中f′:W→T(J).取有限子集J0⊆J,即i:T(J0)→T(J)是单态射.然后取f″:W→T(J0)使得if″=f′.因为ψ:W→B是一个addT-预包络，所以有一个g:B→T(J0)使得f″=gψ.因此，有交换图，如图10所示.

图10 ψ的交换图Fig.10 Commutative diagram of ψ

所以igψ=f′,并且ρigψ=ρf′=f.因此,ψ也是GenT-预包络.取任意的A⊆C-Comod，因为W是一个投射生成子，则存在一个满态射π:W(I)→A.于是有推出图，如图11所示.

图11 推出交换图Fig.11 Commutative diagram of pushout

因π是满态射，可知σ也是一个满态射，并且有B′∈GenT.由引理4可知，ψ(I)是一个GenT-预包络.因此,对于f:A→X，其中X∈GenT,存在一个θ:B(I)→X使得fπ=θψ(I).由推出的性质可知，有唯一的α:B′→X使得f=αb′.因此，b′是一个GenT-预包络.又因为A是任意一个余模，故GenT是一个预包络类.

3)⟹1)令ψ:W→X是一个GenT-预包络，其中X∈GenT.则 HomC(ψ,T(α)):HomC(X,T(α))→ HomC(W,Tα)是满态射.因此,对于任意g:W→T(α),有一个h:X→T(α)使得g可以通过ψ进行分解.因为X∈GenT,所以有满态射π:T(γ)→X，其中γ是基数.因为W是一个投射生成子,所以有一个f:W→T(γ)使得ψ=πf.故hπf=g.因此，T是finendo余模.

3 主要结果

首先给出极大余倾斜余模和包络余模的定义，然后研究余倾斜挠类和极大余倾斜余模之间的关系，最后进一步地研究当余倾斜挠类是包络类时，它与包络余模的关系.

定义3如果余模T满足下面的3个条件，则称T是余倾斜余模:

1) proj.dim(T)≤1.

3) 存在一个正合列0→W→T1→T2→0，其中W是投射生成子，Ti∈AddT.

注21) 如果一个余模T满足定义3中的1)和2)，则称T为偏余倾斜余模.

2) 如果对于一个余倾斜余模M∈C-Comod，有ξ=Gen(M)，则称ξ是一个余倾斜挠类.

令C是一个余代数，M∈C-Comod.用spn(M)表示生成余模M的C-子集的最小基数.令ξ⊆C-Comod是余倾斜挠类.用trank(ξ)表示spn(T)的最小值，其中T为历遍所有使得ξ=Gen(T)的余倾斜余模.

1) 对每一个α<κ，Tα是一个余倾斜余模.

2) 对每一个α≠γ<κ，Tα不同构于Tγ且Gen(Tα)=Gen(Tγ).

3) 对每一个α<κ，spn(Tα)=trank(GenT).

4) 如果T0是使得GenT0=GenT和spnT0=trank(GenT)成立的余倾斜余模，则存在一个α<κ使得T0≅Tα.

注3由定义4可知，每个极大的余倾斜余模是余倾斜的.

为了更好地刻画余倾斜余模类，在极大余倾斜余模和余倾斜挠类之间建立一个双射.

设C是一个余代数，用L表示所有在C-Comod中的余倾斜挠类的集合.

定理2设C是一个余代数，用P表示所有在同构意义下的极大余倾斜余模的集合，则P和L之间存在一个双射.

当余倾斜挠类T是包络类时，有下面的结果.

定义5令C是一个余代数，定义

U={T∈L|T是一个包络类}

另外，如果存在子余模T0⊆T满足下面的3个条件：

1)T0≅W，其中W是投射生成子.

3) 不存在包含T0的T的真直和项.

则称T∈C-Comod为包络余模.

定理3令C是半完备余代数.用W表示在同构意义下的所有的包络余模类，则从U到W存在一个单射.

证明：定义φ:U→W：φ(T)=P其中W→P是W的ε-包络.先证明φ是定义良好的.令ε∈U，取正合列

其中θ:W→T是W的ε-包络，且θ是单射，因为ε包含所有的内射余模.因此，W≅T′，其中T′⊆T，即定义5中的1)是成立的.由引理3可知定义5中的3)是成立的.由定理1可知，Prod(ε)⊆Gen(T)，又由T∈ε可知Gen(T)⊆ε.因此，ε=Gen(T).又因为ε是一个包络类，则有ε=Gen(T)=Gen(T⊕T0)=(T⊕T0)⊥⊆T⊥.