(五年级)如何利用连方求和加强计算的思考性
2021-12-06吕琼华
吕琼华
加强计算的思考性,对于发展学生的运算能力至关重要。借助对数表中三连方求和的计算,可以有效促进学生运算能力的提高和思维的发展。
一、初次探究明关系
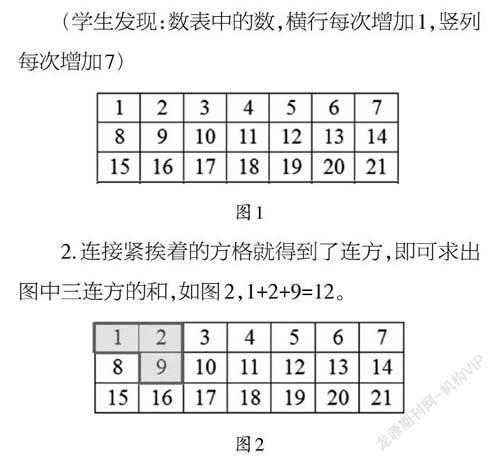
1.下面的数表(如图1)有什么特征?
(学生发现:数表中的数,横行每次增加1,竖列每次增加7)
2.连接紧挨着的方格就得到了连方,即可求出图中三连方的和,如图2,1+2+9=12。
3.把图2中三连方所在位置称为“起始位置”,将三连方往右平移3格,即可求出“终止位置”三连方的和。
(1)方法交流。
方法1:终止位置三连方中的数为4、5、12,和为4+5+12=21。
方法2:12+3×3=21。三连方向右平移3格,每个数都增加3,和一共增加了9。
(2)比较归纳。
哪种方法更快,可以怎样算?(终止和=起始和+右移格数×3)
二、再次探究理思路
1.若数表按规律往下继续展开,求起始位置三连方往下平移5格后的连方之和。
2.方法交流。
方法1:起始位置的三连方中最小数为1,1下移5格后得到36,则终止位置三连方中的最小数为36,写出36右边的数为36+1=37,37下面的数为37+7=44,三连方之和为36+37+44=117。
方法2:每往下平移1格,连方中每个数增加7,下移5格则增加5×7=35。由此可得终止位置三连方中的三个数是:1+35=36,2+35=37,9+35=44,三连方之和为36+37+44=117。
方法3:向下平移5格,连方中的每个数都增加7×5=35,一共增加35×3=105,因此三连方之和为12+7×5×3=117。
3.用以上哪种方法可以解决“三连方从起始位置往下平移n格,求和”的问题?
4.归纳:起始位置和是12,平移后连方中每个数都增加7n,一共增加3个7n,即21n。可以得到:终止和=起始和+下移格数×21。
三、三次探究建模型
1.提出问题:向两个方向平移后,连方和会怎样变化?
2.自主探究。
(1)起始位置三连方向右平移____格,再向下平移____格,求终止位置三连方之和。(在横线上填数后自主研究)
(2)起始位置三连方向右平移n格,再向下平移m格,求终止位置三连方之和。
3.交流(略)。
4.总结:终止和=起始和+右移格数×3+下移格数×21。
本节课以连方求和为载体,引导学生在三次探究過程中逐层进阶,明晰数表关系。同时借助形的位置变化探究数的变化规律,在数形结合中提高学生的计算技能和逻辑推理能力,促进学生的数学思考。
(浙江省杭州市上城区教育学院 310002)