中国农业资源效率时空分异与驱动因素研究

刘玉杰，耿献辉

（1.天津外国语大学 国际商学院，天津 300270；2.南京农业大学 经济管理学院，江苏 南京 210095）

进入新时代，我国政府将全面乡村振兴和城乡融合发展上升为国家重要发展战略，农村优先发展已成为显著趋势[1]。农村要想振兴和发展，必然要保障农业的长期健康发展。可是近年来我国农业自然资源损害严重，化肥、农药、地膜等农业生产要素的不当使用又使得农业环境深受污染，对粮食生产安全和农业绿色发展造成了较大隐患[2-3]。在此背景下，农业资源使用效率的提高成为了推动农业长期健康发展的破局之法，即通过要素资源的科学高效配置使农业生产获得更大产出。不过在现有的研究中，农业资源效率的定义并未有明确的界定，学者更多关注的是农业中具体资源要素的效率，基于此，可借鉴相关学者对于农业具体资源的定义，将农业资源效率描述为在产出和其他投入要素不变的情况下，决策单元最优资源使用数量与实际使用资源数量的比值。而在实际测度中，则是判定在农业生产过程中农业资源的消耗在农业产出中所占比值的大小[4-6]。

对农业资源效率进行研究，首先面对的问题是对其进行测度。在对象上，我国学界关于农业资源效率与生产效率的研究已颇多，主要侧重在各种农业要素的使用效率及其带来的农业生产效率水平的变化。其中最为重要的便是土地、水资源以及农药化肥的使用。在土地方面，梁流涛对我国农业用地的效率水平进行了评价分析和时空上的描述[7]。张合林等探讨分析了城乡融合发展与土地资源利用效率之间的关系[8]。同时基于我国土地使用状况与制度的改变，也会对农业生产效率产生显著的影响[9-10]。农业发展离不开对水资源的利用，现有研究也探索分析了中国农业水资源的利用效率情况及其在区域上的异质性[11-12]。在农药化肥方面，王建华等对农药的转化效率进行了考察[13]，展进涛等对果农施用农药的效率进行了测度[14]。在方法上，学者根据自己的研究内容各有选择，包括如混合距离函数模型[15]，比值分析法[16]，DEA方法[17-19]，面板随机前沿等方法[20-21]，整体上以选取DEA为代表的非参数测算方法居多。

既有研究分析了农业生产过程中具体层面的资源利用效率以及生产效率问题，为我国农业资源的最优配置与利用献计献策。但是就整体性的农业资源效率分析而言还涉及较少，也鲜有对其进行时空分布特征的描述和驱动因素的研究，而这些内容又对于农业绿色和高效发展有着十分重要的意义。正是在这样的背景下，本研究从对农业资源效率进行测度这一问题出发，着重探索我国农业资源效率的时空分布特征与驱动因素，并基于水平测度，进行更深层次的研究。本研究在已有研究的基础上采用面板随机前沿模型（SFA）对中国农业资源效率水平进行评估。之所以选用此模型而不采用DEA方法，主要是基于如下两点的考虑，一是DEA方法对面板数据的兼容性不够，本研究所使用的是2007—2018年的全国30个省市区的面板数据，若使用DEA方法对截面数据进行分开处理，难免有失数据的整体性分析和对比。二是相比于DEA方法，SFA作为参数估计方法能够进行参数的估计检验，由此可更进一步地优化模型并判定估计参数的显著性水平。因而相比于DEA方法，SFA与本研究的数据和分析思想更为适配，故最终选取SFA模型。在此基础上，采用核密度函数分析农业资源效率总体演变特征，最后运用空间面板回归模型探究影响农业资源效率的主要驱动因素。借以通过完整的实证分析为我国的农业资源配置和长期健康发展提供相应的决策支持和实践参考。

一、研究方法与指标构建

（一）研究方法

1.面板随机前沿（SFA）模型

SFA分析方法最早由Aigner 等和 Meesuen等提出[22-23]，经后续逐步拓展，已能够较好用于面板数据的效率分析。SFA适用于做一个产出，多样投入的模型，其基本设定如下。

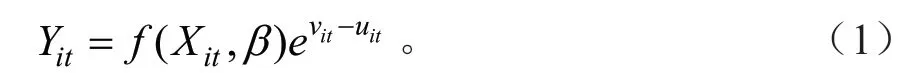
式中：Yit代表省份i在第t年的农业产出，Xit代表省份i在第t年的农业资源投入，f(·)为生产前沿函数。vit表示不可观测的随机扰动项，假设服从期望为0，方差为的正态分布。uit表示农业实际产出与前沿水平的距离，即无效率误差项，假设服从期望为μ，方差为的非负半正态分布。假定与是相互独立的。式（1）反映了农业资源效率不随时间变化的情形，但是本研究的研究年限达12年之久，且中国的农业水平在近年来发展迅速，因而对uit作出如下的假定。

式中：η表示时间因素对uit的影响，η＞0表示uit随时间推移递减，η=0表示uit不随时间发生变化，η＜0表示uit随时间推移递增。由此则将效率时不变模型拓展为时变模型。那么各个省份的农业资源效率即为该省份实际农业产出期望与随机前沿期望的比值（式3）。

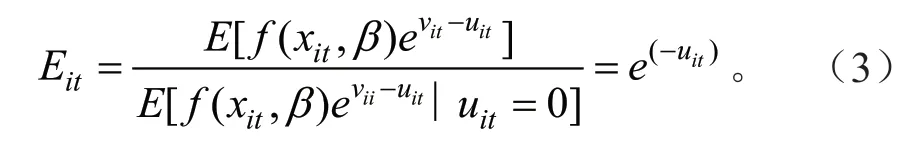
以上分析了随机前沿分析下效率水平的测算，但是其前提为需要假设无效率项uit的存在，对于这一前提需要运用Battese提出的γ判别法进行判定（式4）。

式中：γ表示的是无效影响因素对个体效率差异的解释程度。若γ接近于1，表明误差主要来源于生产技术的无效率，适用SFA模型，若γ接近于0，则不适用SFA模型。

基于如上分析，本研究选用基准的柯布-道格拉斯函数形式的建模方程，构建如式（5）的SFA模型。

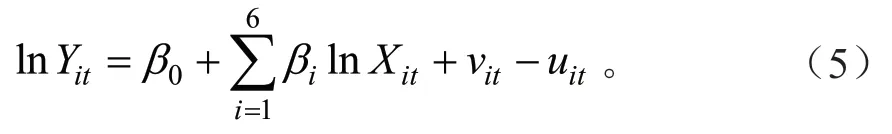
式中：Y代表农业产出；Xi（i=1...6）分别代表下文6种投入要素；i代表省份，t代表年份。

2.核密度函数分析

核密度估计方法作为一种非参数估计方法，可以避免函数形式预设而引起的实际值与测算值之间的差异，能更直观的反映客观事实。通过波峰形状和数量可以对农业资源效率的分布、形态、演化以及两极分化等问题做出基本判断，借此进行时空维度上的分析。具体公式为：

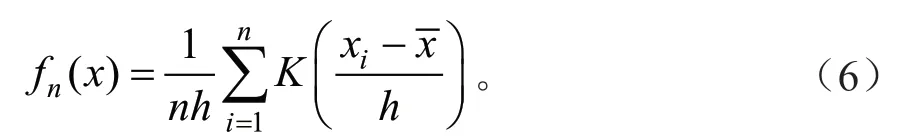
式中：n为样本观测值数量，为样本观测值均值，h为带宽，K(·)为核函数。在进行核密度函数估计过程中，需要选定合适的核函数与带宽。本研究选定Epanechnikov核函数，而相比于核函数，带宽的选取更为重要，故采用默认的最优带宽进行运算。

3.空间面板回归模型

空间面板回归模型将空间因素纳入到回归之中，可更好识别所研究单元的空间交互关系。目前使用较为广泛的是三种空间模型，分别为空间杜宾模型（SDM），空间误差模型（SEM），空间滞后模型（SAR）。本研究将通过相应检验对于模型的具体设置形式进行选择。

（二）效率测算指标体系构建

借鉴前人研究[15]，选用地区农业总产值为产出变量，劳动力、资本、水资源、土地资源、农药、化肥为投入变量，相应的指标及其解释如表1所示。其中农业劳动力投入难以找到具体数据，参考已有做法，用农林牧渔业从业人员数乘以农业产值占农林牧渔业总产值的比例，来确定劳动力投入水平[24]。本研究采取的基本估计模型为式（5），由于化肥和农药两项指标存在大部分数值小于1的情况，在取完对数后会存在投入指标为负数的情况，违背了本身的经济含义，故而本研究先对这两项指标取指数，在后续估计中取对数仍是其本身。本研究数据为2007—2018年全国30个省市区（港澳台藏由于数据缺失未进行分析）的面板数据，数据均来源于国家统计局和EPS数据库，少数缺失值运用线性插值的方法进行补齐。后续的回归分析数据亦是如此①数据来源网址：https://data.stats.gov.cn/easyquery.htm?cn=E0103，https://www.epsnet.com.cn/index.html#/Index。

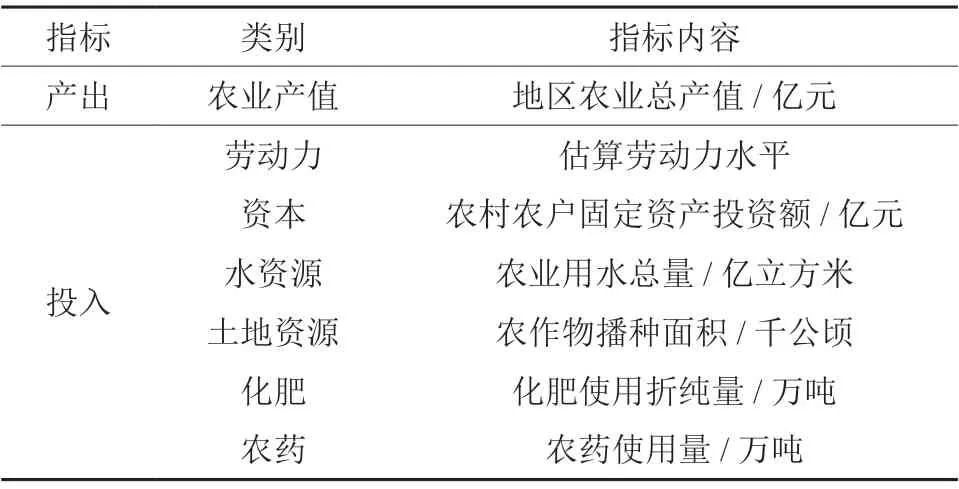
表1 农业资源效率投入产出指标体系

二、结果与分析

（一）SFA结果分析

运用Stata15软件对式（5）进行估计，考虑效率时不变和时变两种情形，得出的主要结果如表2所示。从结果可以看出η＞0且在1%的显著性水平上拒绝了原假设，因而适合选用时变模型，同时两个模型的γ值都较为接近1且均显著，表明实际产出偏离前沿水平并不是由白噪声造成，而是由生产无效引起的，因而适合使用SFA模型。而本研究选择的6个投入要素在时变模型中均在10%到1%的水平上显著，表明指标选取是较为合理的。且除了农药投入之外，其余要素的投入都会带来产出的增长，而农药的过量使用则会带来相反的结果。

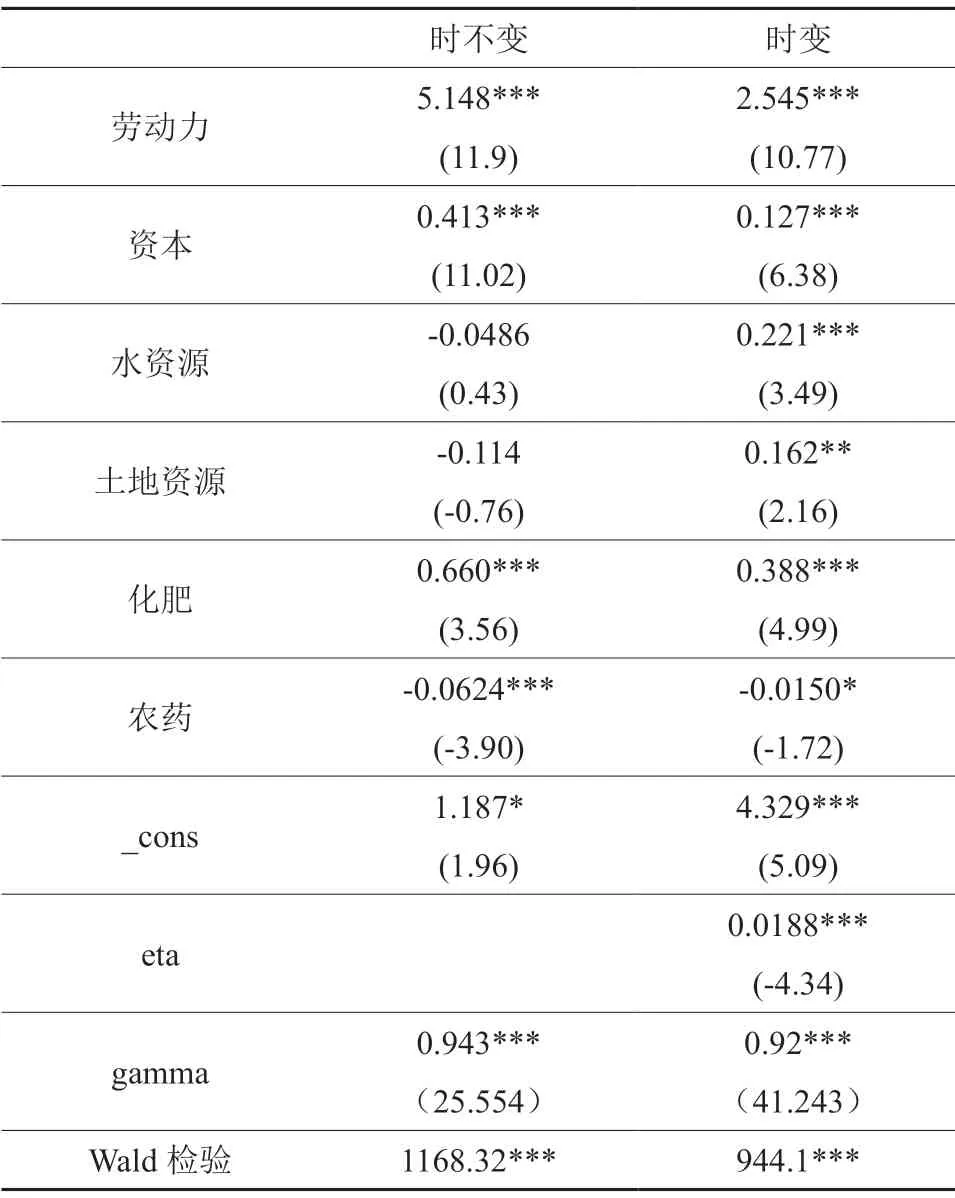
表2 面板随机前沿估计结果†

（二）核密度函数分析

在进行SFA估计后，可应用核密度函数对农业资源效率动态的变化特征加以分析（图1）。从位置上看，2007—2018年核密度函数整体向左迁移，表明我国农业资源效率水平呈下降趋势。从形状上看，各年的核密度函数没有严格的单峰状态，表明近年来我国农业资源效率出现两极分化状态，各省份农业资源效率分布具有一定的差异；从波峰的位置看，各年都是较为靠右的，表明在省份农业资源效率水平差异的基础上，大部分省份的农业资源效率属于较高的梯队之中；从峰度上看，有较强的宽峰特征，表明我国各省份的农业资源效率具有分异特征。

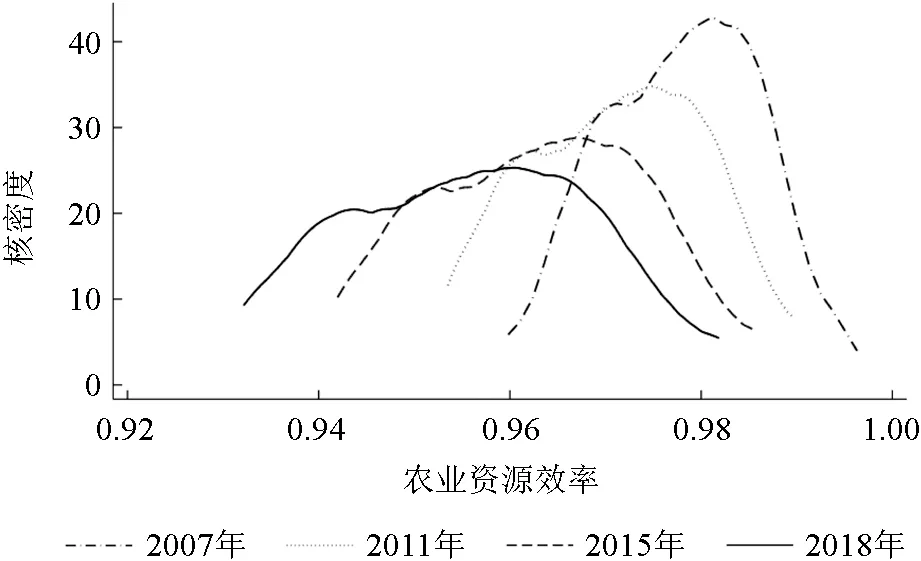
图1 2007—2018年中国农业资源效率核密度函数

总体来看，尽管我国农业资源效率的基准水平较高，但是均未能达到效率前沿面水平，存在着相应的提升空间，且在样本期内呈现下降之势，区域之间也存在相应的差异特征。自然资源受到损害，农药化肥等化学资源的过度使用都使得农业资源效率降低。因而新时期下，要更加切实遵循习近平提出的“绿水青山就是金山银山”的理念，以保障农业绿色健康的长久发展。

（三）空间面板回归模型构建及结果分析

1.全局莫兰指数计算

在建立空间面板回归模型之前，可对于农业资源效率的空间性质进行检验，选取全局莫兰指数进行分析，此指数可反映对象指标的空间整体相关程度。鉴于目前文献中对于莫兰指数的介绍与应用已较多，在此不做赘述。全局莫兰指数的测算结果如表3所示。从结果可以看出，2007—2018年农业资源效率的莫兰指数均在0.237～0.249之间浮动，均大于0且在1%的显著性水平上显著。由此表明我国农业资源效率存在空间上的正向相关性，即一地的农业资源效率与周围地区的效率是存在相互的正向影响，这在一定程度上也表明我国各省份的农业发展是存在空间相关性质的。

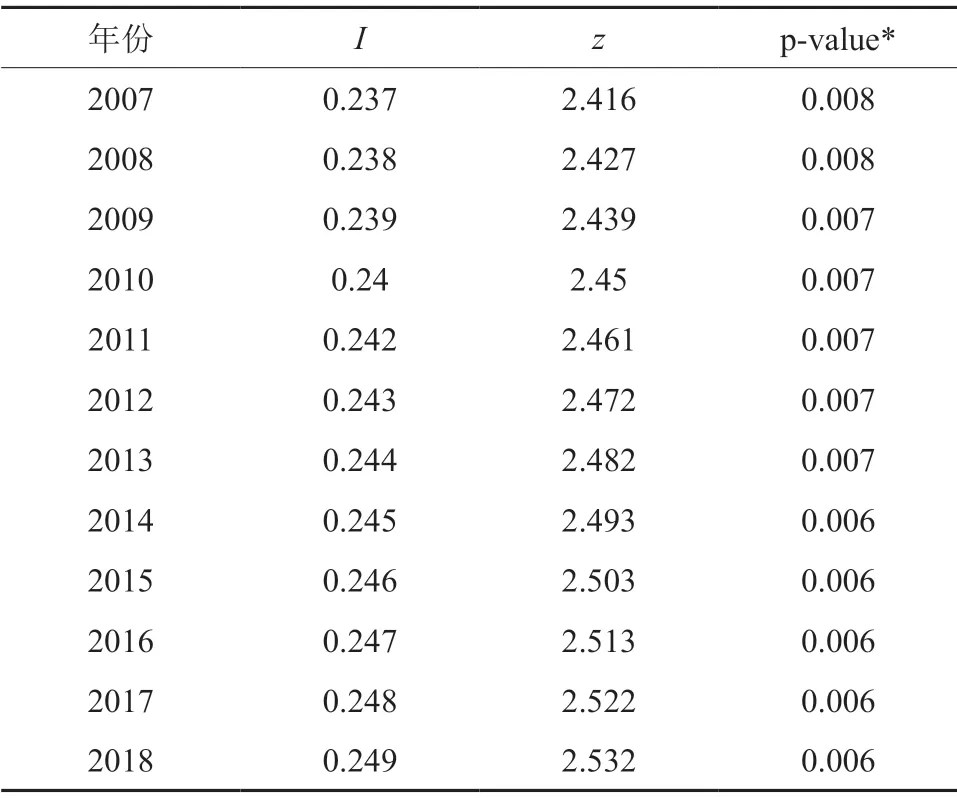
表3 2007—2018年农业资源效率全局莫兰指数

2.自变量选取

本研究回归模型中的被解释变量是农业资源效率，解释变量的选择依据主要是基于“宏观环境-农业特征-自然因素”系统，借鉴相关学者的研究成果以及数据的可获取性[21]。选择宏观环境：地区经济水平，城镇化水平，交通水平，教育水平；农业特征：农业机械化水平，农业财政支持；自然因素：自然环境特征。其中地区经济水平（pgdp)为地区GDP除以总人口并取对数。城镇化水平（urban）为城镇人口比上常住总人口。以上两个指标可反映地区整体经济的发展水平，对于农业资源效率的影响是不能完全确定的。在经济发展与城镇化过程中，会带来两方面的影响，一方面农村劳动力转移以及非农就业不利于农户农业劳动生产率的提高[10]，并且土地城镇化在一定程度上抑制农业生产效率的提高[25]。另一方面，地区的经济发展与城镇化进程都能够推动城乡之间的资源加速流动和有效配置，城镇的专业化部门能够为农业生产部门提供包括技术在内的各种先进的生产要素和科学方法[26]。交通水平（transport）为地方财政交通运输支出比上地方财政支出，本研究预期的系数结果为正。教育水平（education）为15岁以上人口的非文盲率，本研究预期的系数结果为正。农业机械化水平（mechanization）是地区农业机械总动力比上耕地面积，本研究预期的系数结果为正。农业财政支持（fiscal）为地方农林水事务财政支出比上地方财政支出，本研究预期的系数结果为正。自然环境因素（environment）是地区农业受灾面积，本研究预期的系数结果为负。

3.空间权重矩阵和空间面板回归模型构建

农业资源效率具有空间上的正相关性，本研究采用空间面板回归模型对农业资源效率的驱动因素进行研究。在构建模型之前，需要建立空间权重矩阵，由于农业发展有很强的地域限制，资源的流动速度较其他类型资源更慢，且随着地理距离的增大，农业上的相关性和资源流动的速效性是逐渐衰退的，故本研究首先选用了距离衰退的空间权重矩阵，即距离越远，空间相关程度加速变缓。并且出于稳健性考虑，本研究还构建了经济距离矩阵和嵌套矩阵，由此更能反映空间的多样特征，三种矩阵的具体构建方式和解释如表4所示。

表4 空间权重矩阵

在空间面板回归模型中，空间杜宾模型是空间自回归模型和空间误差模型的一般形式，在相应条件下可转化为后两种模型，且空间杜宾模型引入了因变量和自变量的空间滞后变量，能有效解决遗漏变量问题并分析自变量的空间溢出效应，因而具备更强的实用性，故本研究构建的基准回归模型为空间杜宾模型（SDM），如式（7）。式中，Y是被解释变量农业资源效率，X为解释变量，即上述选择的可能影响农业资源效率水平的7个变量，W是空间权重矩阵，ρ为被解释变量的空间自回归系数，β为解释变量的回归系数，θ为解释变量的空间回归系数，μi为个体固定效应，δt为时间固定效应，εit为不可观测的随机误差项。

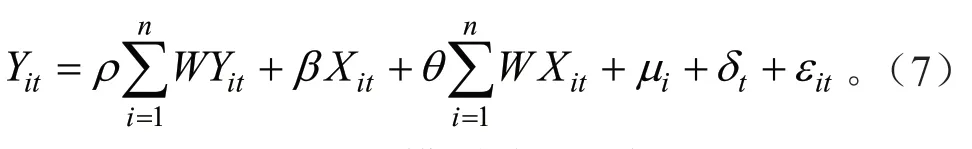
4.空间面板回归模型结果分析

本研究以距离衰退矩阵下的空间杜宾模型进行基础建模。首先运用空间计量下的Hausman检验判定选用固定效应还是随机效应模型，Hausman检验的结果为chi2(15)=33.78，Prob=0.003 7，表明在1%的显著性水平上拒绝选择随机效应模型的原假设，故选择双向固定效应模型。其次判定空间杜宾模型能否退化为空间滞后模型或者空间误差模型，运用LR和Wald检验对假设进行判定。LR检验的统计量结果分别为69.19和69.12，相应P值均为0.00，则表明在1%的显著性水平上拒绝原假设，SDM不能退化成SAR或者SEM。Wald检验的统计量结果分别为63.75和48.40，相应P值均为0.00，也表明SDM不能退化成 SAR或者SEM。依据检验结果选择SDM模型。表5报告了三种空间权重矩阵下的空间杜宾模型估计结果。

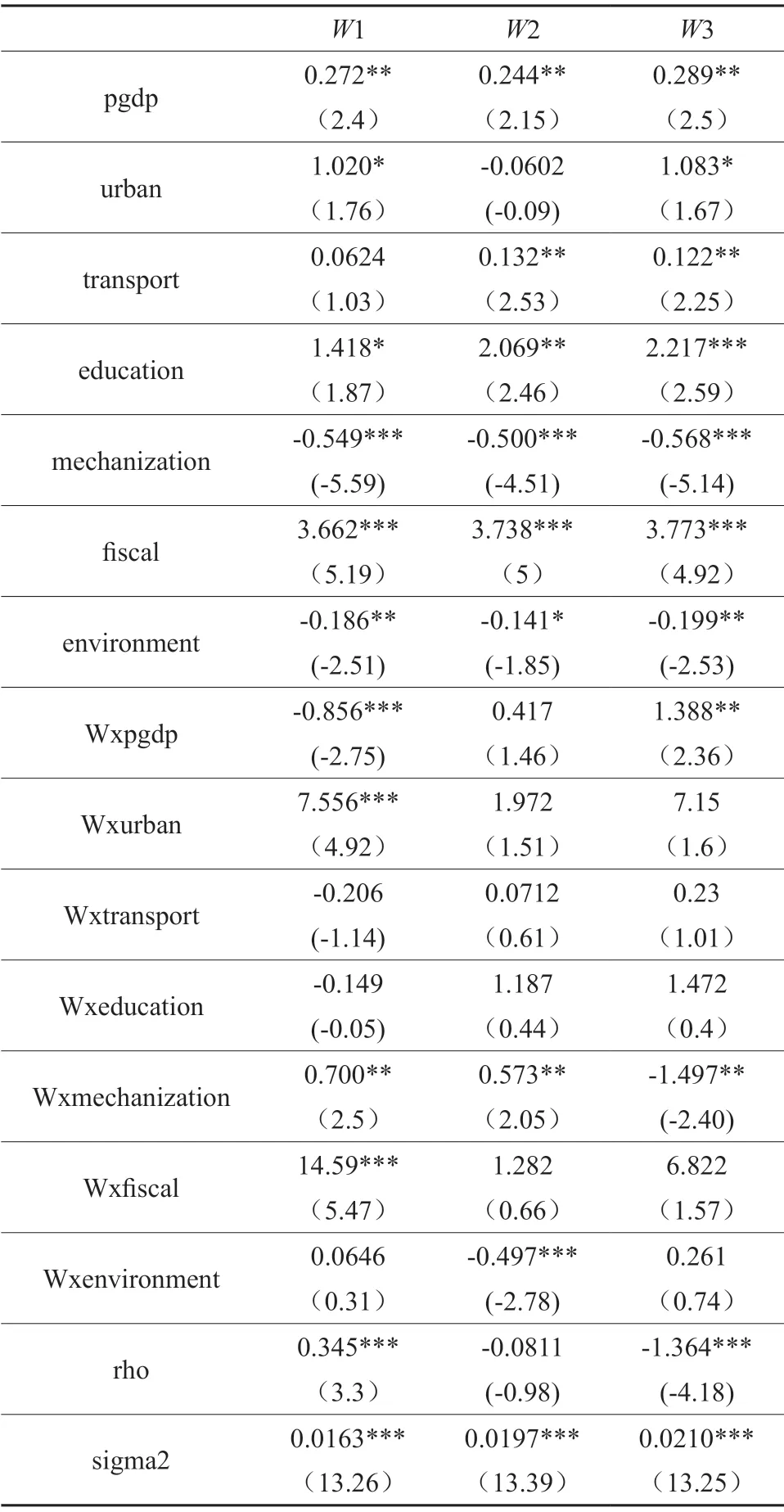
表5 SDM回归结果

从回归结果中可以看出，空间自回归系数pho在距离衰退矩阵和嵌套矩阵均为显著，且同时考虑经济和地理因素时，系数为正，表明农业资源效率存在正的空间溢出效应，与莫兰指数的测度结果相一致。

从具体影响因素来看，地区的经济水平与城镇化水平的回归系数皆为正，且均在5%或10%的显著性水平上拒绝原假设（除了在经济距离矩阵下，城镇化率的系数为负但是不显著）。表明经济水平的整体发展对于农业资源的利用效率还是有正向影响的。交通水平在距离衰退矩阵中系数为正但不显著，在经济距离矩阵和嵌套矩阵下系数为正且在5%的显著性水平上通过了检验，这与预期结果是一致的，表明在考虑了经济水平空间依赖性的情况下，交通越便利，越会使得农业资源的使用更加便捷，也使得农业资源的流动变得更加高效，从而提高了农业资源效率。教育水平系数为正且是显著的，这与预期结果一致，文盲率较高的情况一般发生在落后的农村地区，换言之，非文盲率越高，则代表区域内的整体受教育水平较高，而对于农民，受教育程度越高，则会在农业资源配置过程中更大限度地趋近科学性和有效性，使得农业资源效率水平也越高。农业机械化水平的系数为负且均在1%的显著性水平上通过了检验，这与预期结果是相反的。一般而言，农业机械化水平越高，代表农业更加现代化和规模化，则农业资源的效率水平也应当是越高的。出现本研究负向的情况可能原因在于，一是我国的农业发展还未能够呈现规模化的特征，那么农业机械动力的应用未能与农业规模水平实现较好地适配，故农业机械水平的提升并不能带来资源效率上的正面影响。二是本研究的指标测度或不能完全贴合现实，用地区农业机械总动力比上耕地面积虽然能反映单位耕地面积使用农业机械动力的情况，但是不能够对规模不同的农业生产者进行区分。这在后续的研究中是需要继续深化和优化的。财政支持的回归系数为正且均在1%的显著性水平上通过了检验，表明地方财政支持农业发展的力度越大，农业资源效率水平越高，这与预期结果是一致的。农业的发展不仅依赖于农民本身，也仰赖于政府政策的支持和实际的激励，因而财政支农会给农业资源配置的效率带来正向的影响。自然环境因素的回归系数为负且在10%或者5%的显著性水平上通过了检验，这与预期结果是一致的。本研究选取的度量自然环境因素的指标是地区农业受灾面积，若农业受灾面积越大，自然环境也就越差，致使农业生产不能够如预期顺利进行，由此资源配置效率也会降低。

从变量的空间滞后项来看，经济水平在地理衰退矩阵和嵌套矩阵下分别为负向和正向显著，表明经济发展对农业资源效率的影响在地理层面上可能具有“根植性”而阻碍对邻近省份的正向溢出，但是扩大到经济领域，由于经济发展的外部性则能够对于邻近省份的农业资源效率产生正向的影响。城镇化水平、财政支持以及农业机械化水平在地理衰退矩阵下也是产生正向的显著影响，表明在地理上这几个变量具有空间的正向溢出作用。自然环境因素在经济矩阵下为负向显著，表明有对经济发展水平相近省份的农业资源效率水平有负向抑制作用。

三、结论与建议

本研究运用了面板随机前沿模型测度了我国30个省（市、区）2007—2018年的农业资源效率，运用核密度函数方法分析了农业资源效率的时空分布与演变特征，最后运用空间杜宾模型对农业资源效率的驱动因素进行了回归分析，得出如下结论。

劳动力、资本、水资源、土地资源、农药、化肥等要素作为投入变量对于农业产出都是具有显著的影响作用，除农药外，都可带来正向的促进作用。我国整体的农业资源效率的基准水平较高，不过还未能达到前沿面的效率水平，仍具有一定的提升的空间。

我国农业资源效率水平具有随着时间的推进，不断呈现下降趋势的特征，而造成这个现象的主要原因可能在于我国的农业自然资源受到了相当程度的损坏，化肥、农药、农膜等具备一定化学要素的农业资源的不当使用使得环境污染严重，而又使得农业资源效率下降。并且农业资源效率水平虽然具有空间上的相关性，但是也存在着相应的差异特征，地区之间呈现发展不平衡的状态。

在驱动农业资源效率的因素之中，基于三种权重所构建的空间杜宾模型的估计结果在整体上保持一致。总体而言，地区的经济、城镇化、交通、教育、财政支农等因素的水平越高，则越能提高当地的农业资源效率水平。自然环境越恶劣，则农业资源效率水平越低。在本研究中，农业机械化水平越高，农业资源效率水平反而越低，本研究认为可能的原因在于指标度量的偏误以及农业生产规模与农业机械化的不完全适配。

基于如上结论，本研究提出相应的政策建议，以期能够为我国的农业资源的利用效率水平以及我国农业的绿色健康的长期发展提供具有建设性和科学性的决策参考。

第一，在农业发展过程中，整合多种要素，积极促进流动。农业产出与资源效率水平的高低受多种资源的影响，需根据地区情况合理引入和配置资源要素，以促进农业资源效率的提高。劳动力、资本、水资源、土地资源、化肥等要素的合理投入都会带来资源效率的提高，因而可依据相应区域的实际情况制定使用标准，引导农民合理利用资源要素，避免过度滥用。

第二，农业的发展离不开环境的保护和优化，要切实遵循习近平提出的“绿水青山就是金山银山”的科学论断，保护好农业生态环境，主要地要继续大力发展绿色农业，避免农药滥用致使土壤和河流环境受到伤害，由此也会带来效率水平的提升。

第三，经济发展与城镇化进程是与农业发展并行不悖的，但是需要着重协调好各自之间发展关系，以此缩小城乡差距，从而推动农业资源的优化配置。政府应着力加大交通、财政、教育方面的投入，由此带来的不仅是区域内整体发展的提升，也会促进农业资源效率的提升。同时要优化农业规模结构，以此适配各地区的机械化和农业现代化水平。最后，应当建立预设性的防灾救灾机制，避免因非预期的自然灾害所带来的资源效率水平的降低，最终也避免农业的发展受到过大的冲击。