垂直轴风力机翼型涡流噪声的数值分析

杨从新，宁健斌，李寿图

(1. 兰州理工大学能源与动力工程学院，甘肃 兰州 730050； 2. 甘肃省风力机工程技术研究中心，甘肃 兰州 730050；3. 甘肃省流体机械及系统重点实验室，甘肃 兰州 730050)

随着全球变暖和能源危机的情况逐步严重，对于可再生能源的利用愈发显得重要，而风能是1种可再生的绿色能源且储量丰富，是目前最具商业化发展前景的能源.而垂直轴风力机由于性能好、尺寸小等优点，安装位置距离居民区越来越近，带来的噪声问题日益凸显[1]，因而气动噪声的研究迫在眉睫.风力机气动噪声是由风力机叶片与远前方空气来流相互作用产生的，根据产生原因的不同大致可分为三大类: 低频噪声、来流湍流干扰噪声、叶片自噪声.

国内外学者均对气动噪声做了大量的试验测试和数值研究.JONES等[2]利用直接噪声模拟方法(CAA)对NACA0012翼型气动噪声进行了计算，研究了翼型在4个攻角下的翼型自噪声特性.TAKAGI等[3]和CHONG等[4]分别对NACA0018和 NACA0012进行了风洞试验，得到其在特定雷诺数下的气动和声学特性.LUMMER等[5]研究了对称翼型在0°攻角下的气动噪声，发现尾缘脱落涡会对声学信号产生影响.GHASEMIAN等[6]利用LES与FW-H相结合的方法研究垂直轴风力机气动噪声，研究发现偶极子声源占主要影响.MOHAMED[7]提出了1种具有3个双翼叶片的垂直轴风力机模型，可以降低噪声污染.在国内，白悦荻等[8]也利用数值模拟对翼型与来流相互作用产生的噪声进行了研究.

目前相关研究大都集中于水平轴风力机翼型上，关于垂直轴风力机翼型气动噪声的研究较少.文中利用Fluent中的分离涡模拟方法(DES)进行流场模拟，将气动性能的数值结果与试验结果进行验证，再通过建立声学类比噪声方程进行预测，研究不同攻角和不同雷诺数下对该垂直轴风力机翼型气动性能和气动噪声的影响.研究将有助于确定气动垂直轴风力机翼型气动噪声产生的机理，以及了解涡流对气动噪声的整体影响.

1 试验设备及数值方案设计

1.1 试验风洞

试验的西北工业大学风洞是1个开放式回路、闭环测试、低速低湍流风洞，如图1所示.矩形测试段为400 mm×1 000 mm，长度为2 800 mm,最大风速为70 m/s.湍流强度可调节范围在0.02%～1.00%，在尾耙处，设有4个静压测量管，120个总压测量管.风速在12,15,30 m/s下分别对应的湍流强度为0.030%,0.025%,0.020%[9]，风速误差小于±3%.图2为该翼型试验时装配设置示意图.通过调节翼型攻角和风洞风速，利用连接测量器的装置，将试验数据传送至电脑进行处理分析.

图1 试验风洞剖面示意图

图2 LUT试验翼型示意图

1.2 数值计算设置

该试验翼型模型弦长c=200 mm，如图3所示，计算域由半圆域加矩形域组成，在ICEM中构造结构化网格.其中，速度入口为15c的半圆形区域，尾迹出口为20c×30c的矩形区域.图4为计算域全局与局部网格的分布情况，计算域网格总数为10.3万.在翼型的前缘、尾缘、压力面和吸力面均进行了网格局部加密处理，以保证y+<1.如图4所示，翼型外第一边界层网格厚度为0.013 4 mm，网格的增长率设为1.1，翼型网格质量满足数值计算要求，将外边界设置为压力远场，翼型设为无滑移壁面.

图3 流场计算域示意图

图4 计算域全局网格及局部网格划分

1.3 噪声监测点分布设置

为了研究翼型的声压级指向性特征，如图5所示，监测点以翼型0.5倍的弦长处(点O)为中心，在以半径分别为1c，2c，3c，4c，5c的圆上沿圆周方向以每隔15°设置为一个监测点，共设置有120个噪声监测点.另外在翼型周围设置了4个监测点，分别位于尾缘的后部和上方，如图5b所示.其中，点A和点B分别位于尾缘后部2c和5c位置处，点C和D分别位于翼型的尾缘上方5c和10c位置处.而为了研究翼型4个方向上总声压级的分布规律，同样是以翼型的0.5倍的弦长处(点O)为中心，在翼型的尾缘、上翼面、前缘、下翼面4个方向上分别以间隔1倍弦长的距离设置为1个监测点，共设置有40个监测点用来计算翼型四周监测点的总声压级.

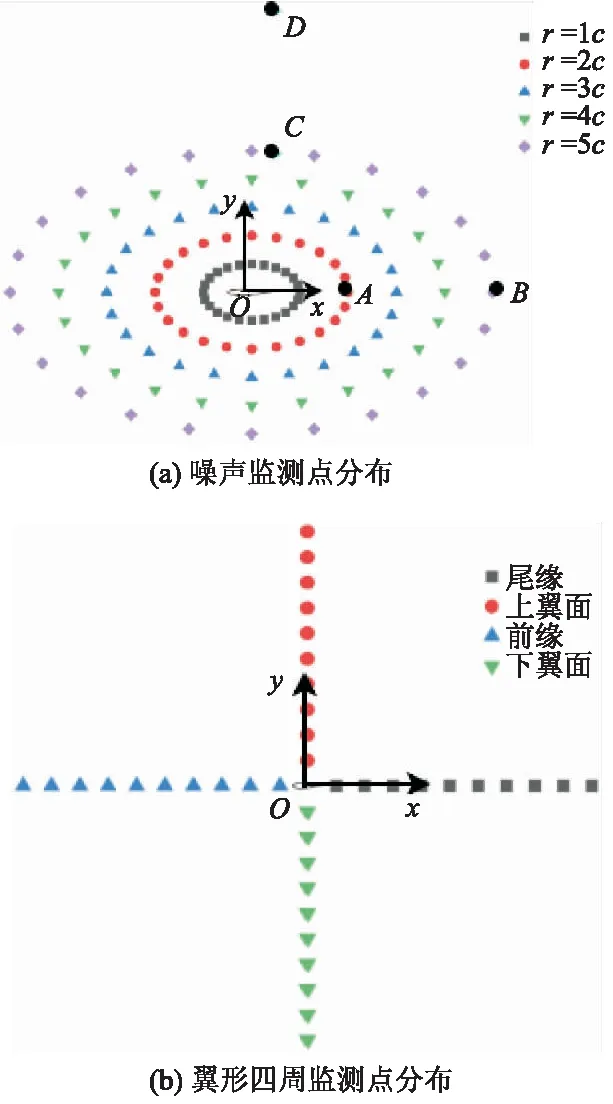
图5 翼型噪声监测点设置示意图

1.4 计算边界条件的设置

工质设为理想气体，采用速度入口，计算速度分别为23 m/s和40 m/s，计算雷诺数分别为3.0×105和5.0×105；采用压力出口，定义出口压力相对大气压力为0；流场计算先采用SST模型进行稳态计算，收敛后再采用DES模型进行非稳态计算，DES模型中近壁面的附面层采用的是RANS方法中的SSTk-ω模型.采用SIMPLEC算法，时间步长设为5.0×10-5s，在计算瞬态4 000步后，当翼型升阻力系数达到稳定时，再设置4 000步用以计算流场时域数据，采集流场数据及声源数据，共计算8 000步，结束时间为0.2 s.

2 数值模拟模型

2.1 DES湍流模型

文中首先是利用分离涡模型DES对翼型周围的脉动压力进行计算，再利用Lighthill声类比方法对翼型周围声场进行计算，设置噪声监测点，最后提取计算声场的监测点数据进行分析.

分离涡模拟方法是(RANS/LES)混合模拟方法，该方法在近壁区采用了RANS方法模拟，在远离壁面的主流区采用LES方法模拟，该方法兼顾了RANS和LES各自的优势.最早的DES形式是基于Spalart-Allmaras模型的DES，其表达式为

(1)

式中：d为长度尺度.

(2)

(3)

(4)

2.2 FW-H方程

基于FW-H方程求出

(5)

式中：p′为声压；ni为表面法向量；vn为法向速度；C0为声速；Tij为Lighthill应力张量.等式右侧3项分别代表四极子、偶极子噪声和单极子.文中模型表面可看作是刚性的，由固体边界体积位移引起的单极子噪声近似为0；低流速下由流体内应力引起的四极子噪声也可忽略不计；文中重点考察由模型表面脉动压力引起的偶极子噪声.

3 结果与分析

3.1 气动性能的有效性验证

为验证该翼型的有效性，对翼型的气动性能进行计算，计算雷诺数Re=3.0×105，来流速度为23 m/s，将数值计算所得数据与试验值进行对比.图6给出的是该翼型在不同攻角α下的升力系数CL和阻力系数CD的试验值与计算值.由图可知，模拟的升力系数在附着流域基本与试验值相吻合，在失速域略大于试验值，而模拟的阻力系数略小于试验值，但变化趋势总体吻合良好.

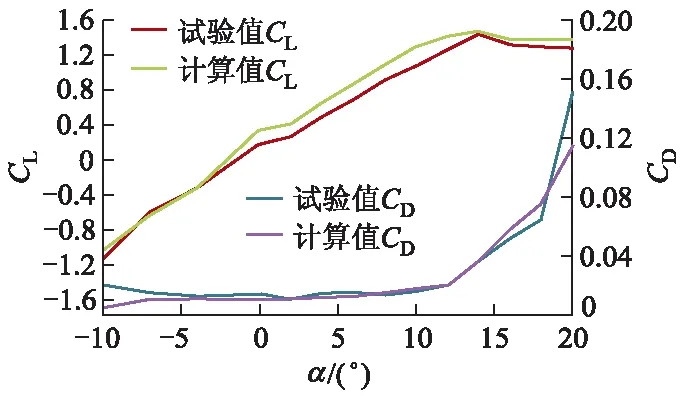
图6 翼型的升阻力系数试验值与计算值对比

同时选用了2种不同的湍流模型(SSTk-ω,S-A)对不同攻角下的翼型的表面压力系数进行数值模拟.图7为不同攻角下的压力系数CP拟合分布曲线与试验值的比对，图中x/c为截面不同点的横坐标弦长.由图可知2种湍流模型都具有较好的拟合结果.在小攻角范围内，计算值与试验值的两者拟合曲线较为接近.而在大攻角下，流动易发生分离，导致流动结构复杂多变，使计算结果与试验值偏差较大.综上所述，说明建立的模型、网格质量和边界条件合理，计算结果准确有效.

图7 不同攻角下的压力系数CP试验值与计算值拟合分布曲线

3.2 气动噪声特性分析

3.2.1 不同攻角对翼型气动噪声的影响

图8为不同攻角下翼型的声压级SPL指向性分布特性图.由图可知，所给出的攻角下，翼型声压级大小均随着半径增大而逐渐减小.根据翼型的自噪声理论，翼型的噪声主要是以偶极子源为主，而图中的声压级指向也是呈现偶极子形状，证明结论与理论相吻合.同时随着攻角的不断增大，翼型的上下表面压差逐渐增加，压力脉动值也随之增大，因此声压级差值也跟随增加.由图7可知在攻角为 0°～8°内，翼型未出现较大的流动现象，属于自由平缓过渡状态，主要声源位于尾流中，这和其速度涡量图有很好的对应.因而声压级也是平缓增加，沿着x轴具有较好的对称性.同时由图7可知翼型在攻角为14°时开始失速，而随着攻角的增大，翼型吸力面上的涡脱落的位置逐渐向前缘推进，从而使产生的分离涡流噪声的位置也向翼型前缘推移，因此位于翼型尾缘的声源区在吸力面上向翼型前缘靠近，翼型的声压级数值也随着增大，声压级数值增加幅度也跟着迅速加大，并且声压级数值没有沿着x轴对称，此声压级在圆周方向的分布偏转了近30°.根据翼型声压级在周向上的分布情况，在小攻角范围内，声压级数值在翼型四周基本沿y轴对称，并且在2c至5c距离间差异不大，而与1c距离的声压级差异较为明显.

图8 各攻角下的翼型噪声声压级指向性

图9为翼型在4个不同方向(翼型尾缘、翼型上表面、翼型前缘、翼型下表面)上的总声压级分布规律图.从图中可知，翼型的上下翼面声压级数值大小基本相同，且声压级数值较明显大于尾缘与前缘，而翼型前缘处声压级大于尾缘处声压级.随着攻角增大，4个方向处声压级均增大，距离越远，声压级也随之逐渐减小.在攻角4°～8°内，翼型开始产生涡流，翼型的上下表面及尾缘处声压级增加幅度较大，而前缘处声压级依然是逐渐增加.随着攻角的增大，翼型开始失速直到翼型的吸力面发生分离，翼型尾缘处旋涡脱落的位置也随着攻角增大而逐渐沿吸力面往前缘靠拢，同时在翼型尾缘的右后方出现涡脱落，尾缘右后方的旋涡数量也随着逐渐增多，因而翼型的上下翼面声压级随之增大.

图9 翼型四周噪声监测点

3.2.2 不同雷诺数对翼型气动噪声的影响

选取雷诺数分别为1.0×105,3.0×105,5.0×105计算翼型在α=8°,r=2c,r=5c时的噪声指向性特征，如图10所示.从图中可以看出随着雷诺数的增大，声压级增幅较大，雷诺数Re=3.0×105时的声压级较Re=1.0×105时大近20 dB，翼型周围声压级指向也是呈现偶极子特征.而雷诺数为5.0×105时，声压级却降低了10 dB，但翼型周围声压级在不同雷诺数下仍然是偶极子声场特性.

由图10可知，声压级较大峰值均存在于低频区，低频偶极子声场特性明显.由于雷诺数增加，涡脱落愈发明显，翼型上翼面呈现较大声压级，并且在高频区域出现了小幅度的震荡.因此，合理的控制该翼型的雷诺数有助于用于降低适用叶片的噪声.

图10 噪声监测点的声压级频谱图

4 结 论

1) 通过翼型的气动性能试验数据与数值计算数据相互验证，证明了以分离涡模拟方法和声比拟方法建立的噪声预测方法的可靠性.

2) 声压级指向性图表明该翼型在不同攻角下都具有低频偶极子声场特征，也符合翼型的自噪声理论原理.

3) 该翼型的噪声特性与雷诺数关联较大，随着雷诺数的增加，翼型周围的声压级先是增加而后减小.因此合理的控制雷诺数，有利于降低该翼型的噪声，也为选择应用于低噪声叶片提供理论基础.