过渡流下近壁双圆柱倾角对绕流结构影响

尹广洲，邓勇，周磊，谢纬安，喜冠南*

(1. 南通大学机械工程学院，江苏 南通 226019； 2. 南通职业大学汽车与交通工程学院，江苏 南通 226007)

近壁圆柱绕流不仅是重要的理论基础研究，在实际工程中也具有广泛应用.例如在海底管道铺设中，通过设置管道之间以及管道与海底面的距离，来减小海水对管道的破坏[1].在核反应堆冷却中，通过布置核反应棒位置以加快热转换；以及在换热器的设计中，通过改变圆柱的插入角度来提高翅片的换热效率等[2].为了解决这些问题，对近壁圆柱绕流结构的研究具有重要意义.

国内外的学者对近壁圆柱绕流展开了许多研究.近壁单圆柱方面，1987年，BEARMAN等[3]在试验中发现，近壁单圆柱绕流尾迹主要受雷诺数和间隙比的影响.LEI等[4]在湍流状态下进一步对近壁单圆柱绕流进行了试验研究，发现随着间隙比的变化，圆柱尾迹会出现3种流动模式，且不同流动模式出现的临界值主要取决于壁面边界层[5]厚度.许慧等[6]、王丽娟等[7]分别对近壁单圆柱进行了模拟研究，分析了圆柱对壁面强化传热的影响.过渡流状态下，周磊等[8]试验研究了不同间隙比对近壁单圆柱尾流流动形态的影响，发现在间隙比为0.6时，壁面对圆柱尾流的流动特性影响显著.近壁多圆柱方面：随着圆柱数量的增加，圆柱尾迹不仅受到壁面的影响，还受到圆柱间的相互作用，因此尾流结构更加复杂.近壁串列圆柱尾流的涡脱频率与串列双圆柱有些类似，由于壁面的影响，尾迹特性有所不同[9-10].陈波等[11]分别对近壁串列和并列双圆柱进行了PIV试验研究，通过改变圆柱中心距和间隙比，给出了圆柱尾迹特性和斯特劳哈尔数的变化.在湍流状态下，RAIOLA等[12]进一步对近壁串列双圆柱进行了试验研究，总结了间隙比对下游圆柱尾迹特性的影响规律.

总体上，近壁插入圆柱绕流的试验研究主要集中于单圆柱和串并列双圆柱，研究成果丰硕.文中在前人研究基础上进一步探索，固定上游圆柱位置，通过改变下游圆柱与壁面的距离，使双圆柱与壁面间形成一定的倾角，称该倾角为近壁双圆柱倾角γ.在过渡流下对近壁双圆柱倾角模型进行试验研究，总结倾角γ对圆柱绕流结构的影响，可为实际工程中换热器的设计提供一定的理论指导.

1 试验方法

1.1 试验台介绍

图1为开式循环水槽试验台，其长宽高分别为3 000，300，300 mm，试验段水深为265 mm，为了保证水槽的透光性，其侧壁和底面均采用亚克力材料.试验台主要由6个部分组成，分别为下水箱、上水箱、整流段、收缩段、试验段以及回流段，回路中的配件包括：蜂窝器、隔膜阀以及潜水泵.

图1 开式循环水槽试验台

试验台水循环的过程：① 潜水泵将水从下水箱抽至上水箱；② 水从上水箱流出，经过隔膜阀调速后流入整流段；③ 水流经过蜂窝器整流后流入收缩段；④ 经过收缩段加速后，水流流入试验段；⑤ 通过试验段的水流再经过回流段，最终流入下水箱，完成整个循环.

1.2 PIV测试系统及试验模型简介

图2为PIV系统与近壁双圆柱倾角试验台的布置关系示意图.其中，PIV系统的硬件包括激光器、冷却器、同步控制器、CCD相机、计算机等；软件包括粒子图像测速系统、成像系统、数字相机控制系统等.试验中，激光采用Beamtech公司生产的双频脉冲激光器(Vlite-Hi-100)，使用PowerView2MP相机拍照采集样本，系统采样频率为20 Hz，每个样本工况拍摄400张.

图2 近壁双圆柱绕流试验台PIV系统示意图

1.3 试验模型简介

研究中，雷诺数定义计算公式为

(1)

式中：ρ为流体密度，kg/m3；U为流体的平均速度，m/s；D为圆柱直径特征长度，mm；μ为黏性系数，Pa·s.

图3为近壁双圆柱倾角试验模型图.其中，U0为进口速度，C为圆柱底部距壁面的距离，T为两圆柱横向中心距，C/D称为间隙比，T/D称为横向间距比，γ为近壁双圆柱倾角.

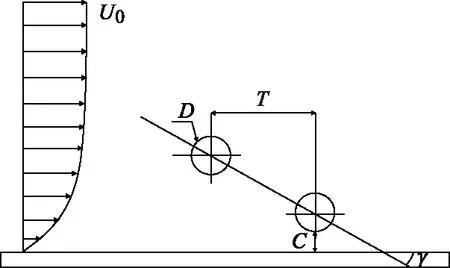
图3 试验模型示意图

1.4 试验方法简介

试验中，雷诺数为300，水温为25 ℃，圆柱直径D为15 mm.试验前，保持上游圆柱距离进口的位置为20.0D，通过改变下游圆柱与壁面的距离来调整倾角，分别取倾角γ为-11.3°，-7.6°，-3.8°，0°，3.8°，7.6°，16.7°和25.0°，并在流场中加入镀银玻璃球(直径为13 μm)作为示踪粒子.试验中由激光器从上方打出与水平面垂直的片状光源，结合CCD相机拍摄流场区域，最终通过Insight4G处理获得速度场图.

2 结果与讨论

为了研究倾角γ对圆柱绕流结构的影响，从速度流线及速度场、截面速度以及周期性角度进行分析.在近壁单圆柱的研究中，间隙比为0.6D时，壁面对圆柱尾流的流动影响较为显著[8]，因此文中保持上游圆柱间隙比为0.6D，通过改变下游圆柱位置来调整倾角γ，研究不同工况下的时均和瞬时流动特性.

2.1 时均流动特性

图4所示为Re=300，T/D= 3时，不同倾角下的时均流线图.

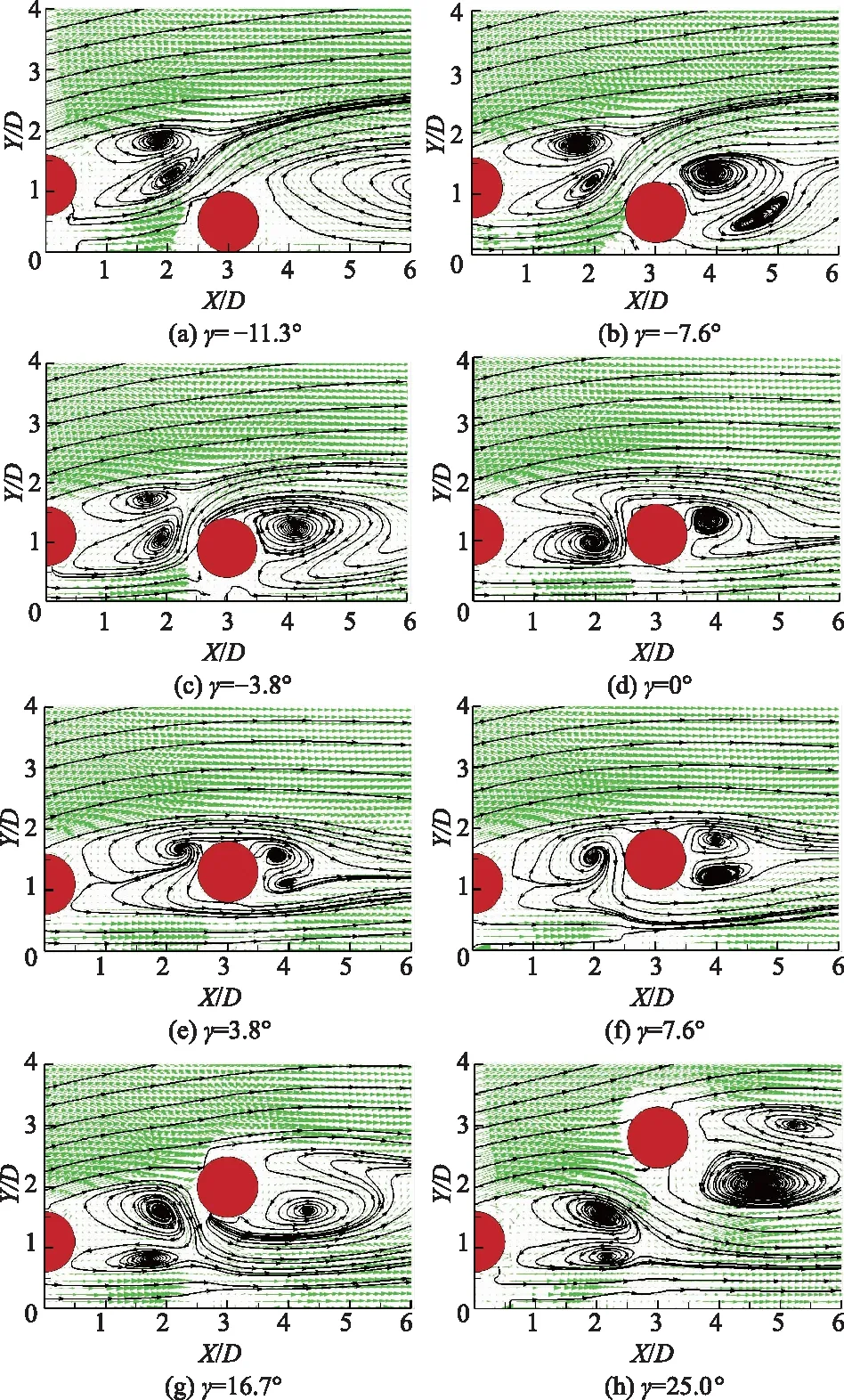
图4 Re=300不同倾角γ的时均流线及速度场图

具体分析当γ= -11.3°时，上游圆柱的剪切层在圆柱间形成了尺度相近的旋涡对，并向右上方倾斜.下游圆柱紧贴壁面，其上侧剪切层在下游壁面重新附着，形成顺时针旋转的大尺度旋涡.随着倾角γ增大到-7.6°，-3.8°，下游圆柱离开壁面，上游圆柱尾流受到下游圆柱的抑制效果逐渐增强，两圆柱间旋涡对受到挤压.下游圆柱与壁面间出现间隙流，且流量逐渐增大.在圆柱与壁面的相互作用下，圆柱尾流先出现旋涡对，再演变为上侧剪切层单侧绕流.当倾角γ为0°时，两圆柱位于同一直线上，下游圆柱抑制作用加强，上游圆柱的上侧剪切层发展受到抑制，表现为下侧剪切层单侧绕流.下游圆柱尾流依旧表现为上侧剪切层单侧绕流，但旋涡尺度明显减小.随着倾角γ增大到3.8°，7.6°时，上游圆柱位置开始低于下游圆柱，其下侧剪切层的发展受到抑制，圆柱间被上侧剪切层形成的旋涡充满.下游圆柱尾流在双侧剪切层的共同作用下，形成对称旋涡对.说明在该工况下，下游圆柱上下游剪切层的作用效果相同，处于相对平衡的状态.当倾角γ继续增大至16.7°，25.0°时，壁面和上游圆柱对下游圆柱尾流的影响逐渐减小，下游尾流开始由下游剪切层的单侧绕流逐渐演变为旋涡对.同样，上游圆柱受下游圆柱的影响也在减弱，其尾流逐渐演变为近壁单圆柱的情况.

总体上，随着倾角γ不断增大，上游圆柱尾流由下侧剪切层发展被抑制逐渐演变为上侧剪切层发展被抑制，圆柱间由旋涡对先变为单侧绕流再演变为旋涡对；下游圆柱开始由上侧剪切层占主导，在γ=7.6°时达到平衡，再演变为下侧剪切层占主导，最终趋于单圆柱绕流情况.

图5 速度截面位置示意图

图6 Re=300时不同倾角的速度截面图

在X/D=4，5位置处，近壁区域未出现速度波峰，速度大小减弱，说明壁面附近形成大尺度旋涡的运动速度较小.随着倾角γ增大到-7.6°，-3.8°，下游圆柱与壁面间有流体通过，速度波峰出现并逐渐增大.流体在X/D=4，5壁面附近获得加速，但由于壁面黏性剪切力作用，速度小于上侧剪切层，此时上侧剪切层起主导作用，表现为下游圆柱尾流由上大下小的旋涡对变为上侧剪切层单侧绕流.由于下游圆柱离开壁面，不再堵塞上游近壁区域的来流，X/D=1，2处速度波峰有所增加，即壁面附近流体获得略微加速.在倾角γ=0°时，上游圆柱的X/D=1，2处速度波峰进一步增加，说明下侧剪切层起主导作用，表现为下侧剪切层单侧绕流.下游圆柱受壁面剪切力的影响开始减弱，近壁区域流体速度得到进一步增大.倾角γ继续增大，下游圆柱尾流逐渐脱离了壁面影响，近壁区域流体速度继续增加.在倾角γ=7.6°时，上游圆柱近壁区域速度波峰减小，流体速度开始减弱.下游圆柱两侧剪切层的加速效果相同且达到最大值，在上游圆柱和壁面的共同作用下，下游圆柱尾流形成完全对称的旋涡对.当倾角γ=16.7°，25.0°时，上游圆柱尾流的速度波峰基本不变，流体速度趋于稳定，说明其受到下游圆柱的影响逐渐较小.下游圆柱近壁区域加速效应维持的区域增大，表现为圆柱尾流旋涡尺度增大.可以推测，当倾角γ继续增大时，下游圆柱将不再受到壁面和上游圆柱的影响，其后方的速度截面分布趋于对称.

总体上，随着倾角γ的增大，上游圆柱的上侧剪切层获得加速且基本保持不变，下侧剪切层加速效果先增强后减弱.受上游圆柱和壁面的影响，下游圆柱上侧剪切层的加速不断增加直到稳定，下侧剪切层加速效果先增强最终稳定，而加速效应维持的区域不断扩大.

2.2 瞬态流动特性

过渡流状态下，流场具有周期性变化规律[13-14].从文中分析可以看出，倾角γ=-7.6°时，壁面与圆柱间影响明显，此时，上下游圆柱尾流均出现旋涡对，能初步判断圆柱尾流具有较明显的周期变化规律.为了进一步理清周期性特征引起近壁区域的流动不稳定性机理，以下选取倾角γ=-7.6°工况，结合圆柱尾流一个合理监测点在y方向的速度脉动图进行分析.

图7为监测点的位置示意图，监测点分别位于上下游圆柱尾部.监测点A与上游圆柱最高点的横向间距x1为2.0D，与壁面的纵向距离y1为1.6D；监测点B与下游圆柱最高点的距离x2为1.5D，与壁面的纵向距离y2为1.2D，以确保监测点能顺利捕捉到圆柱尾流的速度脉动.

图7 监测点位置示意图

图8为监测点在y方向的速度及其能量谱密度，其中监测点A，B的能量谱密度均出现了峰值，这表明上下游圆柱尾流具有一定的周期性流动规律.监测点A在y方向上的速度脉动形成单一峰值，说明上游流场具有明显的周期性特征.监测点B的能量谱密度出现了2个峰值，说明下游流场的周期性较弱，这是因为下游圆柱尾流不仅有上游圆柱尾流的干扰，还受到壁面的抑制作用，导致其尾流的流动特性更加复杂，周期性流动特征较弱.

图8 监测点在y方向的速度及其能量谱密度

基于对γ=-7.6°工况下速度及其能量谱密度图的分析，以下详细分析一个周期内圆柱尾流的瞬时流动特性.图9为上下游圆柱尾流在一个流动周期内的瞬时流线及速度场图.

从图9中可以看出，周期开始时(T0=0.125T)，上游圆柱下侧初步形成逆时针旋转的小尺度旋涡，上侧为正在发展的大尺度旋涡，伴随着上侧旋涡不断向后移动直至最终脱落，下侧小尺度旋涡也紧随其后，不断发展，尺度逐渐增大，最终脱落.周期结束时(T0=T)，下侧再次形成一个新的小尺度旋涡，上侧同样为正在发展的大尺度旋涡，即将发展成周期开始的状态，完成了一个周期的流动.对比之下，下游圆柱尾流的周期性特征不太明显.下游圆柱的上侧旋涡先增大后减小，最终消失.与此同时，下侧旋涡也在向后移动并消失，且下侧旋涡的脱落速度要快于上侧.正是由于这种周期性的旋涡脱落，使圆柱尾流的扰动加剧，从而增强了近壁区域的流动不稳定性.

图9 Re=300时一个流动周期内的瞬时流线及速度场

3 结 论

1) 近壁双圆柱倾角对绕流结构影响显著.随着倾角γ的增大，上游圆柱尾流受到下游圆柱的抑制角度也在变化，由下侧剪切层发展被抑制逐渐演变为上侧剪切层发展被抑制；下游圆柱尾流由上侧剪切层主导逐渐演变为下侧剪切层主导.

2) 壁面附近扰动程度与近壁双圆柱倾角的大小有关，随着倾角γ的增大，上游圆柱近壁区域的加速效果先增强再减弱，壁面附近流动不稳定性先增强后减弱.下游圆柱近壁区域加速效果不断增强直至稳定，加速效应维持的区域不断增大，壁面扰动程度增强.

3) 在文中研究的工况中，近壁双圆柱倾角对绕流结构具有一定的影响，在γ<7.6°的工况下，倾角γ对绕流结构影响逐渐增大；在γ>7.6°的工况下, 倾角γ对绕流结构影响逐渐减弱.

4) 过渡流下流场具有周期性特征，在倾角γ=-7.6°工况下，上游圆柱尾流流动的周期性要强于下游，两圆柱尾流形成周期性的旋涡交替脱落，增强了壁面的流动不稳定性.