理想状况下涡流发生器尾涡特性

2021-12-06田晓庆王刚王海洋朱泽飞潘华辰冷建兴

排灌机械工程学报 2021年11期

田晓庆,王刚，王海洋,朱泽飞*,潘华辰，冷建兴

(1. 杭州电子科技大学机械工程学院，浙江杭州 310018; 2. 浙江大学海洋学院，浙江舟山 316021)

涡流发生器最早应用在航空领域，是一种结构简单、形状多样的边界层控制装置[1].涡流发生器可以把能量较高的流体和边界层处能量较低的流体混合，以增大边界层的能量，达到延迟边界层分离的目的[2].近年来, 涡流发生器在水动力学中的应用研究也逐渐展开.田晓庆等[3-4]运用SST模型和尾水管效率测量的方法对包含涡流发生器的试验尾水管和家用小型水轮机尾水管中的水流特性和尾水管性能进行了研究.任勇翔等[5]采用k-ε模型对安装于漏斗式反应器中的涡流发生器进行研究，并结合水力特性进行了试验，证明涡流发生器能较好地将药剂和水混合，显著提高水处理效果.马光飞等[6]采用欧拉模型中的VOF法，对涡流截流装置进行了数值模拟，并用相机记录了安装涡流发生器的排水管出口后面的涡旋.为更好地获得涡流发生器的相关流场特性，司乔瑞等[7]采用了接触式探针和PIV技术，对包含涡流发生器的导叶式离心泵进行了较系统的研究，发现涡流发生器可有效改善导叶内的流动特性.

然而，鲜有学者对水力学中涡流发生器本身的尾涡特性展开研究.鉴于此，在文献[8]的基础上,文中设计安装边长依次为2，3，4 cm的涡流发生器，采用大涡模拟与PIV测量相结合的方法，对叶片的安装角度、叶片高度和安装边长度及外界水流速度对尾涡特性的影响进行研究，为涡流发生器在水力学中的应用提供一定参考.

1 试验设备与方法

1.1 试验设备

试验平台主要由试验水槽、水泵、涡流发生器、水箱和粒子测速平台等组成，见图1，其中试验水槽为一个长2 500 mm，宽150 mm，高250 mm的长方体.水槽的出口设置一个蓄水装置，利用流量为0～8 000 L/h的变频水泵实现整个水槽水体的循环.

图1 试验系统示意图

为了使试验段处的流动更加均匀，水槽进口处依次设置钢丝球和3个不同直径的蜂窝板作为整流段，同时将水槽的出口设置抽拉式开口，呈矩形.水槽底面采用普通玻璃，两侧面采用透光性较好的超白玻璃.用厚度约1 mm的白铁皮制作各种尺寸的涡流发生器.试验过程中，用螺柱将涡流发生器固定在水槽底部.

粒子测速平台主要是由美国TSI公司的2D PIV- V3V系统和光学平台组成.该仪器2D的测量范围为700 mm×700 mm.当水体流动稳定后，示踪粒子完全跟随流场运动.采用双脉冲激光点亮粒子并用同步器连续拍摄2张粒子图像.依据激光跨帧延时计算出粒子图像的时间间隔Δt，TSI自带后处理软件可以分别计算出粒子的位移Δs，进而可以求解水体的流动速度.

1.2 试验方法

试验过程中，通过调整整流段、水槽高度等，使试验段产生连续均匀流，水流速度为0.07 m/s.图2为单叶片涡流发生器物理模型，其中涡流发生器叶片长度为L，叶片与来流方向的夹角计为β，水平方向上叶片位于水槽的中心位置.定义叶片顺时针旋转为正角度，反之则为负角度.沿水流方向，叶片距离进水口的距离为10L，与出水口的距离为30L，研究区域为40L×10L的二维平面.

图2 单叶片涡流发生器物理模型

试验在室温条件下进行，通过扭转安装螺柱调节涡流发生器与来流的夹角.单次试验测量完成后放空水槽中的水，更换涡流发生器.

2 数值计算

2.1 流场计算模型

试验段的均匀流速依次设定为0.02，0.03，0.04 m/s.根据端木玉等[9]对绕流问题的研究，低雷诺数时可以把三维的绕流问题简化为二维.

为突出涡流发生器的尾涡特性，建立连续性和不可压缩的N-S滤波方程，过滤尺度比较小的涡.由于被过滤掉的小涡可能对大涡产生影响特引入附加应力项[10-11].过滤后，得到大涡模拟的控制方程为

(1)

(2)

亚格子应力即为过滤掉的小尺度旋涡对大涡产生的附加值.为使方程(2)封闭，构造亚格子应力模式，选用最基本的 Smagorinsky 模式，即

(3)

(4)

2.2 网格划分及检验

应用Pointwise18进行网格划分.由于叶片附近及叶片尾流区流场变化较快且尾涡特征较复杂，需要自带拉伸功能的高质量网格进行划分.将靠近叶片的第一层网格设置为0.05 mm，拉伸的增长率设置为1.1.为提高计算效率，尽量减少远离涡流发生器和水槽壁面处的网格.

为验证网格密度与计算结果的关系，依次采用网格数为75万、150万和300万进行数值计算.随机抽取叶片前端面、叶片后端面和叶片后5 cm处截面的水体流动速度为研究对象，发现在相同工况下，叶片前端面处水体的流速依次为0.062，0.060，0.060 m/s；叶片后端面处水体的流速依次为0.029，0.024，0.024 m/s；叶片后5 cm处截面水体的流速依次为0.069，0.071，0.071 m/s.综合考虑计算性能和效果，选用总网格数150万进行计算，并对叶片表面网格的y+值进行检验，发现y+值均小于1，符合大涡模拟的要求.

2.3 边界条件及求解器设置

水槽入口边界条件设置为速度进口，出口边界条件设置为自由开放式出口.整个流道的下表面和涡流发生器叶片均设置为“wall”，流道的上表面设置为可自由滑移表面.为保证水体流动充分发展，将流道的左右2个表面均设置为对称边界.计算时选择水体温度为20 ℃，密度ρ=998.2 kg/m3.

采用有限体积法对控制方程进行离散，压力和速度耦合采用SIMPLE算法，时间项采用二阶隐式，压力项采用二阶迎风格式，对流项和扩散项采用二阶中心差分格式.首先选择k-ε模型进行稳定性分析，在获得比较合适稳定的初始流场后选择大涡模拟进行瞬态计算.k和ε的残差精度设置为10-5，其余残差设置为10-3，时间步长设置为0.02.

3 计算结果及分析

3.1 尾涡大小和间距

首先选用二维模型进行数值分析.采用涡量对尾涡大小进行描述，即

(5)

图3为叶片长度为2 cm、流速为0.02 m/s下不同安装角度时的涡量云图.

图3 叶片不同安装角度瞬时涡量云图

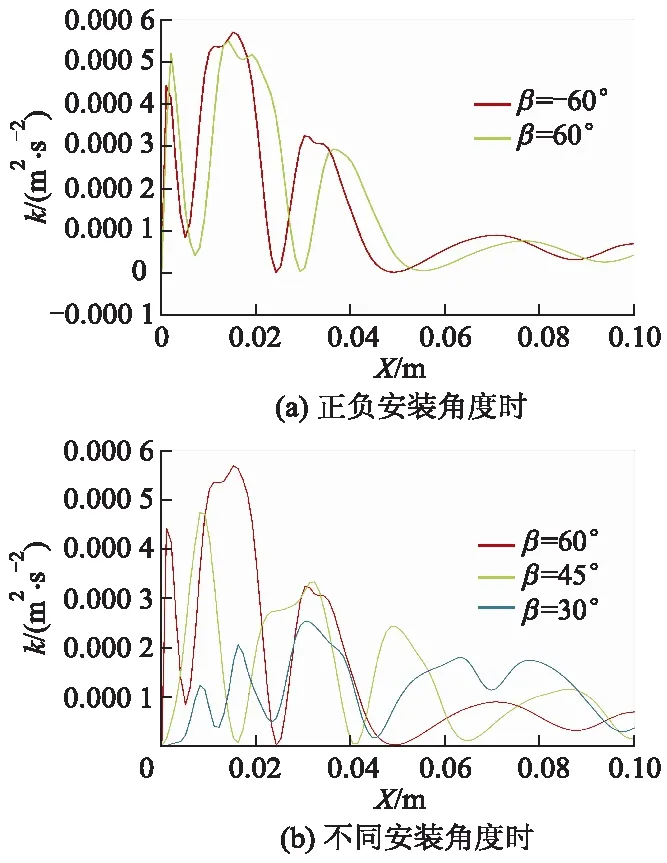
由图3可以看出：水体流过涡流发生器后，叶片两侧发生流体分离，进而在叶片后形成尾涡；安装角度±30°，±45°，±60°下在相同的区域内(-0.05

由图3还可以看出，随着涡流发生器安装倾斜角度增大，涡旋的强度逐渐增大，在±60°夹角时，涡心强度达到最大值7.0.将涡流发生器倾斜方向相同和相反的涡旋分别定义为同向涡和反向涡，同向涡与水流方向夹角小于反向涡旋与水流方向的夹角.随着涡旋与涡流发生器径向距离的增大，这些夹角先增大后逐渐缩小，直至与水流方向一致.随着安装角度绝对值的增大，水平方向上相邻一组涡旋间的距离逐渐缩短，而每组涡旋之间的距离逐渐增大.

图4为叶片长度2 cm、安装角度15°时不同流速下涡流发生器尾涡的分布情况，可以看出：在相同的区域内，尾涡中同向涡的强度随着流速增大而增大，并且增幅高于线性增大的幅度；每组涡旋中同向涡和反向涡的距离及相邻组涡旋之间的距离基本不变，相同区域内出现的尾涡组数相等；3种流速下尾涡与水流方向的夹角基本相同.

图4 不同流速下瞬时涡量云图

3.2 尾涡强度

尾涡强度是衡量尾涡的重要参数，可借助湍动能k值对尾涡强度进行描述，以研究流速、安装角度对尾涡强度的影响.定义湍动能k为

k=(u′2+v′2)/2,

(6)

式中：u′和v′分别为X和Y方向的速度脉动分量.

图5为叶片长度2 cm、流速0.02 m/s时不同安装角度下涡流发生器安装位置后中心线(0

图5 不同叶片安装角度时湍动能分布

图6为叶片安装角度为60°时不同速度以及不同叶片长度下的湍动能分布.

图6 速度和叶片长度对湍动能k的影响

由图6a可以看出：流速越大，湍动能越大，但是湍动能拐点的位置大致相同；随着流速的增大，雷诺数随之增大，湍流脉动速度也逐渐增大，即湍动能数值变大，表明尾涡强度也随之增大.由图6b可以看出：径向距离小于或等于叶片长度时，随着叶片长度的增大，湍动能值呈指数趋势增大；随着径向距离的增大，尾涡的湍动能值迅速衰减至0.