基于FRFT和相位差分算法的信号特征提取
2021-12-06黄治军
周 正,黄治军
(海军航空大学,山东烟台 264001)
基于分数阶傅里叶变换(Fractional Fourier Transform,FRFT)和相位差分算法的混合信号识别算法已被提出。FRFT 融合了时域信息和频域信息,被认为是1 种时频分析方法,可以用来分析和处理非平稳信号[1-3];相位差分算法则广泛应用于信号中存在的相位分量的检测[4-7],对于相位编码信号的识别具有重要的意义[8]。在已有文献中,该混合方法主要检测LFMBPSK[9]、LFM[10]、BPSK 信号[11]。但已有文献的仿真表明,该方法在低信噪比情况下的识别率较低。本文针对低信噪比条件下,识别率较低这一问题,给出了1种改进的新算法,并将Frank 信号引入到信号检测过程中,以提高改进算法的适用范围。
1 算法原理
1.1 FRFT概述
仿真实验中,由于计算机的处理是数据化的,因此,要将FRFT 进行数字化运算处理才能实现工程上的运用。本文采用Ozaktas 提出的经典的分解型算法[16-19]来实现FRFT。该算法很好地利用了FFT 的快速运算的特性。
考虑到主要讨论的是α≠nπ 的情况,FRFT 表达式可改写为:

1.2 相位差分算法及其表示方法概述
相位差分算法的基本思路是计算信号的瞬时自相关函数,通过混频等方式去除信号的载频分量,并为了计算方便,对信号的幅度进行归一化处理,提取出信号的相位分量[10-11],具体过程如下:
设接收到的信号为
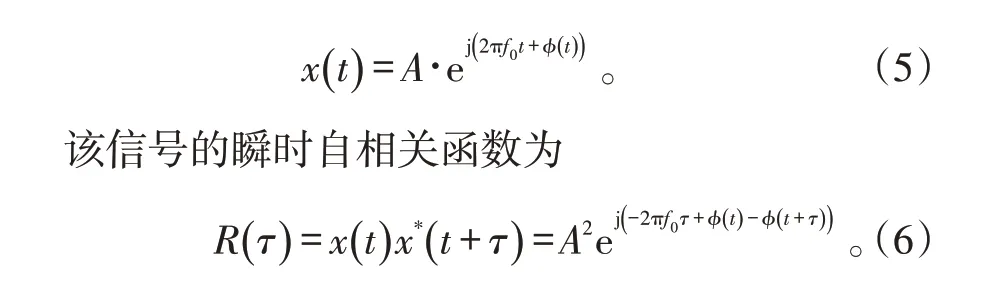
假设在频率估计准确的情况下,通过混频,结合信号幅度的归一化处理,可得到其中的相位分量:

由式(7)可知,若信号相位存在0、π 突变,则该信号的瞬时自相关函数取值为-1;若不存在相位突变,则信号的瞬时自相关函数为1。
因相位变化对噪声比较敏感,为减小噪声的影响,将对式(7)进行时域累加处理。该过程工程化表达式为:

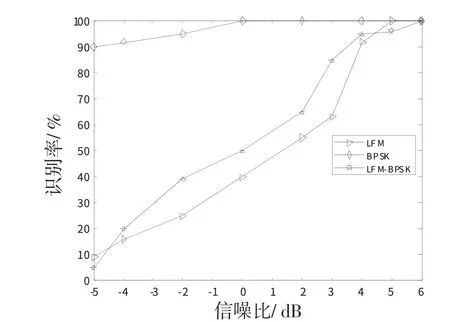
式(8)中,L是叠加次数,要求Lτ 该算法能够较好地检测出相位编码信号的存在。下面以13 位巴克码为例,仿真其相位差分结果,如图1所示。 图1 相位差分效果图Fig.1 Effect of phase difference 可以看出,峰值对应的时间就是发生相位突变的时刻。该方法能够有效检测出信号中的相位突变分量,这是区别LFM-BPSK和LFM信号的关键。 在本次识别的信号中,LFM、LFM-BPSK 信号由于存在调频分量,被认为调频类信号;BPSK、Frank编码信号仅存在相位调制,被认为调相类信号。下面对LFM、LFM-BPSK、Frank、BPSK4 种信号在改进算法中所用到的特征进行归纳。 LFM 信号在FRFT 域中具有良好的检测性能,然而LFM-BPSK 信号在FRFT 域中同样具有明显峰值,也较为容易检测,两者在FRFT域的图示如图2。 图2 调频类信号FRFT图Fig.2 FRFT diagram of frequency modulation signals 因此,在同时具有LFM-BPSK、LFM 信号的环境下,利用FRFT对LFM信号进行检测的效果较差。要借助相位差分算法对两者进行区别并检测。 对BPSK 信号的特征提取最为简单且较为可靠,其FRFT 峰值对应的阶数是1[7],且受噪声影响较小,理论分析上,其识别率最高,如图3。 图3 BPSK信号FRFT图Fig.3 FRFT diagram of BPSK signal 对Frank多相编码信号而言,该信号在FRFT域具有2个主峰,这是该信号的重要特征,如图4所示。 图4 Frank编码信号FRFT图Fig.4 FRFT diagram of Frank coded signal 文献[7]原算法流程,如图5。 图5 文献[7]原算法流程图Fig.5 Flowchart of the original algorithm in document 7 该算法运用数学工具FRFT 和相位差分算法(瞬时相位自相关累加)完成对LFM、BPSK、LFM-BPSK信号的识别。该算法利用的信号特征如下: 1)BPSK信号FRFT域的峰值对应的阶数为1; 2)相比于LFM 信号,LFM-BPSK 信号有相位编码分量,可利用相位差分算法进行识别。 该算法的信号识别率在信噪比低于0 时下降明显。 该算法存在以下几点不足, 1)相位差分算法对信号中的调频分量较为敏感,在调频斜率较大时,其相位编码分量中的相位突变数值太小,可忽略不计。在信号具有大的调频斜率时,相位差分算法性能较差,无法提取出相位突变分量。 2)该算法具有一定的应用局限性,无法检测多相编码信号等其他调制类型信号。 针对文献[7]原算法的不足之处,本文提出1种改进的算法,改进的识别流程如图6所示,具体操作流程如下。 图6 改进算法的流程图Fig.6 Flowchart of the improved algorithm 步骤1:通过现有硬件对脉冲的切割,粗略测量不同时刻的频率,可知信号是否存在调频斜率和初始频率,若存在,则认为该信号是调频类信号(LFM/LFM-BPSK )。若不存在,则认为信号是调相类信号( B PSK/Frank )。 步骤2:对于调频类信号,选择1个分选后的脉冲,通过测得的调频斜率和初始频率进行共轭运算,去除所选择的脉冲中的调频斜率和初始频率的相关分量;对处理后的信号进行相位差分运算,满足一定条件后,可认为信号存在相位编码分量,则认为信号复合调制信号LFM-BPSK(实际中也可能是其他相位编码形式,文章只讨论以13位巴克码为代表二相编码);若不满足上述的条件,则认为信号是单一调制的LFM信号。 步骤3:对于调相类信号,通过FRFT 可以区分开BPSK、Frank 信号。对分选后的信号中的单个脉冲进行FRFT 运算,并找出最高峰值所对应的P1,再找出第2 高峰值所对应的P2,记录下来。若P1的值为1,则说明该信号是BPSK 信号(实际上也可能是QPSK信号,在此不进行研究)。 步骤4:对不满足步骤3 要求的信号,另找1 个脉冲再次进行FRFT变换,同样找到最高峰和第2高峰各自对应的阶数P3、P4,判断是否同时满足2次变换的峰值高度差在容差范围内且P3=P1、P4=P2或者P3=P2、P4=P1(由于噪声的影响会产生较小偏差)。若满足上述条件,则认为信号是Frank信号。 从流程中可看出,相比于原算法,改进算法具有以下优势: 1)该算法通过引入现有硬件功能,着力降低LFM-BPSK信号在相位差分算法中调频分量的影响,从而增加相位差分算法的性能; 2)该算法引入了Frank 多相编码信号,增强了算法的适用性,并且通过2次FRFT检测Frank多相编码信号,增加了信号识别的正确率。 为了检验改进算法的有效性,下面对上述算法流程进行仿真检验。仿真选取上述4 种脉冲信号,分别是LFM、BPSK、LFM-BPSK、Frank 信号。其中,LFM信号起始频率为10 MHz ,调频斜率为上调频2×1012Hz/s,脉冲宽度为13 μs;BPSK 信号使用的是13位Barker码信号,码元宽度为1 μs,码长为13,脉冲宽度为13 μs;LFM-BPSK信号的码元宽度为1 μs,起始频率为10 MHz,调频斜率为上调频2×1012Hz/s,脉冲宽度为13 μs;Frank 多相编码信号的码元宽度为1 μs,信号的相数为10,即N=10,则码长为100,信号的脉冲宽度为100 μs。结合控制变量的方法,为便于仿真的进行,上述各个信号的幅度皆是1,FRFT 的步进阶数是0.01,总阶数为0 到2,采样频率是100 MHz。噪声选取高斯白噪声。 在信噪比为-5~6 dB 的环境下进行300 次蒙特卡洛实验,实验结果,如图7所示。 图7 改进算法识别率Fig.7 Recognition rate of the improved algorithm 图7给出了上述4种信号在该算法下各自的识别率。可以看出,二相编码信号的识别率在低信噪比条件下较高;线性调频信号在改进算法中的识别率好于原算法对应的识别率;Frank 多相编码信号(10 相)和LFM-BPSK 信号的识别率在低信噪比条件下并不理想,尤其是LFM-BPSK 信号,在信噪比小于-3 dB 的条件下,其识别率急剧恶化,实用价值降低。但相较于原算法,LFM-BPSK 信号和Frank 多相编码信号的识别率有大幅改善。 图8 给出了文献7 的相关仿真结果。结果表明,改进算法具有更高的识别率。这体现了改进算法的实用性和信号特征提取的可靠性。 图8 原算法的识别率Fig.8 Recognition rate of the original algorithm 本文在已有的FRFT和相位差分算法的混合算法的基础上,针对低信噪比下原算法信号识别率低的问题,给出了1 种改进的算法。改进算法通过改变调频类信号的相位差分法检测的方式增加信号识别率,并在检测过程中引入Frank 多相编码信号,扩大该算法的适用范围。仿真实验表明,改进算法的信号识别率高于原有算法的识别率。虽有改进,但缺点还是不可避免地较原有算法具有更大的运算负担,且没有包含对跳频、频率捷变等信号的检测,适用范围虽然有一定程度的扩大,但还是存在局限性。下一步重点研究在不影响此改进算法检测效果的前提下,如何降低算法的计算复杂度,如何进一步扩大该算法的适用范围。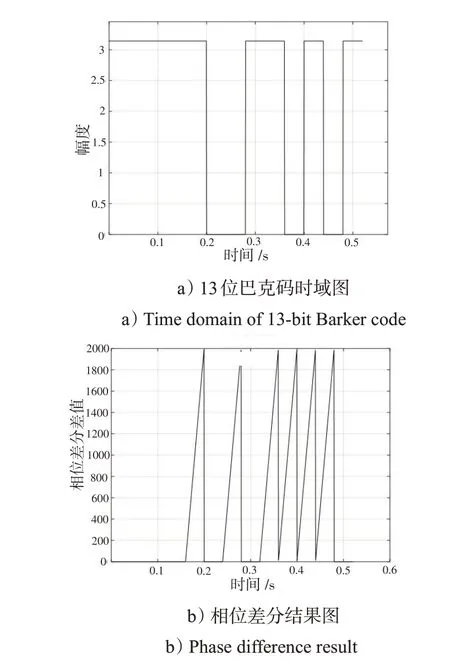
2 信号特征提取
2.1 调频类信号的特征提取

2.2 调相类信号的特征提取



3 信号识别算法流程
3.1 原算法流程及其识别率概述

3.2 改进算法流程

3.3 改进算法仿真验证

4 结论
