转化思想在初中数学解题中的有效应用
2021-12-03苏帅
苏帅

摘要:數学思想是初中数学学习的核心要素,也是促进学生思维能力提升的关键所在,其中,转化思想是一种非常重要的数学思想,也是重要的解题策略。在初中数学教学中,教师应注重转化思想的讲解,指导学生更好地解答相关数学难题,从而提高解题能力,助力学生获取新知和积极探寻解题思路,提升学习效果,为学生数学学习成绩的提升奠定坚实基础。
关键词:初中数学;转化思想;数学解题;难题;应用
中图分类号:G4 文献标识码:A
转化思想属于数学思想方法中的一种,指的是将一个数学问题由难化易、由繁化简,不仅是一种重要的解题思想,还是一种最基本的思维策略,更是一种有效的数学思维方式。在初中数学解题教学中,教师需高度重视转化思想的渗透,指导学生通过灵活自如的转化把陌生、复杂的难题变得熟悉、简单,并化抽象为直观、未知为已知,提高他们的解题能力[1]。
一、陌生转化成熟悉,降低数学题目难度系数
初中数学的学习过程是由一开始的陌生、浅层了解慢慢过渡至熟悉和深层了解,本身就是一个循序渐进的过程,为帮助学生更好的解答数学难题,可以应用转化思想,将陌生题目转化成熟悉题目,有效降低难度系数,使其轻松解题。如,在解二元一次方程组2y=x+4①,3x+y =5②时,由于学生是初次学习和接触二元一次方程组,当第一眼看到这样的题目时,会感觉到难度较大,如果直接采用消元法,他们可能无法顺利求解。这时教师可以引领学生了解有关方程其它方面的知识,他们可能想到一元一次方程,将会考虑怎么把二元一次方程转化成一元一次方程,由陌生化的难题转化成熟悉化的常规题目。比如,教师可提示学生把原方程进行变形,得到有关x 或者y 的只带有一个未知数的方程,对于①来说,可以转化成x=2y-4 或y=,而针对②而言,能够转化成x=或y = 5-3x,然后让他们把某个式子代入到另外一个方程当中,从而实现陌生向熟悉的转化,数学题目的难度自然下降,难点不攻自破。如此,在解答数学难题过程中,学生通过新知识向旧知识的转化解题思路变得更为清晰,让学生对难题不再惧怕,使其慢慢建立解题自信心,最终轻松解题。
二、复杂转化为简单,顺利找到解题的突破口
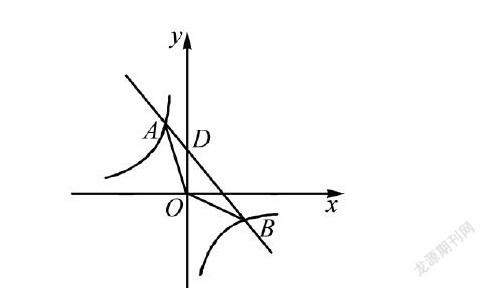
简化数学难题作为转化思想中最为常见和比较有效的一种解题方式。 初中数学教师应当教会学生当遇到比较复杂的难题时,先仔细研读与思考题干中给出的信息,再找到隐性条件,将复杂题目转化成简单题目,使其求出正确答案,让他们逐渐形成观察题目、挖掘细节的意识,学会从题目细节之处着手。如,已知一次函数y =-x + 2,反比例函数y =-8 /x,图像如下图所示,它们相交于A、B 两点,那么A、B两点的坐标分别是什么?
在本道题目中,涉及到一次函数和反比例函数两类函数,学生一定要找到这两个函数之间的关系,然后才可以顺利找到解题的突破口,他们要先分析题目中给出的已知条件,使其利用“图像相交于才A、B 两点”这一共同点,分析是否能把这两个函数转化成具体的方程组,再利用方程组解决问题,由此求出A、B 两点的坐标。此时,教师可组织学生以小组合作的方式解答难题,彼此分享与交流解法,深入研究这两个函数之间的关系,有的同学将会提出利用方程组,但是部分同学可能对方程组的解法不够熟练,他们在合作中快速解答方程组,即y = -x + 2①,y =-8/x②,解得x=-2,y =4,或x=4,y =-2,最终判断得出A点的坐标是(-2,4),B点的坐标是( 4,-2) 。
三、数形间相互转化,辅助学生快速解答难题
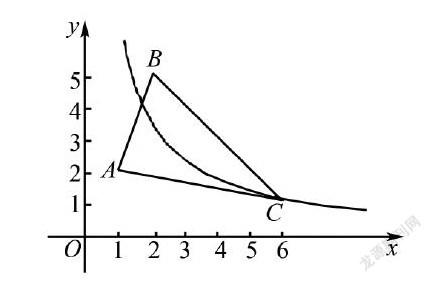
形与数转化是初中数学解题中应用率较高的转化方法。为使学生能够具体问题具体分析,通过形与数的灵活转化顺利、高效解题应注重为学生灌输相关理论,掌握形数转化的相关思路,如遇到方程问题可转化为函数图像交点问题等。另外,为使学生掌握这一重要的转化方法,应注重为学生讲解有难度的习题[2]。通过习题的讲解使学生掌握形数转化解题时的一些细节,在以后的应用中多加留心。如下图所示,△ABC 的三个顶点分别为A、B、C。若函数y = kx在第一象限内的图像与△ABC 有交点,求解k的取值范围为()。A.2≤k≤ ;B.6≤k≤10; C.2≤k≤6 ;D.2≤k≤
该题难度较大,准确找到形数转化的切入点是解题的关键。 根据所学的反比例函数知识可得当k>0时k 的值越大,越远离y轴。可知反比例函数经过A 点为其左边的临界,右边需要和直线BC 相交才能满足题意,此时可将其转化为函数交点问题。 当反比例函数经过A( 1,2) 解得k = 2; 由图可知B( 2,5) ,C( 6,1) ,解得直线BC 的函数表达式为y =-x + 7。其和反比例函数在第一象限有交点可将两者联立转化为方程有解的问题,即,kx=-x +7 有解,整理得到x2-7x + k = 0,即Δ= (-7)2-4k≥0,解得k≤。综上可知k的取值范围为2≤k≤,正确选项为A。
四、应用问题变更思想,灵活变换解题思路
在解题的过程中,如果一条思路行不通,学生就要将问题进行变更,寻找更加有效的解析思路。想要达成思维训练的目的,数学教师应当着重培养学生的数学基础,让学生牢记各种概念、定理。除此之外,教师要注重解题后的复习与巩固,让学生经常回顾做错的习题,纠正自己容易犯错的细节。这样才能帮助学生掌握转化思想的应用规律,避免在解题过程中出现错误。如下图所示:
如果在矩形ABCD 中,满足AD= 8,而点O 在直线AD 上不断运动,如果△OBC 为等腰三角形,并且满足这个条件的点O 只有三个,试求AB 的长度。许多学生在面对这类习题时会习惯性地按照等腰三角形的基本概念进行思考,即OB = OC,OB = BC,OC=BC。但在解析时,学生不知怎样满足“点O只有三个”这个条件。对此,可以适当变更问题。首先,在矩形ABCD 中,根据矩形的性质,当点O 为AD 中点时,OB = OC 必然满足题干条件。而关于OB=BC,OC=BC 的解析,可以从圆的半径入手解答。如以B、C 分别作为圆心,令BC 为半径进行画圆。如果BC 的长度小于AB,那么两个圆与直线AD 不会形成交点,不满足题意。若BC 等于AB,那么点O 刚好能与点A、点D 重合,在加上AD 的中点,正好满足“点O 只有3个”这个条件,此时BC= 8。若BC 长度大于AB,那么两个圆会在AD直线上分别形成两个交点,加上AD 中点,共有五个交点,不满足题意。但当两个圆都刚好经过AD 中点时,交点就变成了三个。此时,根据勾股定理,AB2 = OB2-AO2 = BC2 -AO2 =82-42,可以得出AB=。
五、结束语
总之,初中数学解题过程中,转化思想的应用普遍。为使学生认识到转化思想的重要性,自觉认真地学习这一重要思想,教学中既要注重传达相关的理论,又要结合具体例题应用转化思想,进一步深化其对转化思想的认识与理解,尤其注重设计相关的习题对学生进行训练,不断提高其对转化思想的应用水平。
参考文献
[1]王友楠.转化思想在初中数学解题中的妙用[J].中学生数理化(教与学),2020(07):92.
[2]竺利群.初中数学解题中的转化思想应用与体现分析[J].数学学习与研究,2020(03):113.
