小学生代数思维的特征、表现及培养

刘加霞

北京教育学院初等教育学院院长，教育心理学博士，教授，教育部国培专家库成员;提出“把握数学本质是一切教学法的根”“实证研究学生是有效教学的根本”“培训实质是改变与创新”等观点，以及“CARE伙伴式”校本研修模式;在《课程·教材·教法》《中国教育学刊》《中小学管理》《人民教育》《小学数学教师》《小学教学》等期刊发表论文百余篇，著作有《小学数学有效教学》《小学数学有效学习评价》《小学数学课堂教学设计》等。

小学生的认知特点决定其数学思维主要是算术思维，但教师在算术教学中应该并能够渗透代数思维已成共识。具体来说，就是让学生理解数学内容的结构与关系、洞察并把握数学本质，而不仅仅指向算出结果。为实现此目标，首先需要教师认识到算术内容蕴含着代数思想，且代数知识的浅层学习未必能培养代数思维;然后需要教师理解并掌握算术思维与代数思维的本质特征与行为表现，并在日常教学中有意识地渗透代数思维，帮助学生克服算术思维定式。

一、算术与代数思维的本质区别

综述相关文献可知，算术思维主要由程序性思维（procedural thinking）来刻画，体现于按照某种程序或步骤获得正确答案的过程。代数思维则由关系或结构（relation or structure）来描述，目的是明确内容结构，发现一般化的关系。代数思维主要体现在抽象与概括、归纳与推理、模式化与结构化等活动中，某种程度上不依赖直观操作。

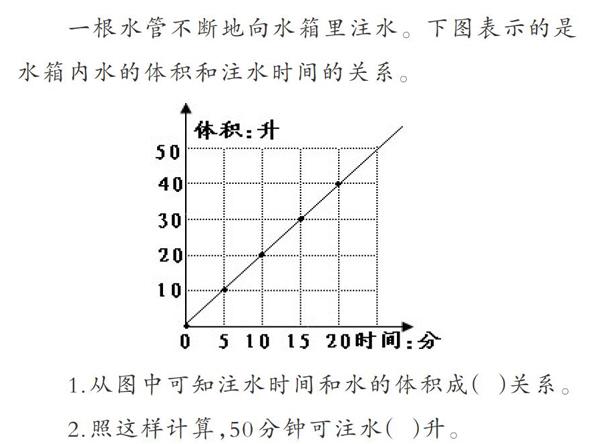
算术思维的对象主要是具体的数及其运算与静态分合;代数思维的对象则主要是代数式及其运算与动态变换。值得注意的是，常见的字母符号表达不是代数思维的唯一载体形式，图表和专门化的语言结构也能表达，如下题。

一根水管不断地向水箱里注水。下图表示的是水箱内水的体积和注水时间的关系。

1.从图中可知注水时间和水的体积成（ ）关系。

2.照这样计算，50分钟可注水（ ）升。

这个问题需要整体把握图象所表示的数量关系，利用比例解决。比例思维是典型的代数思维。

小学阶段所学的方程、正反比例等内容具有代数性质，是培养代数思维的重要载体。但这些内容在小学数学中的比重较少且目标要求较低，笔者对此不做重点分析。本文重点研究如何在算术教学中培养学生的代数思维。

基兰（Kieran）提出，从算术思维向代数思维的过渡需要满足以下条件：①聚焦关系，而不仅仅是数值运算;②聚焦运算和逆运算，及“设而不求”的思想;③聚焦对问题的表征及解决过程，而不只是答案;④聚焦字母符號，而不只是数字;⑤重新认识等号的意义。根据基兰的观点，结合小学数学教学经验，笔者系统地梳理出算术教学中学生的代数思维表现，并提出培养小学生代数思维的三条路径。

二、理解“=”的双重功能是形成代数思维之始

代数知识蕴含着代数思维，但学习代数知识并不等于培养代数思维。例如，计算[5x+3x]等于[8x]时主要是算术计算，还不是严格意义上的代数思维，因为学生计算时对“[x]”几乎“视而不见”。如何在这样的算术计算中发展学生的代数思维呢？第一步就是对“=”的双重认识：不仅表示“程序性计算的结果”，更表示“结构性的等量（价）关系”。

如果学生认为“=”表示的是要求计算左边算式的结果，其思维处于算术思维水平，具有程序性、操作性与过程性特征。处于算术思维水平的学生认为：计算结果总在“=”右边，是一个具体数值，如果是“算式”，则多数学生不会认可。他们见到算式“7+3”，往往条件反射般地写上“=10”，等号被理解成执行加法运算的标志，成为算式与具体数的“分隔符”。几乎不会有学生写“=8+2”“=9+1”等。算术教学应该打破这种思维定式，让学生认识到“=”所表示的不只是一个动态的计算过程，还表示左边算式与右边算式的“等量关系”，能认可等号右边的项不是具体数而是算式（含字母的代数式）。

代数思维具有关系性、对象性与概括性特征。无论“=”左右两边所出现的表达式如何复杂，具有代数思维的学生都能将等式看成一个整体（对象），甚至能对其进行数学操作，如恒等变形等。

对“=”的理解达不到代数思维水平，会导致学生出现这样一些错误。例如，将“3+4=（  ）+6”错填为“3+4=（7）+6=13”;将“8=（  ）÷（  ）”错填为“8=（2）÷（16）”（误认为“=”要求执行“从右向左”的除法计算）;脱式计算时出现结果正确但“表达过程”错误的现象;解决“苹果有5个，橘子是苹果的2倍还多4个，橘子有多少个”的问题时，错误地表达为“5×2=10+4=14”;错误地用“[4x=14+2=16=4]”的形式解方程等。这些现象从数学角度看是错误的，但从学生认知角度看却是“正确的”。教师要理解学生出错的合理性，有针对性地对比分析，强化学生对“=”表示等量关系的理解。

学生处于算术思维水平时，判断“=”成立要进行计算;具有代数思维时，则能够利用运算的性质、定律等解释等式成立的理由。如解释78-49+49=78的理由，学生能从算式结构思考，运用“准变量”来陈述。

三、用好“准变量”，培养学生概括归纳与代数推理能力

有研究认为，在算术教学中有效运用“准变量”这一概念能促进学生从代数视角看问题，把握问题结构及其蕴含的规律，培养学生的概括归纳与代数推理能力。

“准变量”是“一个或一组数字语句”，蕴含着一个潜在的数学关系。在这种关系中，不管它所包含的数字是什么，语句都是真的。例如，陈述78-49+49=78[是真语句]的理由。当学生不需要计算，直接通过观察算式的整体特点做出正确判断，得出“减去一个数，再加上这个数，不改变计算结果”时，就是在运用准变量进行代数推理。准变量可以是语句，也可以是代数表达式。例如前述语句在高水平代数思维下的表达为[a-b+b=a]。小学低年级不要求达到该水平，但要求用准变量进行计算或做算理解释。

准变量思维的对象可以是非字母符号的语句或关系式，它超越算术计算，利用算术中隐含的数量关系与运算性质识别并提取关键数字和关系性元素，对潜在的结构进行表达和转换。运用准变量算得结果或推理时的数学思维已经远离算术计算，其目的不是通过计算算出答案，而是将“等式”作为思考的对象。因此，有研究者称之为“无过程的对象化”。

例如，一年级学生计算9+6=？一般有数数法、拆分凑十法等。如果这些方法只是算出结果，有明确、具体的计算步骤和程序，那么这一过程主要是算术思维。如果教师引导学生继续思考“6有多种拆分，为什么只选择1和5”，整体观察多种拆分得出的算式特征，进而得出“第一个加数与‘几能凑出‘十，就把第二个加数拆出‘几”的规律，那就是在培养代数思维。教学中，有的学生用“平衡抵消凑十法”思考，即9+6=9+1+6-1=15，如其理由为“加上一个数再减去这个数，大小不改变”等，就是基于准变量的思考，有利于培养代数思维。如果学生口算71-24的过程是70-20-（4-1）=50-3=47，就发现了算式蕴含的结构和规律。基于此，口算的重要性显著地高于笔算。

澳大利亚学者提出的“有坏键的计算器”问题也非常有价值：一个计算器上的“5”键坏了，不用“5”键，如何用这个计算器计算525-257？有的学生用424+101-247-10=268，有的学生用636-368=268等。此外，探索并运用商不变性质、分数或比的性质以及其他规律解决问题时，以准变量作为桥梁，能促使学生从算术思维转向代数思维。

前述例子的共同特点是学生都将“算式”作为思维对象而不是数字运算。对算术问题进行“代数思考”，其所蕴含的等价、抵消与恒等变形等思想是重要的代数思想，为正式学习代数内容、形成代数思维搭建了脚手架。教师应该有意识地让学生直觉地、隐性地利用运算的性质与定律，即用好准变量求得算式结果或进行代数推理，引导学生关注算式或等式的结构与规律，为学生提供丰富的学习材料和解释、交流的机会。

四、列而不算，引导学生关注问题的结构与规律

不承认算式（代数式）表示结果，可以说是培养学生代数思维的最大阻碍。例如，苹果每千克8元，买a千克需要多少元？学生顺利列出8[×]a，但有很大一部分学生会无意识地继续写上“=”并试图算出结果，即使写出“8a”仍疑惑地问教师“到底花了多少元”，即使教师告之“就是8a元”，仍有很多学生表现出疑惑的表情。

其实不止小学生这样，很多成年人也不接受含有字母的算式能表示结果。教师应该让学生感受“8a”既体现出“单价[×]数量=总价”的数量关系，更是所花钱数的一般化表达。

要想突破该思维难点，教师在算术教学中就要重视列而不算、不急于算出具体答案、研究算式特点与规律等代数活动。例如，用“列而不算”法解决“握手问题”无须归纳得到公式[n（n-1）2]，更能培养学生的代数思维。先从简单数据开始，学生通过模拟握手、画图等方式得到算式。如，5个人握手次数是4+3+2+1，只列算式不计算结果，再来一人，因为其他人之间已经握过手，只需要在5人握手次数基础上再加5，即列式为5+4+3+2+1，依此类推，就可以得到握手次数的算式。也可以反过来提出问题：如果握手次数是10+9+8+7+6+5+4+3+2+1时，一共有多少人握手呢？通过算式结构而不是具体次数的更容易发现握手过程的“规律”，凸显列而不算的代数价值。

需要注意的是，思维对象中是否有字母符号并不是代数思维的本质特征。柯利斯（Colis）将字母在数学中的用法分为6类：①给字母赋值。如：若a+4=6，則[a=]（   ）。②忽略字母。字母被忽略或被视为无意义，如：当[a+b=6]时，求[a+b+2]的值。③把字母当成物体。如：5a+3a=（   ）a。④特定未知数。如：小明[a]岁，妈妈比小明大30岁，则妈妈[（a+30）]岁。⑤广义的数。字母是一种表示法，不只是代表一个数，如：若[a+b=6]，且[a

责任编辑  刘佳