拉格朗日乘数法在几何及偏微分方程中的应用

2021-12-03贾迪媛

贾迪媛，常雪

(南阳职业学院，河南南阳 474550)

1 拉格朗日乘数法在几何中的应用

解析几何中有关求解距离的问题，通常可以利用多元函数求解极值的方法来解决，下面使用拉格朗日乘数法来解决初中阶段的距离问题。之前推导点到平面的距离公式时，常常使用以下几种方法：(1)引进法式方程、离差，再求距离；(2)用平行平面法求距离；(3)用等体积法求距离。接下来利用拉格朗日乘数法来求出这个公式。

证：设P(a,b,c)为空间中任意一点，M(x,y,z)为平面Ax+By+Cz+D=0上的任意一点。该问题可以转化为求P、M两点间的最小距离。

已知P、M两点之间距离的平方为d2=(x-a)2+(y-b)2+(z-c)2，其约束条件为Ax+By+Cz+D=0，由拉格朗日乘数法可知，令L(x,y,z,λ)=(x-a)2+(y-b)2+(z-c)2+λ(Ax+By+Cz+D) 解方程组：

由(1)、(2)、(3)式得：

将结果代入(4)式整理得：

(2a-Aλ)A+(2b-Bλ)B+(2c-Cλ)C+2D=0 解得：

将此式分别带入(5)、(6)、(7)式中，得到(x,y,z)为唯一驻点：

高中时期已经学习了多种证明点到直线的距离公式的方法，如：定义法、函数法、不等式法、三角形法、参数方程法等。现在利用拉格朗日乘数法来证明点到直线的距离公式。

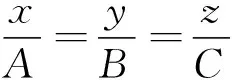
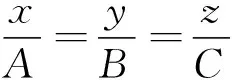
解得：

代入后两式整理得：

解得：

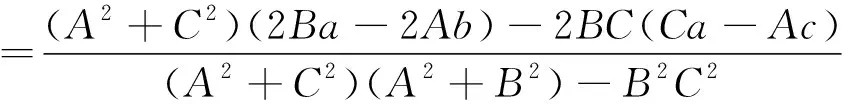
d2=(x-a)2+(y-b)2+(z-c)2

所以

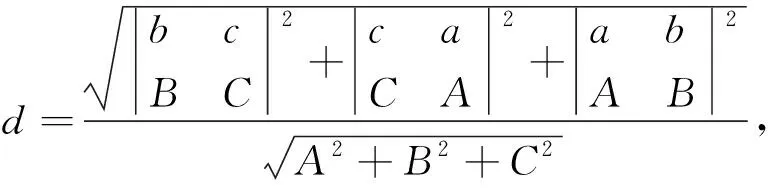
高等数学中常常利用数量积的几何意义、定义法、射影法、向量法、转化为面面距等方法来推导两异面直线的距离。现在利用拉格朗日乘数法来推导出两异面直线间的距离公式。

证：两直线矢量形式可表示成li:ri(t)=ri+tvi，其中ri=(xi,yi,zi)，vi=(mi,ni,pi)，i=1,2。由异面条件可得Δ=(v1×v2)2≠0。在两直线上分别取点r1(s)和点r2(s)，记r0=r1-r2，则两直线l1和l2的距离d的平方就是下面函数的最小值：

(1)

解得驻点为：

(2)

(3)

都成立。

拉格朗日乘数法作为一种基本的数学方法，能够将生活中的一些实际问题简化，在常见的距离公式和偏微分方程中得到了合理应用。