指数函数与对数函数核心考点综合演练

2021-12-03刘中亮

中学生数理化·高一版 2021年11期

关键词：奇函数指数函数业务员

■刘中亮

一、选择题

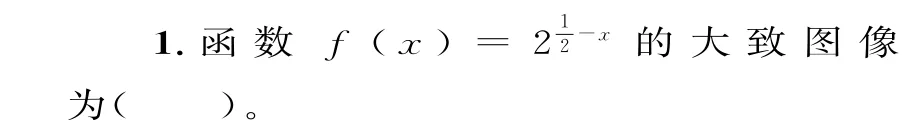
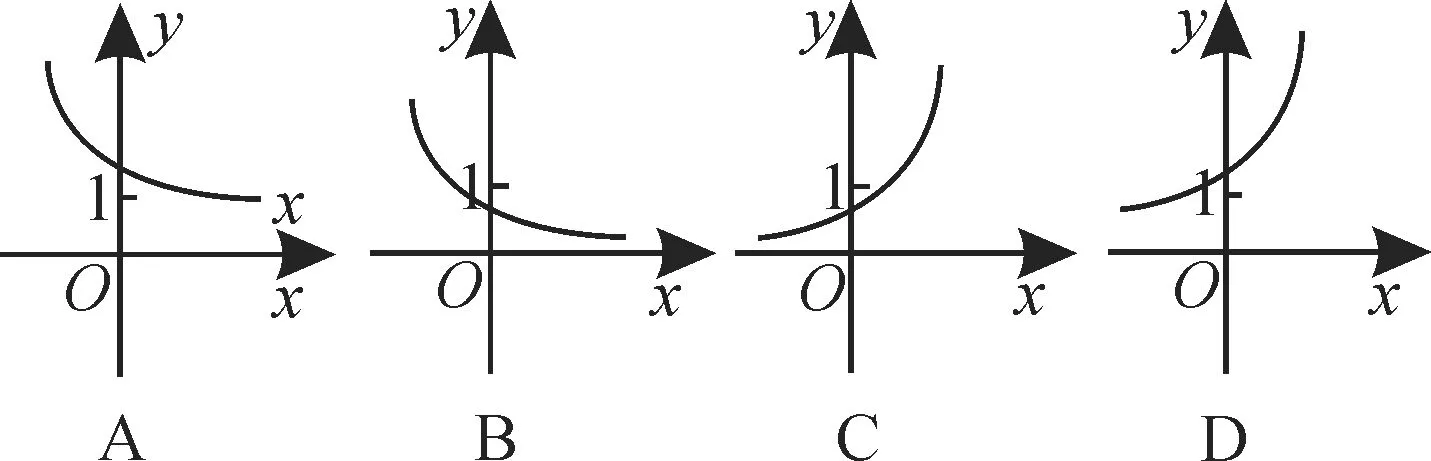
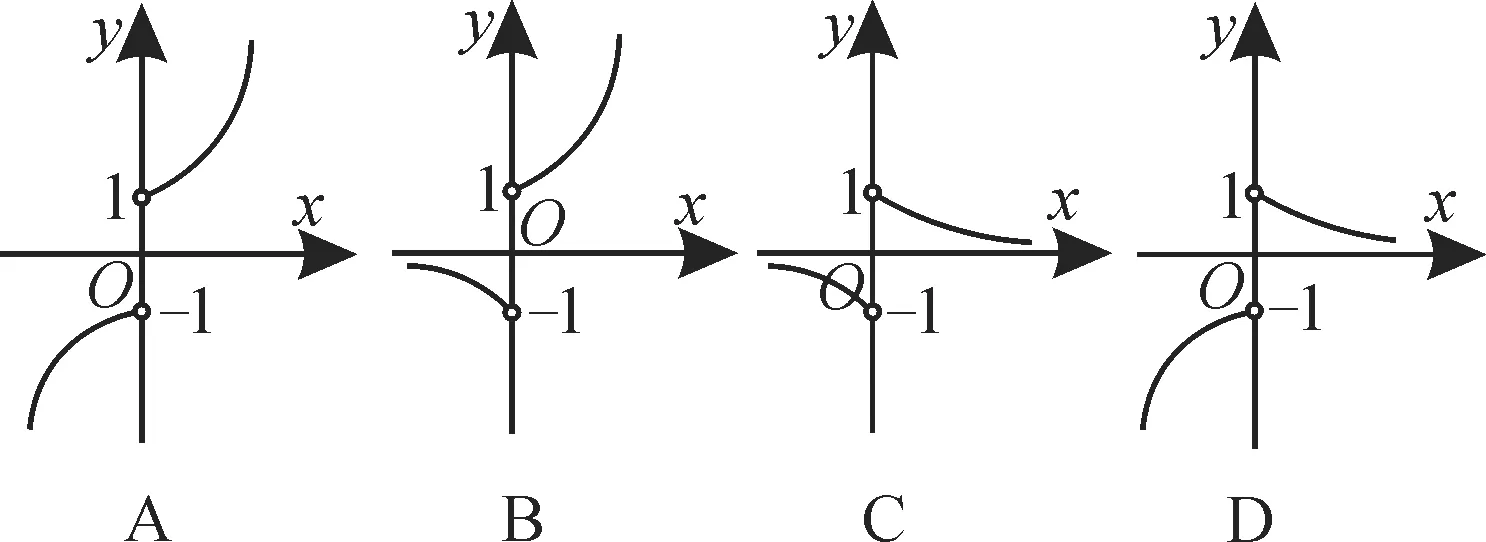
2.已知函数f(x)=(x-a)(x-b)(其中a>b)的图像如图1所示,则函数g(x)=ax+b的图像是( )。

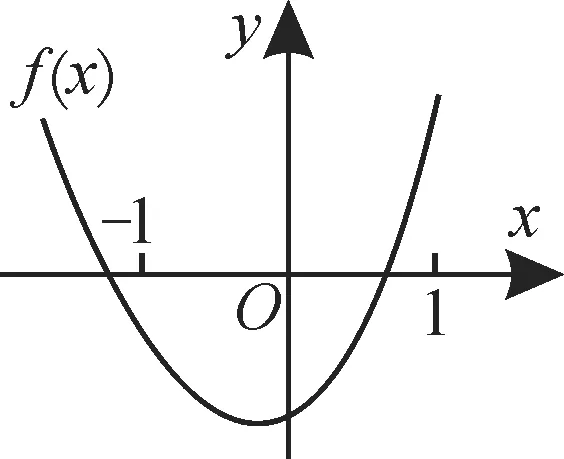
图1

3.已知x,y∈R,且2-x+3-y>2y+3x,则下列正确的式子是( )。

A.x-y>0 B.x+y<0

C.x-y<0 D.x+y>0

6.若a>1,b<-1,则函数y=ax+b的图像必不经过( )。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

7.设实数t满足2t+log2t=0,则( )。

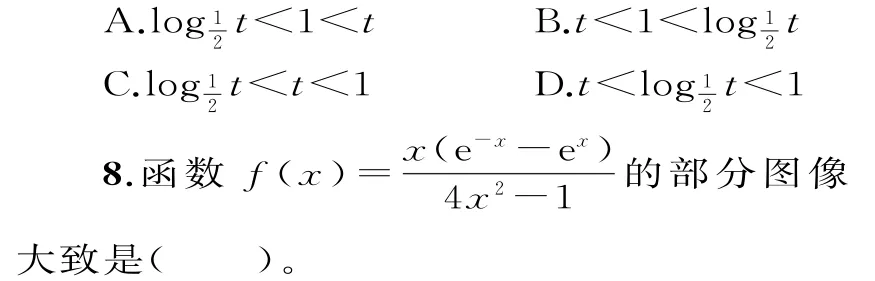
9.已知函数f(x)是定义在R 上的奇函数,当x≥0 时,f(x)=2x+2x-a,则f(-1)=( )。

A.3 B.-3

C.-2 D.-1

10.函数f(x)=x2-ln|x|的图像大致为( )。

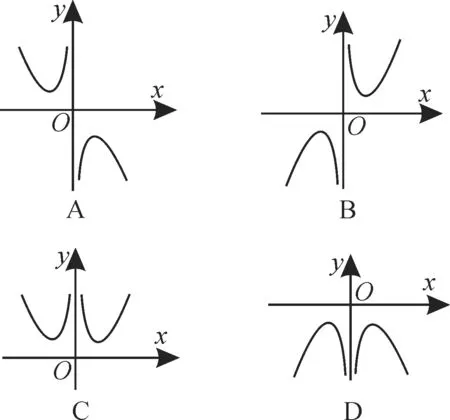
A.1 B.2 C.3 D.4

13.已知奇函数f(x)在R 上是增函数,g(x)=xf(x),若a=g(-log25.1),b=g(20.8),c=g(3),则a,b,c的大小关系为( )。

A.a

C.b

15.已知f(x)的一个零点x0∈(2,3),用二分法求精确度为0.01 的x0近似值时,判断各区间中点的函数值的符号最多需要的次数为( )。

A.6 B.7 C.8 D.9

16.某宣传部门网站为弘扬社会主义思想文化,开展了以核心价值观为主题的系列宣传活动,并以“社会主义核心价值观”作为关键词便于网民搜索。此后,该网站的点击量每月都比上月增长50%,那么第五个月的点击量和第一个月相比,增长了( )。

A.2倍以上,但不超过3倍

B.3倍以上,但不超过4倍

C.4倍以上,但不超过5倍

D.5倍以上,但不超过6倍

17.已知函数y=ax(a>0且a≠1)在区间[1,2]上的最大值与最小值之和为6,若函数f(x)=ax+logax+b在区间(1,2)上有零点,则实数b的取值范围为( )。

A.(-∞,-5) B.(-5,-2)

C.(2,5) D.(2,+∞)

18.(多选题)已知函数f(x)=ex-e-x,g(x)=ex+e-x,则以下结论错误的是( )。

二、填空题

三、解答题

(1)求实数a,b的值。

(2)判断f(x)在(-∞,+∞)上的单调性并证明。

(3)若f(k·3x)+f(3x-9x+2)>0对任意x≥1恒成立,求k的取值范围。

26.设函数f(x)=lg[(m2-3m+2)x2+2(m-1)x+5]。

(1)如果函数f(x)的定义域为R,求实数m的取值范围。

(2)如果函数f(x)的值域为R,求实数m的取值范围。

27.某公司为了激励业务员的积极性,对业绩在60万元到200 万元的业务员进行奖励,奖励方案遵循以下原则:奖金y(单位:万元)随着业绩值x(单位:万元)的增加而增加,且奖金不低于1.5万元,同时奖金不超过业绩值的5%,不低于业绩值的2%。

(1)若某业务员的业绩为100万元,核定可得3万元奖金,试分析函数y=lgx+kx+1(k为常数)是否为符合公司要求的奖励函数模型,并说明原因。(lg2≈0.3,lg3≈0.48)

(1)证明:函数在区间(0,2)内有实数解。

(2)利用二分法,取中点三次,指出方程f(x)=0(x∈[0,2])的实数解x0在哪个较小的区间内。

一、选择题

2.提示:由函数f(x)=(x-a)(x-b)(其中a>b)的图像可知0

3.提示:若x+y<0,则x<-y,y<-x。因为指数函数y=2x,y=3x在R 上单调递增,所以3x<3-y,2y<2-x。两式相加得3x+2y<2-x+3-y,适合题意,因此x+y<0满足条件。应选B。

5.提示:当x>0时,可得y=ax(a>1),当x<0时,可得y=-ax(a>1)。由此可知此函数的图像适合选项B。应选B。

6.提示:y=ax+b的图像是由y=ax(a>1)的图像向下平移|b|个单位得到的。应选B。

9.提示:由f(x)是定义在R 上的奇函数,且当x≥0 时,f(x)=2x+2x-a,可得f(0)=1-a=0,所以a=1。由此可得f(1)=4-a=3,则f(-1)=-f(1)=-3。应选B。

10.提示:此函数的定义域为x≠0。由f(-x)=(-x)2-ln|-x|=x2-ln|x|=f(x),可得f(x)为偶函数,排除A,B。由f(1)=1-ln|1|=1>0,排除D。应选C。

17.提示:由题意知a2+a=6,解得a=2或a=-3(舍去),所以f(x)=2x+log2x+b。由指数函数与对数函数的性质知f(x)为增函数。要使函数f(x)在区间(1,2)上有零点,则f(1)=2+b<0且f(2)=22+1+b>0,解得-5

二、填空题

三、解答题

27.提示:(1)对于函数y=lgx+kx+1(k为常数),当x=100 时,y=3,代入解得k=0,所以y=lgx+1。当x∈[60,200]时,y=lgx+1 是增函数,但当x=200 时,y=lg200+1=lg2+lg100+1≈3.3<200×2%,即奖金不低于业绩的2%不成立,故该模型不符合要求。