函数零点问题“大盘点”

■杨瑞强

函数的零点问题不仅是“零点存在性定理”的应用,而且综合了函数性质、数形结合、分类讨论等多方面知识,是高考命题的主要内容之一。一个复杂函数的零点(从函数视角认识)可以等价转化为简洁方程的实根(从方程视角认识),也可以等价转化为两个规范函数图像交点的横坐标(从图像视角认识)。

一、函数零点所在区间的判断问题

例1 函数f(x)=log3x+x-2的零点所在的区间为( )。

A.(0,1) B.(1,2)

C.(2,3) D.(3,4)

解:(定理法)函数f(x)=log3x+x-2的定义域为(0,+∞),且在(0,+∞)上单调递增,其图像是一条连续曲线。由题意知

f(1)=-1<0,f(2)=log32>0,f(3)=2>0,根据零点存在性定理可知,函数f(x)有唯一零点,且零点在区间(1,2)内。应选B。

(图像法)函数f(x)的零点所在的区间可转化为函数g(x)=log3x与h(x)=-x+2图像交点的横坐标所在的区间。作出两个函数的图像,如图1所示。

由图可知,函数f(x)的零点所在的区间为(1,2)。应选B。

评析:判断函数零点所在区间通常有两种方法:①定理法,适用于容易判断区间的端点值所对应的函数值的正负;②图像法,适用于容易画出图像的函数。

二、判断函数零点的个数问题

A.3 B.2

C.1 D.0

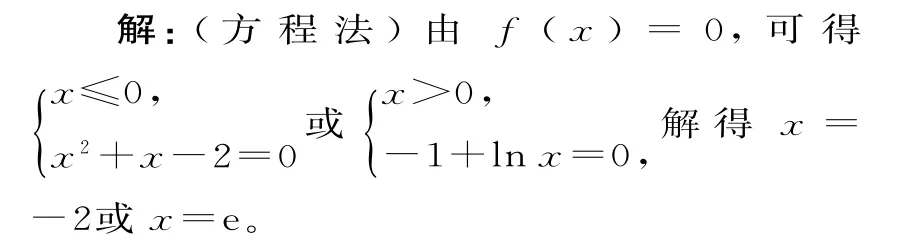
故函数f(x)共有2个零点。应选B。

(图像法):画出函数f(x)的图像,如图2所示。

图2

由图可知,函数f(x)共有2个零点。应选B。

评析:判断函数零点个数的三种方法:①方程法,令f(x)=0,如果能求出解,则有几个解就有几个零点;②定理法,函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,结合函数的图像与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有几个零点;③图像法,画出对应的两个函数图像,其交点的横坐标有几个不同的值,就有几个不同的零点。

三、根据函数零点个数求参数的问题

(2)函数g(x)=f(x)+x+a存在2个零点,即关于x的方程f(x)=-x-a有2个不同的实根,即函数f(x)的图像与直线y=-x-a有2 个交点。作出直线y=-x-a与函数f(x)的图像,如图3所示。

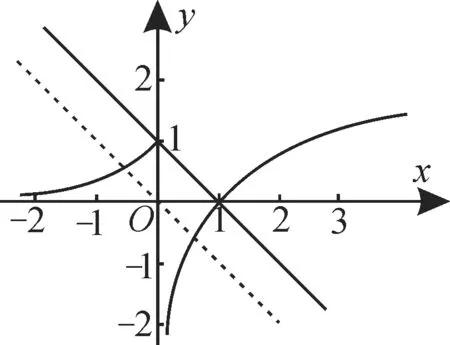
图3

由图可知,要使直线y=-x-a与函数f(x)的图像有2 个交点,需满足-a≤1,解得a≥-1,即a∈[-1,+∞)。

评析:利用函数零点个数求参数的三种方法:①直接法,根据题设条件构建关于参数的不等式(组),解出即可;②分离参数法,先将参数分离,然后将原问题转化成求函数的值域问题;③数形结合法,画出两个对应函数的图像,结合函数的单调性、周期性、奇偶性等性质求解。

四、根据函数零点所在区间求参数的问题

评析:根据函数零点所在的区间求参数的两种方法:一是转化成方程根的分布问题,这时需要考虑四个方面,即①开口方向,②所给点的正负,③判别式Δ的正负,④对称轴;二是转化成方程有解问题,进而转化为函数的值域问题。

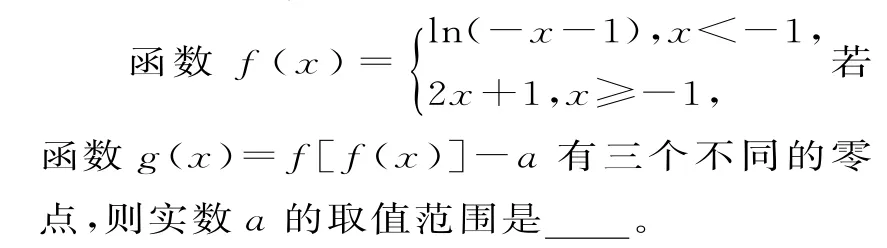
提示:令t=f(x)。由f[f(x)]-a=0,可得a=f(t),画出函数y=a与y=f(t)的图像(如图4)。

图4

当a≥-1时,y=a与y=f(t)的图像有两个交点(当a<-1时,y=a与y=f(t)只有一个交点,不合题意)。

设交点的横坐标为t1,t2(不妨设t2>t1),则t1<-1,t2≥-1。当t1<-1时,t1=f(x)有一解;当t2≥-1 时,t2=f(x)有两解。综上可知,当a≥-1 时,函数g(x)=f[f(x)]-a有三个不同的零点。故a∈[-1,+∞)。