全国名校必修5综合测试卷(A 卷)答案与提示
2021-12-03
中学生数理化(高中版.高二数学) 2021年11期
一、选择题
1.B 2.D 3.B 4.C 5.B 6.A 7.D 8.A 9.D

11.B
12.C 提示:延长CG交AB于D,如图1所示。

图1
因为G为△ABC的重心,所以D为AB中点且CD=3DG。

二、填空题
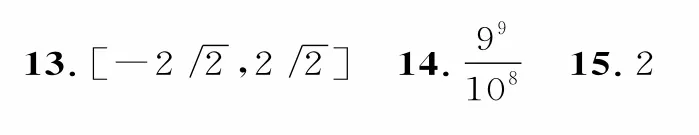
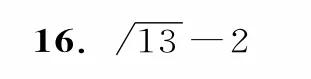
三、解答题
17.(1)由正弦定理得,sinC-sinB=sinAcosB-sinBcosA。
因为C=π-(A+B),所以sin(A+B)-sinB=sinAcosB-sinBcosA。
则sinAcosB+sinBcosA-sinB=sinAcosB-sinBcosA,2sinBcosA-sinB=0。

18.(1)如图2,结合题意画出图像。
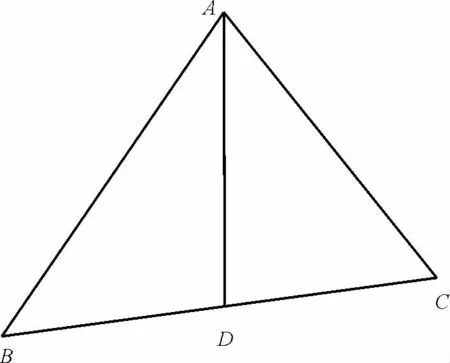
图2
因为AD是∠BAC的角平分线,所以∠DAB=∠DAC。


19.(1)当a=时,不等式f(x)>0可化为x2-3x+2>0。
由x2-3x+2=0,解得x=1,x=2。
因为抛物线f(x)=x2-3x+2 开口向上,且其两个零点为x1=1,x2=2,所以不等式f(x)>0的解集为(-∞,1)∪(2,+∞)。
(2)对于二次函数f(x)=x2-2(a+1)·x+4a,其对应的二次方程x2-2(a+1)x+4a=0的判别式Δ=4(a+1)2-16a=4(a-1)2≥0,其两根为x1=2,x2=2a。
当2a>2,即a>1 时,不等式f(x)<0的解集为(2,2a);
当2a=2,即a=1 时,不等式f(x)<0的解集为∅;
当2a<2,即a<1 时,不等式f(x)<0的解集为(2a,2)。
综上,当a>1时,不等式f(x)<0的解集为(2,2a);
当a=1时,不等式无解;
当a<1时,不等式f(x)<0 的解集为(2a,2)。


