浅埋小净距隧道爆破损伤探测及数值模拟分析*

2021-12-03刘闽龙陈士海揭海荣

爆炸与冲击 2021年11期

刘闽龙，陈士海，孙杰，何方，揭海荣

（1. 华侨大学土木工程学院, 福建厦门 361021；2. 济南城建集团有限公司, 山东济南 250031；3. 中铁二十四局集团福建铁路建设有限公司, 福建福州 350013）

在采用钻爆法开挖时，爆炸产生的应力波除了用于破坏岩石介质形成隧道外，不可避免会对围岩产生一定损伤。而围岩作为小净距隧道设计、施工的关键部位，对开挖的稳定性和支护结构参数的选取起着重要作用[1]。因此，爆炸对围岩造成的损伤是工程中重点关注的问题。

对爆破引起的岩体损伤已进行了大量研究，在损伤模型方面，Grady 等[2]和Taylor 等[3]率先提出了一些适用于岩石爆破的损伤力学模型，为后续研究提供了基础。陈俊桦等[4]建立了考虑初始损伤的弹塑性爆破损伤本构模型及提出了用于评价围岩受爆破影响的损伤判据；汪杰等[5]综合考虑岩体结构效应与荷载耦合作用，建立了节理岩体损伤演化模型及损伤本构模型；欧雪峰等[6]采用分离式霍普金森压杆探究了动态加载条件下层状板岩的各向异性行为，利用元件组合模型理论，建立了考虑宏观层理影响的层状岩体动态损伤本构模型。

在实际工程应用中，通常采用岩体的声波实验来评定爆炸荷载对岩体造成的损伤程度[7-9]。但现场的岩体声波测试实验过程较繁琐、操作不便，且这种事后的检测方法不利于爆破开挖中对于保留岩体损伤的主动控制。随着数值计算软件的不断发展，一些学者开始结合数值模拟来研究岩体的爆破损伤。Tang 等[10]采用累计拉应变和极限应变的比例关系来反映岩体的损伤程度，开发了用于研究岩体断裂破坏过程的RFPA 软件；Ma 等[11]将Johnson-Holmquist 模型嵌入LS-DYNA，研究了爆破裂纹扩展的影响因素，并对爆破损伤控制提出了建议；胡英国等[12]基于FORTRAN 和LS-DYNA 自定义接口，根据具体的工程实例，对5 种爆破损伤模型计算的精确性进行了对比计算和验证；曹峰等[13]通过Holmquist-Johnson-Cook (HJC)本构模型引入损伤变量，来研究在循环荷载作用下小净距隧道保留岩体的累积损伤演化过程；杨栋等[14]采用三维有限差分软件FLAC3D讨论了爆破荷载和地应力动态卸荷复合作用下隧道围岩损伤分布；李新平等[15]结合现场爆破振动测试和数值模拟以爆炸应力波作用下岩石内的有效应力确定了地下厂房爆破的损伤范围。谢福君等[16]根据提出的冲击荷载加载条件下的岩石压、拉统计损伤本构模型和冲击损伤判据模型分别进行爆破损伤数值模拟，并将数值计算结果和现场实测结果进行对比。

本文中，以济南顺河快速路南延工程浅埋暗挖段为依托，借助LS-DYNA 软件的二次开发功能将正交各向异性动态损伤本构用于爆破损伤模拟，探究各向异性条件下爆破荷载对隧道围岩的损伤效应；同时根据现场的围岩声波探测来评价岩体的爆破损伤程度，并与模拟的结果进行比较；以期研究成果可以为小净距隧道爆破开挖和岩体损伤控制提供参考依据。

1 工程概况

济南市顺河快速路南延建设工程，是构建济南市快速路路网骨架的重要组成部分，承担着主城区对外进出交通的快速集散任务，同时承担重要的公共交通走廊功能。地下道路工程暗挖段采用小净距隧道的结构形式，左、右线最小净距为南端洞口5 m，采用钻爆法施工。南口暗挖段起止里程K1+656.245至K3+125.101，顶板埋深为3.0～13.3 m，底板埋深为12.0～22.3 m。小净距段隧道设计断面，如图1 所示。

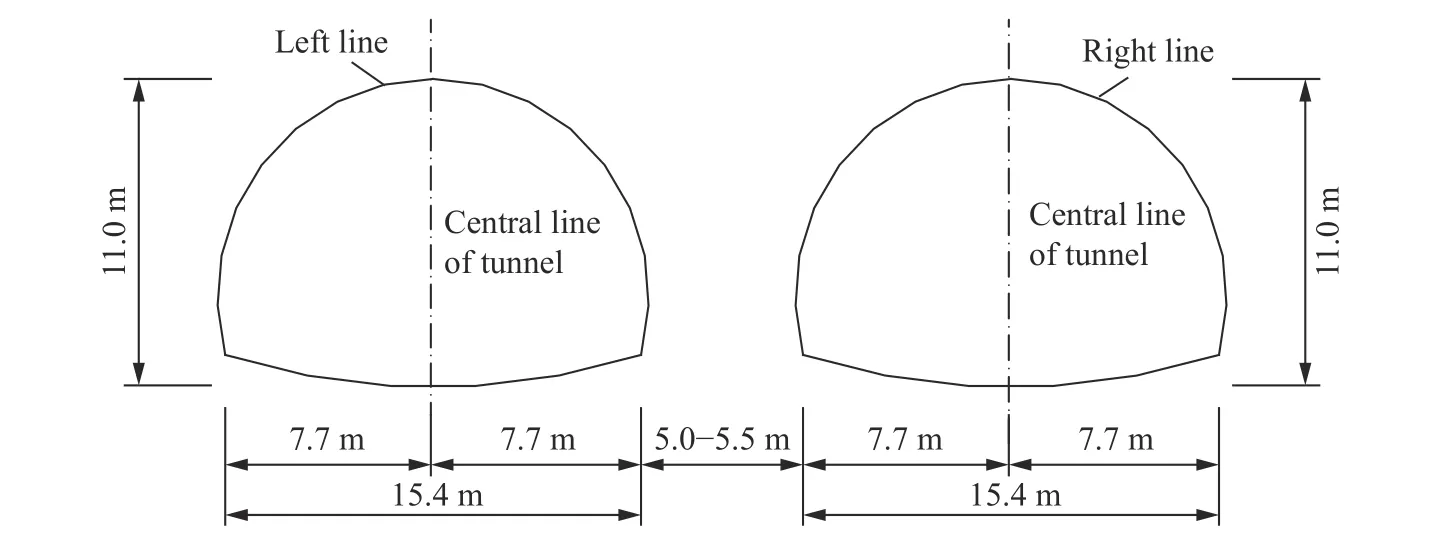
图1 小净距隧道设计断面Fig. 1 Designed cross-sections of neighborhood tunnels with small clear spacing

2 隧道爆破动态损伤数值模拟

2.1 岩石类材料正交各向异性动态损伤本构及应用

数值模拟是分析岩体爆破损伤行为的有效工具，但岩石类材料在爆破作用下具有明显各向异性的特征[17]。针对目前主流的数值模拟软件中对岩土体材料模型和结构模型都偏于简化，通常假定岩石为各向同性损伤材料，但在地质情况复杂、涉及到大量高应力的情况下，难以准确模拟出实际工况。故本文通过建立岩石类材料正交各向异性动态损伤本构，借助LS-DYNA 的二次开发功能将建立的损伤本构编译成动力有限元程序，对小净距隧道爆破损伤进行模拟计算。损伤本构的建立过程如下。

2.1.1 应变率效应

在动荷载作用下，岩石材料的力学响应和特性会发生变化，一般采用动态增长因子（dynamic increase factor，DIF，β）来考虑应变率效应，β 一般通过实验来确定[18]：

2.1.2 动态损伤损伤演化

首先，根据Sidoroff 能量等价原理[19]，受损材料与虚构无损材料的弹性余能密度相同，即：

然后，采用Mazars 损伤模型[19]描述主轴方向的损伤变量Di（i=1,2,3），则对于单轴拉伸情况：

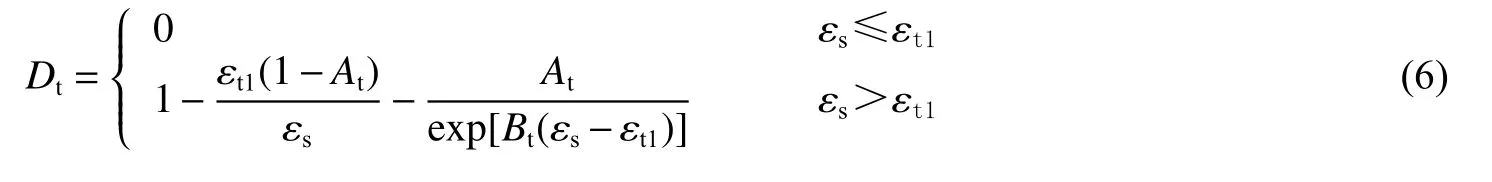
对于单轴压缩情况：

2.1.3 破坏屈服准则

采用Hoffman 正交各向异性体破坏准则[20]：

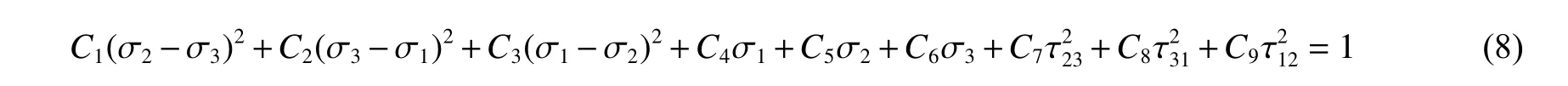
式中：σ1、σ2、σ3为材料3 个正交主方向上的应力；τ23、τ31、τ12为剪应力；C1、C2、···、C9为9 个基本强度参数，由3 个主方向的抗压强度、抗拉强度和3 个主平面内的剪切强度决定，具体表达式见文献[20]。

2.1.4 LS-DYNA 的二次开发

要想对前述建立的岩石类材料动态损伤本构模型进行计算，必须借助有限元分析软件。由于涉及用户自定义的本构模型，因此采用具备二次开发功能的通用显式非线性有限元分析程序LS-DYNA。其目前材料库有300 多种材料模型，能满足大多数的工程需要。但有时针对某一领域的具体应用，需要用到特殊的材料模式。LS-DYNA 通过开放程序内核，让用户根据实际问题开发相应的模块来增强主程序的功能。

LS-DYNA 的二次开发，实际上就是要修改原有的可执行文件，在其中加入自己的程序。目前，LSDYNA 开发商给用户提供的二次开发方式过程为：根据自己建立的材料模型编译相应的用户子程序代码，然后嵌入到主程序目标文件中的相应位置，再编译生成新的含有用户子程序的LS-DYNA 执行程序用于数值计算。

2.2 数值模型及参数

2.2.1 数值模型的建立

虽然在爆破工程上通常采用预裂或光面爆破技术，但事实上无论采用何种爆破技术都不可避免地对保留的岩体产生不同程度的损伤，造成围岩的力学性能劣化，承载能力下降[21]。根据掌子面上炮孔的布置规律，相邻周边孔的间距通常在0.5～1.0 m，而周边孔距隧道开挖轮廓线通常在0.1～0.2 m，因此在隧道爆破开挖时，爆破造成的围岩损伤主要来自邻近炮孔即周边孔的爆破作用。为简化模型，通过建立单个炮孔，来模拟周边孔爆破后形成的损伤范围，从而评判对围岩造成的损伤情况。为减少计算量，根据对称性建立1/4 模型如图2 所示，模型的净宽边界几何尺寸为2.5 m×2.5 m×3.0 m (X×Y×Z)，模型右下角为1/4 炮孔如图2(b)所示，炮孔半径为0.02 m，孔深为1.4 m，炮孔网格尺寸小于0.7 cm，在对称面上施加法向位移约束。

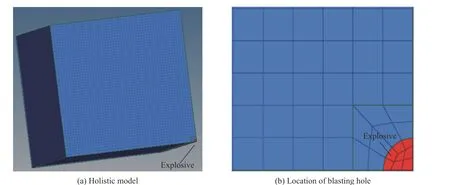
图2 数值计算模型及网格划分Fig. 2 Numerical model and meshing

2.2.2 材料参数

爆破数值模拟采用流固耦合算法，炸药采用MAT_HIGH_EXPLOSIVE_BURN 材料模型定义，炸药的爆炸过程采用JWL 状态方程进行模拟，其状态方程为[13]：

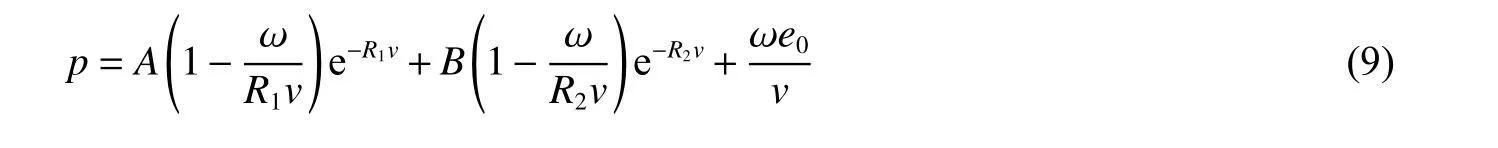
式中：A、B为材料常数；R1、R2、ω 为状态方程的常数；v为相对体积；e0为初始比内能。

炸药材料及状态方程参数见表1。

表1 炸药材料及状态方程参数Table 1 Explosive material and parameters of the equation of state

根据勘察报告及隧道设计参数建议，岩石材料所用物理力学参数见表2。损伤演化采用Mazars 损伤模型[19]，损伤演化方程所用参数中常数At、按取值范围选取，拉伸和压缩时极限损伤对应的极限应变值通过岩石强度计算得出，详细参数见表3。

表2 岩石材料物理力学参数Table 2 Physico-mechanical parameters of rock material

表3 损伤演化方程中的参数Table 3 Parameters of the damage evolution equation

2.3 数值计算结果与分析

图3 为爆破作用下岩石损伤演化趋于稳定后形成的损伤云图。对于岩体在爆破作用下的损伤判别，严格意义上，损伤因子D＞0 即表示岩体受到了损伤。图4 中黑色虚线为根据数值模型的计算结果得到爆破损伤的影响范围，假定损伤水平半径r为装药几何中心至损伤部位的水平距离，损伤深度h为炮孔顶部水平面至损伤部位的距离，可以看出此次爆破造成的最大损伤水平影响半径为0.58 m，最大损伤影响深度为1.88 m。同时考虑到爆破损伤对岩体产生的影响，通常以岩体损伤破坏阈值Dcr= 0.19，作为判定岩体是否破坏的依据[22]，则根据Dcr= 0.19 即可确定岩体的损伤破坏范围如图4 中红色虚线所示，岩体破坏水平半径为0.14 m，破坏深度为1.70m。从数值模拟结果可以看出，为尽量减小爆破对围岩的损伤，根据岩体破坏水平半径，周边孔距开挖轮廓线的距离应当大于0.14 m。

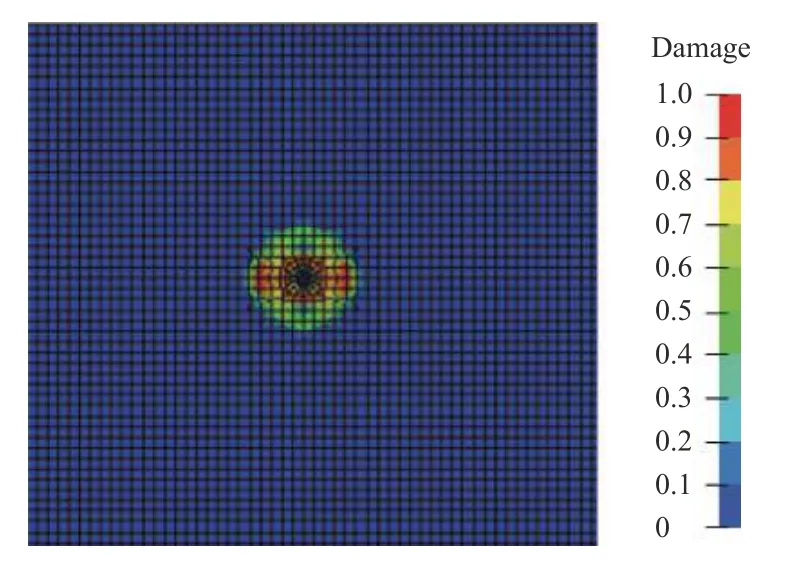
图3 炮孔周围爆破损伤范围Fig. 3 Blasting damage range around the blasting hole

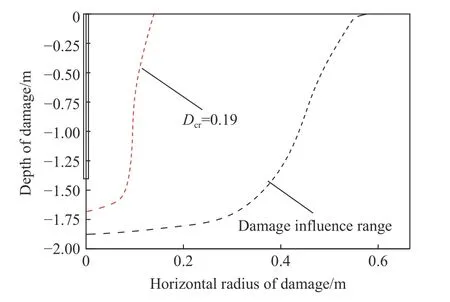
图4 爆破损伤范围Fig. 4 Range of blasting damage

3 现场围岩损伤探测

3.1 现场声波探测孔布置

在隧道南口桩号K2+947 中夹岩及隧道两边侧墙布置6 个探测孔如图5 所示，探测孔直径为0.04 m，孔深度为2 m，3 个探测部位位于同一水平面上，两孔间距选取为1.2 m。为防止测点布置过高，在下台阶开挖后难以探测，各探孔均沿隧道纵向布置在离隧道底板1.5 m 高的下台阶左右导坑的边墙上。

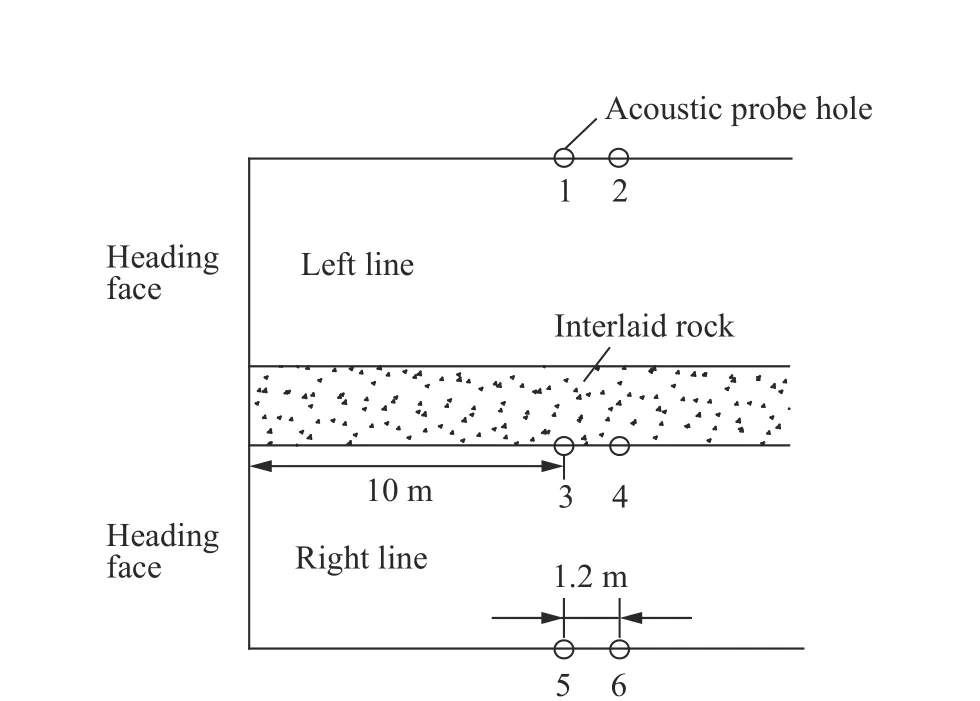
图5 孔位布置示意图Fig. 5 Arrangement of probe holes

3.2 测试仪器

现场测试采用智博联U5300 非金属超声探测仪，仪器由主机分析系统以及用于发射和接收超声波的声测管组成，其主要参数：单发双收通道，声时测读精度为25 ns，采样周期为25～409.6 ns，波形点数为512～4 096。测试时每两根声测管为一组，通过水的耦合，超声脉冲信号从一根声测管中的换能器发射出去，在另一根声测管中的换能器接收信号记录该脉冲波在介质内传播过程中表现的波动特征，测试现场如图6所示。

图6 声波现场测试Fig. 6 Acoustic test

3.3 岩体爆破损伤深度

根据探测布置位置，该处围岩级别为Ⅴ级，稳定性较差，双线隧道均采用双侧壁法开挖，如图7 所示（Ⅰ～Ⅶ代表开挖顺序）。由于测孔均布置在下台阶左右导坑的边墙上，而下台阶两侧导洞的炮孔布置如图8 所示（数字为雷管段号），其中炮孔直径为0.04 m，孔深均为1.4 m，辅助孔间距为1 m，周边孔间距0.6 m，周边孔距隧道轮廓线0.2 m。探测时，掌子面距测孔已推进10 m，后续的爆破对岩体的损伤影响不大，岩体声速现场实测数据见表4，根据表4 绘制声波速度-孔深关系曲线如图9 所示。

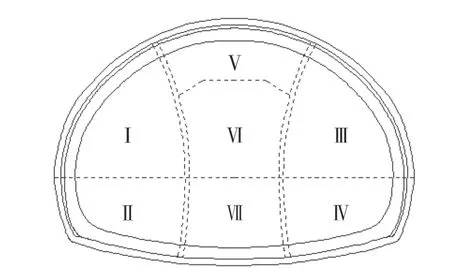
图7 施工顺序横断面Fig. 7 Cross section of construction sequence

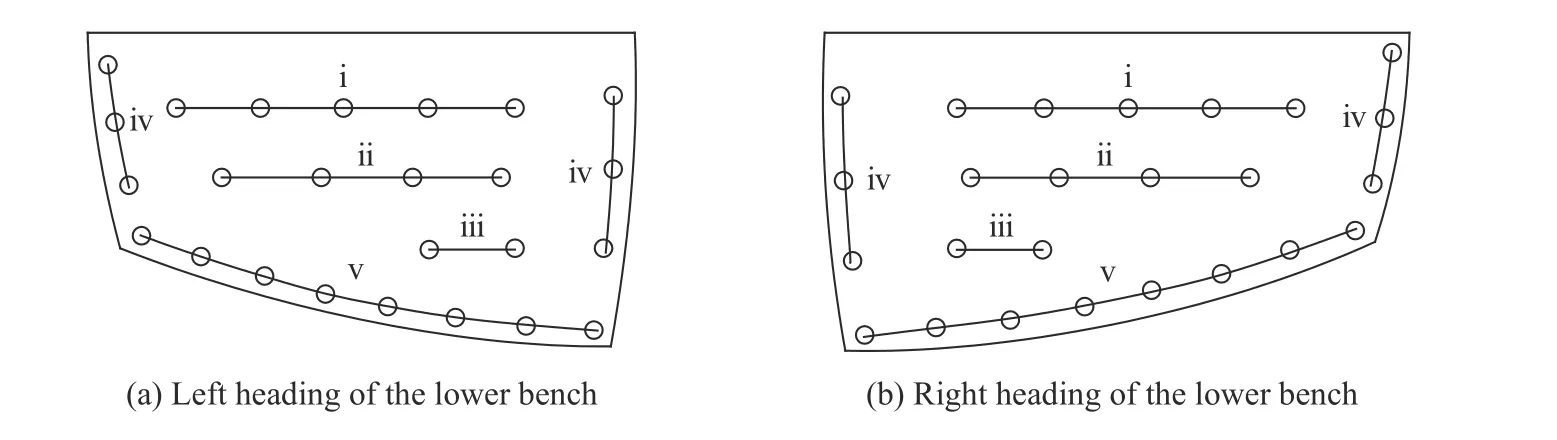
图8 炮孔布置Fig. 8 Layout of blast holes

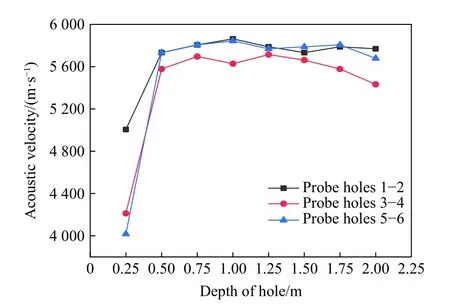
图9 声波速度-孔深关系曲线Fig. 9 Acoustic velocity varying with depth of hole

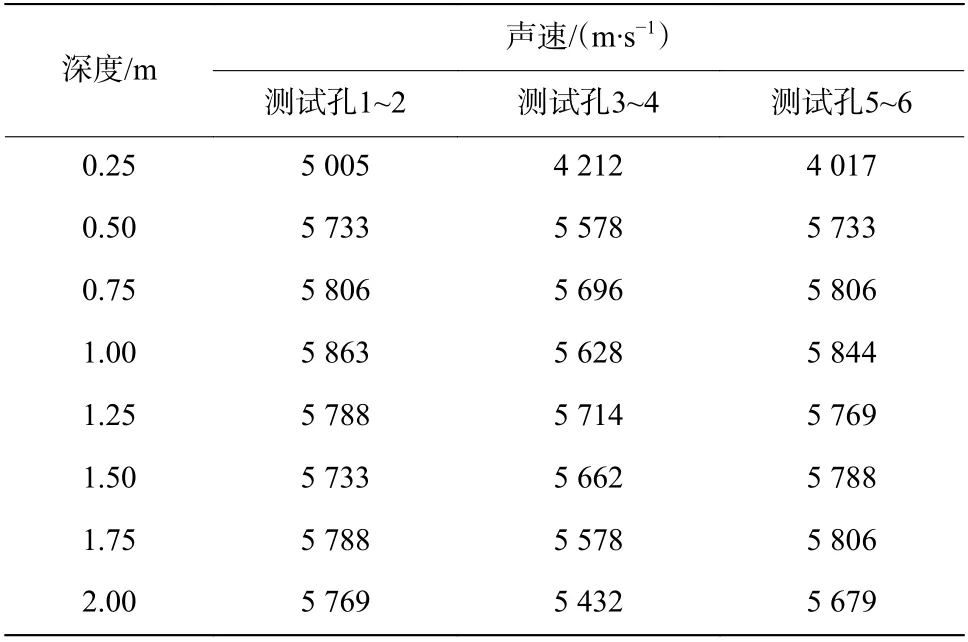
表4 岩体声速测试结果Table 4 Test results of acoustic velocity in the rock mass

由声波速度-孔深关系曲线可以看出，波速曲线在孔深0.50 m 前出现较大变化，波速下降明显，说明既有开挖爆破对围岩的损伤影响范围在0.50 m 左右。另外由于爆破时迎爆侧的围岩受到的扰动一般更大，因此中夹岩受双线隧道交替爆破开挖的影响下，其损伤程度较围岩其他部位要高，这在曲线图上也可以看出中夹岩3-4 断面整体波速较1-2 断面和5-6 断面要小。在深度达到0.50 m 后，波速测试结果均较稳定，这是由于随着深度不断加大，岩石的夹制作用也在增强，导致围岩的损伤发展受到限制。

根据数值模拟的计算结果，单个炮孔爆破引起的损伤影响范围在0.58 m，考虑到周边孔距轮廓线0.2 m，因此实际对围岩的影响范围应当在0.38 m，这与现场探测的损伤影响范围0.50 m 相接近，两者的误差在工程允许范围内，从而也验证了以建立的动态损伤本构用于损伤数值模拟的准确性。另外，需要指出的是，虽然在实际工程中围岩是随着隧道的掘进而受到多次的循环爆破作用，而本模拟只进行了一次爆破分析，但多次的循环爆破作用一般只会对损伤范围内的损伤程度有着明显影响，对造成的损伤范围则影响不大，因此在只考虑损伤影响范围的情况下比较数值模拟结果和损伤探测结果是合理的。