爆炸冲击波强间断问题的高阶伪弧长算法研究*
2021-12-03马天宝王晨涛赵金庆宁建国
马天宝,王晨涛,赵金庆,宁建国
(北京理工大学爆炸科学与技术国家重点实验室, 北京 100081)
双曲守恒律方程有着广泛的应用,在内爆动力学,惯性约束聚变,计算天文学,磁流体力学,计算爆炸力学,计算生物学等领域都和它密切相关。它有一个明显的特征,无论初值条件多么的光滑,随着时间的演化,最终都可能会演化为带有强间断的解。爆炸与冲击问题是强非线性的双曲方程,这些方程的解通常带有奇异性,也就是在解的附近存在较大的变化,包括激波,稀疏波,接触间断等。为了克服上述难题,一些高精度的数值格式被提出,如MUSCL、WENO[1-2]等。但采用高阶重构时,解在间断附近会产生虚假震荡。因此构造有效的高精度数值算法,不仅要求能捕捉到间断区域,同时又可以消除虚假震荡。针对虚假震荡的非物理现象,可以考虑将原始守恒方程映射到特征空间上[3],在特征空间上求得数值通量之后[4],再将通量映射回原始空间。这种通过对方程组多变量的耦合进行解耦的过程,可以巧妙地避开虚假震荡。
对于常规的有限体积方法,计算网格是均匀网格,若提高计算精度,那么相应的策略是增加网格数目。但是对于物理量梯度变化较小的区域,粗糙的网格便可以得到满意的结果,对光滑区域求解增加的计算量是没有必要的,因此这无疑在一定程度上降低了计算效率。基于此,根据解的性质,对网格进行合理的节点分布,对于高效、精确地计算双曲守恒方程有着极其重要的作用。伪弧长算法是解决这种问题的有效方法之一。在伪弧长算法中,网格节点会随着时间的变化而变化,在保证网格节点数目不变的情况下,在物理量梯度较大的区域自动加密,而在解较为平滑的区域自动稀疏。Tang 等[5]通过求解一个基于变分原理的网格方程得到了一种移动网格方法,2006 年Tang[6]将移动网格算法拓展到二维情况,近年来,自适应网格算法得到了较大的发展[7-9]。
本文将高精度的WENO 格式同伪弧长算法相结合,针对网格移动之后造成的网格非均匀和非正交使得通量的计算和网格物理量重构的过程较为复杂的现象,提出采用坐标变换,将坐标映射到均匀正交的计算坐标系下进行计算。结果表明这样可以提高数值精度。通过一维激波管问题结果的比较,可以看出伪弧长算法相较于传统的固定网格算法可以更好地捕捉到强间端,而高阶伪弧长算法对间断捕捉的分辨率最高。结果表明高阶伪弧长算法相较于有限体积以及低阶格式的伪弧长算法,它更适合处理处理爆炸与冲击强间断问题。此外,可以改变弧长参数使得网格移动更加明显,进而提高对间断捕捉的分辨率。
1 伪弧长算法
本文采用的伪弧长算法包含3 个部分:第1 部分给出物理空间的控制方程在时间和空间上的离散格式;第2 部分是坐标变换,将不均匀的物理空间变换到均匀的计算空间中进行求解;第3 部分则是伪弧长算法。
1.1 离散格式
考虑如下的双曲守恒系统:

对式(1)在网格 单元上进行积分,得到:

对上式采用Green 公式进行变换,则有:

数值通量采用局部Lax-Friedrichs 格式,详细定义如下:

式(3) 可以写成半离散格式:

以下仅对x方向进行离散,y方向仅需要将变量i替换为j即可。

对于时间的离散,忽略掉网格的索引i,j,则采用如下的四阶TVD-RK 格式:

式(8)和式(9)的重构中,重构的物理量可以选择原始变量,守恒变量以及特征变量。由于欧拉格式的非线性性质,采用高阶格式容易引起非物理震荡,因此可以考虑采用将变量映射到特征空间中,在特征空间中进行重构,重构完成之后再映射回原始空间,具体计算如下:

1.2 坐标变换
在伪弧长算法中,移动之后的网格是非均匀网格,而传统的数值格式均是基于均匀网格给出的。通过限制网格的移动距离,可以近似用传统的格式进行插值运算,然而仅仅在一阶或者二阶情况下,这种插值引起的误差不大。若直接运用到高阶格式,将会引起较大的误差。因此,对于高阶伪弧长算法的通量计算,必须考虑网格尺度的影响。为了解决这种问题,通常有两种策略,第一种策略是将网格尺度引入WENO 格式的非线性权重,然后直接进行构造高阶格式[11-13]。这种构造清晰明了,但是格式较为复杂,而且不易推广到二维或者三维情况。另外一种策略是转换坐标系,将当前坐标系变换到曲线坐标系下,因为曲线坐标系中计算网格是均匀正交的,因此可以直接用传统的格式进行通量计算。详细变换如下。
引入曲线坐标

则式(1)可以由原始坐标转换到曲线坐标下进行计算,即


1.3 网格移动算法

伪弧长控制函数取为

为了保证网格的光滑性,可以用低通滤波器进行光滑处理,一维情况表达式为
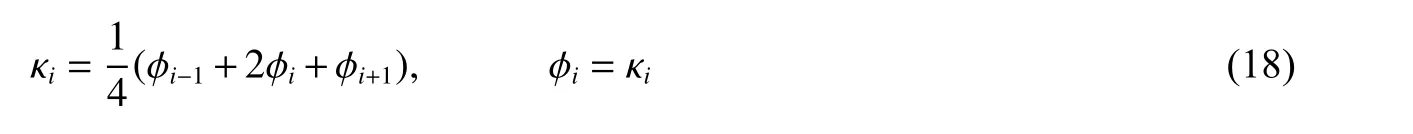
二维情况采用下述公式

具体光滑处理次数应该视情况而定,通常情况下处理2~3 次即可,若非线性情况较严重,可以处理10 次左右。
因此方程(16)改写为

通过对式(20)的计算,可以求得网格的分布。式(20)的计算可以采用Jacobian 迭代进行计算,计算步骤如下


因此根据式(21)可以得到式(13)的网格移动速度为

式中:∆t为时间步长。
网格移动完成之后,接下来的工作就是需要得到物理量在新网格上的值,这一重要步骤又称物理量重映。常用的物理量重映方法分为2 类,一是基于通量的物理量重映方法,二是基于网格相交的精确积分守恒重映方法。考虑到在相邻的时间间隔要求,网格移动距离较小,而且网格始终处于保凸性,因此本文采用的映射方法为第一种。

图1 新旧网格转化示意图Fig. 1 Diagram of old grid transforming to new grid

综上,伪弧长算法的详细步骤如下。
第2 步,求解网格控制函数式(17),并用式(18)和式(19)进行光滑打磨控制函数。

第4 步,物理量映射,根据式(23)更新新网格下的物理量。
第5 步,求解物理量控制方程:(a)如果采用低阶伪弧长算法,则直接在物理空间进行求解。通过等式(10)更新时刻的物理量;(b)如果采用高阶伪弧长算法,则利用式(12)、式(13)和式(14)将物理空间的物理量转换到均匀计算坐标系下进行求解。通过式(10)更新时刻的物理量,求解完成之后根据逆变换再把物理量映射回物理空间。
第6 步,如果求解达到终点时间,则程序终止,否则转到第2 步。
2 一维数值算例
下面基于伪弧长数值算法进行一些算例测试,由于上面的理论是基于二维情况推导的,对于一维情况直接进行降维处理,然后再计算即可。限于篇幅这里不再详细说明一维的理论。此外,以下所有数值算例均采用无量纲进行计算,伪弧长控制函数均采用式(17)计算。
2.1 一维Euler 方程激波管问题
初值条件:

计算域为[−5,5],终止时间为tmax=,伪弧长控制函数(17)取为=(1, 5),边界条件为自由输出边界条件,计算结果如图2 所示。
上面的计算均是在150 个网格数目下求得的,其中参照解是采用20 000 个固定网格下结合五阶特征变换进行计算的。其中MUSCL,WENO-5,WENOCV-5 分别代表的是固定网格下用二阶MUSCL,五阶WENO,五阶特征变量WENO 格式计算;而PALM-2, PALM-5 代表的是在采用二阶伪弧长和五阶伪弧长的格式计算。
从图2(a)中可以看出在固定网格下,高阶格式相对于低阶格式可以更加精确地捕捉到间断,但是从局部放大中可以看出,五阶固定网格在间断附近产生了数值震荡,这是高阶格式带来的弊端,因此可以通过特征变换进行求解,进行特征变换之后,高阶格式消除了局部震荡,整体解的光滑性较好,因此可以经过特征变换得到较为满意的结果。从图2(b)中可以看出,伪弧长算法可以很容易的捕捉到间断面,而且二阶伪弧长算法对间断的捕捉几乎接近于固定网格下五阶的捕捉程度,但是弱于伪弧长五阶算法。因此这说明了高阶伪弧长算法是有效的。图2(c)是网格的运动轨迹,说明伪弧长算法很好地控制了网格的自适应移动,使得网格在梯度较大的区域进行加密,进而捕捉到间断解。
2.2 一维爆炸问题
初值条件:

该算例的计算域为[0,1],终止时间tmax=0.038,两套伪弧长控制函数分别取为(a1,a20,20),(a1,a2)2=(10,80),边界条件为固壁反射条件,计算结果如图3 所示,其中2-1, 2-2, 5-1, 5-2 分别代表二阶和五阶分别采用系数和系数时的计算结果,可以看出,当采用不同的系数时,逼近的分辨率也不同。

图3 一维爆炸算例计算结果Fig. 3 Results of one dimensional explosion example
该算例是一个爆炸问题的算例,是检验高精度格式的经典算例。普通低阶格式在网格数目较少的情况下很难捕捉到强间断,而且在计算的过程中,由于稀疏波的传播,压力接近于零,使得计算容易产生负值,导致程序终止。因此,在计算的时候均采用了保正性条件,详细的保正性理论可以参考文献[9]。图中的参照解是在固定网格下用五阶特征变换在网格数为25 000 下进行计算得到的。
从上面的计算结果可以看出,二阶固定网格耗散较强,对最高点的捕捉能力较弱;五阶固定网格较二阶提升很大,可以较为清晰的捕捉到多个间断点,而且在间断点附近耗散性非常小;二阶伪弧长算法较固定网格算法有一定提升,固定网格对断点的捕捉能力很弱,耗散性较强,而采用伪弧长算法以后,耗散能力减弱,对间断点的捕捉能力增强;采用五阶伪弧长算法最为满意,各个间断点都可以较为准确的捕捉,而且在间断点邻域的结果和参照解也最为接近。
通过网格的轨迹线图,可以看出在t=0.027 时刻附近,两个冲击波相遇,同时伴随着稀疏波的传播,正是因为稀疏波的传播,造成压力过小,接近于零。这样,采用普通的通量差分格式计算会因为计算机的浮点误差和计算格式的数值误差造成物理量为负,从而导致程序的终止。因此需要采用特殊的格式进行修正才能保证程序的进行,本文采用了保正性格式进行限制。
3 数值精度验证
3.1 一维精度验证


表1 有限体积法与伪弧长算法在不同网格数下的误差和精度Table 1 Numerical errors and precision of FVM and PALM changing with grid numbers (example 3)
3.2 二维精度验证
采用二维两步化学反应流来测试伪弧长算法的范数误差和收敛阶。对应式(1)的详细表达式如下:


采取构造一组人为解进行数值验证。相应的源项需要根据人为解进行修正。其中构造的人为解详细如下:

表2 给出了二维验证计算结果,可以看出,随着计算网格的加密,误差在逐渐减小,而且收敛阶和算法本身较为吻合。通过图4 可以看出,高阶有限体积算法对等密度图的捕捉较低阶有限体积更为精细,而且采用伪弧长算法之后,网格自动在物理量梯度较大的区域进行自适应加密,同时也没有失去解的准确性。

表2 有限体积法与伪弧长算法在不同网格数下的误差和精度Table 2 Numerical errors and precision of FVM and PALM changing with grid numbers (Example 4)

图4 密度云图(T =2π,网格40×40)Fig. 4 Density contours (T =2π,grid 40×40)
4 爆轰化学反应流的计算
4.1 一维化学反应流
一维爆炸冲击问题,控制方程取为如下:

初值条件:

伪弧长控制函数取为 (a1,a2)=(0.5,5),边界条件为反射边界,终止时间T=0.1。计算结果如图5 所示。

图5 一维化学反应流密度Fig. 5 Density of one dimensional chemical reaction flow
一维化学反应流的参照解是基于5 000 个固定网格结合特征变换进行计算的,而二阶格式采用的是120 个网格,五阶格式采用的是120 个网格。可以看出,在固定网格下,五阶格式对间断的捕捉要优于二阶格式,而经过伪弧长的变化之后,二阶格式也可以较为准确是捕捉到强间断。对解捕捉的最好结果是采用了五阶伪弧长格式,它对网格捕捉的分辨率最高,图中可以看出高阶伪弧长和参照解几乎重合。这充分说明了高阶伪弧长格式的优越性。在本算例中,由于压力的初值变化跨越了10 个数量级以上,计算时采用的变量均为原始守恒变量,并没有采用局部特征变换,从而导致在间断附近存在微小震荡。采用了伪弧长算法,并没有完全消除震荡,但是却很明显的减弱了数值震荡,这说明伪弧长算法对于减弱方程的奇异性有着很好的效果。需要注意的是,由于爆炸冲击问题的强烈的奇异性,常规的高阶格式会因为计算物理量为负,而导致程序终止。在本文中,修正式(7)的 ε=10−15,并结合保正性算法[9],这样才能使得程序可以继续计算。此外可以看到,网格的的轨迹得到了很好的自适应,它在解梯 度较大的区域自适应加密。
4.2 二维化学反应流前台阶爆轰问题
计算域为 [0,3]×[0,1]。 障碍物的区域为 [1,3]×[0,0.4],伪弧长控制函数取为 (a1,a2)=(2,0.2),初值条件取ZND[10]的解析解作为初值。控制方程采用式(27)两步化学反应流。边界条件:除了左右两侧,其他均设为反射边界。左右两侧为流入流出边界。终止时间T=0.22。图6 为各方法给出的T=0.22 时刻的状态。

图6 一维化学反应流压力Fig. 6 Pressure of one dimensional chemical reaction flow

图7 一维化学反应流的网格轨迹Fig. 7 Mesh trajectory of one dimensional chemical reaction flow

图8 二维化学反应流图Fig. 8 Results of two dimensional chemical reaction flow
图6 的参照解是采用了1200×400网格数结合五阶WENO 有限体积进行计算的结果。其余计算均在 360×90网格下进行计算。通过对比可以发现伪弧长算法都较为准确的捕捉到了爆轰反应的细节,对爆炸冲击波阵面都得到了较为精确的捕捉,而且用伪弧长五阶算法的结果和参照解的结果更为接近,并且在局部拐角区域,高阶算法对细节的捕捉更为精确。这说明了高阶伪弧长算法收敛速度较快,因此可以更好地处理爆炸与冲击强间断的问题。
5 结 语
本文将高精度数值算法和伪弧长算法进行结合,较为详细的介绍了高阶伪弧长算法从推导到应用的过程。针对高阶伪弧长算法在处理通量计算和网格变换之后的物理量重构中的难题,通过引入计算坐标,经过坐标变换将计算过程转换到曲线坐标系下进行计算。通过构造的人为解,验证了高阶伪弧长算法的数值精度。
各算例的计算验证表明:伪弧长算法相较于有限体积算法可以更成功地捕捉到强间断;而且高阶伪弧长算法对强间断的捕捉相对于传统高阶有限体积法和二阶伪弧长算法有更大的优势,它可以以更少的网格数目获得更高的分辨率。
本文采用伪弧长算法结合高阶WENO 有限体积格式进行计算,有限体积格式在处理物理量重映过程中的过程较为繁琐,而且对网格移动的限制较为严格,要求每两步网格迭代变化的距离不能太大。因此为了提高计算效率,可以尝试采取有限差分进行计算,有限差分结合动网格和坐标映射可以避免物理量的重映过程,因此可以适当提高计算效率。为了提高计算精度获得高分辨率的结果,而且又不需要很高的网格数目,可以采用高阶伪弧长算法进行计算,它可以以较少的网格数目得到较为满意的结果,从而提高计算效率。
