男性青年不同坡角斜面行走的步态特征研究

杨子涵，刘卉，蒋量，王立端，万祥林，曲峰

在日常生活（步道、楼房出入口、过街天桥）和体育休闲中，常常需要面对不同斜坡环境。斜坡坡角的改变将导致重力相对行走表面方向改变，这种变化对步态有显著影响[1]。研究指出，当行人上下斜坡时，跌倒风险随之增加[2]。一般来说，城市中较陡的路面降低了人的行走意愿[3]。日常生活中斜坡的普遍存在且影响不一，因此了解步态为适应斜坡行走所做的改变是十分重要的。

目前，国外对斜坡行走的步态分析包括时空参数分 析[4-13]、运 动学 分 析[4，6-7，10-11，13-14]、动 力 学 分 析[7，10，15-17]和适配的假肢矫形器设计[18]，国内在斜坡对步态影响的研究近年来刚刚开始[19-22]。一般认为，在上坡行走时为了提高重心，支撑腿需要产生更大的踝关节趾屈力矩和伸髋力矩[7-8]；下坡时则更注重控制行走时身体的持续加速[23]，同时要求更大的伸膝力矩及踝关节运动幅度[7]。这些特点对于肌力减少的人群，如老年人和行动受限人群会更加明显[8，18，24]。目前，许多斜坡步态的研究通过跑步机来进行，这种固定步行速度方法的研究在动力学方面与真实环境中的研究存在差异[25]。通过有限的基于自选步速的斜坡研究得出的步速步长变化规律并不一致，共有4种不同类型[5-8]。有研究进一步指出，在斜坡步态研究中，对于通过自选步速在斜坡上行走产生的步态改变还没有得到充分研究[6]，如以自选速度在大坡角范围内行走的步态改变及控制策略的改变起始坡角。

因此，本研究通过探讨3种坡角斜坡以自选速度上下行走时的步态，并与平地行走对比，旨在评估坡角对男性青年行走时下肢关节角度力矩的影响，并进一步分析不同斜坡对行走步态控制策略的改变。本研究假设不同坡角会对上下坡行走与平地行走之间的控制策略即关节角度力矩造成显著改变，同时假设这个改变产生于±6°。本研究将为坡面行走步态特征的相关基础研究和斜坡行走康复训练、运动鞋及矫形器具设计、机器人设计等提供相关参考。

1 研究对象与方法

1.1 受试者

受试者为10名男性青年，年龄（23.7±1.1）岁，体重（67.5±5.0）kg，身高（174.8±4.55）cm，身体健康，无上下肢神经及肌肉损伤病史，惯用脚均为右脚。

1.2 试验方法

测试斜坡环境由铝型材搭建，步道表面铺有木板供行走，测力台水平安装于3.2 m长的步道中央，并与周围木板有5 mm间隔[26]。斜坡角度调整装置位于步道一端，角度调整精度为±0.5°。每位受试者在接触测力台前后至少有2个单步，测试的4个坡角选择（0°，6°，12°，20°）参考前人研究[7，10，17，27]。受试者身着泳裤，根据H.HAYES模型在身上粘贴29个反光标志点[28]。试验开始前，要求受试者先在平地上以个人习惯步速行走5次，并告诉受试者在接下来的斜坡上行走时尽量保持该速度，在4个坡角中随机选择一个坡角作为起始测试坡角，并先在该斜坡坡角上下行走5次用以习惯该坡角。正式试验时通过8台红外动作捕捉镜头（Motion Analysis Raptor-4，USA，200 Hz）和1块测力台（Kistler 9281CA，Switzerland，1 000 Hz）配合Motion Analysis自 带 软 件Cortex（version 2.6，Motion Analysis Corporation，Santa Rosa，CA）同步采集运动学及动力学数据。以右脚完全踩到测力台记为1次成功行走，在记录3次成功行走数据后，受试者休息5 min从而消除自适应以及肌肉疲劳对结果的影响并准备下一次测试。

1.3 数据处理

采 用MATLAB R2016a（The MathWorks Inc.，USA）进行，运动学和动力学数据均采用4阶Butterworth低通滤波法进行平滑，截断频率分别为8 Hz和15 Hz[15]。每个坡角下，测力台都通过Cortex软件进行数字化并将测力台的反作用力转换在大地坐标系表示。转换后的测力台力值数据通过逆动力学方法计算下肢关节三维净力矩，步态周期的定义为单侧足跟着地时刻到同侧足跟再次着地，步态周期中的足跟着地及趾离地时刻通过斜坡测力台力值大于10 N的条件标记，足跟再次着地时刻通过观察标记[7]。

在1个步态周期中，支撑相摆动相中不同时期的划分标准参照前人研究[29]，对惯用腿侧下肢的髋膝踝3个关节的角度-时间及力矩-时间变化曲线都选取几个特征时刻（见表1）进行统计分析。

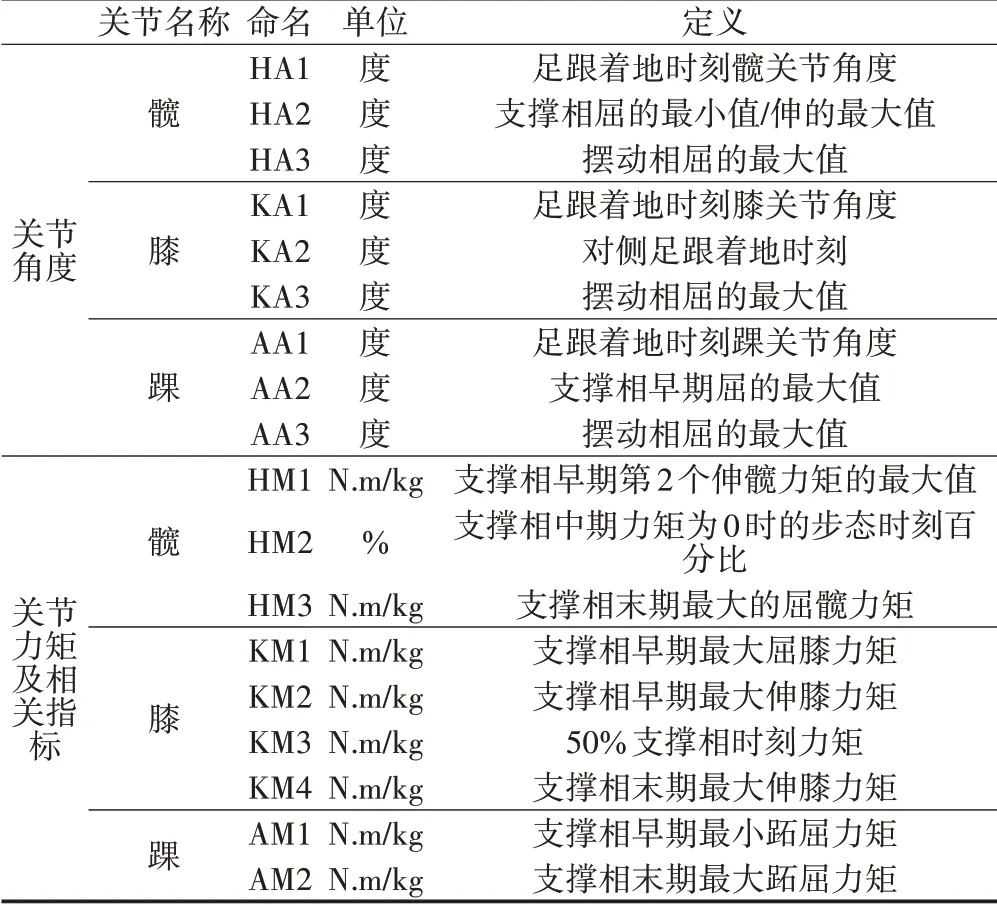
表1 髋膝踝特征时刻的命名与定义Table1 Naming and Definition of Points of Interest from Kinematic and Kinetic Data of Hip，Knee and Ankle

每个受试者的每次步行中，将之前所得到的下肢三关节角度-时间变化曲线和力矩-时间变化曲线中都以右足跟首次触地（踏上测力台）表示1个步态周期开始时刻，以右足跟再次触地表示1个步态周期结束。将所得到的完整步态阶段通过Origin软件进行标准化。将X轴坐标0时表示右足跟触地时刻，60表示右足尖离地时刻，100表示右足跟再次着地时刻，进行插值。其中，角度-时间变化曲线正值为屈，负值为伸（踝关节正值为跖屈，负值为背屈），力矩-时间变化曲线正值为伸，负值为屈（踝关节正值为跖屈，负值为背屈）。在每个步态周期中都选取一定数量的关键点来标注特征时刻进行统计分析。

1.4 统计分析

应用SAS9.4（SAS Institute Inc.，USA）统计软件对不同坡角下（-20°、-12°、-6°、0°、6°、12°与20°）各步速、步频、步长及下肢各关节各特征时刻结果分别进行单因素重复测量方差分析，显著性水平定义为0.05。当不同坡角对结果影响显著时，后继检验采用Dunnett方法比较不同坡角与0°结果的显著性，显著性水平定义为0.05。

2 结果

不同坡角条件下步速、步频、步长结果显示，坡角的 改 变 对 步速[F（6，54）=15.84，P＜0.001]、步 频[F（6，54）=23.72，P＜0.001]和步长[F（6，54）=14.74，P＜0.001]有显著影响。后继检验显示，与0°坡角相比，当坡角≥12°及坡角为-20°时，步速显著减少；当坡角=20°时，步频显著减少；当坡角≥-12°时，步频显著增大；当坡角大于或±12°时，步长显著减少（见图1）。

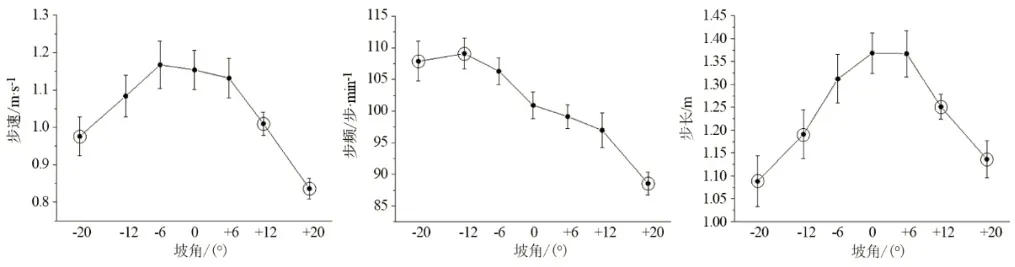
图1 不同坡角下的步速、步频、步长结果（M±SD）Figure1 Mean（SD）of the Gait Spatiotemporal Parameters for Each Grade

不同坡角条件下上坡行走及下坡行走的下肢髋膝踝角度及标准化力矩趋势在单个步态周期中的结果见图2，关节角度及力矩特征时刻值结果见表2。

表2 下肢关节角度及力矩特征时刻结果（M±SD）Table2 Mean（SD）of the Joint Kinematic and Kinetic Points of Interest for Each Grade

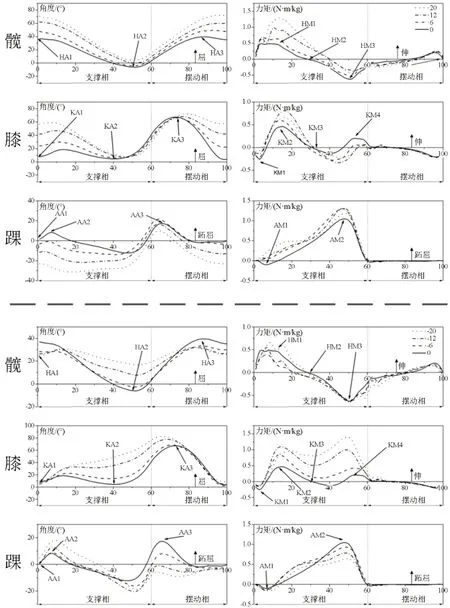
图2 不同坡角下肢髋膝踝角度及标准化力矩在1个步态周期中的变化Figure2 Sagittal Joint Angles and Normalized Moments as a Function of the Gait Cycle

（1）髋关节角度、力矩特征时刻结果。坡角的改变对髋关节角度特征时刻各结果有显著影响，具体为足跟着地时刻髋关节角度（HA1）：F（6，54）=387.98，P＜0.00；支撑相屈的最小值/伸的最大值（HA2）：F（6，54）=39.00，P＜0.001；摆动相屈的最大值（HA3）：F（6，54）=319.16，P＜0.001。坡角的改变对髋关节力矩特征时刻各结果有显著影响，具体为支撑相早期第2个伸髋力矩的最大值（HM1）：F（6，54）=26.65，P＜0.001；支撑相中期 力 矩 为0时 的 步 态时 刻 百分 比（HM2）：F（6，54）=44.78，P＜0.001；支撑相末期最大的屈髋力矩（HM3）：F（6，54）=9.07，P＜0.001。

（2）膝关节角度、力矩特征时刻结果。坡角的改变对膝关节角度特征时刻各结果有显著影响，具体为足跟着地时刻膝关节角度（KA1）：F（6，54）=207.69，P＜0.001；对侧足跟着地时刻（KA2）：F（6，54）=267.29，P＜0.001；摆 动 相 屈 的 最 大 值（HA3：F（6，54）=21.33，P＜0.001。坡角的改变对膝关节力矩特征时刻各结果有显著影响，具体为支撑相早期最大屈膝力矩（KM1）：F（6，54）=387.98，P＜0.05；支 撑 相 早 期 最 大 伸 膝 力 矩（KM2）：F（6，54）=7.83，P＜0.001；50%支撑相时刻力矩（KM3）：F（6，54）=35.74，P＜0.001；支撑相末期最大伸膝力矩（KM4）：F（6，54）=210.80，P＜0.001。

（3）踝关节角度、力矩特征时刻结果。坡角的改变对踝关节角度特征时刻各结果有显著影响，具体为足跟着地时刻踝关节角度（AA1）：F（6，54）=79.96，P＜0.001；支撑相早期屈的最大值（AA2）：F（6，54）=213.19，P＜0.001；摆动相屈的最大值（AA3）：F（6，54）=28.92，P＜0.001。坡角的改变对踝关节力矩特征时刻各结果有显著影响，具体为支撑相早期最小跖屈力矩（AM1）：F（6，54）=41.70，P＜0.001；支 撑 相 末 期 最 大 跖 屈 力 矩（AM2）：F（6，54）=59.34，P＜0.001。

3 讨论

图1显示，步长步速在斜坡行走时随坡角变化呈倒U型趋势，与J.SUN等[12]在城市环境中观测到的结果一致，但与前期依据实验室环境得到有关自选步速的斜坡步态测试结果不一致。不一致表现为步长及步速增加[8]、无改变[7]、减少[6，9，12]和上下坡之间趋势不同[5，10]。研究结果的差异性可能是由测试环境的不同造成的，如跑步机或搭建含测力台步道的使用，斜坡的坡角大小及测量范围、斜坡的长度和宽度、扶手使用与否和摩擦系数大小等。本研究与J.SUN等[12]通过影像记录的2 400名城市行人的步态时空参数规律一致，这增加了本研究结果的代表性。

3.1 上坡行走

人体在上坡行走时，下肢角度及力矩变化趋势显示（见图2），着地时刻下肢髋（HA1）膝（KA1）踝（AA1）角度随坡角增大而增大，支撑相早期踝关节跖屈的最大值逐渐变小（AA2）转为背屈，摆动相髋关节屈的最大值（KA3）也表现出更大的屈曲。随着坡角增大，下肢关节屈伸幅度增大的变化是为了适应上坡而做出的相应改变，其中变化最大的是足跟着地时刻髋关节角度（HA1），从平地到20°坡角后增加了33.53°（91.1%）。平地行走时，最小跖屈力矩（AM1）一般被认为有助于足跟着地后减缓全掌着地速度，然而随着坡面倾斜角度的增加，其由背屈逐渐变成完全的跖屈力矩。支撑相末期最大跖屈力矩（AM2）随着坡面倾斜角度的增加而增加。AM1由背屈变为跖屈以及AM2峰值的增大说明在上坡坡角增加的情况下，需要增加踝关节跖屈力矩大小及跖屈时间百分比来保证正常步行。膝关节在支撑相早期最大屈膝力矩（KM1）随倾斜角度增大其缓冲的作用减少。支撑相末期最大伸膝力矩（KM4）表现出因倾斜角度增大而减少了对支撑相末期伸膝的需求。髋关节支撑相早期第2个伸髋力矩的最大值（HM1）随倾斜角度增大表现出伸髋力矩增大，表现出为了适应坡角的增大产生更大的伸髋力矩，用来弥补对侧腿伸膝力矩（KM4）的减少，从而完成上坡。支撑相中期力矩为0的时刻（HM2）明显后移，说明在支撑相中花费更多时间百分比来完成伸髋过程，结合HM1的增加与HM2的后移说明在上坡坡角增加的情况下，需要增加人体伸髋净力矩与延长伸髋时间百分比来保证正常步行。支撑相末期最大的屈髋力矩（HM3）则随坡角增加而增加，说明在上坡行走时支撑相末期髋关节屈力矩的减少可以帮助提高重心高度并维持正常行走，其中变化最大的是髋关节第2个伸肌力矩的最大值（HM1），从平地到20从坡角后增加了0.79 N.m/kg（138.6%）。

综上所述，随着坡角的增加，上坡需要增加摆动腿的屈髋屈膝，同时加强踝背屈来帮助足廓清，而支撑腿在摆动腿开始摆动时，伸膝伸髋同时踝跖屈将有助于提升人体重心高度，增大摆动半径，从而保持步长。踝关节从单侧足着地时刻开始在整个支撑相中基本都处于背屈（伸）状态，使原本在支撑相中-末期的踝关节角度变化由背屈-跖屈逐渐过渡为跖屈，这种转变的时间百分比随斜坡倾斜角度的增大而愈加明显，并伴随跖屈力矩增加，表现为踝关节在大坡角上坡行走时将花费更多时间、做更大功来完成跖屈过程。在人体上坡行走外，除踝关节跖屈力矩外，髋关节伸髋力矩的时间百分比及峰值都有所增加，膝关节支撑相早期伸膝力矩峰值有增加的趋势，他们共同表现出一种推进的状态。

3.2 下坡行走

人体在下坡行走时，下肢角度及力矩变化趋势显示（见图2），随着坡角增大，着地时刻髋角着地时刻（HA1）减少，支撑相阶段，足支撑相早期屈的最大值（AA2）跖屈增大，对侧足跟着地时刻（KA2）膝关节屈增大，同时髋关节支撑相（HA2）屈曲增加。摆动相踝关节及膝关节屈最大值（AA3，HA3）逐渐变小，摆动相屈的最大值（KA3）逐渐变大。随着坡角增大，膝踝关节屈伸幅度增加、髋关节屈伸幅度减少是为了适应下坡变陡而做出的相应改变，变化最大的是对侧足跟着地时刻（KA2），从平地到20°坡角后增加了47.77°（444.8%）。力矩方面，下坡时更多的力矩变化产生在膝关节和踝关节，其中踝关节支撑相末期最大跖屈力矩（AM2）随着坡面倾斜角度的增加而减少。支撑相早期最大屈膝力矩（KM1）有一定增大，表现为通过膝关节的屈曲降低重心的作用，支撑相早期最大伸膝力矩（KM2）、50%支撑相时刻力矩（KM3）随坡角增大表现出更大的伸力矩。结合角度变化，表现为支撑相中期支撑腿主要作用是屈膝来降低重心高度，支撑相末期最大伸膝力矩（KM4）随坡角增大表现出更大的伸力矩，原因是此时膝关节角屈曲增大，使得膝关节周围肌肉产生更大伸膝力矩来维持躯干平衡。在下坡行走中，支撑相末期最大伸膝力矩（KM4）变化最大，从平地到20平坡角后增加了1.2 N.m/kg（500%）。

综上所述，随着坡角的增加在下坡时需要通过不断屈膝以及维持髋的屈曲来控制重心的下降，同时踝关节着地时产生更多跖屈及在支撑相末期产生更大背屈趋势来维持行走的稳定性。随着坡角增加，原本膝关节角度变化在1个步态周期中从屈曲-伸展-屈曲变化为持续的屈曲，同时膝关节力矩也基本全部变为伸膝力矩，这种趋势变化表现为在足跟着地后，通过控制膝关节屈曲与踝关节屈伸来降低重心维持步态。

3.3 小结

本研究通过对比人体上坡、下坡下肢关节角度力矩与平地步行时下肢关节角度力矩的峰值与特征时刻，探究不同斜坡角度对步行时下肢关节运动学与动力学的影响。首先假设不同坡角会对上下坡行走与平地行走之间的控制策略即关节角度力矩造成显著性改变，同时假设这个改变将在±这个坡角产生。研究结果显示，上下坡行走与平地行走之间关节角度力矩特征值及特征时刻因坡角改变而产生显著改变，同时本研究运动学趋势与前人研究相一致[7，10，30]，动力学趋势与部分前人研究一致[10，15，17，31]。本研究中髋关节力矩的变化趋势及统计结果不足以支持A.N.LAY等[7]的观点，特别是在上坡行走中，并未观察到髋关节在支撑相末期有伸膝力矩峰值的产生。相反的是，观察到髋屈力矩具有减少趋势，造成这种不同趋势的可能原因是A.N.LAY等[7]的研究中步态时空参数在各个坡角下无差异导致的。

有研究指出，步态的改变在面对斜坡坡角为10°时就已经出现[7]。另一份调查受试者上坡行走时迈上斜坡的第1步，发现产生步态改变的坡角应该介于6°~9°之间[14]。本研究结果显示，坡角在±角在时，下肢关节角度力矩特征值及特征时刻已经出现显著改变。结果不同的原因可能在于并未只在斜坡上行走，而是单步登上斜面。本研究结论指出，当坡角达到±坡角时，斜坡已经对下肢关节角度力矩特征值和特征时刻产生显著影响，在未来研究中增加不同坡角对功率及下肢关节做功的影响有助于加深坡角大小对人体步态影响的了解。虽然本研究并未进行上下坡步态间的对比，但因为上坡步行与下坡步行之间角度力矩的变化趋势及控制模式不一致，上下坡的步态控制模式变化可能始于不同的斜坡坡角。

4 结论

步长与步速在斜坡行走中随坡角增大呈倒U型关系。上坡、下坡与平地行走之间通过不同的控制方式来进行：上坡行走主要以增加下肢关节的屈伸幅度及下肢伸力矩从而增加输出功率的推进为主；下坡行走主要以维持髋关节屈曲的同时增加膝踝关节的屈伸幅度并增加膝关节伸力矩来降低重心，保持身体稳定性为主。人体平地行走步态在坡角达到±6°时已经产生显著改变。