多元表征，实现高阶计算思维发展

侯玉茹

【摘 要】表征就是把数学客观对象的外在形式（实物、模型、图像、文字、符号等外在表征）与学生内在心理编码（言语码、心象码、整合码等内在表征）进行交互对应，构建意义，而多元化的表征可以有效实现数学知识的多元建构、数学技能的多元训练、数学经验的多元积累。多元的表征之间相互递进，实现数学计算思维的高阶发展。要注重内在表征的多元化外化呈现，使数学计算思维可视、可感、可具体表达，最终抽象为高阶计算思维。

【关键词】多元表征 高阶计算思维 数学

一、动作表征，高阶计算思维的可视化

动作表征是一种动态的表征形式，学生通过动手操作活动，挖掘数学本质，建立数学模型。数学是一门抽象性、逻辑性很强的学科，而小学生的思维正处于由具体形象思维向抽象逻辑思维过渡的阶段，在此阶段要将问题转化为具体的现实操作，才能凸显出原问题的本质结构。可见，动作表征正是架在数学知识抽象性和学生思维形象性之间的一座“桥梁”。因此，在数学教学中，要让学生亲身参与，动手操作，动脑思考，把抽象的知识变成看得见、讲得清的现象，从而了解数学知识内在的联系，化难学为易学。

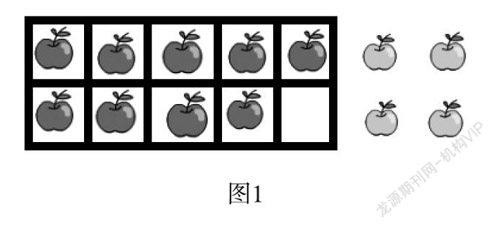
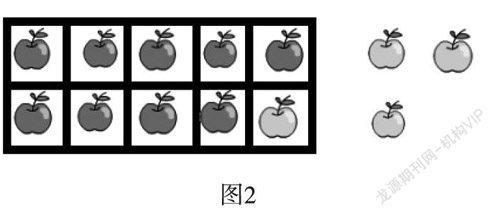
例如，笔者在教学“9+几”这一课时，主题图（如图1）是小猴在数苹果，盒中有9个红苹果，盒子外面有4个青苹果，求一共有多少个？学生根据以往的学习经验，知道盒子中的苹果数+外面的苹果数=苹果总数，但这节课的教学重点和难点是让学生理解凑十的过程，能用凑十法解决“9+几”的问题。为了更好地体现凑十的过程，将教材中小朋友的方法“先放进1个凑成10，10加3得13”这句话转化成学生自己的动作、自己的理解，笔者让学生利用方格纸（如图2）进行操作，学生通过自己的操作，觉得应该先从外面的4个中拿出1个放进盒中，这样9个就变成了10个，再加上外面的3个，一共是13个，数与形有效结合。

图1

图2

别看这个小小的移动苹果的动作，它帮助学生非常形象地理解了“凑十”这一抽象的方法，为接下来学习8、7、6加几的凑十法打下了扎实的基础。

在学生进行数学活动时，教师应给学生提供丰富的素材，这样才能得到多样化的反馈。所以“9+几”这课除了利用教材中的素材，通过刚好能放十个的盒子感知凑十，还要补充让学生动手摆小棒的操作。这时会发现：有的学生是从4根里拿出1根和9根捆起来就是10，10加3就是13;还有的学生是通过9根继续往下数4根，数到13。这种多样反馈是很有必要的，第一种类型的学生已经能联系之前学习的十加几等于十几，想到先凑十，再计算。学生们自我强化了凑十的思想，思维得到了进阶。显然，第二种类型学生的思维水平还停留在数数阶段。具象学生的思维之后，我们就能更好地针对不同类型的学生做出调整。接着我们再给学生提供计数器，让学生经历具象的、直观的数学操作。反馈的结果又有不同：有的学生用计数器直接拨出结果;有的学生将计数器上个位拨满十以后没有退位导致个位上有10颗算珠;有的学生在计数器个位上先拨9再拨下一个珠的时候，知道要把个位全部退掉十位上拨1颗算珠，再接着拨，最后得出结果。其实“9+4”的结果很简单，但是增加了计数器这个工具后，学生们的计算思维变得可视化了，体现了不同层次的思维水平。显然，学生在使用计数器的过程能联系之前学习的位值制，体会到十进制“满十进一” 的内涵。教师还可以补充介绍算盘，让学生课后研究如何利用算盘进行计算。

因此，数学教学活动中，教师要向学生提供充分参与数学活动的机会，使多种思维可视化，让学生在各种思维碰撞下，走向高阶思维。组织这样的数学活动更能帮助学生在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想与方法，获得广泛的数学活动经验。教师还可以根据学生思维水平的差异性，设计个性化的有针对性的训练，使学生思维进阶。

二、语义表征，高阶计算思维的具体化

一般来说 ，学生借助实物和具体物的动作表征进行思维活动后，教师都会让学生介绍自己是怎么做的，通过组织语言表达本质，这就是语义表征。教学中，教师可以引领学生将动作表征和语义表征相结合让数学思维具体化，使思维进阶。

再结合刚刚“9+几”这一课的课例，学生将盒子外面的苹果放进盒子里，这时让学生说说为什么这样做。学生说出因为十加几我们学过了，先想办法找到“十”，就好算了。学生可视化的思维结合自己的语言变得更加具体，发展出了一个问题解决不了转化成另一个学过的问题再解决的转化思想。这样的数学思维活动是宝贵的，两种表征相结合，使思维层次变高。在摆小棒解决“9+4”时，就可以要求小朋友们边摆边说：“4分成1和3，9加1等于10，10加3等于13。”这时学生思维用动作和语义同时表征，强化他们对9加几算理的理解。接著让学生收起小棒 ，同桌之间互相交流刚才摆的情况 ，学生借助刚才的操作进行数学思维和口语表述 ，其数学思维通过语义表征具体化。今后在解决同类型问题时可以在脑海中操作，然后借助语言表达，具象自己的计算思维，实现计算思维的高阶化。这时再让学生操作计数器，学生们的语义表征就更多样化了，相信这是每位数学老师都希望达到的课堂效果。

借助工具解决问题的确很简单，但是把操作影像留在脑海中，并利用其去解决同类型的问题，不是那么容易，需要有高阶的思维。语言是人类沟通交流的工具，要想将自己的想法、见解表现出来，不可能每次手边都有合适的工具将自己的想法形象的动作表征出来，这时就需要借助语言系统来补充表达。语义表征既能够丰富思维的过程，又具有高度概括的特点，能将数学中的规律美表现得淋漓尽致。

三、符号表征，高阶计算思维的抽象化

“符号意识”主要是指能够理解并运用符号表示数、数量关系和变化规律，知道使用符号可以进行一般性的运算和推理，建立符号意识有助于学生理解符号的使用是数学表达和进行数学思考的重要形式。随着数学学习的不断深入，数学符号从文字中不断地分离，形成抽象的数学符号语言。学生直接借助符号进行内在的思维活动，属于高层次思维水平，我们通常称之为 “符号性表征”水平。

例如，低年级学生在认识了0～5以后，教材就引入了“>”“<”和“=”这样的符号，利用一一对应这样的方法去比较大小，体现了对应的思想。遇到5个三角形和3个圆片比较，学生先一一对应摆一摆，然后说一说，最后用符号表示出“5>3”。这为后面学习减法奠定基础。跟踪发现学生们把被减数和减数交换位置的情况明显减少，说明先通过动作表征到语义表征最后到符号表征，将数学中对应思想逐步呈现，最后的符号表征将思维抽象成一个数学表达式，不仅体现数学的简洁之美，还能使学生抽象出数学的本质内涵。在“分与合”的教学中，学生们更是把先摆小棒的动作表征和语义表征相结合，最后用符号表征抽象出分合式，进而抽象理解10以内加减法算理。在“9加几”这节课中，通过动作表征和语义表征计算思维的方式，学生的学习更加深入了。学生学会用符号表征列出算式后，再遇到算式时就会在脑海中形成影像演算抽象出方法，体会十进制，抽象出凑十法的通用内涵，最终给出答案。这才是真正的高阶计算思维。数学思维从图像性表征水平走向符号性表征水平，完善了数学语言的表征，数学符号表征具有准确性、简约性和高度抽象性的特点，体现数学学科的特质。

普通思维可视化注重从生活到数学， 从现实情境到数学体系，而高阶思维是数学体系内部的变换与重组。但是在高阶思维的指引下， 学生的发展程度是不同的。动作表征，让思维通过学生的动手操作可见。动作表征和语义表征相结合使高阶思维被学生具体表达出来。能通过符号表征数量关系，建立数学模型，说明学生的思维得到了更高的发展，思维达到抽象层次。

教学中， 教师应该要整合融通， 既要关注普通思维的发展， 也要关注高阶思维的发展。在小学阶段，如果教师在数学教学中仅提供符号化、形式化的抽象表征，基础差的学生容易因为难以理解数学知识的抽象性，而对数学学习感到困难，甚至失去学好数学的信心。但如果在教学中巧用数学多元表征，利用不同表征可以互相补充和转换的作用，能让学生从不同的角度认识数学对象，从而深刻理解数学概念和原理，真正实现高阶思维的发展。