列车风激励下高铁声屏障连接螺栓经时松弛研究

卫 星，刘铭扬，温宗意，胡 喆，肖 林

(1.西南交通大学 土木工程学院，成都 610031；2.中铁第四勘察设计院集团有限公司，武汉 430000)

螺栓连接由于其施工速度快、便于维护的优势广泛应用于钢结构工程中，高速铁路声屏障支撑钢结构框架多采用螺栓连接。高速铁路声屏障受通行高速列车的列车风反复激励，螺栓预紧力将逐渐丧失，造成螺栓连接失效，影响声屏障耐久性。因此研究列车风激励下高速铁路声屏障连接螺栓松弛机理有重要意义。

螺栓连接的松弛原理及防松设计方面已有大量研究成果。王崴等[1]通过建立有限元模型，研究横向激励作用下螺栓松弛的影响因素，包括激励幅值、初始预紧力及结合面摩擦因数。侯世远[2]研究了松动初期预紧力下降的原因、影响因素及松动过程中接触状态的变化，并解释了温度引起的螺纹塑性变形及蠕变现象。邬杰等[3]通过有限元分析并结合试验，提出了基于预紧力、横向力、螺纹面摩擦因数的旋转松动刚度拟合关系式和线性的松动寿命预测函数。李海江等[4]通过试验研究了横向振动下预紧力衰减规律，认为松动初期预紧力与横向振动次数之间满足双指数函数关系。王灿等[5]通过理论分析结合图像处理技术研究了螺纹力学传递规律并提出了再次紧固的工艺。刘检华等[6]通过建立有限元模型并结合试验，研究了振动条件下楔形垫圈的防松性能。赵建平等[7]通过试验研究输电塔架联结螺栓在横向振动下的松动机理并使用电子显微镜观测螺纹啮合面磨损状况。Liu等[8]通过试验研究不同涂层对松动性能的影响。Zhang等[9]通过试验及建立有限元模型研究松动中螺纹磨损情况。何竞飞等[10]建立有限元模型研究预紧力和螺母旋转松动量随交变横向载荷变化的规律。杨广雪等[11]建立有限元模型研究一种新型防松螺母的防松机理。张维维[12]研究了电站高温螺栓松弛力学行为，建立了基于蠕变机理的应力松弛力学模型。Yang等[13]通过理论分析并结合试验，研究了横向荷载下自松弛的影响因素，计算了防止紧固件自松弛所需的最小预紧力。吴涛[15]建立有限元模型研究变牙型螺纹联接和普通螺纹联接的各圈螺纹处轴向力和法向力分布规律。Zhang等[16-17]建立有限元模型并设计试验分别研究了螺栓连接松弛第一和第二阶段的机理。赵登峰等[18]通过理论分析配合试验研究振动环境中螺栓连接松动过程的动力学响应特性。Pai等[19-20]通过有限元计算并设计试验研究动态剪切载荷导致的固定件松动，并做了相应理论分析。

上述研究主要集中在螺栓连接松弛机理方面，为使螺栓出现明显松弛，通常施加较大横向位移激励，实际环境中几乎不会出现。在确定荷载谱反复作用下，研究螺栓松弛程度与作用时间的关系对防松设计、加固维护有更重要意义。另外，同直径螺栓有多种螺距规格，涉及不同螺距对松弛程度影响的研究较少。本文通过建立考虑螺纹螺旋效应的三维螺栓连接有限元模型，在既有成果基础上重点研究不同横向激励幅值、初始预紧力及螺纹螺距对松弛程度的影响，并提出一种简易方法预测确定荷载谱下螺栓松弛程度。

1 有限元仿真分析

1.1 声屏障整体建模

某运行时速350 km/h双线高速铁路采用近轨侧覆盖吸声板封闭远轨侧开放形式声屏障。采用Midas Civil建立声屏障整体模型，纵向长度取梁体伸缩缝间距20 m，铁路桥梁体、立柱、连接系檩条采用梁单元模拟，铝合金吸声板采用板单元模拟。实际结构中吸声板横桥向通过橡胶支座与立柱连接，建模时采用3 500 N/mm弹性连接模拟。立柱单元底部与铁路桥梁单元固结，在铁路梁两端建立简支约束。声屏障整体模型如图1和图2所示。

图1 声屏障结构示意图

图2 单节段连接檩条及吸声板示意图

列车通过时产生的风压荷载直接作用于声屏障上，参照罗云柯[21]风压计算结果，将风压以节点动力荷载形式施加于声屏障上进行时程分析。由于连接系檩条通过螺栓传力给立柱，螺栓所受剪力主要来自檩条轴力，因此可通过檩条轴力最大处确定螺栓最不利位置。根据加载列车风压后结构计算结果，提取所有檩条轴力，如图3所示。

图3 脉动风压作用下声屏障檩条轴力图

由檩条轴力分布可知远轨侧顶部立柱弯折处檩条有最大轴力，提取此位置檩条轴力时程作为该处檩条连接螺栓所承受的横向外荷载，如图 4所示。

图4 最不利位置螺栓横向荷载随时间变化曲线

1.2 螺栓精细建模

檩条连接位置细部构造为方钢管檩条通过螺栓连接于焊接在立柱上的角钢，两颗螺栓夹持角钢和方钢管管壁，檩条通过螺栓传力给立柱，如图 5所示。

图5 檩条连接细部构造

针对一颗螺栓按其三维实际结构建立精细有限元模型，用两块板件代替螺栓夹持的角钢一肢和檩条钢管下管壁。采用ANSYS 19.0有限元程序，有限元模型如图6～图9所示。模型几何尺寸为：公称直径D=10 mm，螺距p=1.5 mm，齿形角60°，螺栓头直径S=16 mm，螺栓头高dw=6.4 mm，螺母厚k1=8 mm。两个加持板件均为40 mm×40 mm×8 mm，夹持板件孔壁与栓杆间孔隙δ=0.5 mm。模型材料属性为：螺栓材料为8.8级高强钢，屈服强度σs1=640 MPa，弹模E1=200 GPa，泊松比v1=0.3；夹持板件材料为Q235钢，屈服强度σs2=235 MPa，弹模E2=200 GPa，泊松比v2=0.3；计算时考虑材料弹塑性影响，采用理想弹塑性本构关系，弹性阶段弹模为200 GPa，屈服后弹模为0。

图6 螺栓连接整体模型

图7 夹持板

图8 螺杆

图9 螺母

引入夹持板件的目的是模拟被连接构件，同时方便施加螺栓预紧力和横向激励。坐标系设置为以螺杆轴向为Z轴，平行于夹持板件一边为X轴，与之垂直方向为Y轴，如图 7所示。

模型中采用能较好适应曲面形状和模拟滑移的3D8节点CONTRACT174单元、TARGET170单元建立柔性面-面接触对，分别在栓头-夹持件承压面、夹持件间承压面、螺母-夹持件承压面、螺纹啮合面建立接触。对接触单元设置KEYOPT(5)=3进行自动降低侵入及闭合间隙，接触算法使用增广拉格朗日算法，各接触面材料摩擦因数均设为0.15。

实际结构中通过拧紧螺母对螺栓施加预紧力，本次研究中通过降温模拟该作用。设置螺栓及夹持板件的线膨胀系数α1=α2=1.2×10-5，对螺杆区域降温，螺杆轴向缩短，挤压夹持板件，夹持板件轴向刚度较大不易变形，螺杆受到反作用拉力，达到预紧效果。提取螺杆中部截面轴向应力对面积积分，可得螺杆轴向内力，即螺栓预紧力。固定下夹持板侧面，施加预紧力22 kN，预紧后螺纹应力如图10所示。

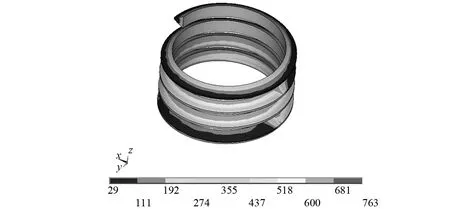
图10 螺杆螺纹Mises应力

将下夹持板侧面固结，上夹持板侧面施加横向荷载，如图 11所示。第一荷载步降温，以螺杆中间截面合力达到预期预紧力为标准；第二荷载步起施加交变荷载。交变荷载施加模式为0→F→0→-F→0，如图 12所示，共加载10周期。

图11 约束及横向荷载示意图

图12 周期横向荷载施加模式

2 螺栓松弛速率影响因素

螺栓初始预紧力下降量可反应松弛程度，为方便表述，将单周期横向荷载作用下螺栓预紧力平均下降量定义为松弛速率，单位为N。

2.1 横向力振幅

为考虑不同横向力幅值对螺栓松弛程度的影响，保持初始预紧力22 kN不变，分别施加幅值为500 N，1 000 N，1 500 N，2 000 N的周期横向力，观察预紧力损失。

由图13所示，在幅值为1 000 N的周期横向力作用下，螺栓预紧力呈现周期波动趋势，正向加载时预紧力增大，反向加载时预紧力减小，卸载时基本恢复初始值，每周期预紧力减少量可代表松弛速率。比较不同横向力幅值，如图14所示，预紧力下降基本呈线性，斜率可反应松弛速率，横向力幅值越大，剩余预紧力下降越快。图 15显示随横向力幅值增大，松弛速率非线性增大，指数函数可较好拟合变化趋势。

图13 每荷载步剩余预紧力变化曲线

图14 每周期剩余预紧力变化曲线

图15 不同横向力幅值相应松弛速率

2.2 初始预紧力

初始预紧力大小对螺栓松弛快慢有重要影响，为探究不同初始预紧力作用下螺栓松弛程度，保持横向力幅值为1 000 N不变，施加不同初始预紧力，观察预紧力减小程度。

随着预紧力改变，松弛速率非线性变化，较大和较小的初始预紧力均有较大的松弛速率。初始预紧力在14～20 kN区间时，松弛速率处于较低水平；低于14 kN及高于20 kN时，松弛速率均呈快速增大趋势。较大初始预紧力螺纹啮合处应力较大，容易进入塑性，而塑性变形的累计引起第一阶段松弛；较小初始预紧力导致界面摩檫力小，螺纹啮合处变形较大，同样容易造成塑性变形累计。图 16显示随初始预紧力的变化，松弛速率非线性变化，二次函数可较好拟合变化趋势。

图16 不同初始预紧力相应松弛速率

2.3 螺纹螺距

对M10螺栓常用螺纹螺距P=1.5 mm，P=1.25 mm分别建模，施加相同初始预紧力22 kN，幅值分别为500 N，1 000 N，1 500 N，2 000 N的周期横向力观察剩余预紧力变化情况，结果如图 17所示。随作用周期增加，两种螺距螺栓模型初始预紧力皆缓慢下降，螺距P=1.25 mm螺栓模型下降更快。图18显示，随周期横向力幅值增大，两种螺距螺栓松弛速率皆非线性增大，相同幅值周期横向力作用下螺距P=1.25 mm螺栓松弛速率大于螺距P=1.5 mm，横向力幅值为1 000 N时前者为后者的5.2倍，横向力幅值为2 000 N时为2.4倍。可知，大螺距螺栓较不易松弛。

图17 每周期剩余预紧力变化曲线

图18 不同螺纹螺距相应松弛速率

3 松弛程度预测

通过第1章、第2章所述计算方法，给定螺栓型号、初始预紧力，可得到某个横向荷载幅值对应松弛速率。但工程中声屏障檩条螺栓主要承受如图 4所示的连续荷载，若按该实际荷载历程加载，计算代价大且不具有普遍性。借鉴疲劳线性累计理论以及积分的思想，引入部分假设：认为连续荷载谱作用可分解为单周期作用的累加，两者所致的螺栓松弛程度相同。将连续荷载谱分解为单周期作用，按幅值分类，确定了螺栓型号、初始预紧力、外荷载幅值则较容易通过数值模拟获得某个幅值横向力作用一周期螺栓预紧力的下降量。将连续荷载谱中每个单周期作用对应的预紧力下降量累加可得该连续荷载谱作用一次所致预紧力下降量。这样，统计了螺栓服役期所经历的该荷载谱次数可计算预紧力随时间变化情况。

若横向力幅值介于500 N，1 000 N，1 500 N，2 000 N之间，其相应松弛速率通过线性插值得到。图 4所示荷载谱中出现过的所有横向力幅值(大于50 N)及其对应松弛速率如表1所示。

表1 单次列车通过引起的螺栓松弛损失计算

表 1中一次列车通过引起的松弛损失由各单周期作用对应损失累加得到。给定每天预计过车数量可得所求松弛程度(预紧力下降30%)所历经天数。考虑不同预紧力下，即使横向力幅值相同，单周期作用下螺栓预紧力下降值不同，建模时分别计算在22 kN，20 kN，18 kN，16 kN，14 kN，12 kN初始预紧力下，相同横向力幅值作用一周期的预紧力下降值。按每2 kN预紧力下降量分段考虑，每段内采用相同松弛速率计算。预紧力在20～22 kN内时，每周期横向力作用预紧力下降量按22 kN预紧力的计算结果近似替代，18～20 kN的相同幅值每周期横向力作用预紧力下降量按20 kN预紧力计算结果近似替代，得到各段预紧力下降所需天数。

对于承受类似图 4所示连续荷载谱的螺栓，将其承受的连续荷载谱分解为常幅横向荷载单周期作用与相应作用次数的组合，认为不同幅值交变荷载单独作用引起的松弛程度可线性累计，且考虑松弛速率随剩余预紧力下降的变化，则每段预紧力损失所经时间可计算得到。计算思路可表示为

Fre=F0·(1-∑niki)

(1)

式中：Fre为剩余预紧力；F0为初始预紧力；ni为第i个横向力幅值作用次数；ki为第i个横向力幅值对应松弛程度。

表2中列出了每段预紧力损失所历经时间，预测该声屏障立柱顶部位置檩条连接螺栓预紧力损失30%时间为3 926 d，即10.8 a。

表2 松弛损失预测

4 结 论

本文用有限元方法对周期横向剪切荷载作用下高速铁路声屏障连接螺栓的松弛问题进行仿真，重点研究横向荷载幅值、初始预紧力、螺纹螺距对松弛的影响，并通过一种简易方法尝试对确定荷载谱长期作用下螺栓松弛程度进行预测，得出以下结论：

(1)相同预紧力情况下，螺栓松弛速率与横向荷载幅值近似成指数函数关系。

(2)不同预紧力情况下，松弛速率随预紧力非线性变化，二次函数能较好预测趋势，较大和较小的初始预紧力均有较大的松弛速率。

(3)小螺距螺栓松弛更易发生，在初始预紧力及所受横向力幅值相同条件下小螺距螺栓松弛速率均高于大螺距螺栓。

(4)提出一种简易方法根据荷载谱及作用次数预测螺栓松弛寿命，推算维护时间，结果可供声屏障检测养护参考。