基于非光滑系统的局域共振声子晶体结构动态特性研究

何 超，高海峰，徐慧东，李志强

(太原理工大学 机械与运载工程学院，太原 030024)

低频振动和噪音的存在与长期工作生活在周围的人体内脏固有频率接近，产生的共振严重影响人体健康。而且在交通运输、航空航天以及精密加工等领域产生不利影响，造成了大量的经济损失，由此低频减振降噪显得尤为重要。声子晶体所具有的带隙特性使其在减振降噪方面的应用得到重视。早在二十世纪七十年代，人们就开始了对弹性波在层状介质中的传播进行研究[1]。在1993年，Kushwaha等[2]首次提出了声子晶体概念，并利用平面波展开法计算了弹性波带隙。1995年，Martinez-Sala等[3]通过声学特性试验对雕塑“流动的旋律”进行研究，第一次在试验中得到声波带隙。之后2000年，Liu等[4]在《Science》杂志上首次提出声子晶体局域共振带隙机理，制造出的三维三组元周期性复合材料，成功通过试验验证了“小尺寸控制大波长”，为局域共振型声子晶体在低频减振降噪领域的发展奠定了基础。局域共振型声子晶体这种周期复合结构在特定频率的弹性波激励下，各个散射体产生共振并与弹性波相互作用抑制其传播，由此产生了局域共振带隙[5]。根据局域共振声子晶体带隙的特性，在各个领域有着广泛的应用。由于其频率可设计、尺寸小、针对性强等特点，为精密加工、精密仪器等提供一定频率范围内的无振动工作环境。声子晶体也常用于声呐、医学超声探测成像等领域。在潜艇的消声瓦等军工方面也有广阔的应用前景。

到目前为止，主要的研究都是围绕局域共振型声子晶体的线性特性展开的。基于局域共振原理设计具有等效负质量密度、负折射特性的声子晶体，可以产生高效低频声吸收或隔离、声透射等现象，广泛应用于生产生活等各个方面[6-8]。尽管局域共振型声子晶体在低频抑振方面有着突出的表现，但是在宽频抑振方面有一定的局限性。因此非线性系统的引入可以改变带隙对系统线性特性的依赖性，从机理上对带隙特性产生影响。1955 年，Fermi等[9-10]研究了含有非线性项的64粒子的一维动力系统，后人将这一离散结构称为 FPU问题,对该问题的进一步研究极大地推动了非线性领域的发展。国防科技大学智能科学学院振动与噪声控制团队在非线性声学超材料低频宽带减振特性的研究上取得重要进展[11-16]探究了周期结构中的非线性波动与振动特性及新机理—混沌带，揭示了低频宽带高效抑振机制。目前，大量的工作围绕非线性周期结构的色散关系开展。研究发现带隙频域和带宽可以通过调整非线性的强度来调控, 并且随着激励幅值的增加，带隙频率和色散曲线向高频移动，带隙宽度增加[17]。2013年Donahue等[18]用颗粒晶体设计了用于水下声聚焦和成像的非线性声透镜结构，并成功通过试验实现。2017年，Ciampa等[19]提出的非线性弹性波传感声子晶体波导换能器，成功地使超声设备产生的二次谐波产生衰减，从而证明了非线性声子晶体在超声材料损伤检测中的广泛应用潜力。近期Khobragade等[20]的研究表明，利用非线性声学共振器，可以直接可靠地读出生物受体介质的复杂样本中整个营养细菌的结合。

本文的研究基于一维扭转局域共振型声子晶体[21]，利用机械结构在局域共振声子晶体的基础上构建了非线性声子晶体结构。利用传递矩阵法验证线性带隙，并通过扭振衰减试验验证了线性带隙的存在。运用单自由度非光滑振动碰撞理论，通过数值仿真对单个振子运动微分方程的稳态解进行分析研究，说明了振子在多个低频频域内存在分岔和混沌等非线性现象。在上述结构基础上加入非线性机构并对该新结构进行扭转减振试验分析，进一步说明多振子叠加产生混沌带隙的机理。并与在同强度宽频激励下的线性带隙进行对比分析，表明混沌带隙在少量振子周期排列的情况下对包括10 Hz在内多个低频频域内的振动都有显著的抑制效果。

1 声子晶体结构的构建

局域共振声子晶体扭转结构由作为元胞基体结构的均质轴系和其上周期排列的一种新型扭转局域共振单元组成，如图1所示。该单元为通过轴承(16004型)黏接在轴系上的圆盘形质量块及弹簧等构成的元胞，局域共振单元间距为a(晶格常数)，轴承的内圈和外圈分别与轴的外表面和金属圆盘的内表面黏结，如图2所示。轴的半径为R0,轴承外圈内圆半径为R1，振子内圈半径为R2，振子外圈半径为R3，振子厚度(即轴向长度)为L。两组弹簧机构对称安装，以使其对轴的扭矩抵消，其距轴心的距离为Rk,每组弹簧的两端分别固接在轴系以及质量盘上，弹簧刚度为ks。图2中强非线性碰撞体系由质量盘上固接弹簧机构的碰撞杆和固接在轴系上一根独立于元胞的立柱构成，当扭振振幅等于间隙时，两个接触点从分离状态过渡到接触状态时会发生碰撞，碰撞前后振子的角速度产生突变，从而产生强非线性。

图1 轴系示意图

图2 局域共振单元示意图

2 带隙形成机理

2.1 局域共振带隙

本文的如图1中给出的扭转局域共振单元，在未达到碰撞非线性的条件时，通过传递矩阵法[22]计算扭转减振结构的色散关系，该局域共振单元，在扭转波激励下绕轴线扭转振动，波动方程为

(1)

局域共振声子晶体带隙由元胞结构决定，在无限周期结构中计算该元胞带隙，第n个元胞的解可以写成

θ(xn,t)=T(t)Θ(xn)=

eiωt[Ansin(qxn)+Bncos(qxn)]

(2)

式中:xn=x-na;ω为角频率,q=ω/c为扭转波的波数。假设第n个局域共振结构中金属盘的扭转位移为

φn(t)=Vneiωt

(3)

式中，Vn为第n个振子的振幅。对于第n个振子的惯量矩，根据力矩平衡得

(4)

将式(2)和式(3)代入式(4)中得到

(5)

由第n-1个晶胞和第n个晶胞之间的位移连续和扭转连续得到

Bn=An-1sin(qa)+Bn-1cos(qa)

(6)

An+FBn=An-1cos(qa)-Bn-1sin(qa)

(7)

式中，F=ω2IK/(G0JtqK-Iω2)。将式(6)及式(7)写成矩阵形式为

Ψn=TΨn-1

(8)

式中:Ψn=[An,Bn]T；T为传递矩阵。

T=

(9)

由|T-eikaI|=0可以求解到解析的色散关系为

(10)

式中，k为x方向的Bloch波数。对于任意给定的频率ω，利用式(10)可以求得对应的k值，即可获得局域共振声子晶体扭转线性带隙特性。

为了研究分析该结构带隙特性，具体验证该声子晶体的线性带隙结构，取基体材料为有机玻璃，密度ρ0为1 142 kg/m3,剪切模量G0为0.072×1010Pa。金属圆盘材料为硬质铝合金，密度ρ1为2 800 kg/m3, 轴承外圈材料为轴承钢，密度ρ2为7 810 kg/m3。结合表1试验结构参数及材料参数，角频率ω取0～560π rad/s，通过传递矩阵带隙计算方法计算得声子晶体局域共振扭转带隙结构，如图3所示。由图3可知，该结构可在12.4～235.3 Hz(24.8π～470.6π rad/s)产生局域共振线性带隙。

表1 试验结构参数

图3 带隙结构图

2.2 混沌带隙

该非光滑系统混沌带隙的研究分析基于单自由度振动碰撞理论，两个物体在相互接触时，在接触点产生非线性的力与变形，该强非线性行为使系统产生分岔、混沌等非线性现象。如图1所示结构，只考虑圆盘振子的扭转运动，振子通过线性弹簧与轴体上连杆连接，并且轴体受到简谐激振力的作用。随着激振力幅值的增大，当质量块的相对角位移θ(t)等于间隙θ0时，质块将与刚性约束碰撞，速度方向发生改变。在弹簧作用下又以碰撞后新的初值运动，然后再次与约束碰撞，如此反复；假设碰撞过程中的能量损失由碰撞恢复系数r确定，碰撞持续时间略去不计。

轴体做简谐运动

θ(t)=θgcos(Ωt)

(11)

(12)

式中：θg为轴体的扭振振幅；Xg，Rg分别为激振器振幅和连接处据轴心的距离。

在相邻两次碰撞之间，单个振子振动的运动微分方程为

(13)

式中：Fg=IΩ2θg；I为振子转动惯量；C为系统阻尼系数；K为系统扭转等效刚度系数；θ(t)为圆盘与轴体的相对转角。

由碰撞动量守恒定律，碰撞恢复系数r的定义，得碰撞瞬时方程为

(14)

根据微分方程的相关理论，上述式(13)运动微分方程的通解可表示为

θ(t)=e-ζωnt[X1cos(ωdt)+X2sin(ωdt)]+

Xrcos(Ωt-φ)

(15)

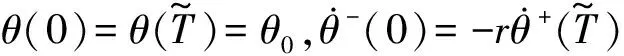
利用数值仿真求解上述非光滑碰撞振子的运动微分方程，针对该非光滑扭振碰撞振子，采取碰撞截面作为Poincaré截面。计算时边界条件中涉及的碰撞间隙取0，阻尼C及碰撞恢复系数r在3.2节试验参数估计中给出。通过该截面方法对上述微分方程的稳态解进行取值分析，得到单自由度碰撞振动系统全局分岔图，如图4所示。图4(a)～图4(d)四幅图说明在多个频率范围内的非线性情况，在这些频域内规律的出现小范围的分岔和混沌现象。分岔是由稳定解失去稳定性之后产生的一种非线性现象，这将伴随不稳定解的出现，而存在不稳定的解是出现混沌的必要条件，不稳定的周期解和稳定性交替变化的频带会导致混沌波的产生。因此本文基于一起出现分岔和混沌的分岔图进一步来验证试验结果。图4(e)为140 Hz附近范围内的局部分岔图，也表明该区域有着丰富的分岔和混沌现象。

图4 速度分岔图

3 试验装置及参数

3.1 试验装置

为了对该非光滑局域共振系统进行试验分析，基于上述结构参数和材料参数制作了如图5所示的试验结构。轴体通过两个支座固定在试验台上，振子等间距的周期排列固定在轴体上。在基体一端施加0～300 Hz轴周向简谐激励，使用激光位移传感器分别在轴的两端拾取扭转位移激励和响应信号。试验流程及仪器如图6所示。通过傅里叶变换将时域信号转变为频域信号，通过振幅频谱图对该系统线性及非线性减振特性进行研究分析。

1.简谐激励；2.激光位移传感器；3.轴的左端；4.振子；5.轴体；6.轴的右端；7.支座。

图6 试验流程图

3.2 试验参数

图7 弹簧刚度(k=338 N/m)

图8 振子脉冲响应

图9 离散傅里叶变换的幅度(峰值处频率为10.49 Hz)

图10 单次碰撞位移曲线

4 试验数据分析与数值仿真对比

通过试验得到的线性振幅频谱图，如图11所示。阴影区域为通过传递矩阵法得到的带隙计算结果所在频率区域。

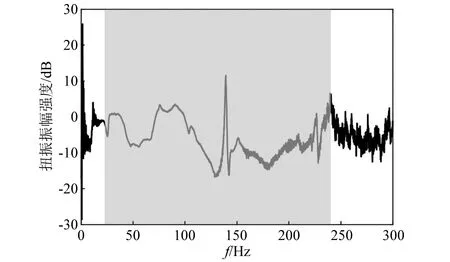
图11 线性振幅频谱图

从图11中可以看出，从12 Hz附近振幅开始出现衰减趋势，由于带隙计算时按照无限周期结构计算，而试验所用结构仅安装了五个局域共振单元，因此会在理论计算带隙内存在一些特征频率[23]，在这些特征频率附近振幅强度衰减较弱。在减振效果明显的频域范围内，振幅强度降低了10～15 dB。与数值计算结果对比可得，线性带隙试验结果基本符合计算预期结果。

在上述线性试验研究的结构基础上，由于碰撞机构的存在，使轴系在扭振时在特定频率内产生非线性现象从而形成混沌带隙。在同强度宽频激励下，得到非线性结构振幅频谱图如图12(a)中实线所示，在阴影区域A(15～45 Hz)、区域B(70～130 Hz)、区域C(148～180 Hz)三个频域范围以及140 Hz附近，振幅强度出现了剧烈衰减。对照图4速度分岔图进一步说明单个振子在这些频域内规律出现小范围分岔和混沌使系统产生混沌带隙。多个振子间相互耦合在局域共振带隙频域内激发不同频率的振动，使低频通带内共振峰数量增加，将能量分散在多个频率范围内，不仅抑制了低频振动，还拓宽了局域共振线性带隙。相对于线性带隙，该系统在同等外部激励条件下振幅强度降低了10～20 dB，对扭转振动的抑制作用明显强于线性带隙，弥补了线性结构在实际应用中振子数量较少而引起的抑振效果不明显的不足。

相对于线性带隙，混沌带隙有效地在更低频域内抑制振动。如图12(b)所示为更低频率的振幅频谱细节对比图，从图中可以得到在3～8 Hz的频率范围内，振幅强度从-5 dB附近最低衰减到了-20 dB以下，说明该结构在10 Hz以下的低频范围内无论线性还是非线性机构都可以有效抑制振动，尤其是非线性条件下混沌带隙范围内的振动强度衰减剧烈。

图12 线性与非线性振幅频谱对比图

5 结 论

(1)通过传递矩阵法对该扭转局域共振声子晶体结构的线性带隙进行计算，得到该周期结构可在12.4～235.3 Hz产生局域共振线性带隙，并设计加工周期扭振机械结构，通过对该结构进行扭转减振试验分析，对照前文传递矩阵法数值仿真结果，验证了该声子晶体结构的线性带隙。

(2)采用数值方法对包含非光滑系统的单个振子运动微分方程的稳态解进行分析研究，说明了振子在多个低频频域内存在分岔和混沌等非线性现象，解释了声子晶体结构混沌带隙产生机理。

(3)对含有非光滑系统振子的声子晶体结构进行扭转减振试验分析，通过试验验证了混沌带隙与单个振子非线性动力学特性之间的作用，并且可以看出混沌带隙与线性带隙叠加作用下不仅提高了抑振效果并且在线性带隙以外10 Hz以下产生了基于混沌带的抑振特性。