基于轻气炮加载的火工冲击环境模拟技术研究
2021-12-02赵宏达丁继锋郝志伟刘一志
赵宏达,孙 毅,丁继锋,郝志伟,刘 伟,王 熊,刘一志
(1.哈尔滨工业大学 航天学院,哈尔滨 150001;2.华中光电技术研究所,武汉 430200;3.北京空间飞行器总体设计部,北京 100094;4.太原理工大学 航空航天学院,太原 030600)
航天器火工冲击环境是搭载精密设备所经历的最为严酷的力学环境之一[1-3]。该冲击环境通常会造成精密设备出现损伤或故障,甚至引起航天任务的失败等严重后果[4-8]。因此,精密设备会在服役前进行地面冲击环境模拟试验以考核其抗冲击性能。然而,由于火工冲击环境具有高频、瞬态和高量级的特点,在实际冲击环境试验时往往需要反复调试以匹配冲击试验条件,缺乏有效理论指导。因此,深入开展火工冲击环境的模拟技术研究具有重要意义。
目前火工冲击环境考核试验主要通过真实火工品爆炸、机械撞击或电动振动台等方式进行[9]。采用真实的火工品爆炸激励是最直接、可靠的方法之一。Filippi等[10]采用火工品爆炸激励对冲击环境模拟技术进行了大量试验研究。在500多次火工冲击试验中重点研究了试验装置夹具类型、接触/非接触爆炸和火工品安装位置三个变量对冲击环境的影响。马斌捷等[11]采用该方法对仪器支架缓冲性能、电磁阀冲击、火箭舱段冲击等开展试验研究,取得了较好的效果。Zhao等[12]采用显式有限元程序LS-DYNA对双板式火工冲击环境模拟平台开展了数值仿真研究。火工品爆炸式加载机理和火工冲击环境相同且能够同时实现三个方向的冲击加载,但采用火工品进行试验会存在危险性和试验结果分散性较大等问题。机械撞击式主要利用摆锤或气炮等撞击谐振夹具从而激起具有多阶模态的谐振响应以模拟火工冲击环境。Kolaini等[13]提出了一种可调谐式谐振梁装置并指出调整谐振梁两侧的约束位置可以改变梁的基频,从而实现冲击响应谱拐点频率调节功能。该装置通过底部气炮子弹冲击谐振梁中部使其产生谐振响应实现对安装于谐振梁上部设备的冲击加载。Harris等[14]提出了一种谐振板式机械冲击激励装置。该装置利用摆锤下落撞击谐振板从而在谐振板上产生面内方向的冲击响应或者利用中间的气动撞击在谐振板上产生面外方向的冲击激励,实现对设备多方向的冲击考核功能。Velmurugan等[15]采用试验和数值的方法研究了复合材料谐振板在轻气炮子弹冲击加载下的火工冲击环境模拟技术。他们重点探究了响应板厚度、测点位置、子弹长度以及子弹速度等对响应板测点的影响。机械撞击式模拟方法具有良好的操控性和试验结果一致性,但产生的冲击环境受到装置参数等影响,谱型精确控制方面仍存在一定困难。电动振动台模拟是采用电动控制技术在振动台产生合成的冲击时域响应信号对试件进行加载。该方法具有优良的可控性和重复性以及低成本等优点。但是其缺点也是明显的,如受到振动台电机等技术限制,该方法在仍无法模拟高频冲击信号。除上述三种方法外,采用激光激励模拟火工冲击环境是近年来新兴起的一种技术。其主要原理是利用激光发生器产生高能激光脉冲作用于加载板结构的物质表面时产生瞬时热作用在固体表面产生热应力区,从而在物质内部产生应力波。2014年,Jang等[16-17]将激光激励技术应用于火工冲击环境模拟领域并在后续研究中将该方法用于复合材料板加载。王锡雄等[18-19]也对激光激励技术进行研究并发现激光激励冲击响应经过放大后与真实火工冲击响应的时频特性基本一致。激光脉冲加载技术受到能量限制其产生的冲击环境还无法达到火工冲击的高量水平,目前仍处于探索阶段。
综上所述,火工冲击环境模拟技术已经取得了一定进展,但同时各方法也存在相应不足。本文在机械撞击式的良好的操控性和结果一致性等优势的前提下重点对该方法的冲击环境谱型控制技术难点开展深入研究。首先,设计了一套基于轻气炮加载的多调节参数火工冲击环境模拟装置并对其一致性进行了试验验证。然后,对于该装置的可调节参数对谐振板上冲击环境的影响规律进行了不同工况下的冲击试验,包括不同气室压强、子弹长度以及连接杆的定位孔等工况。同时,结合数值仿真优势对不同调节参数的影响规律进一步开展分析。总结了相应的定量关系式或给出了定性影响结果。最后,通过一个算例对研究结果准确性和可靠性进行了验证。本文提出的冲击环境模拟装置和总结规律在一定范围内克服了机械撞击式模拟方法谱型控制的难题,可为提高航天工程中火工冲击试验效率提供参考。
1 装置设计及冲击试验
1.1 冲击环境模拟装置结构设计
根据与冲击源的距离及响应幅频特性,可以将火工冲击环境大致分为近场、中场和远场[20]。火工冲击在近场表现为冲击波效应,传递至远场结构时则表现为引起结构的谐振。一般精密设备大多布置在远场区域,因此,其火工冲击环境多表现为结构谐振响应。采用轻气炮加载的机械撞击式模拟方法能够激起设备安装板高阶的谐振响应,这与火工冲击环境的远场响应特性相类似。火工冲击环境模拟装置实物图,如图1所示。该装置主要包括加载板、谐振板、连接杆、设备样件以及加载装置等几部分组成。各部件参数如表1所示。其中,待测试设备样件底部进行挖槽处理以综合模拟设备安装于支架的情形。在加载板和谐振板上沿斜对角方向和与边平行方向分别设置有五个定位孔,用于调节连接杆的位置。该装置的调节参数有:气室压强(子弹速度)、子弹长度、连接杆定位孔位置等。该装置的基本原理是通过调节不同的参数以在谐振板上实现特定的冲击试验条件,从而完成对待测试设备的抗冲击性能考核。

图1 冲击环境模拟装置及待测试样件实物图

表1 冲击环境模拟装置参数
1.2 冲击环境模拟装置的冲击试验
冲击试验如图2(a)所示。试验前,模拟装置与待测试件样件通过四根柔性绳悬挂于试验支架上。除冲击环境模拟装置外,整个试验系统还包括轻气炮加载装置、加速度传感器、信号放大器和信号采集系统等几部分。冲击试验系统入射装置如图2(b)所示。子弹在气室内高压推力作用下沿炮管飞出,与入射杆之间强烈碰撞并产生具有高频、瞬态和高量级的特点的冲击波。冲击波经过入射杆、加载板和连接杆最终传递至谐振板,实现冲击环境加载。同时,子弹在冲击入射杆后反弹回炮管内部。为了进一步保障测试设备和人员的安全,在炮管与入射杆端部设计了保护罩等防护措施。

图2 冲击环境模拟试验实物图
加速度传感器的分布实物图和示意图分别如图3(a)和图3(b)所示。本试验中压电式加速度传感器的测量范围为30 000g,采样频率100 kHz。电荷放大器采用16通道DH5862,最大输入电荷量为106 PC,最大带宽为0.3 Hz~100.0 kHz。数据采集设备为DH5956动态信号测试分析系统。信号采集系统安装于计算机上,可以在软件中设置参数和捕获试验结果。数据采集完成后通过离散小波变换算法对试验数据进行高频滤波和低频趋势项去除等数据处理,从而避免高频噪声干扰和修正零漂现象。

图3 加速度传感器布置位置
良好的一致性是试验结果具有较高可信度的前提,在上述冲击试验平台重复三次冲击试验并基于S1测点响应进行一致性分析。三次试验中S1测点的加速度时域响应,如图4(a)所示。图中三次冲击试验在时域的响应波形相似且幅值相近,三条曲线基本接近,初步表明上述冲击试验平台具有良好的一致性。
冲击信号在时域一般表现为复杂震荡波形,从时域方面进行比较分析是非常困难和苛刻的。在工程实践中,普遍以冲击响应谱作为考核冲击强弱的指标。所谓冲击响应谱就是将时域响应信号加载至一系列不同固有频率的单自由度系统基底上,然后以固有频率为横坐标,对应固有频率下各单自由度系统响应最大值为纵坐标所作的一条频域曲线。冲击响应谱的计算方法详见文献[21]。将图4(a)三条时域响应曲线分别作冲击响应谱变换,如图4(b)所示。图中三条冲击响应谱的拐点频率和幅值基本吻合。三条曲线的最大偏差为在9 589 Hz频率处1 213g,为该处三次试验平均值的13.7%(约为1.1 dB)。分析研究表明上述冲击环境模拟平台具有良好的一致性,其系统误差远小于工程实际要求。
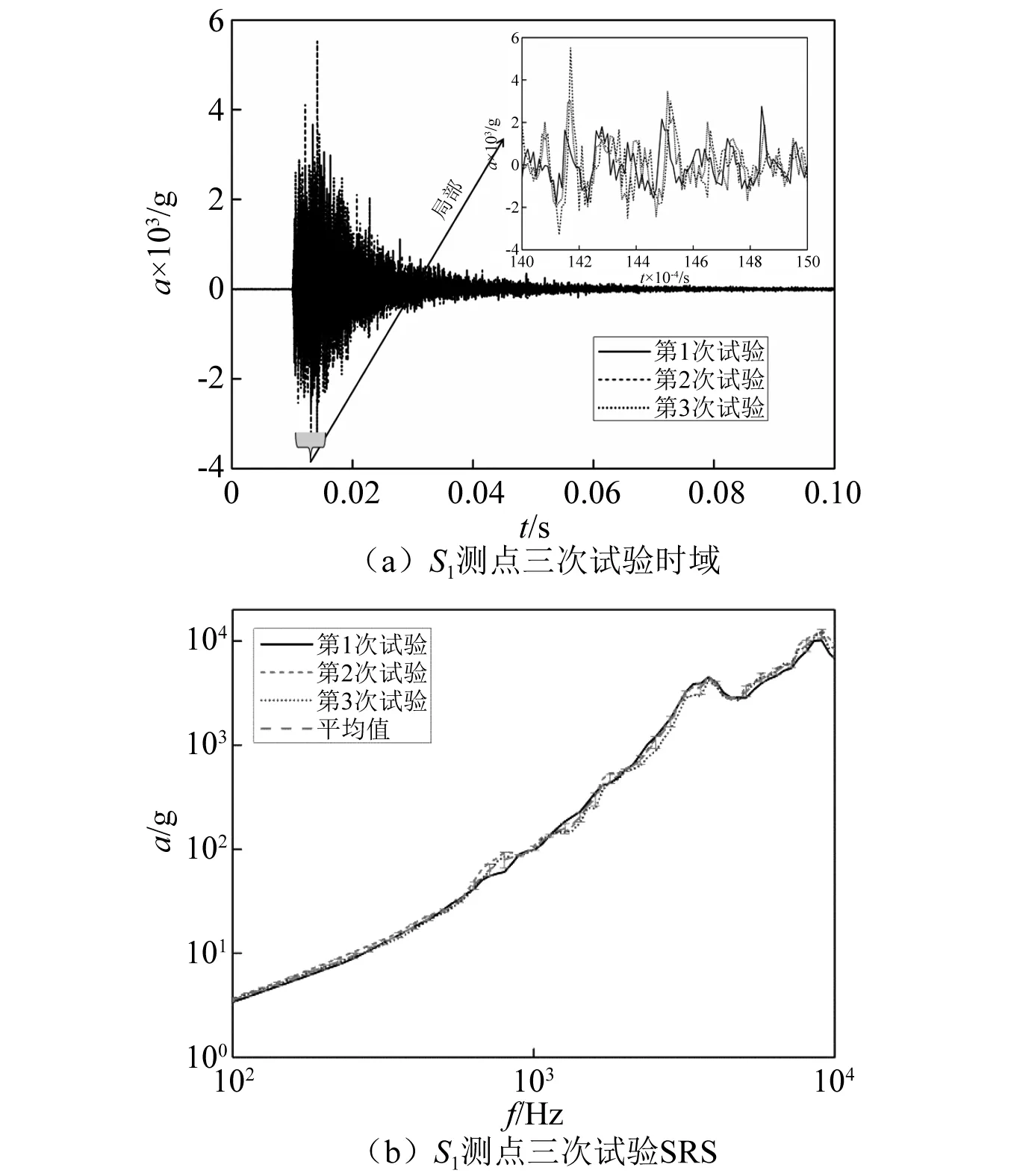
图4 S1测点三次试验时域结果和冲击响应谱频域对比
2 冲击环境影响因素及规律研究
2.1 冲击响应谱的三要素
工程中冲击环境试验条件普遍以冲击响应谱形式给出。标准的冲击试验条件如图5所示。从图5中可以看出,标准冲击响应谱主要包括低频斜率、拐点频率以及高频幅值三部分组成,称为冲击响应谱的三要素。冲击环境模拟技术的重点是研究冲击环境模拟装置中可调节参数对装置谐振板冲击响应谱三要素的影响规律,从而为冲击试验条件的快速实现提供技术支撑。

图5 冲击响应谱三要素
2.2 最高期望飞行环境
在实际冲击环境模拟测试中,根据待测试设备的种类、外形等的不同,安装点将会随之发生改变。同时,单个爆炸冲击事件所产生的谐振板上的响应往往会因为位置不同而存在差异。因此,需要将谐振板进行分区,使得在该区域内所有位置的响应基本保持一致。也就是说,在一个区域内所有位置的冲击响应谱可以用一个冲击响应谱表示,它包括了该区内大多数或所有位置的冲击响应谱值,这个响应谱就称为“最高期望飞行环境”(maximum expected flight environment,MEFE)。
最高期望飞行环境的计算包含以下两步:
步骤1将谐振板上冲击响应谱值相近的点进行分组,即分“区”;
步骤2在每个区内所有冲击响应谱值取一个保守的上限,称为“分区限”,它代表该区的最高期望飞行环境。
一个分区内各点的爆炸冲击的保守极限值可以有多种选择。最简单的方法是取该区内所有位置点的冲击响应谱的包络值作为最高期望飞行环境。但这种方法往往导致欠试验。目前使用较为广泛的一种方法是计算能够包络分区内至少95%以上部位的冲击响应谱值并具有50%置信系数的额定容差限,即所谓的P95/50。
对于服从高斯分布的随机变量其容差限通过简单计算可以得到。一般火工冲击造成的卫星结构响应在空间域内并不满足高斯分布,但是大量数据表明火工冲击响应的对数变量在空间近似服从高斯分布。因此,将冲击响应数据做如下变换
y=lgx
(1)
式中,x为在一个分区内响应在特定固有频率的冲击响应谱值。
变量x经上式转换后得到的变量y近似服从高斯分布。在特定分区内n个测点的值转换后的变量y的额定容差限的计算式为
(2)

(3)
式中,knβγ为额定容差因子。当β=0.95,γ=0.5时不同采样点所对应的k值,如表2所示。

表2 P95/50标准容差限的容许因子表
从以上推导可知原变量x的额定容差限由式(4)获得
Lx=10Ly
(4)
本文后期数据处理中将整个谐振板划分为一个分区以综合考虑各测点的影响。因此,测点数n取10,相应的容许因子knβγ的值为1.70。
2.3 气室压强的影响
试验首先探究了轻气炮气室压强对谐振板的冲击环境的影响规律。图6(a)和图6(b)分别为连接杆在定位孔“h1”和“h3”两种工况下,轻气炮压强从0.02 MPa逐渐增大至0.10 MPa时谐振板的MEFE曲线。由图可知不同气室压强工况下谐振板的MEFE曲线的线型基本一致。随着轻气炮气压从0.02 MPa增加至0.10 MPa,谐振板MEFE曲线的幅值也逐渐增大,但增速降低。此外,随着气室压强的变化,谐振板MEFE曲线主要表现为幅值的变化,线型基本保持不变。以上分析表明气室压强主要对谐振板的冲击环境的幅值起到重要影响,而对冲击响应谱的谱型,即冲击响应谱的拐点频率和低频斜率基本无影响。

图6 不同压强下谐振板的MEFE
为了进一步给出气室压强对谐振板的冲击环境峰值的定量影响规律,取图6中不同压强下各MEFE曲线的拐点频率所对应的峰值,分别如图7中方点及三角形点所示。由试验结果可以看出谐振板的最高期望飞行环境拐点峰值与轻气炮压强近似成二分一幂次方关系。因此,分别拟合得到连接杆定位孔为“h1”和“h3”两种工况下谐振板MEFE拐点峰值和气室压强关系为

图7 气室压强和谐振板MEFE峰值关系曲线
(5)
式中:Gh1和Gh3分别为当定位孔为“h1”和“h3”工况时谐振板MEFE曲线拐点峰值;p为气室压强。当冲击试验条件中的拐点峰值确定时,冲击环境模拟装置中轻气炮气室压强可由式(5)确定。
根据能量守恒定律可以推导得到气室压强p与子弹射出炮管时的速度v有[22]
(6)
式中:Sf为炮管内径对应面积或子弹横截面面积;Lf为炮管长度;m为子弹质量。
式(6)是基于子弹入射过程中气室压强始终为初始压强假设得到,事实上,在子弹入射过程中气室压强在逐渐减小。因此,将式(6)进行简单推导变换并引入修正系数α可得
(7)
式中:cf=1/(Sf·Lf)为所对应的炮管空腔的体积的倒数,对于特定的气炮装置其值为常数;系数α的值可以通过试验拟合或与数值结果对比分析得到。从式(7)可以看出气室压强与子弹射出炮管时的动能成正比。当气室压强一定时,子弹射出炮管的动能为定值,即输入到模拟装置的能量不变,与子弹的长度等参数无关。
为了进一步验证上述结论,更换长度为8 cm,10 cm,12 cm和20 cm的子弹设置气室压强均为0.05 MPa分别进行冲击试验。四种不同工况下谐振板的MEFE曲线,如图8所示。图中除子弹长度为20 cm工况下MEFE曲线在高频部分与其他有一定误差外,四条曲线基本吻合。这种现象可以作如下解释。相同材料的子弹在改变其长度的同时其质量也随之发生改变。当子弹质量增大时,在相同气室压强作用下,子弹飞出炮管时的速度减小,总动能不变。因此其在谐振板上引起的冲击环境的幅值亦不变。试验结果表明在气室压强一定的情况下子弹长度对冲击环境基本不会产生影响,与上述结论相一致。

图8 不同子弹长度下谐振板的MEFE
2.4 连接杆定位孔的影响
调整连接杆的定位孔并进行冲击试验,得到不同定位孔工况下谐振板上的MEFE曲线,如图9所示。图9(a)中当连接杆处于“h1”孔位时,MEFE曲线的拐点频率为3 500 Hz。当连接杆处于“h2”~“h5”孔位四种工况下各MEFE曲线差别不大,其拐点频率均约为1 600 Hz。此外,还可以看出第一种工况与后四组工况在低频斜率也存在明显差异。图9(b)中当连接杆水平向内移动,即处于“h6”~“h9”定位孔时谐振板MEFE与斜向移动具有相同规律。上述分析直观表明连接杆孔位会对谐振板的冲击环境的拐点频率和低频斜率产生影响。但是这种影响规律并未随着连杆孔位的变化呈现出递进的变化,而是表现为两种集中的状态。分析数据曲线发现在连杆处于“h1”孔位时谐振板的MEFE曲线在1 600 Hz频率点处存在一个小的“凸起”,该凸起的位置正好对应于其余四种工况的拐点频率处。因此,分析造成上述两级化的原因如下。在约1 600 Hz频率范围处正好对应于谐振板结构的某阶固有频率,在第一种工况约束条件下,该阶振型受到抑制,危险频率主要表现为3 500 Hz所对应的频率点。当约束条件改变时,1 600 Hz处的频率点受到激发,振型占据主导作用,表现为主要的危险点。

图9 不同定位孔连接工况下谐振板的MEFE曲线
2.5 加载板厚度的影响
本节基于数值方法探究了加载板厚度对冲击环境的影响规律。有限元模型几何尺寸与试验装置保持一致。考虑到模型的对称性以及节约计算时间和存储空间,只建立四分之一模型并在对称面施加对称约束。冲击环境模拟装置有限元模型,如图10所示。模型中所有单元类型均为3D Solid164单元,单元总数和节点总数分别为62 638和81 383。不同部件之间设置自动面面接触。模型建立完成后提交LS-DYNA solver进行求解,并在后处理中提取与试验加速度传感器相对应位置节点的加速度响应进行分析。
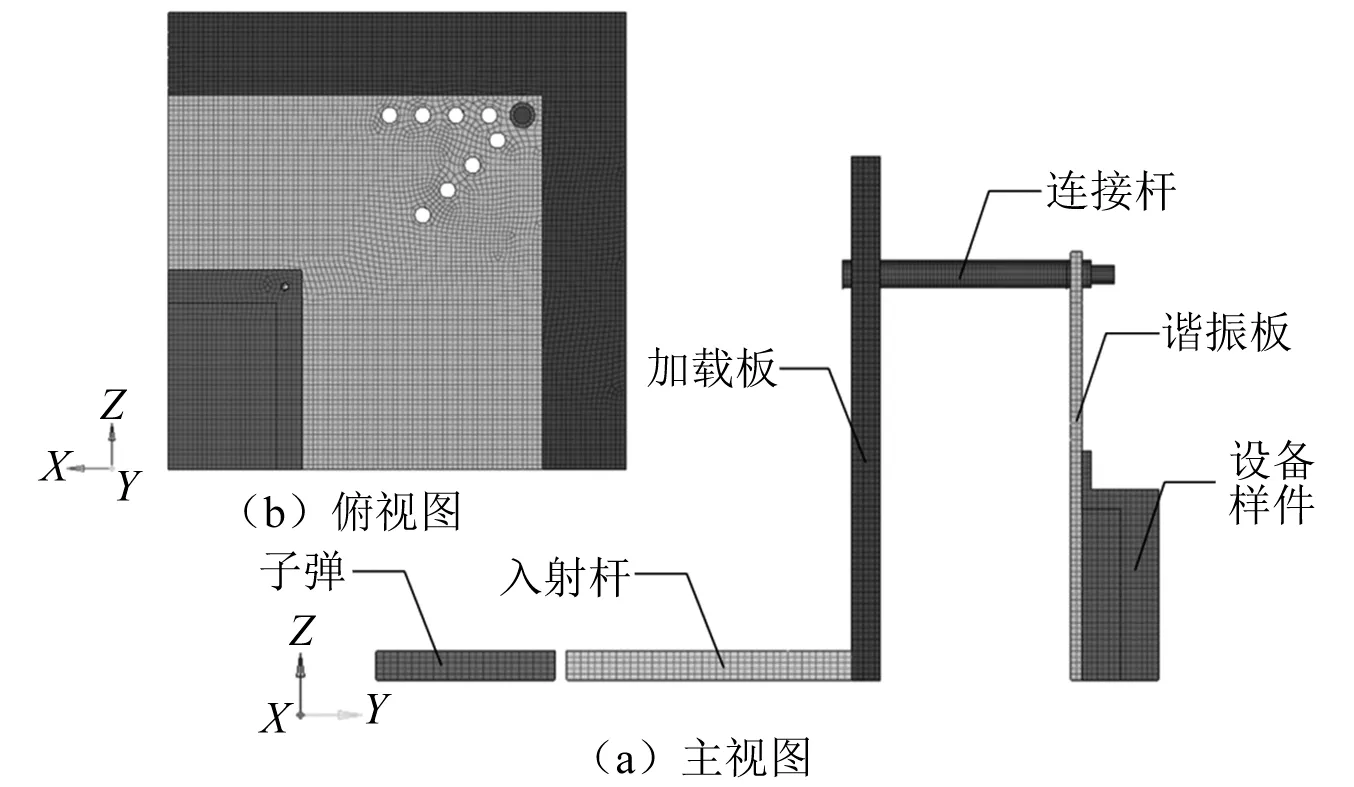
图10 冲击环境模拟装置的四分之一有限元模型
将有限元模型中子弹速度设为变量,调整模型中子弹速度分别进行数值求解。计算完成后,提取谐振板上与试验中传感器对应位置共十个节点的加速度冲击响应时域曲线并作冲击响应谱变换,求得其最高期望飞行环境与试验结果对比。图11(a)和图11(b)分别为当子弹入射速度为6 m/s时定位孔在“h1”和“h3”两种工况下谐振板的最高期望飞行环境与试验结果对比。图中两条曲线谱型基本一致,其中数值结果整体包络在试验结果的±3 dB范围内。进一步计算可知两条曲线的平均误差为1.627 dB,最大误差为5.415 dB位于4 794 Hz频率点处。分析表明冲击试验结果与数值结果之间存在较好的一致性,上述建立的火工冲击环境模拟装置有限元模型具有较高的精度。同时表明冲击试验中在0.06 MPa气压下12 cm子弹的入射速度约为6 m/s。

图11 试验结果和数值结果对比
加载板厚度在9 mm~17 mm内取不同值,并将连杆分别置于“h1”,“h3”和“h5”孔位进行数值仿真求解。各工况下谐振板上十个节点的最高期望飞行环境的拐点频率,如表3所示。从表3中分析可知,当连接杆的定位孔固定时,随着加载板厚度的逐渐减小,谐振板的MEFE拐点频率逐渐减低。这种现象的原因可以解释为加载板的固有频率随着厚度减小而减小。加载板上连接杆的位置对应于谐振板的激励点,激励点的输入信号中频率成分发生变化引起谐振板的MEFE拐点频率逐渐变化。同时,可以发现当连接杆定位孔由“h1”转为“h3”时,每种厚度工况下前者的拐点频率值均大于后者,这是由于连接杆的定位孔改变了谐振板的约束边界条件,该分析结果与2.4节中试验结果一致。
图12为表3中几种不同定位孔和加载板厚度组合工况下的谐振板的MEFE曲线。由图12可知,当连接杆定位孔或加载板厚度发生改变时,谐振板的MEFE曲线除拐点频率发生变化外,其低频斜率和拐点峰值也不尽相同。上述现象表明连接杆定位孔和加载板厚度对MEFE曲线的三要素的影响具有“一对多”的多参数耦合效应。本文将低频斜率定义为曲线起始频率至拐点频率范围内曲线上的点的斜率的平均值。计算表达式为

图12 不同定位孔和加载板厚度工况下谐振板MEFE
(8)
式中:k为低频斜率,dB/oct;N为曲线起始点至拐点频率范围内点的总数目;m为横坐标频率的倍频程数;S(f)为频率f处对应的冲击响应谱值。计算不同定位孔和加载板厚度工况下谐振板MEFE曲线的低频斜率并整理,见表3。从表3中可以看出,低频斜率随着定位孔和加载板厚度的变化而变化,其最小值和最大值分别为12.55 dB/oct和15.44 dB/oct。

表3 不同加载板厚度下谐振板冲击环境拐点值
以上分析表明,综合连接杆的孔位和加载板的厚度两个变量调节因素,冲击环境模拟平台可以实现拐点频率在951 Hz~4 031 Hz内的调节功能,能够基本覆盖航天器中远场火工冲击环境模拟的拐点频率调节需求。
2.6 橡胶减冲器的影响
从冲击环境模拟装置的试验和数值研究结果中可以看出在谐振板上产生的冲击环境在高频部分出现“上翘”现象。分析产生这种现象的原因是由于冲击信号中包含了较多的高频分量所致。工程经验表明,航天器中远场火工冲击环境在高频部分普遍较为平整。因此,“上翘”现象将对航天器中远场火工冲击环境的准确模拟带来一定困难。
在入射杆端部分别粘贴不同厚度的橡胶减震垫片(称为“橡胶减冲器”)进行冲击试验。不同橡胶减冲器厚度工况下谐振板的MEFE,如图13所示。从图13中可以看出,当增设0.75 mm厚度的橡胶垫后,谐振板最高期望飞行环境中高频分量较无橡胶垫工况曲线有了明显下降,高频幅值变得“平整”且“上翘”现象消失。进一步增大橡胶垫的厚度后MEFE曲线的幅值逐渐降低,斜率逐渐减小,拐点频率基本不变。
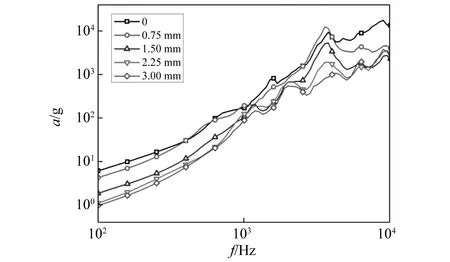
图13 橡胶垫厚度的影响
上述分析表明增设0.75 mm的橡胶垫后能够有效抑制冲击信号中的高频分量,起到“高频整形”的效果。此外,进一步增加橡胶垫的厚度将减弱冲击能量,同时改变谱线的斜率。
2.7 测试设备的影响
在实际工程中待测试的设备并不唯一。不同种类设备之间的结构、尺寸和安装方式等都不尽相同。为了研究待测试设备本身对冲击环境的影响规律,试验中将模拟设备样件去除重新进行标准冲击试验。谐振板上有无设备样件测得的谐振板的MEFE对比,如图14所示。图14中两条曲线整个分析频段内基本接近,两条谱线的拐点频率和低频斜率也基本相同。分析表明设备模拟样件对谐振板的冲击环境影响不大,提出的冲击环境模拟装置的参数影响规律对一定尺寸和质量范围内的待测试设备都具有适用性。

图14 冲击环境模拟装置有无设备样件两种工况的MEFE对比
3 算例验证
3.1 冲击响应谱的标准化
典型火工冲击时域信号如图15所示。将图15中曲线数据进行冲击响应谱换算获得图16中实线所示曲线,其反映了设备所经受的实际冲击环境。由图16可知该冲击响应谱形状并不规则,即冲击谱的三要素并不明显。因此该信号并不能直接用作冲击试验条件,需进一步标准化处理。本文对冲击响应谱的标准化处理方法分为以下三步。首先,在原始冲击响应谱曲线中确定拐点频率如图文字描述所示。然后,将此频率至终止频率所对应的曲线值进行数值平均,同时将该平均值作为标准化后的高频幅值部分,如图中高频部分虚直线所示。最后,计算原始冲击响应谱起点位置至拐点频率处所有点的斜率的平均值,并将该值作为低频斜率。当拐点频率和低频斜率确定后便可确定低频部分的冲击响应谱斜线。计算处理完成的图15火工冲击信号的标准化曲线(或称为“冲击试验条件”)如图16中虚线所示。通过上述步骤可获得任意冲击响应谱曲线的三要素,即得到其标准化形式。

图15 典型火工冲击信号
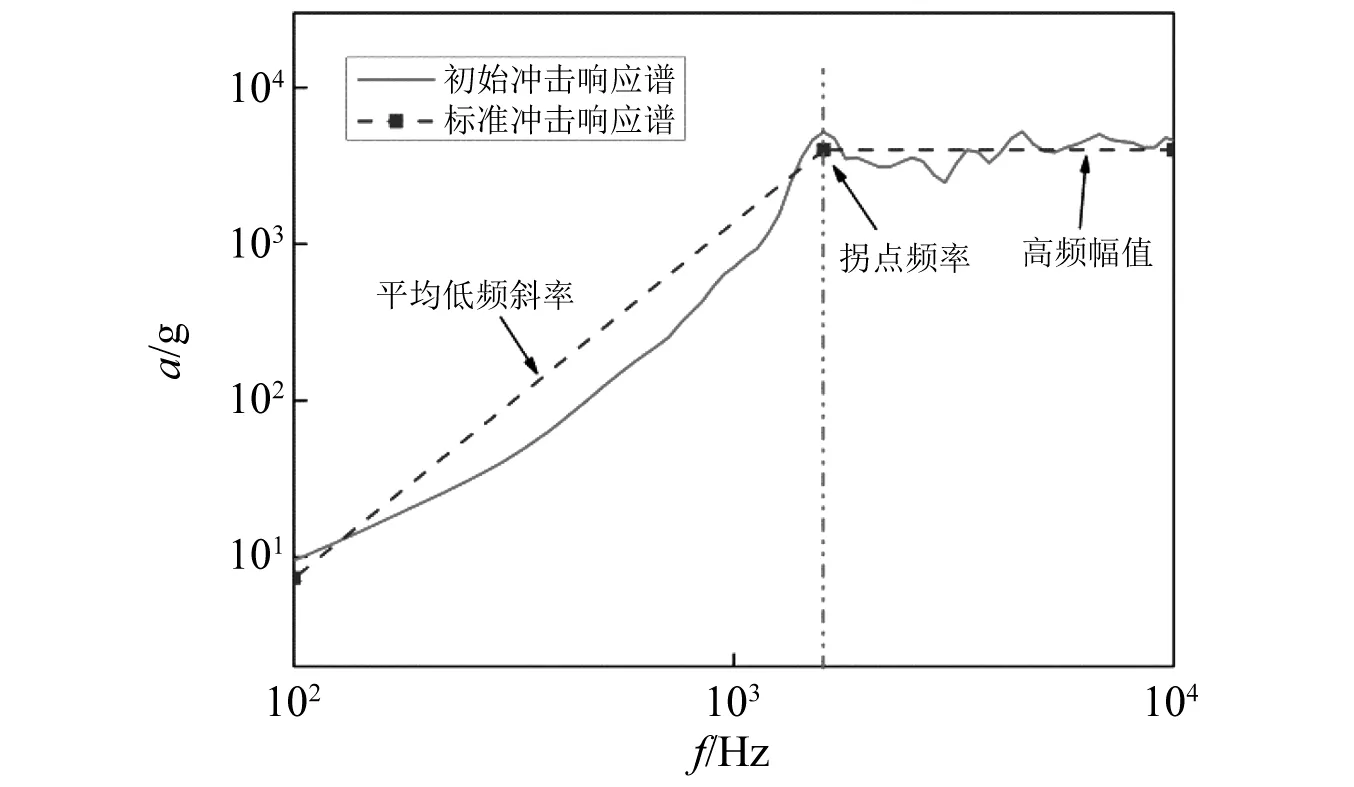
图16 冲击响应谱标准化
3.2 冲击环境模拟及分析
在第2章中给出了冲击环境模拟装置的调节参数对谐振板上冲击环境的影响规律。其中,轻气炮气室压强仅对谐振板上冲击环境的幅值产生影响,表现为独立的影响效应。连接杆的定位孔和加载板厚度变化对谐振板上冲击环境的影响主要表现为拐点频率的调节,同时会对冲击环境的低频斜率和峰值产生耦合影响。因此,利用该冲击环境模拟装置根据冲击试验条件进行试验时,其装置参数调节策略如图17所示。首先,将火工冲击试验信号进行标准化,得到冲击试验条件的冲击响应谱三要素。然后,根据试验条件的拐点频率和低频斜率在表3中查找与之接近的工况,从而确定定位孔和加载板厚度。再后,根据冲击试验条件的高频峰值和定位孔工况结合式(7)计算轻气炮气室的输入压强。试验前在入射杆端部黏接0.75 mm厚度的橡胶垫进行高频整形。最后进行冲击试验并将谐振板上冲击环境与试验条件进行对比分析,必要时须重新调节装置参数并进行试验直至谐振板上冲击环境与试验条件一致为止。

图17 冲击环境模拟装置参数调节策略
在3.1节中典型火工冲击信号标准化后的冲击响应谱三要素信息如下:拐点频率为1 600 Hz,低频斜率平均值为13.67 dB/oct,峰值为3 987.64g。查表3可知,两种工况与试验条件中的拐点频率和低频斜率接近,分别为:定位孔“h3”,加载板厚1.5 cm(f=1 586 Hz,k=13.16 dB/oct);和定位孔“h5”,加载板厚1.7 cm(f=1 510 Hz,k=13.65 dB/oct)。本文选择前一种工况。根据式7(b)定位孔“h3”下高频峰值和轻气炮压强关系计算得到3 987.64g下的输出压强应约为0.07 MPa,考虑到橡胶垫对冲击响应峰值的衰减效应,适当增大轻气炮的压强为0.08 MPa。综上所述,在提出的火工冲击环境模拟装置上实现上述冲击试验条件的参数调节方案为:输出压强0.08 MPa,定位孔“h3”,加载板厚1.5 cm。
将模拟装置按照上述方案设置后进行冲击试验。试验结果中谐振板上的MEFE曲线与冲击试验条件对比,如图18所示。从图18中可以看出,除在高频部分个别频率点由于谱型耦合控制等原因超过范围外,基于上述参数设置谐振板的冲击响应谱基本落在冲击试验条件的±6 dB范围内。表明提出的冲击环境模拟装置的可行性和规律的可靠性,有效避免了冲击环境试验前期的反复调试过程。
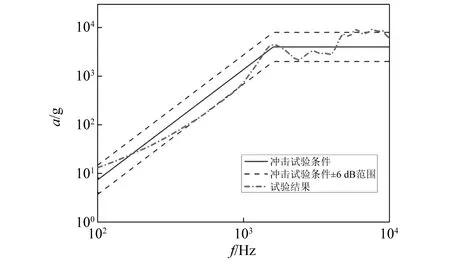
图18 冲击试验条件与冲击环境模拟结果对比
4 结 论
本文提出了一种基于轻气炮加载的多调节参数火工冲击环境模拟装置并总结了谐振板冲击环境谱型控制方法,获得结论如下:
(1)轻气炮气室压强仅对谐振板最高期望飞行环境的幅值具有影响,且幅值的变化规律与轻气炮气室压强近似成幂次方关系。
(2)连接杆定位孔和加载板厚度相结合可以实现谐振板上冲击环境在951 Hz~4 031 Hz内的调节,但同时会对低频斜率产生耦合影响。
(3)在入射杆前端与子弹接触面粘贴一定厚度橡胶垫可对冲击环境起到高频整形效果,但同时会对峰值产生耦合影响。
(4)谐振板上有无样件对冲击环境影响不大,当设备的质量尺寸在与样件相当情况下相关规律仍然有效。
