基于K-Shape 的时间序列模糊分类方法

李海林，贾瑞颖，谭观音,2

（1. 华侨大学信息管理与信息系统系 福建 泉州 362021；2. 华侨大学应用统计与大数据研究中心 福建 厦门 361021）

时间序列是一种与时间相关的数值型数据，基于时间序列的数据挖掘与分析成为目前数据研究领域中最具有挑战性的十大问题之一[1]。分类算法是时间序列数据挖掘中极为重要的任务和技术[2]，有大量关于时间序列分类和挖掘的研究[3]。分类问题依赖于时间序列间的相似性度量，而相似性度量是两条时间序列相似程度的度量方法[4]。对于时间序列来说，同类时间序列间的相似性主要有时域相似性、形状相似性和变化相似性3 种形式[5]。支持向量机（support vector machine, SVM）是由文献[6]提出的通过核函数将时间序列向高维空间映射的方法，可用于时间序列分类。朴素贝叶斯分类器是目前公认的一种简单而有效的概率分类方法，作为经典的机器学习算法之一，在信息检索领域有着极为重要的地位[7]。文献[8]提出了EAIW 分类算法，该算法为时间序列区间赋予权值，采用集成分类的算法，通过权值对时间序列进行分类。文献[9]提出了TLCS 算法，该算法提出一种新的基于时间序列的趋势离散化方法，利用LCS 对其进行相似性度量。

模糊聚类由于能够描述样本类属的中介性，能更客观地反映现实世界，目前已成为聚类分析的主流，成为非监督模式识别的一个重要分支。模糊聚类分析已经成功地应用于遥感图像处理、医学图像处理、基因数据处理、模糊决策分析等领域[10]。众多的模糊聚类方法中，应用最广泛的是模糊C-均值（fuzzy C-means, FCM）算法。由于模糊C-均值算法在初始聚类中心的选择上具有随机性，对初始值比较敏感，难以取得全局最优[11]。

本文提出一种新的时间序列分类方法，即基于k-shape 的时间序列模糊分类方法。该方法利用一种新的k-shape 聚类算法[12]对训练集中每个类的时间序列进行聚类，得到聚类中心群，并将这些中心群作为模糊分类的初始聚类中心，使用模糊C 均值对时间序列测试集数据进行分类。

1 相关理论基础

k-shape 是一种应用在时间序列数据中的聚类方法[12]，此算法提出基于时间序列形态相似性的距离量度方式SBD，并采用一种新的聚类中心计算方式SE 提取每类聚类中心的时间序列曲线形态，以此完成聚类。

定义1 SBD 是一种基于形状的相似性度量方式，在一定程度上弥补了以欧式距离作为相似性评价指标的不足，通过SBD 可得到两条时间序列之间的相似度量。具体过程如下：

(dist,y′)=SBD(x,y)

基于形状的相似性度量方法：

输入：两条Z-score 标准化后的时间序列x，y；

输出：时间序列x，y的相似性度量dist 和y相对于x的对齐序列y′；

计算l en=22*length(x)-1；

对x和y分别进行快速傅里叶变换，即Fx=FFT(x,len)，Fy=FFT(y,len)；

进行逆快速傅里叶变换，计算x和y之间的交相关序列CC，C C=IFFT{Fx*Fy}；

定义 2 SE 是从时间序列中提取最具有代表的形态特征，以此进行聚类。根据文献[12]，k-shape利用SE 方法可以在每种类别的数据中产生一个聚类中心。

基于代表性形态特征的聚类中心提取方法：C=SE(X,R)

输入：Z-score 标准化后的时间序列集合X=[x1,x2,···,xn] （其中每条时间序列的长度为p），与X对齐的参考序列向量R；

输出：聚类中心矩阵C；

设立对齐序列矩阵M；

定义 3k-shape 是一种基于时序形状的时间序列聚类方法。该方法首先利用SBD 算法进行时间序列之间的相似性度量，获得相似序列。然后使用SE 算法从相似序列中提取第一特征向量，作为聚类中心，进而完成聚类。

基于时间序列形态特征的聚类方法：(IDX,C)=k-shape(X,k)

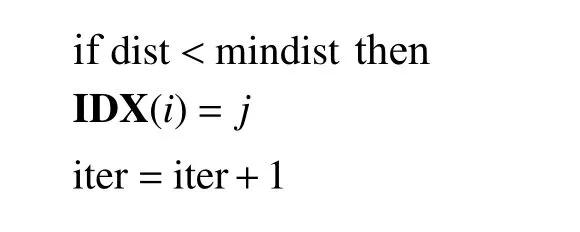
2 时间序列模糊分类

新分类方法首先通过基于k-shape 的聚类中心群方法构建每个类别的聚类中心群，然后结合基于FCM 的模糊分类方法实现对时间序列的分类。该方法具有良好的分类性能。

2.1 基于k-shape 的聚类中心群

绝大多数的时间序列都存在明显的位移和扭曲，传统的聚类算法不能有效解决这部分时间序列的聚类问题，而k-shape 对具有位移和扭曲的时间序列聚类有更好的适用性，可以在一定程度上弥补传统聚类算法以欧氏距离作为相似性度量指标的不足。本文提出一种新的基于k-shape 的聚类中心群方法KCG，该方法可得到单个类别的聚类中心群，且有较好的代表性。

如图1 所示，通过对时间序列数据集X提取聚类中心，可以看出k-shape 提取的聚类中心相比于传统聚类算法k-means 更符合数据集X的形态特征，更具有代表性。其算法过程如下。

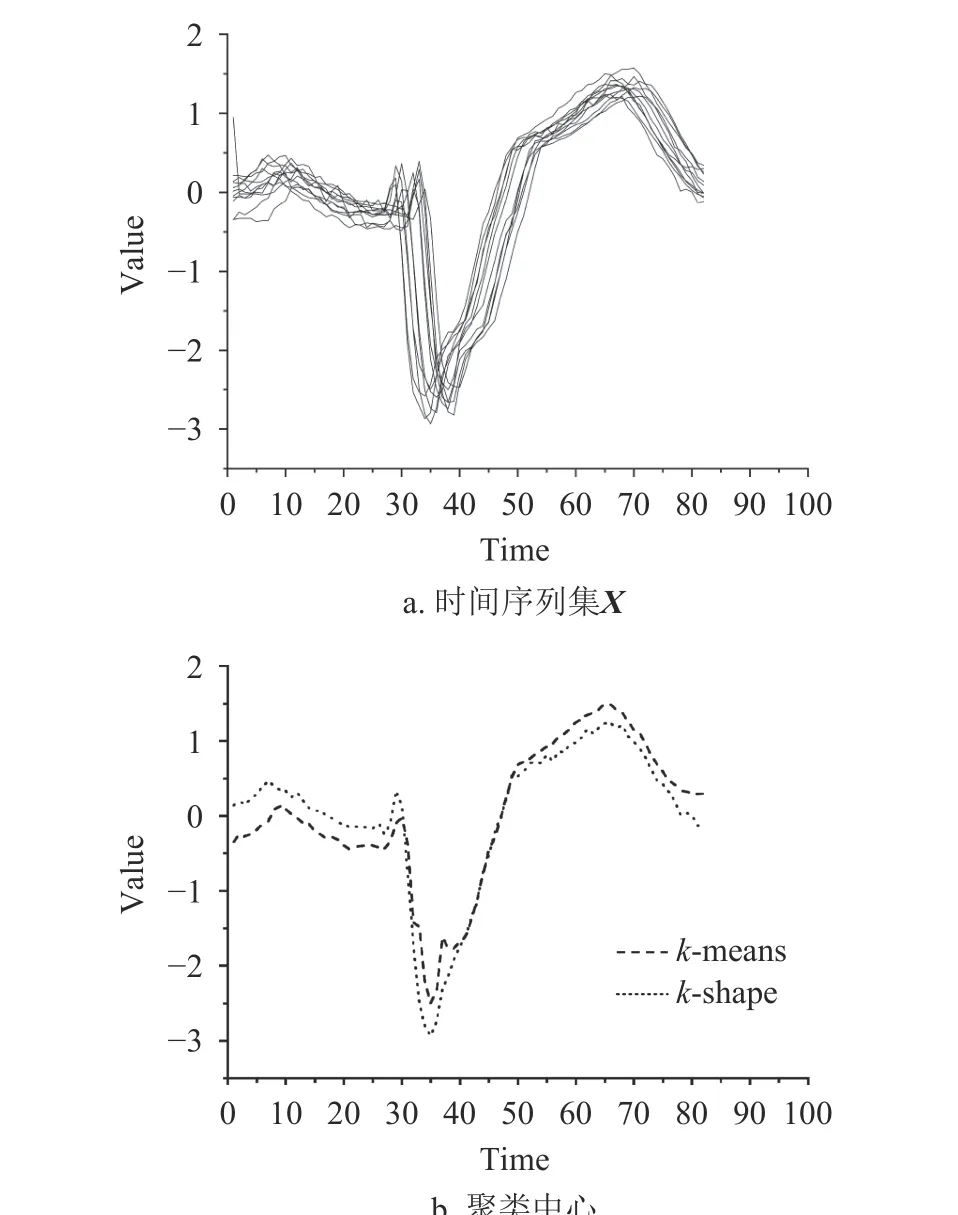
图1 k-shape 算法优势

基于k-shape 聚类的聚类中心群方法：Ca=KCG(X,k)

输入：同一类别的时间序列数据集X=[x1,x2,···,xn]、X的类别标签A和聚类中心数k；

输出：聚类中心矩阵Ca=[c1a,c2a,···,cka]，cia表示A类别的聚类中心群中的第i个中心代表对象；

1） 根据k-shape 聚类算法，将时间序列数据集X划分成k类，得到k个聚类中心，即 (IDXa,Ca) =k-shape(X,k)， IDXa和Ca分别代表X中所有序列的聚类标签向量和聚类中心矩阵；

2） 将步骤1）中得到的聚类中心矩阵Ca标记为Ca=[c1a,c2a,···,cka]， 代表A类别成员序列的聚类中心群。

通过基于k-shape 聚类的聚类中心群方法KCG可以得到同类别时间序列集的聚类中心群，该中心群可代表整个类别的时间序列数据形态特征分布情况。

2.2 模糊分类

模糊分类相比于传统分类算法的硬划分，更符合时间序列分类的不确定性。FCM 算法作为模糊分类的主流算法之一，能在一定程度上解决时间序列数据分类的不确定性问题，是传统硬聚类算法的一种改进。

FCM 算法的核心思想是通过极小化目标函数求最优聚类中心[13]，聚类结果是每一条时间序列对聚类中心的隶属程度，该隶属程度用一个数值来表示。本文提出一种基于FCM 的模糊分类方法，通过已知的初始聚类中心群，进行模糊分类，降低初始值对最后分类结果的影响。为了便于理解和讨论模糊分类方法，假设时间序列数据集共分为两类，进一步解释该算法。其具体算法过程如下：

基于FCM 的模糊分类算法：D= FCM(Y,C,iter_max)

输入：包含已知类别A和 类别B的聚类中心矩阵C、允许的最大迭代次数 iter_max（默认为100）和时间序列测试数据集Y=[y1,y2,···,ym]；

输出：隶属度矩阵D；

1） 将聚类中心矩阵C中A类别的聚类中心群标记为Ca，B类 别的聚类中心群标记为Cb；

2） 根据FCM 模糊聚类算法，将C作为初始聚类中心进行聚类，得到模糊隶属度矩阵D， 即D=FCM(Y,C,iter_max)。

通过基于模糊分类的FCM 算法得到模糊隶属度矩阵D后，进一步分别计算yi属 于D中A类别聚类中心群Ca和B类 别聚类中心群Cb的隶属度之和，并判断大小。较大的隶属度之和代表的类标签为yi所属类别，即可完成分类。

基于FCM 的模糊分类算法以k-shape 聚类得到的聚类中心群作为初始聚类中心，经过一定次数的迭代，得到模糊隶属度矩阵，依次判断测试时间序列属于各类别标签的聚类中心群的隶属度之和，根据最大隶属度原则确定该测试时间序列属于哪个类别，从而完成时序数据的分类。

2.3 基于k-shape 的时间序列模糊分类方法

考虑到k-shape 聚类算法和模糊分类算法的优势，本文将基于k-shape 的聚类中心群算法KCG和基于FCM 的模糊分类算法结合起来，提出了一种思路更为简单的时间序列分类方法（k-shape and FCM based time series clustering, KFCM）。KFCM算法首先将时间序列训练集各类别的序列成员进行k-shape 聚类，分别得到每个类别的聚类中心群，形成已知类标签的聚类中心群。然后，使用基于FCM 的模糊分类算法，将测试集序列与已知标签的聚类中心群进行聚类，输出模糊隶属度矩阵。最后，根据隶属度大小原则进一步判断测试集类别。具体算法如下：

基于k-shape 的时间序列模糊分类方法：L=KFCM(X,Y,k,iter_max)。

输入：训练集X、测试集Y、默认最大迭代次数iter_max 和聚类中心数k；

输出：测试集Y的类标签向量L；

1）根据训练集X=[x1,x2,···,xn]的成员类标签[h1,h2,···,hw]， 依次利用KCG 对类别hi包含的每个成员进行聚类，得到hi的 聚类中心群Ci。将w个聚类中心群合并得到总聚类中心群C，C包含w个类别，共kw个聚类中心；

2）对测试集Y=[y1,y2,···,ym]，使用基于FCM的模糊分类算法，即D=FCM(Y,C,iter_max)；

3）根据步骤2）得到的模糊隶属度矩阵D，计算测试集对象yj属 于D中各类聚类中心群的隶属度之和，其较大者的类标签为yj所 属类别lj；

4）重复步骤3），获得Y中所有成员的类标签，即L=[l1,l2,···,lm]，其中m为测试集Y包含的时间序列数目。

3 数值实验与结果分析

为了验证本文提出算法的有效性，在30 个时间序列数据集上做分类实验。通过实验结果可以验证分类精度的有效性，也可以验证针对存在位移和扭曲特征的时间序列分类，新方法的适用性。

3.1 实验设置

算法代码使用Python 3.7 在Anaconda 科学计算环境中实现，运行所用计算机的CPU 型号为InterCore i5-8250U （1.60 GHz），RAM 为16 GB，操作系统是Windows10 64 位（DirectX 12）。

本文采用的数据集是UCR TS Archive 2015，UCR[14]是时间序列数据集，每个数据集样本都带有样本类别标签，它是目前时间序列挖掘领域重要的开源数据集资源。从UCR 数据集中选取了30 个训练集，为了验证新方法具有更高的分类质量和性能，这30 个数据集在类别、长度和大小上具有明显差异。具体数据集信息如表1 所示。

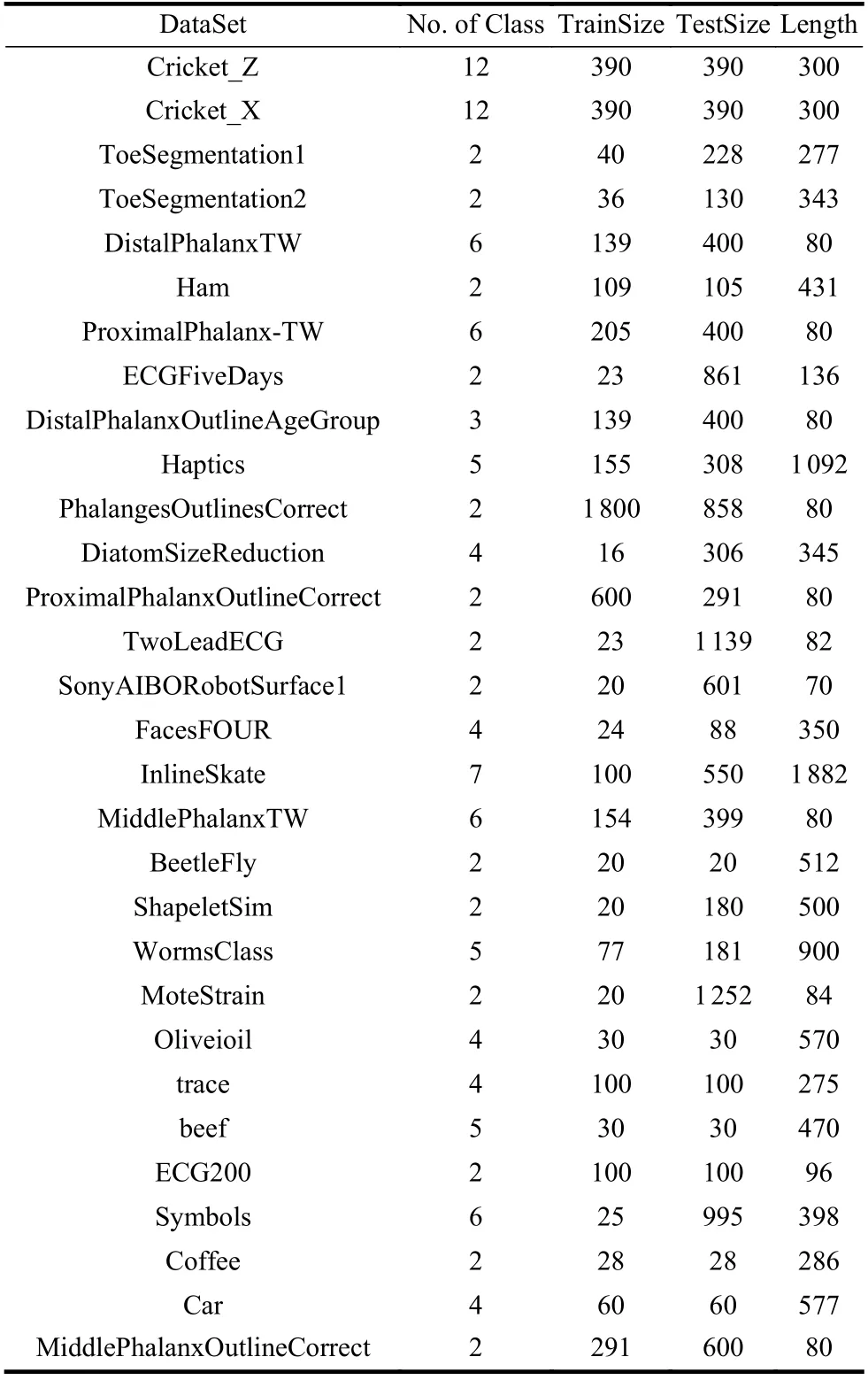
表1 时间序列数据集

在对训练数据集进行k-shape 聚类时，训练集的类别和类别数是已知的，需要用k-shape 单独对训练集每一个类别包含的时间序列进行聚类，进而确定各类别的聚类中心群。

3.2 参数设置

在进行参数讨论时，假定训练集共有w个类别，每个类别的聚类中心数都是k，因此共可得到wk个聚类中心，且每个聚类中心群都标记着本类别的标签。本文以Cricket_X 数据集为例，说明利用手肘法选取最佳聚类数k的过程。k的取值为1～8 （本文设置上限为8）。如图2 所示，随着k增大，SSE 的下降幅度会骤减，在k=4 之后下降幅度趋于平缓。因此针对Cricket_X 数据集，最佳聚类中心数是4。

图2 k值选取对SSE 的影响

3.3 数据分类

本节将提出的KFCM 算法与SVM[6]、Bayes[7]、EAIW[8]和TLCS[9]这4 种基准分类算法进行比较。为了进一步验证k-shape 在提取聚类中心过程中的算法优势，本文利用k-means 算法提取各类别的聚类中心群来作为模糊分类的初始聚类中心，同时使用模糊分类方法对时间序列数据集进行分类。该算法称为KMFCM，作为KFCM 的对比算法之一。利用以上6 种方法对30 组UCR 数据集进行分类实验，分类错误率如表2 所示。利用平均分类错误率、方差和胜出率3 个指标评价分类效果，如表3所示。

从表2 可知，KFCM 算法的平均错误率最低，错误率的总体波动幅度较小，在30 个数据集中有9 个数据集的错误率最小，有最高的胜出率。为了更好地表现分类结果，本文通过对错误率的两两比较，使用可视化分类比较结果展示，如图3 所示。KFCM 的分类准确率和胜出率都高于KMFCM，同时，在ShapeletSim、MoteStrain、InlineSkate 等数据集上也有较低的分类错误率，这证明了k-shape相比于k-means 在聚类过程中有明显优势。KFCM在时间序列测试集上的分类性能优于SVM 和Bayes，平均准确率有一定提升。最后，KFCM 分类准确率相较于TLCS 和EAIW 也有一定提高，个别数据集提高效果较为明显。

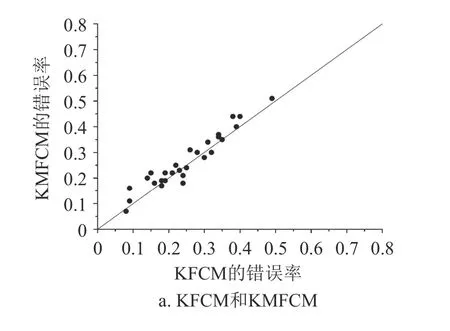
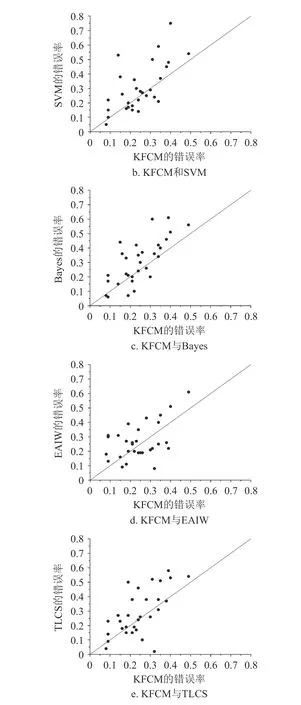
图3 分类算法错误率的比较

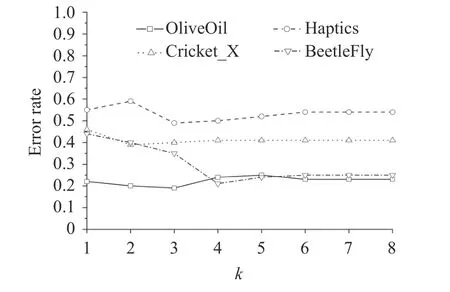
图4 k与错误率的关系

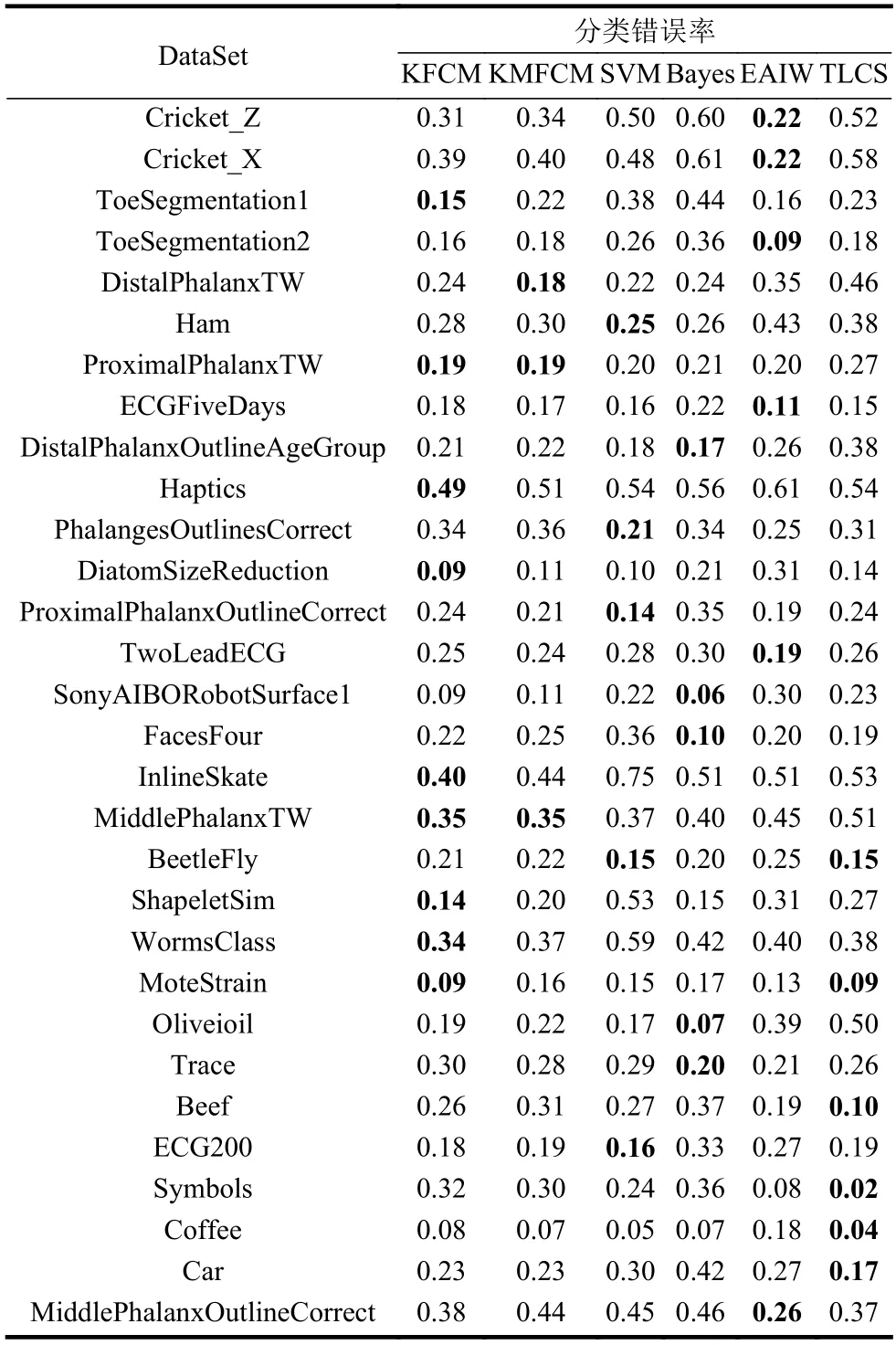
表2 各分类算法分类错误率

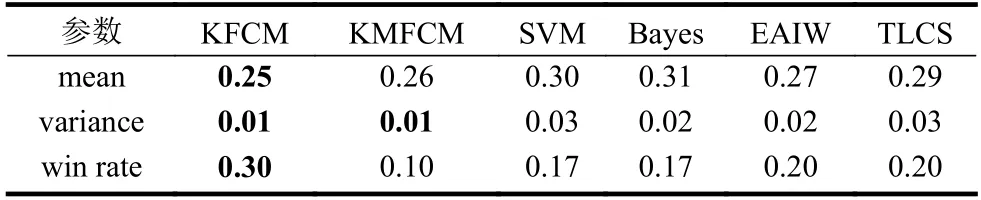
表3 各类算法评价指标

本文选取4 个时间序列数据集，来说明聚类中心数k对分类结果的影响，如图4 所示。k值对各数据集的分类结果影响不同，对于BeetleFly 数据集，错误率最大值和最小值之间差距达到0.23；对于OliveOil 数据集，错误率最大值和最小值之间差距为0.06。

由此可知，对于不同的数据集，k对最后分类效果的影响也是不同的。有的数据集如BeetleFly受影响比较大，因此参数k需根据具体数据而设定。

3.4 实验分析

本文分析了30 个时间序列训练集中部分时间序列数据的特点，将时间序列训练集按照是否存在明显位移和扭曲的特点分为两大类，计算每一类的平均错误率。横向比较，新方法KFCM 在存在明显位移和扭曲特点的时间序列平均错误率要比趋势较为一致的时间序列平均错误率要低；纵向比较，对于存在明显扭曲和位移的时间序列集，新方法KFCM 相比其他5 个方法的错误率低，分类性能更好。

从 图5 中 看 出，InlineSkate、MoteStrain 和ShapeletSim 这3 个时间序列数据集具有较明显的位移和扭曲，故SVM、Bayes 和KMFCM 在处理此类的数据集分类时存在较大的不足，但KFCM算法表现良好。Symbols、TwoLeadECG 和Car 这3 个时间序列集中同一类时间序列数据上“几乎”不存在位移或者扭曲，故SVM、Bayes 和KMFCM 在这3 个数据集上的分类效果比较理想。图6 也表明新方法KFCM 在InlineSkate、MoteStrain 和ShapeletSim时间序列数据集上有更低的错误率。

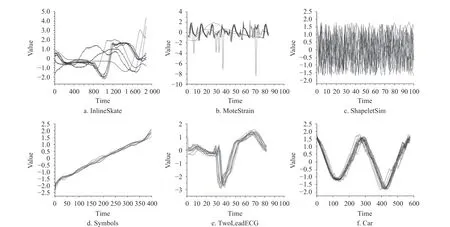
图5 部分训练集中label=1 的时序数据

图6 部分数据集错误率比较

3.5 时间效率比较

时间序列分类的性能不仅体现在分类效果上，而且也包含了算法的整体时间消耗。为了更直观的比较以上6 种分类方法的时间效率，本文随机抽取了 WormsTwoClass、 Ham、 Beef 和 FaceFour 这4 个时间序列数据集，进行方法运行时间效率的对比实验。

由图7 可知，KFCM 方法在4 个时间序列数据集上的时间效率比KMFCM、SVM 和Bayes 低，分类时间较长。但相比于EAIW 和TLCS，KFCM方法所花费的时间则相对较少。总体来讲，KFCM的时间效率要高于EAIW 和TLCS，低于SVM、Bayes 和KMFCM。文献[15]在大型电力负荷时间序列曲线聚类实验中证明k-shape 的时间复杂度高于k-means。本文研究的时间序列分类方法主要是通过k-shape 提取聚类中心群，该阶段的计算复杂度较高，导致整体算法在大数据环境下的时间效率较低，并不适用于大型数据集。但结合分类质量来看，KFCM 可以使用较高的时间效率来获得较好的分类效果。

图7 部分数据集时间效率比较

4 结 束 语

鉴于k-shape 在时间序列数据聚类领域的优越性，本文提出了一种新的时间序列分类方法KFCM。该方法首先利用k-shape 对时间序列数据训练集中的各个类别包含的成员进行聚类，得到聚类中心群。然后，将聚类中心群作为模糊分类的初始聚类中心，根据隶属度最大原则确定测试时间序列数据的类别标签。通过实验验证，与传统时间序列分类方法相比，新分类方法具有以下优势：1）通过使用k-shape 聚类算法，提高了对具有位移和扭曲特征的时间序列数据集分类的适用性，在一定程度上弥补了传统聚类算法以欧氏距离作为相似性指标的不足；2）新分类方法可以利用手肘法确定最佳聚类数，减小参数变化对最终分类结果的影响；3）与传统分类方法相比，新分类方法能够实现更好的分类效果，具有一定的优越性。然而，该方法相较于传统分类方法SVM 和Bayes 有较高的时间复杂度，在大型数据集上应用效果不佳，这是未来需要进一步研究的工作。