关于粒度重要性公式的改进

卢加学， 汪小燕

（安徽工业大学 计算机科学与技术学院，安徽 马鞍山 243032）

1982 年波兰Pawlak 教授首次提出粗糙集理论[1]，粗糙集理论在处理不确定性、不精确性以及不完全数据方面有着巨大优势，主要的研究内容是属性约简[2]和规则提取。 粗糙集理论中的属性重要度体现的是去掉某个或某些属性前后知识库分类变化的程度。对此，许多学者进行了研究。文献[3-4]给出了基于代数观的由属性依赖度确定属性重要度的方法。 但属性依赖度度量在某些情况下处理数据存在局限性，从而得不到合理的结果。文献[5]提出了包含度理论。文献[6]结合信息熵的特点，给出了基于信息观的条件信息熵的属性重要度方法。 文献[7]对经典依赖公式研究，引进多数包含关系，提出了新的知识依赖性度量方法。 属性重要度的确定方法可以为属性约简以及属性权重问题的研究提供基础。

然而以上的文献方法皆是基于单粒度来确定属性重要度，但在实际应用中多粒度往往起着更重要的作用。多粒度粗糙集[8-9]是一种新型的多视角数据分析方法，众多学者对其进行了研究。粒度重要性的确定方法也为多粒度粗糙集中属性约简以及属性权重问题的研究提供了基础。 孟慧丽等人在文献[10]中将信息量引入悲观多粒度粗糙集的下近似分布约简，定义了粒度的重要度，以粒度的重要度作为启发信息设计了约简算法。 但基于等价关系的悲观多粒度的下近似分类条件过于严格，在实际问题中忽略了一定的误差允许。文献[11]将变精度概念引入多粒度，根据近似质量定义变精度的粒度重要度，以此设计了约简算法，但有时也没法判断粒度之间的区别。 文献[12]基于近似质量定义了内外部粒度重要度并结合三支决策模型可以有效的进行粒度的约简。 文献[13]从代数角度定义了变精度多粒度粗糙集，但并未对粒度重要性进行研究。

笔者基于文献[7]，结合多粒度粗糙集理论，提出一种新的粒度重要性度量方法，为进一步区分不同粒度的重要性，加入可信系数计算粒度的重要性，使得分析结果更加合理。 最后，通过一个决策信息系统验证此方法，结果表明该方法是有效的。

1 粗糙集的相关理论

定义1[1]设四元组S=（U，C∪D，V，f）称为信息系统，其中U 表示对象的非空有限集合，称为论域；AT表示属性的非空有限集合；Va表示属性a 的值域，V 表示全部对象在各个属性上的取值构成的集合；f 表示U×AT→V 的一个信息函数，∀a∈AT，x∈U，f（x，a）∈Va。

定义2[1]设S=（U，C∪D，V，f）为信息系统，∀A⊆AT，定义属性集A 的不可区分关系IND（A）为：IND（A）={（x，y）∈U×U|∀a∈A，f（x，a）=f（y，a）}，U/IND（A）表示不可区分关系IND（A）在U 上导出的划分，简记为U/A。 对∀x∈U，[x]A={y|f（y，a）=f（x，a），∀a∈A}称为x 在属性集A 下的等价类。

定义3[1]设S=（U，C∪D，V，f）为信息系统，∀A⊆AT，X⊆U，X 关于属性集A 的下近似集和上近似集分别定义为：A（X）={x∈U:[x]A⊆X}，A（X）={x∈U:[x]A∩X≠Ø}。

定义4[7]设S=（U，C∪D，V，f）为信息系统，∀A⊆AT，X⊆U，X 关于属性集A 的依赖度定义为

这里POSA（X）表示X 的A 正域，也就是X 关于属性集A 的下近似集，|·|表示集合的基数。

定义5[7]设S=（U，C∪D，V，f）为信息系统，Ø⊂P⊆C，Ø⊂Q⊆D 给定ρ∈P 依据依赖度的定义，给出属性重要度公式

如果sig（ρ，P，Q）=0，则称ρ 在P 中关于Q 是不重要的；否则ρ 在P 中关于Q 是重要的。

2 多粒度粗糙集相关理论

定义6[10]在多粒度粗糙集中，四元组S=（U，C∪D，V，f）是一个完备信息系统，其中A1，A2，A3，…，Am⊆AT。 每个属性集称为一个粒度，对U 基于等价关系IND（Ai）划分得到一个粒度空间，A={A1，A2，A3，…，Am}称为一个粒度集。 ∀X⊆U，X 的悲观多粒度下近似、上近似分别定义为

定义7[12]四元组S=（U，C∪D，V，f）是一个完备信息系统，A={A1，A2，A3，…，Am}，决策属性D 导出的划分为U/D={X1，X2，X3，…，Xs}。 近似质量的定义如下

其中，△∈{P，0}表示悲观和乐观多粒度粗糙集两种情况。

定义8[10]四元组S=（U，C∪D，V，f）是一个完备信息系统，A={A1，A2，A3，…，Am}，决策属性D 导出的划分为U/D={Y1，Y2，Y3，…，Yn}，定义悲观多粒度下粒度集A 的信息量如下

定义9[14]四元组S=（U，C∪D，V，f）是一个完备信息系统，A={A1，A2，A3，…，Am}，决策属性D 导出的划分为U/D={Y1，Y2，Y3，…，Yn}，β∈（0，1]，定义变精度悲观多粒度下粒度集A 的β 下近似分布粒度熵如下

3 新的近似质量及粒度重要性的改进

3.1 近似质量的改进

定义7 中的近似质量是依据悲观和乐观下近似计算的，但基于等价关系的分类是精确的，忽略了实际应用中集合一定程度上的包含关系，这就会导致出现近似质量相同的情况以至于无法区分两个粒度的重要性。为解决该问题，文中提出基于近似质量公式、以多数包含关系为前提新的知识依赖性度量公式，使得结果的分析更加可靠。

例如文献[15]中的实例分析，见表1。

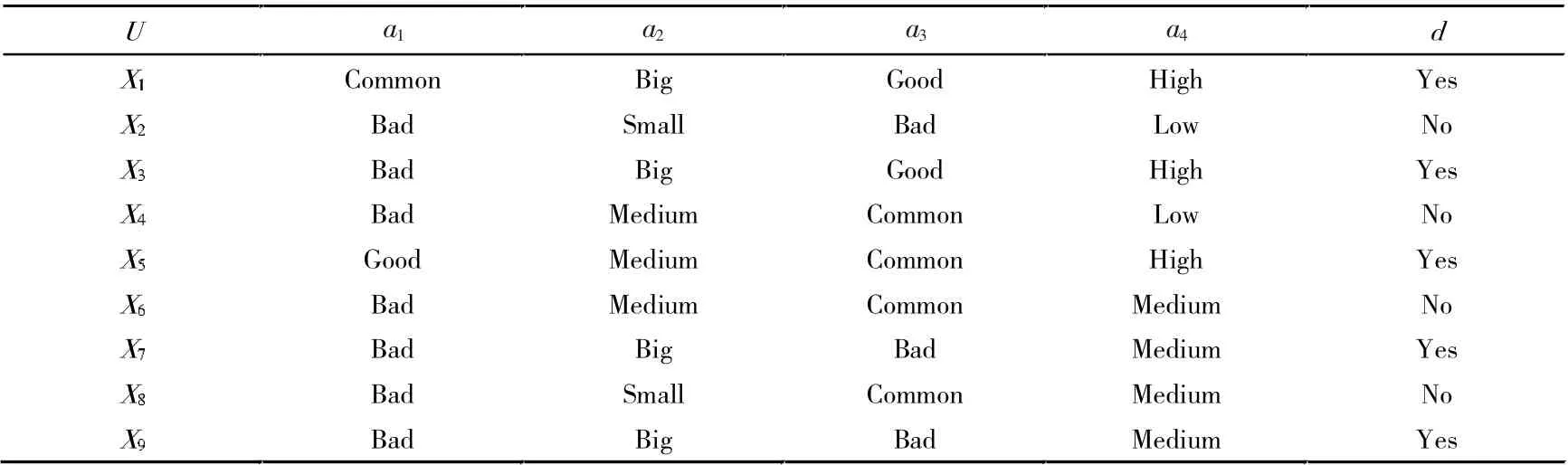
表1 风险投资决策信息系统表

其中条件属性子集族A={A1，A2，A3，A4}={{a1}，{a2}，{a3}，{a4}}，U/D={D1，D2}={{x1，x3，x5，x7，x9}，{x2，x4，x6，x8}}。 依据近似质量公式中的悲观下近似计算各个粒度的依赖度，发现粒度A1和A3对于决策分类D2出现A1（D2）与A3（D2）为空集的情况，使得多个粒度的重要性为0 ，无法直观的判断粒度之间的重要性。 出现这种问题的原因是近似质量公式有一定的局限性。 为解决此问题，在近似质量公式上引入多数包含度的概念。

定义10[5]（多数包含度）设U 是有限非空集合，P（U）表示U 的所有子集构成的幂集，对于∀A，B∈P（U），记

则称D0（B/A）为A 关于B 的多数包含度，即B 包含A 的程度。

定义11[7]（相对错误分类率） 设X 和Y 表示有限论域U 的非空子集。 相对错误分类率有如下定义

其中D0（Y/X）=|X∩Y|/|X|。

定义12[7]（多数包含关系） 令0≤β<0.5，若

成立，则X 与Y 满足多数包含关系。

依据以上的概念定义新的近似质量公式。

定义13 四元组S=（U，C∪D，V，f）是一个完备信息系统，A={A1，A2，A3，…，Am}为粒度集合，决策属性D导出的划分为U/D={Y1，Y2，Y3，…，Yn}。 如果Ai与D 满足多数包含关系，则其定义为

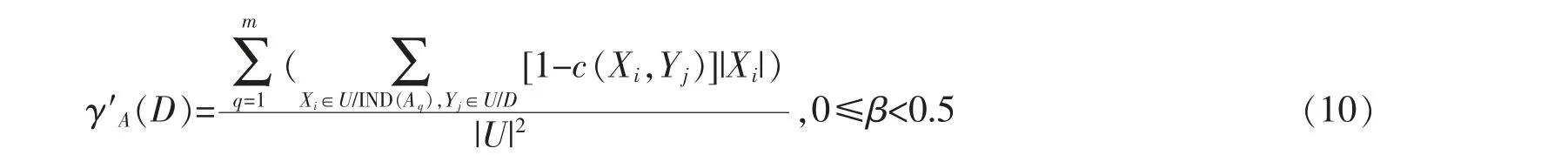
定理1 令四元组S 是一个完备信息系统，A={A1，A2，A3，…，Am}为粒度集合，决策属性D 导出的划分为U/D={Y1，Y2，Y3，…，Yn}。 0≤β<0.5，B⊆A，则有γ′B（D）≤γ′A（D）。

证明 因为B⊆A，对于B={A1，A2，…，An}，n≤m，因此

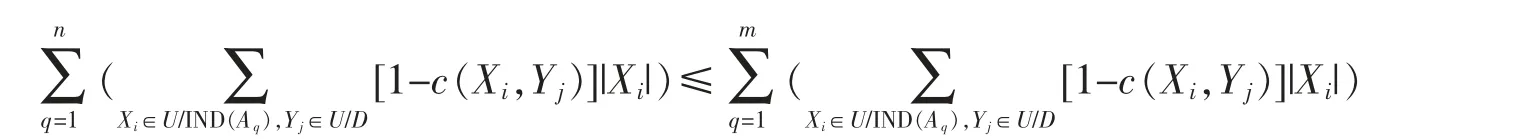
故有γ′B（D）≤γ′A（D）。

定理1 说明随着多粒度集中的粒度的增加，近似质量也随着增大。

定理2 令四元组S 是一个完备信息系统，A={A1，A2，A3，…，Am}为粒度集合，决策属性D 导出的划分为U/D＝{Y1，Y2，Y3，…，Yn}，且0≤β1≤β2<0.5，则有

证明 定义13 公式中的[1-c（Xi，Yj）]|Xi|可约简成|Xi∩Yj|，表示的是在参数β 的条件下两集合相交的程度，当0≤β1≤β2<0.5，如果有c（Xi，Yj）≤β1，则有c（Xi，Yj）≤β2，此时Xi⊆β1Yj，则一定有Xi⊆β2Yj，按照定义13 的

公式则结论成立。

定理2 说明了在多粒度的框架下，随着阈值β 的单调变化，粒度的依赖度也随之单调变化。

定理3 令四元组S=（U，C∪D，V，f）是一个完备信息系统，A={A1，A2，A3，…，Am}为粒度集合，决策属性D导出的划分为U/D＝{Y1，Y2，Y3，…，Yn}，当β=0 时，则有

定义14 四元组S=（U，C∪D，V，f）是一个完备信息系统，Ai∈A={A1，A2，A3，…，Am}，属性D 导出的划分为U/D＝{Y1，Y2，Y3，…，Yn}，在粒度集A 上，Ai关于D 的粒度重要性定义如下i

推论1 四元组S=（U，C∪D，V，f）是一个完备信息系统，A={A1，A2，A3，…，Am}为粒度集合，决策属性D导出的划分为U/D＝{Y1，Y2，Y3，…，Yn}，当γ′A（D）=γ′A-{Ai}（D）时，表明粒度Ai在粒度集A 中关于D 是不重要的。

定义15 四元组S=（U，C∪D，V，f）是一个完备信息系统，A′⊆A={A1，A2，A3，…，Am}，∀Ai∈A-A′，定义Ai关于D 的粒度重要性如下

最后，通过定义14 来计算表1 中的sig′（A1，A，D）=2/81，sig′（A2，A，D）=7/81（即β=0.4 时，A1，A3对D 的依赖度分别是2/81，7/81）。 根据定义14 计算的结果可以区分两个粒度的依赖度，更符合实际应用。

3.2 粒度重要性公式的改进

为进一步区分不同粒度的重要性，加入可信系数计算粒度的重要性，使得粒度重要性计算结果更加合理。

定义16 （可信系数） 四元组S=（U，C∪D，V，f）是一个完备信息系统，A={A1，A2，A3，…，Am}为粒度集合，设A 中去掉一个属性集Ai的一个子集P=A-{Ai}，那么P 关于U/A 的可信系数有如下定义

定理4 可信系数有如下性质

证明 由定义16 显然易证0＜τ{A-Ai}＜1。

定义17 四元组S=（U，C∪D，V，f）是一个完备信息系统，Ai∈A={A1，A2，A3，…，Am}，属性D 导出的划分为U/D＝{Y1，Y2，Y3，…，Yn}，Ai关于D 的粒度重要性定义如下

下面通过实例分析验证定义的可行性。

4 实例分析

表2 是一个学生面试的决策信息表，其中U={X1，X2，X3，X4，X5，X6，X7，X8，X9}为论域，表示参加面试的学生。条件属性集C={a1，a2，a3，a4}表示不同学科的老师给出的专业评价，决策属性d 表示学生面试是否通过，信息表见表2。

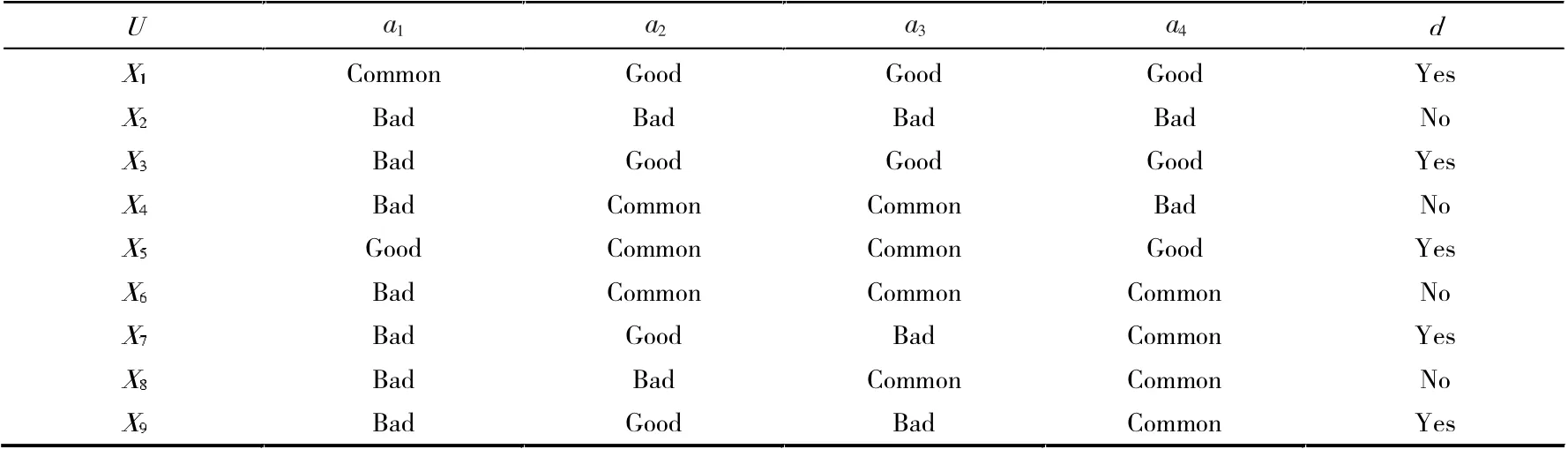
表2 决策信息表

令条件属性集A={A1，A2，A3，A4}={{a1}，{a2}，{a3}，{a4}}。 有如下划分

A-{A1}，A-{A2}，A-{A3}，A-{A4}关于U/A 的可信系数分别为3/4，3/4，3/4，3/4。

下面通过几种确立粒度重要性的方法，结合上述分类信息进行重要性的刻画，得到结果见表3。

表3 各属性重要性的对比

表3 中M 表示方法，方法1、2、3 分别对应基于信息量的悲观下近似度量（定义8）、基于下近似分布粒度熵的多粒度变精度度量（定义9）、文中提出的定义17。 在β，k的取值范围选择两组参数，方法3 中β 的参数选取则是与方法2 中的参数k 是分别对应的，当k+β=1 时，两种方法中的集合多数包含关系是一样的，这样求解的结果更具有对比性。 由表3 可见，依据方法1 求解时，只有粒度A1不为0，当粒度重要度为0 时没法区分各个粒度之间的重要性而且对粒度权重的计算有影响。 方法2 随着参数k 取值的不同会影响到粒度重要性的变化，可以看出粒度集的重要性变化不大，有时也没法区分粒度之间的重要性。

根据文中所提出的方法，可以直观的表现出每个粒度的重要性的差别，为计算粒度的权重提供了依据。

5 结语

在近似依赖质量的基础上，引入多数包含度的概念，允许集合有一定程度的包含关系，并加入可信系数提出新的粒度重要性公式，并将它应用在学生面试决策系统中说明它的可行性。 接下来的工作是将粒度重要性公式应用到教学数据中，指导相关的教学工作和决策。