基于CPT 的振动沉桩贯入分析理论模型

李卫超，庞玉麟，金易，杨敏

（1.同济大学 土木工程学院，上海 200092；2.上海公路桥梁（集团）有限公司，上海 200433）

近年来由于经济快速发展，城市交通的压力越来越大.作为既有道路改造项目的主要选择，预制拼装高架桥已成为缓解市政交通压力的一种主要形式，如上海市多条道路改造均采用此方案.采用预制拼装的方式建造高架桥具有如下特点：①目前除连接桩基与墩柱的承台为现场浇筑外，其他构件均为工厂预制+现场拼装；②施工快捷、绿色，极大地降低了道路改造期间对交通、周边环境等的不利影响.由于桩基础能够较好地保证承载力、控制构筑物的沉降和不均匀沉降[1]，因此钢管桩成了预制拼装高架桥的首选基础形式.对于钢管桩基础，其常见的沉桩方式有静压沉桩、打入沉桩和振动沉桩[2]，其中静压桩具有无噪音、无振动和无冲击力的特点，但设备笨重、转移困难；锤击沉桩有构造简单、使用广泛的优点，却存在噪音大、废气污染、冲击力大、易损坏桩身等问题；振动沉桩工法具有施工效率高、设备转移方便等特点.因此，振动沉桩工艺成为了当前既有道路改造工程中的首选施工工艺.振动沉桩的原理是通过桩锤内部偏心构件旋转，沿桩基长轴方向产生大小周期性变化的激振力，带动桩基沿轴线方向小振幅振动、降低桩周土阻力，从而驱动桩的沉入[3].然而，在当前实际工程施工中，有部分桩基未能按原设计方案沉至设计标高，不得不根据现场情况调整施工参数.针对部分沉桩困难的桩基，按目前施工经验，要求在一定激振力下连续振沉一定时间，确认不能沉至设计标高后，方可采取截桩措施.需要说明的是，在连续强振过程中，将不可避免地增加桩身结构疲劳损伤.可见，这些问题将不可避免地对工程进度与结构安全度等产生不利影响.

为了分析贯入过程中桩基的可贯入性、桩身应力大小及疲劳损伤等问题，针对振动沉桩贯入过程的预测，分别基于桩身为刚体或弹性体的假设，有学者开展了对应的理论研究.将桩作为刚体的理论解答又可分为解析解和数值解两类，其中解析解一般将地基简化为单层土，桩身视为刚体，定性分析土体和桩锤参数对沉桩过程的影响及沉桩时能量的耗散情况等[4-6]；数值解法可采用较为复杂的桩土作用模型，如在桩周土作用力仅与桩土相对速度有关的假设下，Holeyman 等[7-9]提出并发展的HYPERVIB 模型；Vanden[10]提出的考虑土体间剪切的Vipere 模型；Wong 等[11-12]和Lee 等[13]基于Ramberg-Osgood 本构关系的桩土界面相互作用模型等.针对这些数值模型预测结果的可靠性，Viking[14]、Whenham[15]等学者指出HYPERVIB 模型[7-9]计算时，需要贯入各深度时的初始速度，而这一参数估算困难；Vipere 模型[10]在贯入深度较小时预测贯入速度与实测值存在较大差异；Wong 和Lee 等[11-13]提出的模型需要输入的参数较多、且参数值鲜有与土体的物理力学性质指标、原位测试结果建立明确联系，因此目前应用非常有限.将桩视为弹性体的模型相对较为复杂，通常采用数值方法求解，其中最为常见的方法有一维波动方程法[16]和有限单元法[17].一维波动方程法最早由Smith[16]提出，并首先被应用于打入沉桩的模拟中，后被应用于振动沉桩的分析[18-19].由于该方法将桩身离散为数个单元，单元间的相互作用通过弹簧模拟、桩单元与桩周土相互作用采用桩土相互作用弹簧模拟，因此可认为采用桩单元-弹簧系统模拟沉桩过程.该方法具有求解原理简单、对计算资源要求相对较低等优点，因此在锤击沉桩理论分析中得到了广泛的应用.

桩基贯入的分析理论主要包含有桩锤传递至桩头的激振力和桩土作用模型，其中桩土作用模型及其参数的确定尤为重要，且影响因素较多，具有较大的不确定性.需要强调的是，预制桩在沉桩过程中，桩周土体会受到不同程度的扰动[20]，如孔隙水压力上升[21-23]，强度明显降低等[4，24-27]，因此，在模拟沉桩过程中桩土相互作用时直接采用当地或规范推荐的、多数基于一定休止期后开展的静载试验得到的土层承载力或摩阻力推荐值的做法，很可能导致对桩基贯入阻力和设备沉桩能力误估等问题.为解决该问题，基于现场原位试验，如静力触探试验（Cone Penetration Test，CPT），估算沉桩时桩土相互作用力的方法受到了关注，并得到了一定的应用.基于CPT 预测桩基贯入过程这一做法主要源于静力触探试验锥尖贯入与沉桩过程具有较强的相似性，因此通过CPT试验实测结果估算桩基贯入过程中桩土作用力具有较强的合理性.当前学者已提出了基于CPT 估算桩基静载条件下承载力的方法[28-30]，且得到了较好的应用[31-33]，如Jardine 等[28]提出的ICP-05 法.但目前仅有部分研究[33]将该方法与锤击沉桩的预测理论结合，鲜有应用于振动沉桩分析的报道.

本文基于一维波动方程和ICP-05 方法，建立了振动沉桩工艺下桩基贯入过程的分析理论模型，编写对应的计算程序；通过实测案例对本文理论模型与程序进行验证，并进一步讨论了桩锤工作频率、偏心力矩和配重对桩基贯入过程中桩身位移、桩身应力等的影响特征，为实际工程中桩基可贯入性分析、桩身疲劳损伤验算奠定基础.

1 理论模型的建立与程序实现

1.1 控制方程

令桩身任意深度处在t 时刻的位移（桩相对土向下移动时为正）为u.若桩为一均匀横截面桩，桩的净截面积为Ap，桩身弹性模量为Ep，则桩身所受轴力（受压为正）P 为：

截取桩身上一长度为dz 的单元（见图1），令桩身单位面积所受土阻力为τ，桩周长为Cp，桩身材料密度为ρp，重力加速度为g，由图1 所示的单元沿轴向受力可知该单元所受合力F（向下为正）为：

图1 单元体受力分析Fig.1 Force on a pile element

将式（1）代入式（2）可得：

式（3）即为一维波动方程的控制方程.

针对式（3）的求解，首先将桩土体系参照图2 形式进行离散，即将桩沿深度方向离散为一系列长度为Δz 的桩单元，桩锤与桩头、桩单元之间通过弹簧连接，桩土作用通过弹簧与阻尼器模拟.其中桩单元之间的相互作用通过弹簧模拟；桩土作用弹簧代表了桩周土对桩基的静阻力，阻尼器则是桩周土对桩基的动阻力模拟.

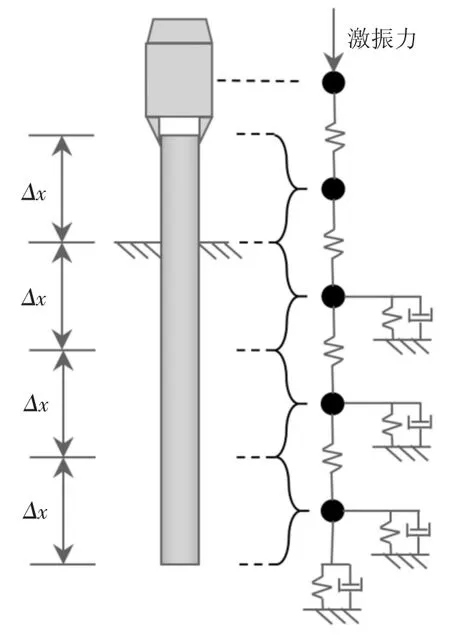
图2 桩-锤-土离散示意图Fig.2 Illustration of discreted pile-hammer-soil

本文采用有限差分法求解，令分析时间步长为Δt，位移对深度采用中心差分、对时间采用向前差分，见式（4）.

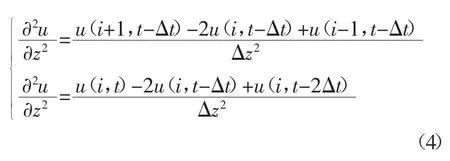
因此，控制方程（3）可表达为式（5）.

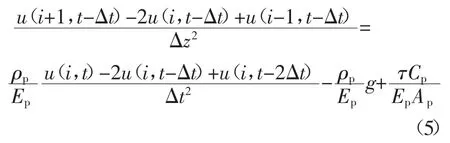
对于桩锤，设桩锤与桩顶单元间弹簧系数为kh、桩锤质量为mh、激振力为Fh、加速度为ah.若桩锤为第1 个单元、桩顶为第2 个单元，则根据受力分析，桩锤所受合力为激振力、桩锤与桩顶弹簧力和桩锤自重的和，即式（6）：

结合有限差分公式（4），得桩锤单元的控制方程差分形式见式（7）.

根据式（1），可得在时间t 时桩身第i 单元和第i+1 单元间轴力P（i，t）和桩锤与桩顶间的作用力Ph分别见式（8）和（9）.

由前文可知式（5）和（7）中Ap、Cp、Ep和ρp为桩身参数，mh、kh为桩锤参数，Δz 和Δt 为单元长度和时间增量步长，其他量或函数的确定方法如下：

1）桩头激振力Fh

振动锤内偏心轮成对且对称布置，旋转过程中产生的水平向作用力分量相互抵消，因此振动锤仅在成对偏心轮轴连线的垂直方向产生随时间呈周期性变化的激振力.令第i 个偏心质块质量为mi，偏心质块等效为质点时的旋转半径为ei，各偏心块的角速度均为ω，则可得含有n 对偏心轮的振动锤在时刻t 产生的力Fh，dyn为：

此外，桩锤另含重量为W 的配重块及桩锤自重mhg，且二者均为恒重，故桩锤可提供的激振力Fh可表示为式（11）.

2）土阻力

桩土作用力，根据作用在桩的位置不同，可分为桩侧摩阻力和桩端反力；根据力的特性可分为静阻力和动阻力，故桩土作用力包括作用在桩身上的静、动侧摩阻力和作用在桩端的静、动端阻力.关于静阻力，当前主要有理想弹塑性模型[16]、双曲线模型[34]，以及考虑非线性加载曲线的塑性模型[35]，其中应用最为广泛的是理想弹塑性模型[16]，该模型简述如下：

针对桩土作用静阻力，即桩土界面弹簧提供的力，假定桩土相互作用中静阻力与桩身位移满足理想弹塑性的关系，见图3，即土静阻力随桩土相对变形的增加而线性增加，当达到土阻力极限值后，桩土相对变形增加而土阻力保持极限土阻力值不变.令τs，ult和qb，ult分别为土体静侧摩阻力和桩端静阻力的极限值，Qs和Qb分别为桩侧和桩端静阻力达到极限值所需的位移量，见式（12）.

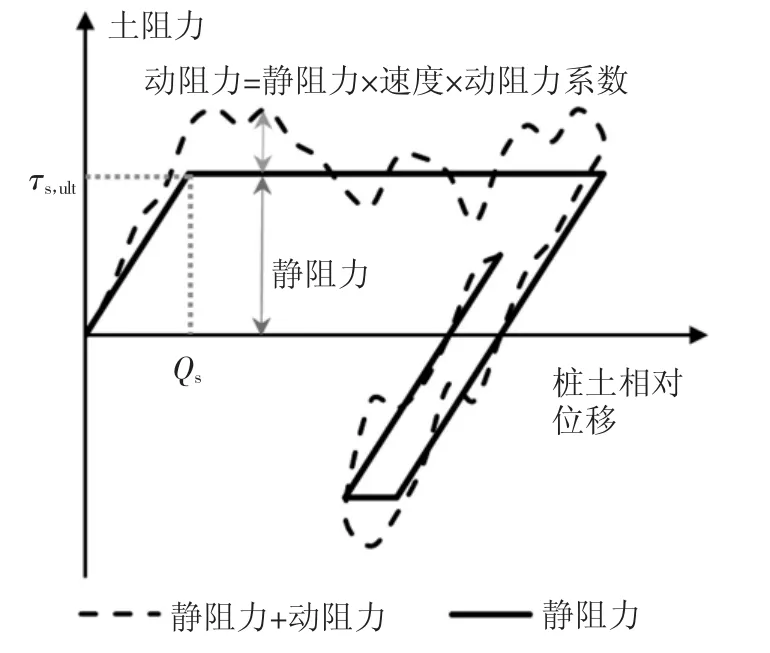
图3 土阻力模型Fig.3 Model for soil resistance

桩周土作用在桩身上的动阻力随桩土相对运动速度的增大而增大，通过阻尼器模拟，通常采用Smith[16]假定：桩侧动摩阻力和桩端动阻力等于动阻力系数J（桩侧动阻力系数Js和桩端动阻力系数Jb）、桩土相对位移速度v 和此时对应位置静阻力τs和qb的乘积，见式（13）.

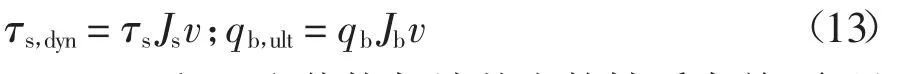
Qs、Qb、Js和Jb取值均与地基土的性质有关，参见表1.

表1 发挥极限土阻力所需位移和动阻力系数推荐值Tab.1 Recommended values for quake and dynamic factors

从图3 中可看出，一次加载中桩土弹簧弹性变形超出Qs或Qb后，若变形继续增大则桩与土之间发生滑移，此时土作用在桩身上的静阻力恒等于极限值.之后，反向卸载和再加载时，桩土界面的滑移状态立刻结束、并反向发生弹性变形，直至该反向卸载再加载位移量达到Qs或Qb时，则再次发生滑移.振动沉桩过程中桩侧与桩端的静阻力极限值τs，ult和qb，ult，见式（13），本文将基于Jardine 等[28]提出的ICP-05 方法进行估算，简述如下：

桩上某一点处的极限静侧摩阻力估算，首先令该点至桩端距离为h，该深度处CPT 试验所得锥尖阻力为qc，上覆土压力为，那么ICP 估算得此处土径向有效应力如式（14）.

式中：Pa为大气压，通常取100 kPa；R*在桩是闭口桩时取桩的半径，在桩是开口桩或其他形状（如方桩、H形桩）时取面积与桩端净截面积相同的实心圆的半径.

需要说明的是，桩土间往复作用导致的界面力学性能弱化仅与桩基贯入长度和土层深度相关，并主要通过折减对应深度处桩土间极限静阻力τs，ult模拟，见式（14）.从式（14）可看出，随着贯入深度的增大，各土层距桩端的距离h 也会增大，对应径向有效应力在超过8 倍R*后逐渐减小.进一步，在该模型中，假定达到极限摩阻力所需的位移Qs为恒值，仅与土性有关，见表1，不受往复加载的影响.因此从图3 可看出，在往复作用过程中，τs，ult减小、Qs不变时，桩土界面间剪切作用刚度也在折减.可见，该模型考虑了沉桩过程中桩土往复作用导致的界面力学性能弱化.

根据摩尔-库伦准则，设桩土界面破坏时摩擦角为δf，再结合经验系数a（对开口桩取0.9，对闭口桩取1），即可得到极限侧摩阻力τs，ult，见式（16）.

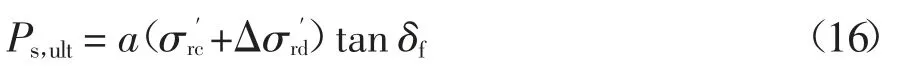
针对开口管桩和闭口桩的端阻力计算，采用了ICP-05 方法，其中对于土塞填充率IFR 为1 的开口管桩，ICP-05 方法认为端阻力为桩刺入土体所致，作用面积为管桩的净截面积，单位极限端阻力qb，ult通过式（17）计算得到.对于IFR 的确定，可以通过实际测量得到，也可根据理论或经验计算获得[38].

1.2 求解流程

基于前文建立的理论模型，求解振动沉桩过程中桩身位移与应力的具体计算步骤如下，计算流程如图4 所示.

图4 计算流程图Fig.4 Program flow chart

a）输入桩的几何尺寸及材料参数、桩锤和工作参数、土的基本性质及CPT 数据，确定Δz 和Δt 的值；初始状态下，已知桩身各单元位移u 均为0；

b）根据式（11）求得桩锤激振力，根据式（12）和（13）估算各单元所受的土阻力；

c）通过式（5）和（6）结合上一时间点各单元位移状态计算Δt 时间后的单元位移；

d）重复第b 步和第c 步，至达到设定的迭代结束条件（如时间大于设定值）.

通过上述流程即可得到振动沉桩过程中，桩身位移、应力等力学响应，从而为工程设计与施工阶段振动沉桩最大深度预测、沉桩可行性判定、桩锤型号选择、桩身疲劳损伤度验算等奠定基础.

2 算例分析

为验证本文模型，选取了文献[39]中的一高速公路与水路间钢板桩振沉案例进行计算分析.该工程位于荷兰Friesland，场地的地下水位在地表下0.5～1.0 m 处，场地主要为砂土，场地的静力触探试验结果如图5 所示.试验所沉入的钢板桩型号为AU16，其截面积为74.1 mm2，周长1.91 m，桩长20 m，根据ICP-05 方法，可得式（14）中R*为45 mm.沉桩过程中，采用的振动锤型号为PVE 2335VM，桩锤的最大偏心力矩为350 N·m，激振器最大工作频率约为38.3 Hz（2 300 r/min），桩锤和夹具质量总和为5 600 kg，配重质量为2 600 kg.本文模型计算中采用的其他参数见表2，其中桩内、外半径的确定是根据板桩与管桩的外周长和净截面积分别相等的原则，桩侧桩端动阻力系数和最大弹性变形取表1 中Smith[16]建议值，桩土界面摩擦角和Δr 参照Jardine 等[28].需要说明的是，Sinke[39]指出，在振动荷载作用下，桩侧和桩端受到的土阻力仅为CPT 试验实测的侧阻力和锥尖阻力的15%和40%.因此，本文模型计算中，土阻力取基于ICP-05 方法估算得到的摩阻力的30%.

图5 Friesland 场地锥尖阻力qc 随深度的分布[39]Fig.5 Tip resistance qc distribution with depth for Friesland[39]

表2 计算模型参数表Tab.2 Summary of model parameters

图6 给出了本文模型预测的桩基贯入速度（即单位时间内桩贯入的深度）与文献报道值的对比，可看出本文模型与求解方法得到的贯入速度曲线与原文献中报道的预测结果吻合较好，可见本文模型可以较好地预测振动沉桩的实际贯入过程.图6 中约12 m、17 m 两深度范围内桩基贯入速度的减小和图5 中的CPT 端阻力qc值减小一致，也进一步说明原位静力触探端阻力的变化能较好地反映现场沉桩过程中桩基的贯入速率.

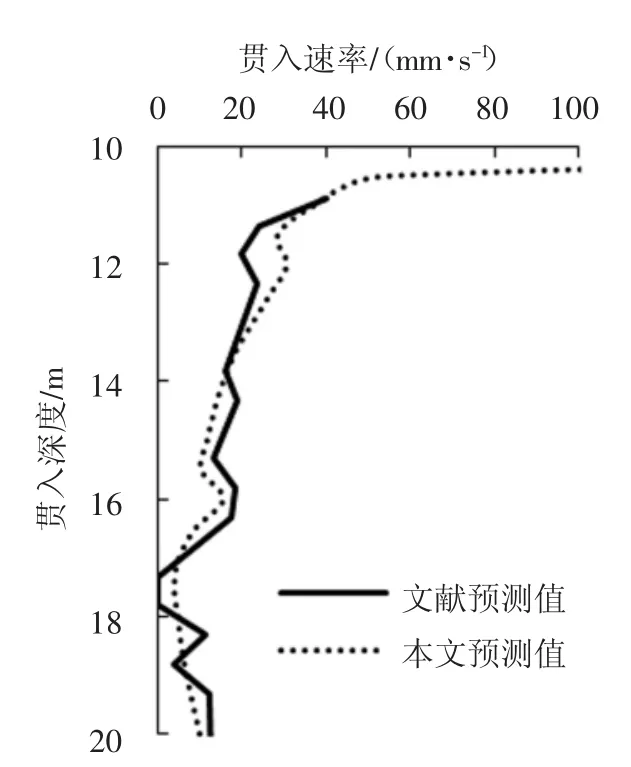
图6 桩基贯入速率对比Fig.6 Comparison of pile penetration rates

为进一步研究沉桩过程中桩身位移随时间的变化特征，本文分别取3 个深度处的桩端沉降时程曲线进行分析.如图7 所示，可看出，桩端在不同深度处时，桩端位移时程曲线周期特征均与桩锤激振力周期变化一致；随着贯入深度的增加，贯入阻力增加，无论是每个周期内的桩端位移的波动幅值，还是周期内同相位处桩端位移的增量都发生了显著减小.在贯入深度达18 m 时，ICP-05 方法确定的桩端极限静阻力为0.2 MN，桩侧极限静阻力为1.8 MN，而桩锤最大激振力为2.03 MN，与极限静阻力十分接近，桩的贯入速率明显减小，这也许是罗春雷等[40]指出的“跳机”现象产生的原因.此时，可通过调整设备运行参数以改变激振力大小，从而驱使桩基继续贯入.

图7 不同贯入深度处桩端位移随时间变化特征Fig.7 Tip displacement versus time at different penetration depths

桩基贯入过程中还有另一个不可忽视的问题，即沉桩过程桩身应力特征.图8 给出了桩基贯入过程中桩端分别在贯入深度达12 m、16 m、18 m 时桩身最大拉、压应力分布，其中压应力为正.从图8 中可看出，随贯入深度的增加，桩身最大拉压应力均呈增大趋势，最大拉应力的增加速率较最大压应力大；且随着贯入深度的增加，桩身最大拉应力值逐渐趋近于最大压应力值.桩身最大拉压应力增加原因可能是桩身内克服土阻力的部分体现为桩身拉压应力，因此，随土阻力增大，桩身内拉压应力均增大.而桩身拉应力与压应力之间差值变化的可能原因是桩所受阻力增大后，反射的拉应力波大小逐渐趋近于桩锤压应力波所致.

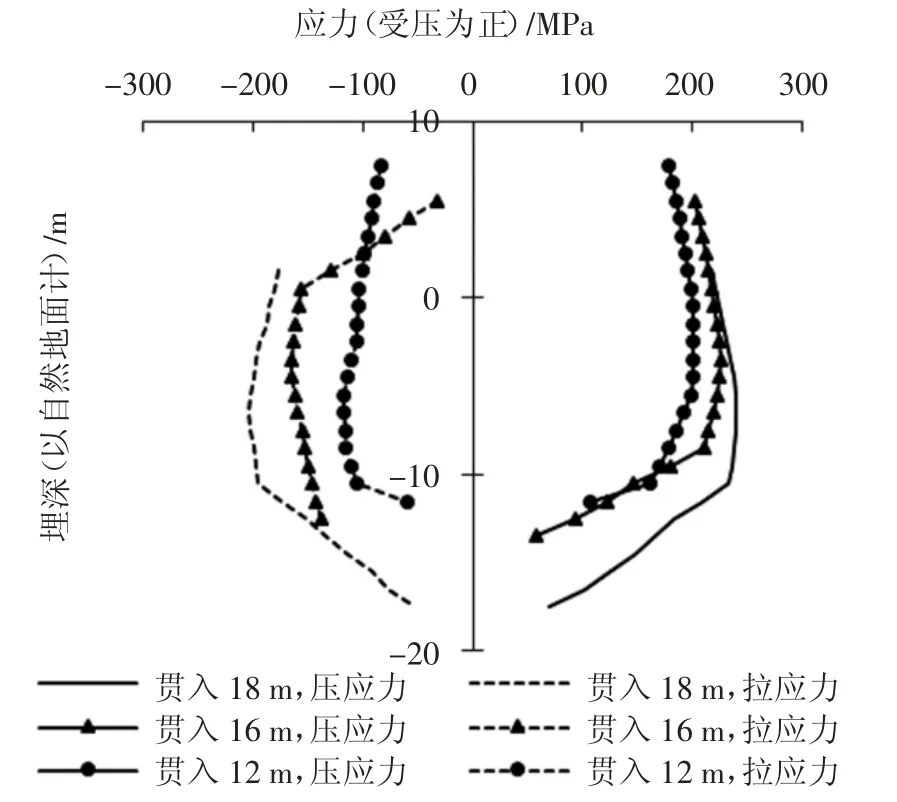
图8 不同贯入深度处桩身最大应力沿桩身的分布Fig.8 Maximum stress in pile shaft at different penetration depths

此外，最大拉应力和最大压应力呈现出在桩端部较小，在桩中上部较大的分布情况.其原因可能是桩身应力波中，由桩锤下行的波和由桩端反射上行的波主要在桩中部汇集.因此在对桩基贯入过程中桩身材料疲劳损伤评估时，可取桩身中段或中点处断面的应力大小.

3 参数分析

为进一步探讨振动锤参数对桩基贯入过程的影响规律，本文在上述案例的基础上，分别探讨了振动锤的工作频率、偏心力矩、配重对桩基贯入速率的影响.

3.1 工作频率

振动锤的激振力产生均是由动力设备驱动偏心质块引起的.为在实际工程施工过程中有效控制沉桩力，振动桩锤的工作频率可根据需要在一定范围内调整.本文首先令偏心力矩不变（350 N·m），分别研究30 Hz、40 Hz 和50 Hz 三种频率对桩基贯入速率的影响.

由图9 给出的振动锤不同工作频率对应的桩基贯入速率数据可知，当偏心力矩不变时，提高工作频率ω 会加快桩的贯入速率.当桩基自深度10 m 贯入至20 m 深度处时，振动频率为30 Hz、40 Hz 和50 Hz情况下所需的时长分别约为1 520 s、890 s 和570 s，以30 Hz 为基准，40 Hz 和50 Hz 平均贯入速率分别增加了1.7 倍和2.7 倍.导致这一现象的原因主要有两个：首先工作频率的增大会提高激振力幅值meω2，增加了驱动桩下沉的沉桩力，有效克服桩基贯入过程中的土阻力；其次，桩锤工作频率的提高有利于引起桩周土的破坏或液化，进一步降低了桩基贯入过程中所受的土阻力[41-42].

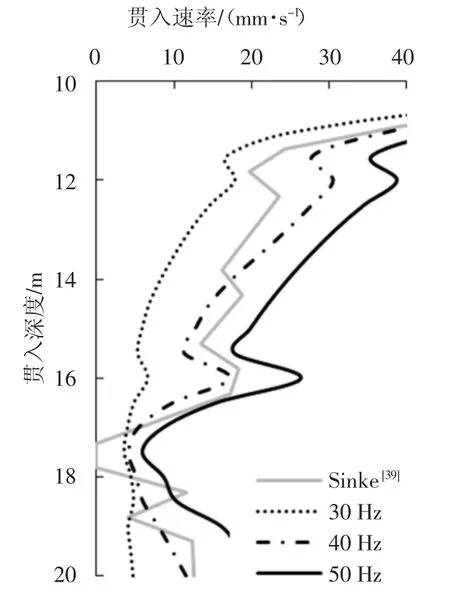
图9 工作频率对桩基贯入速率的影响Fig.9 Effect of hammer frequency on pile’s penetration rate

3.2 偏心力矩

振动桩锤的偏心构件中，可采用滑移齿轮、调节偏心块夹角、调节偏心油缸行程等方式改变偏心力矩[25].在不改变工作频率的情况下，通过改变偏心力矩而改变激振力的做法也会对桩基贯入速率造成影响.本文将分别取偏心力矩为实际值1 倍（35 kg·m）、0.5 倍（17.5 kg·m）和1.5 倍（52.5 kg·m）进行参数分析（如图10 所示），分析过程中保持桩锤的工作频率不变，为38.3 Hz.

图10 偏心力矩对沉桩速率的影响Fig.10 Effect of eccentric motion on pile’s penetration rate

由图9 给出的不同偏心力矩对应的桩基贯入速率计算结果可知，当桩基贯入深度从10 m 至20 m时，0.5 倍、1 倍和1.5 倍偏心力矩所需时间分别为约3 300 s、970 s 和320 s，1 倍和1.5 倍偏心矩下的平均贯入速率是0.5 倍偏心矩下的3.1 倍和10.4 倍.可见，偏心力矩改变对桩基贯入速率的影响较为明显.产生这一现象的主要原因为提高偏心力矩会增大激振力幅值，使桩在克服土阻力后引起下沉的合力增大，从而加速了桩的贯入.这一点与偏心力矩不变而改变工作频率时的计算结果相似，因此提高激振力也是一种能够有效提高沉桩效率的方法.

3.3 配重

实际工程施工中，除了偏心轮旋转产生的大小随时间周期性变化的沉桩力，还有除振动锤构件自重外另配的质量块，见式（11）.案例[39]中所用配重质量为2 600 kg，本文将分别对无配重（0 kg）、1 倍配重（2 600 kg，相当于激振力幅值的1.3%）、5 倍配重（13 000 kg，相当于激振力幅值的6.3%）和10 倍配重（26 000 kg，相当于激振力幅值的12.6%）下的贯入速率进行计算分析.

从图11 中给出的不同配重质量对应的桩基贯入速率数据可看出，不同配重大小对应的贯入速率不同，贯入速率基本呈现随着配重的增大而增大的规律，即配重为最大激振力的0%、1.3%、6.5%和12.6%时，所需贯入时间分别约为1 030 s、970 s、780 s 和600 s.需要说明的是，无配重（配重为0 kg）与配重仅为激振力1.3%时贯入速率基本一致，而配重达到激振力6.3%之后，配重的增加才能较为明显地增大贯入速率，如增加配重至激振力幅值6.3%时，桩基贯入速率增加25%.这也就是说，若采用增加配重的形式提升桩锤成桩能力，需将配重增加到一定的量.然而，正如前述，振动锤以轻巧为振动沉桩工艺的一个优点，大量增加配重不但使该工艺优势减小，也对起吊设备提出了更高的要求，因此不建议采用增大配重的方式加快桩基贯入速率.这也是为什么在现场施工时，遇到桩基不能被沉至设计标高时，仅仅在原配重块的基础上增加不超过3 000 kg 的配重，对沉桩速率或贯入深度仍无明显的改变.

图11 配重对沉桩速率的影响Fig.11 Effect of additional weight on pile’s penetration rate

4 结论

针对振动沉桩过程的预测，本文基于一维波动方程及原位静力触探试验结果，建立了桩基贯入过程的理论分析模型，编制了对应的计算程序，并通过实际工程案例进行了讨论分析，验证了本文理论与程序.在此基础上，针对施工过程中振动锤的工作频率、偏心力矩及配重等参数对桩基贯入速率的影响展开了讨论，得到如下主要结论：

1）基于针对桩基静承载力预测的ICP-05 方法进行振动沉桩贯入过程中桩基受到的土阻力预测，可以较好地估算桩基在贯入过程中的响应.

2）随着桩基贯入深度的增加，桩身各处拉、压应力均呈增大趋势.其中，在贯入深度较小时桩身各深度处拉应力明显小于压应力，而随着贯入深度的增加，拉应力绝对值大小逐渐趋近于压应力的绝对值.而拉、压应力基本呈现桩头桩端较小，中间段较大的分布特征，因此，在验算桩基贯入过程中疲劳损伤时，可取桩身中段或中点的应力进行计算分析.

3）通过调整振动锤工作频率和偏心矩可有效改变沉桩速率，如振动锤工作频率由30 Hz 提高67%时，平均贯入速率可提高170%；桩锤偏心矩由35 kg·m 提高50%，平均贯入速率可提高240%；尽管配重的增加有助于提高桩基贯入速率或设备沉桩能力，但远低于改变工作频率和偏心力矩所产生的效果，且考虑到该工艺的优势及对起吊设备的要求，不建议通过增加配重的方式提升设备沉桩能力或沉桩速率.