考虑孔壁粗糙体退化的灌注桩竖向荷载传递

刘亚楠，赵衡，赵明华，彭文哲

（湖南大学 岩土工程研究所，湖南 长沙 410082）

在我国南方山区，常采用半路半桥或公路桥梁的形式跨越山区或峡谷，此时需将桥梁桩基设置在风化程度各异的土层或岩层中[1].在各类地层的钻孔和成桩过程中，扰动的地层与浇筑的混凝土桩体之间会形成参差不齐的剪切面.当基桩承受竖向荷载时，由于剪切面的错动引起的界面摩擦是桩侧阻力的主要来源[2].目前，国内外众多学者基于室内模型试验及现场试验结果，建立了大量理论模型预测钻孔灌注桩的桩侧摩阻力发挥机制[3-5].但是，这些研究大都基于各种数学假定而缺乏对应的物理机制.例如，假定摩阻力的发挥与相对剪切位移之间服从线性、双曲线或者三折线的数学关系.这类模型本质上属于半经验半数学方法，需根据经验参数完善模型参数的选取，最终确定侧阻力极限值.

20 世纪60 年代，Patton[6]基于室内岩石直剪试验结果提出了经典的Patton 节理模型，首次将岩石节理假定为一系列规则的三角形粗糙体，并给出了峰值抗剪强度的双折线包络线.随后，Ladanyi 等[7]从能量耗散的角度对Patton 模型进行了改进，以考虑被剪断的粗糙体所能提供的残余摩擦力.针对岩石节理的随机性与不规则性，Barton[8]提出了著名的JRC（The Joint Roughness Coefficient，粗糙度系数）-JCS（The Joint Wall Compressive Strength，节理壁面抗压强度）模型，引入10 条标准轮廓线来反映不同二维岩石节理面的JRC.然而，Grasselli 等[9]在研究粗糙度和材料特性对节理剪切变形行为的影响时发现，当界面剪切的相对位移越大时，剪切过程中节理自身的压缩变形与磨损就越大.显然，节理剪切过程中的剪胀角i 并非恒定值，而是与材料性质参数和几何参数相关的变量.Patton 剪切模型形式简单且参数具有显著的物理意义，为预测钻孔灌注桩的桩侧摩阻力发挥提供了新的思路[10-15].但值得注意的是，Patton剪切模型是基于刚性粗糙体的概念进行建模的，换言之，对于灌注桩的孔壁粗糙体，需要进一步考虑桩身混凝土和孔壁地层的相对刚度[16-18].当刚度较大时，地层粗糙体的压缩与退化效应不容忽视，且将进一步影响粗糙体的抗剪强度.这是由于在剪切位移的发展过程中，孔壁对桩身的侧向约束程度将随着界面剪胀的增加而增加[16，19-20].因此，不考虑粗糙体的压缩将高估界面的剪胀程度和孔壁的侧向约束程度.对于工程设计来说，这种高估无疑是偏于不安全的.

基于此，本文考虑到孔壁地层与桩身混凝土的相对刚度差，引入了一个粗糙体退化系数来定义在剪切过程中所产生的粗糙体表面磨损及体积压缩的行为.在此基础上修正了经典的Patton 节理模型，并用以描述灌注桩的侧阻力发挥机制.然后，将其引入灌注桩的竖向荷载传递分析中，并推导基桩轴力与沉降之间的关系.最后，通过算例验证，证明了本文理论计算方法的可行性，并对粗糙体半波长及倾角的影响进行参数分析，以期为灌注桩的初步设计提供一定的参考.

1 常法向刚度条件下桩侧摩阻力

1.1 基本假定

钻孔灌注桩成孔时，桩身混凝土与孔壁地层的交界面将存在由于钻孔设备钻进而产生的粗糙体，当该界面滑移时，会出现滑移剪胀现象（如图1 所示），界面的法向应力增加，嵌岩段桩侧摩阻力的产生主要由此引起.

为便于后续理论推导，本文做如下假定：1）桩岩界面的粗糙体为规则等腰三角形，半波长为λ，粗糙体倾角为β（见图1）；2）忽略界面的胶结作用力cu；3）孔壁地层材料的刚度小于桩身混凝土.

图1 钻孔灌注桩滑移剪胀过程Fig.1 Sliding-dilation process of cast-in-place piles

1.2 法向应力及法向刚度

钻孔灌注桩工作过程中，桩身在荷载作用下与孔壁地层发生相对向下的位移，将产生沉降w.界面发生剪胀，产生法向应力增量，根据厚壁圆筒的弹性理论解，当洞壁发生径向扩张时（轴对称）的法向应力增量Δσn为：

式中：Er为岩体的弹性模量；νr为岩石的泊松比；r 为桩截面半径；Δr 为桩半径增量.

令K=Er/（（1+νr）×Δr），将其定义为围岩法向刚度，可知法向应力增量Δσn与径向扩张线性相关.当深度z 处界面的相对位移增量为Δw，孔壁粗糙体处于弹性状态时，岩壁的径向膨胀为：

式中：β 为粗糙体倾角.

根据式（1），法向应力增量为：

1.3 粗糙体压缩

在初始剪胀过程中，剪胀角i 可视为粗糙体倾角β，即初始剪胀角i0=β.然而，常法向刚度（Constant Normal Stiffness，CNS）条件下法向应力的施加可能导致粗糙体的压缩与磨损（本文统称为退化），粗糙体倾角的退化过程可通过粗糙体高度的降低来表征[15]，如图2 所示.

图2 粗糙体变形示意图[15]Fig.2 Schematic diagram of asperity deformations[15]

显然，不同法向应力会产生不同的粗糙体压缩高度Δy，从而直接影响剪胀角的发挥程度.受法向应力和法向刚度的影响，粗糙体的退化将不会与剪切位移线性相关.因此，剪胀角不能直接使用粗糙体初始剪胀角i0，而应由动态变化剪胀角i 来代替.此时，倾斜率tan i 可用于衡量剪胀角发挥值，表示为：

1.4 桩侧摩阻力表达式

一般而言，软岩粗糙体的压缩程度太大而不能被忽略，滑移剪胀过程中，剪胀角发挥值i 小于初始剪胀角i0.鉴于此，本文引入退化因子η 来表征瞬时剪胀角与初始剪胀角的比值，如式（5）所示.η=0，对应粗糙体未退化条件；η=1，对应粗糙体被完全破坏条件.

式（5）为粗糙体退化的一般关系，但退化规律的演变不能简单地用此方程来表征.大量直剪试验[9-11]表明：剪胀角的退化速度随着剪切位移的增加而下降；在大多数情况下，其变化曲线可用指数函数描述.在此基础上，本文通过定义两个参数的幂函数来描述粗糙体退化特性，如式（6）所示.

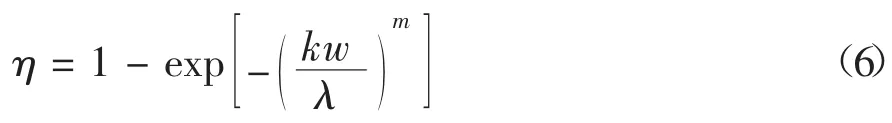
式中：λ 为粗糙体半波长；m 为材料参数；k 为几何参数.目前尚不清楚m、k 与其他物理力学参数（如软岩抗压强度或杨氏模量）之间的关系，但可以确定的是，m 与岩石抗压强度成正比，k 与粗糙度成正比.

滑动剪切力S 可以表示为：

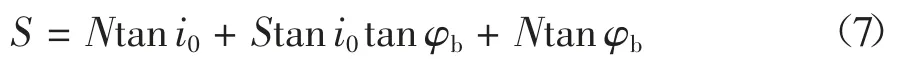
式中：N 为法向力；φb为软岩内摩擦角；Ntan i0，Stan i0tan φb，Ntan φb分别表示由法向力抵抗剪胀的滑动摩擦力、剪胀时引起额外的滑动摩擦力以及不考虑剪胀时内摩擦角引起的滑动剪切力.

相应地，其滑动机制可表示为：

式中：τ 为剪切应力.

常法向荷载条件下规则三角形粗糙体的峰值抗剪强度可由经典的Patton 模型[6]表示：

式中：σn为法向应力；φr为软岩的残余摩擦角；c 为黏聚力；σT为过渡应力，σT=c/[tan（φb+i）-tan φr].

将式（7）和（8）代入式（9），桩岩界面平均剪切应力可通过剪胀角来计算。

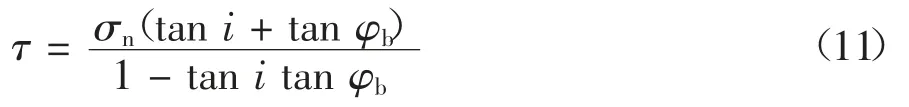
在CNS 条件下，施加的法向应力通常由以下两个分量组成：初始法向应力σn0以及由剪胀引起的应力增量Ky，即σn=σn0+Ky=σn0+Kw tan i，其中K 是法向刚度.则式（11）可改写为

因此，CNS 条件下的τ-w 表达式为：

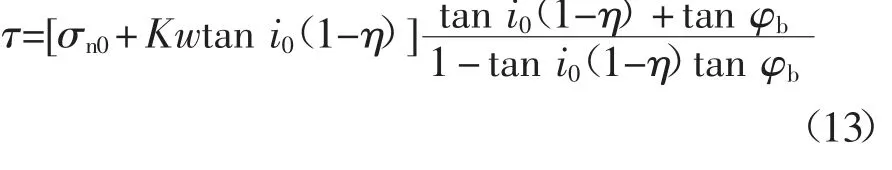
2 桩身沉降及轴力计算

2.1 基本微分方程的建立

根据荷载传递理论，对桩身任一截面有：

式中：U 为灌注桩的周长；Ap为灌注桩的截面积；Ep为灌注桩的弹性模量.

结合τ-w 曲线可知，式（14）难以得到解析解，故本文使用有限差分法对其进行求解，并根据τ-w 曲线的变化趋势，采用二次多项式对其进行拟合，便于简化差分求解过程.故式（14）可写作：

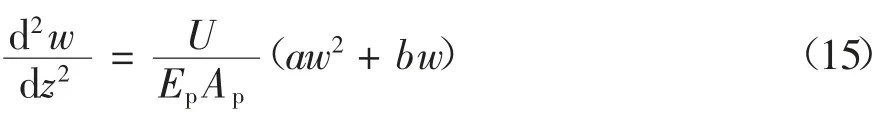
式中：a，b 分别为τ-w 曲线的二次多项式拟合式中二次项与一次项常系数.

2.2 基本微分方程的求解

自桩顶至桩底将全桩分成N 分段，各节点编号i分别记为0，1，…，K，…，N-1，N，并在桩顶和桩底分别增加1 个虚拟节点，表示桩顶及桩底处沉降（如图3 所示），其中N 为桩底处节点编号.

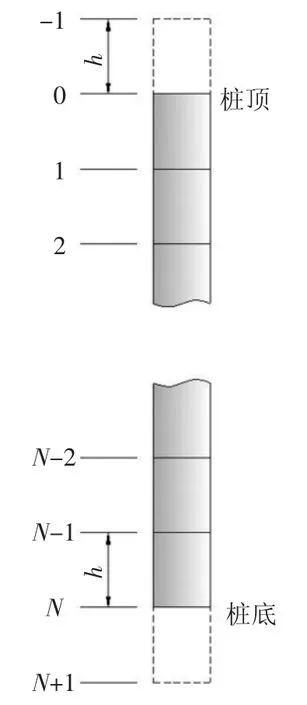
图3 基桩差分节点Fig.3 Differential points of pile

相邻节点之间的距离为h=dz，对于第i 个节点，式（14）可推导为差分形式：

即任意节点沉降可由相邻两节点沉降表示：

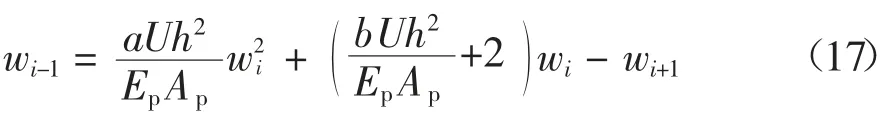
对于节点N，式（17）可写为：

对于节点N-1，式（17）可写为：

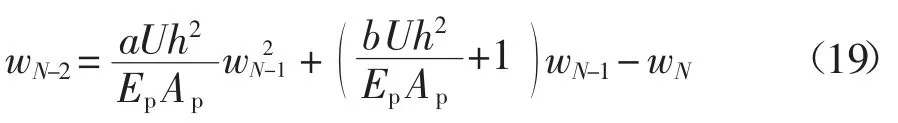
显然，可依次推导出相邻3 个节点沉降之间的关系.

对于桩顶，可根据现场实测轴力所对应的沉降值wp，取w0=wp作为边界条件，因此对于节点0，式（17）可写为：

对于上述方程可使用迭代法，由节点1 递推至节点N，控制边界条件w0=wp，得到w1依次递推各节点沉降，然后将wi代入式（17），即可求解节点i 处桩侧摩阻力，进而获得桩身轴力变化曲线.

3 算例验证

为了验证本文方法的可行性，引入O′neill 等[21]的钻孔桩现场静载试验进行对比.试验场地的岩层条件如下：上层为3 m 的填土，下层约为6 m 的泥页岩.桩身嵌岩深度为6.1 m，基桩直径为0.61 m，桩身混凝土重度为20.4 kN/m3，其弹性模量Ep为2.761 04 MPa，取围岩平均弹性模量Er为232 MPa，岩层内摩擦角为24.8°，黏聚力为1.2 MPa，结构面摩擦角φu为30°，残余内摩擦角φr为24°，泊松比νr取0.25，泊松比为0.3，剪胀角i 为10°，半波长λ 为10 mm，m=4.62，k=0.94.根据以上参数，采用本文方法计算桩身轴力变化曲线，并将其与实测曲线进行对比，如图4 所示.由图4 可知，本文理论方法计算获得的桩身轴力变化曲线与文献[21]的实测曲线趋势一致，吻合较好，说明本文方法可用于分析灌注桩荷载传递机制.

图4 理论预测曲线与现场实测值对比Fig.4 Comparison of theoretical prediction curve and field measured value

4 参数分析

通过上述分析可知，粗糙体半波长λ 和倾角β是桩-岩界面剪切特性的主要影响因素.因此，本文在验证理论方法的基础上，基于控制变量法，探讨二者单独变化对桩身沉降及轴力的影响.

4.1 半波长λ 的影响

由式（6）和式（13）可知，钻孔灌注桩竖向荷载传递将受到半波长λ 的影响，因此本文假定半波长λ为某一合理的数值，对灌注桩桩身轴力随半波长λ的变化而改变的规律作一定的讨论.参数分析中其他参数保持不变，与实例验证一致，半波长λ 在8 mm、10 mm、12 mm 和14 mm 变化.分析结果如图5所示，由图5 可知，随着半波长λ 的增大，轴力下降的幅度逐渐减小，这说明桩侧界面的抗剪强度越大，桩顶竖向荷载传递的有效深度越短，反之越大.

图5 半波长对竖向荷载传递的影响Fig.5 Influence of half-wave length on vertical load transfer

4.2 粗糙体倾角β 的影响

由式（13）可知，钻孔灌注桩竖向荷载传递将受到粗糙体倾角β 的影响，因此本文假定粗糙体倾角β为某一合理的数值，对灌注桩桩身轴力随粗糙体倾角β 的变化而改变的规律作一定的讨论.参数分析中其他参数保持不变，与实例验证一致，粗糙体倾角β 在8°、10°、12°和14°变化.分析结果如图6 所示，由图6 可知，随着粗糙体倾角β 的增大，轴力下降的幅度逐渐减小，这说明桩-岩界面抗剪能力越大，桩顶竖向荷载传递的有效深度越短，反之越大.

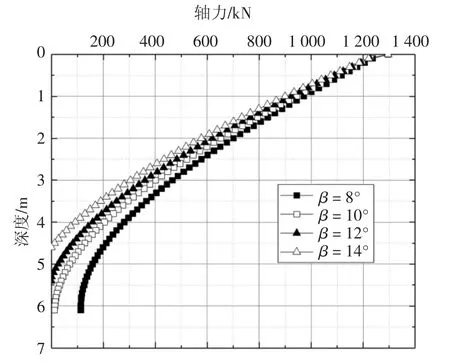
图6 粗糙体倾角对竖向荷载传递的影响Fig.6 Influence of dilatancy angle on vertical load transfer

5 结论

根据桩身混凝土-软岩界面的剪切特性，探讨了常法向刚度条件下的桩侧摩阻力发挥机制，通过考虑桩-岩界面剪胀效应，引入退化因子、材料参数和几何参数，研究粗糙体对灌注桩侧阻力及轴力分布规律的影响，得出如下结论：

1）灌注桩-软岩界面粗糙体的存在，使得桩侧摩阻力发挥机制与一般预制桩完全不同，故其工程设计难以照搬常规竖向受荷桩设计计算方法.

2）通过现场试验对比可知，本文方法所得的桩身轴力预测曲线与现场实测曲线趋势一致，说明本文计算方法用于软岩灌注桩设计计算是可行的.

3）提出一个综合考虑退化因子η，材料参数m及几何参数k 的桩侧摩阻力表达式，用以考虑粗糙体的影响，其参数可作为灌注桩承载特性的控制指标.