基于机器视觉的圆柱直齿轮齿距偏差检测技术研究
2021-12-01邰承岳袁鹏哲张烈山
邰承岳,袁鹏哲,钟 晨,刘 璞,张烈山
(浙江理工大学 机械与自动控制学院,杭州 310018)
0 引言
机器视觉技术融合了人工智能、几何光学、电子学、计算机图像学、信息处理、机器学习等学科技术,具有精度高、可靠性强、速度快、非接触式等优点。随着工业自动化的发展,特别是智能制造技术的发展,机器视觉的应用在工业生产中得到广泛的应用,在交通、医疗、农业等领域,机器视觉检测方法取代人工检测的方法已经成为明显一种趋势[1-3]。20世纪50年代,机器视觉技术诞生,由David Marr对机器视觉的理论体系进行了初步的完善。国内学者研究技术是从20世纪80年代中期才开始的,在90年代机器视觉技术才开始得到应用,21世纪,机器视觉市场得到爆发式增长,机器视觉大量应用在互联网以及工业生产中,在机器视觉方面中国即使在世界范围内也是十分活跃的[4],然而中国与机器视觉的世界先进水平仍有较大差距。
20世纪60年代,美国就已经开始在制造业应用机器视觉影像测量技术,随后,德国、加拿大、日本等国家也开始了对机器视觉影像测量相关理论及技术的研究 ,而在中国,有关影像测量的研究是从80年代开始、90年代才得到重视,虽然在机器视觉测量技术的理论模型、实验分析、系统建立等方面有了很多成果,但水平依然相对比较落后。目前,视觉影像测量技术的应用主要涉及到钢板表面缺陷检测、汽车制造质量检测、印刷质量检测、齿轮参数检测等测量领域中[5-9]。
一些接触式设备如三坐标测量机、专用测量尺规等工具目前仍然是主要普及的齿轮参数测量设备,这些设备操作复杂、人工和管理成本大、测量效率低、测量精度不高,逐渐不能满足工业应用生产对产品质量越来越高的要求。为了实现齿轮几何参数的高精度、自动化测量,本文以齿距偏差自动测量为例研究了一种基于机器视觉的测量方法。
1 测量原理
如图1所示,影像测量法的基本原理是先通过成像系统将被测物面成像至光电检测单元(相机感光面),光电检测单元将光信号转换为电信号(电子图片),然后将电信号传输到上位机中。上位机在获得被测物体图像后,利用图像处理软件从检测图像中提取出所需的几何特征,在根据成像系统的数学模型,计算出关心的几何量,从而实现被测产品几何参数的测量。
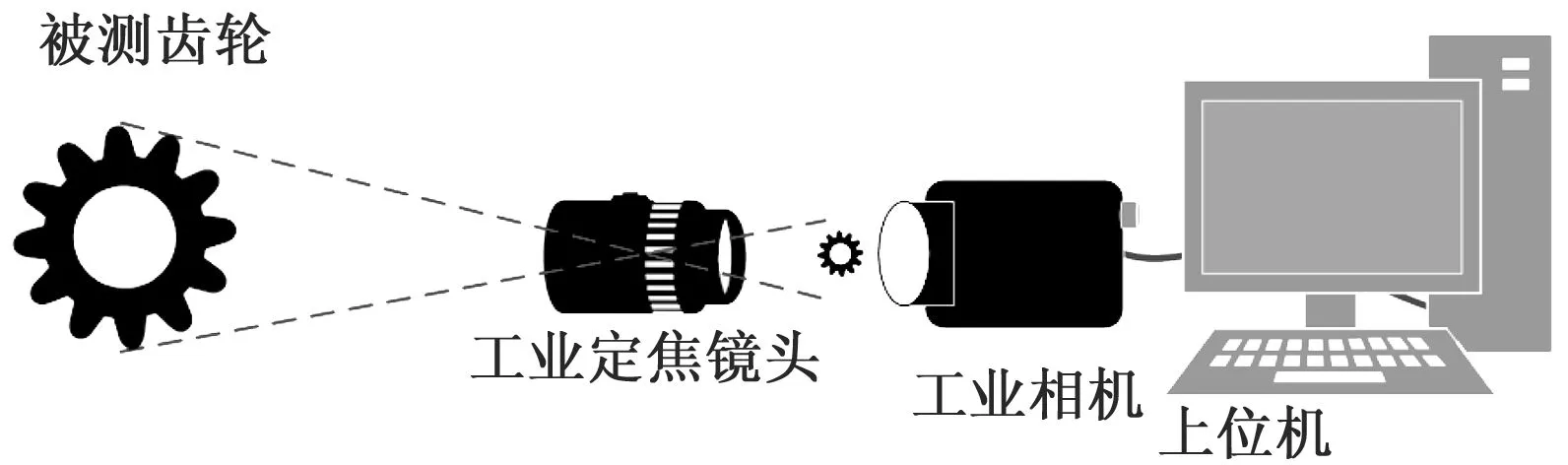
图1 影像测量法基本原理示意图
以点到点距离值的测量为例,简述影像测量法实现几何量测量的基本数学原理,利用图像采集系统获得的图片的大小为a×b,单位为:pix*pix。如图2所示,检测图像中点A和B是有齿轮轮廓与分度圆的交点,计算A、B两点间的分度圆圆弧长度。记A的像素坐标为(ua,va),B的像素坐标为(ub,vb)。
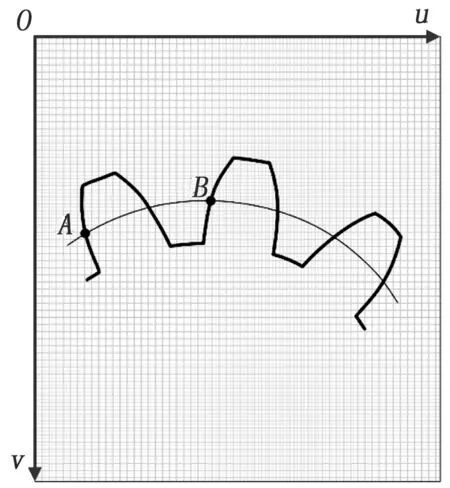
图2 几何参数测量计算原理图
设被测齿轮分度圆直径为Dp,则弧长AB的实际几何尺寸等于成像系统像素当量τ与AB像素弧长的乘积,也即:
(1)
式中,τ为像素当量,单位为mm/pix,它表示单位像素距离对应被测物面的实际几何距离,它反映的是成像系统的放大倍率,一般通过系统标定来确定像素当量的大小。对于单目影像测量系统来说,成像系统的工作距离一定,成像系统的放大倍率也不会改变,像素当量τ容易通过标准棋盘格或者标准刻度尺来实现标定。
2 测量算法设计
利用成像系统和工业相机获取检测图像后需要经过系列的图像处理算法才能最终提取出被测齿距。这些处理算法主要有:图像预处理算法、成像系统标定、齿轮轮廓及特征提取算法、分度圆构造及齿距参数测量计算算法[10-11]等。
2.1 图像预处理算法
图像预处理算法的作用是对图像进行去噪,通过二值化处理、边缘检测等一系列操作,突出测齿轮的轮廓特征,这将易于后续的算法处理。如图3所示为图像预处理算法所用的流程。
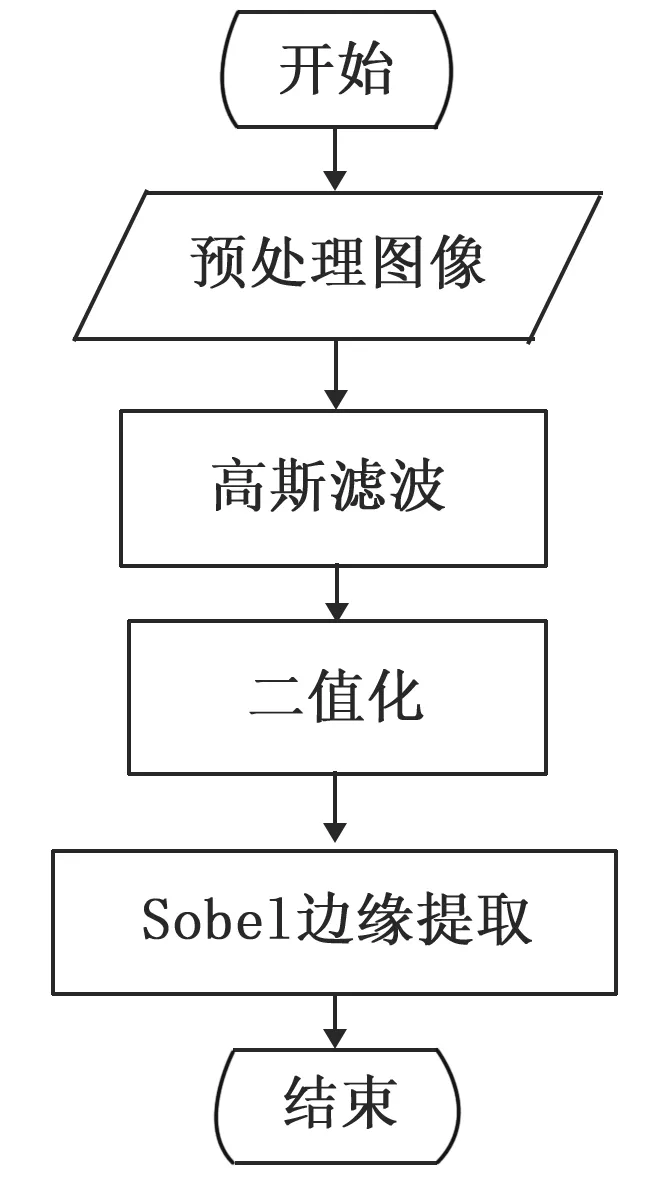
图3 图像预处理算法流程图
由于光源质量、环境杂光等因素的影响,被测图像总是存在一定的噪声点,本文采用高斯滤波实现噪点的滤除。根据背景像素值和轮廓像素值之间的差异,合理设置阈值进行图像的二值化处理,这样做能够显著突出被测齿轮的轮廓特征,滤除无用图像信息而突出有用信息,实现图像信息的降维。
2.2 成像系统标定
本文根据1998年张正友教授提出的单平面棋盘格的摄像机标定方法[12-14]编写标定算法。
2.2.1 图像畸变及矫正
实际的使用中,由于透镜制作和安装存在不确定性,摄像机的透镜总是在成像的边缘处产生较为明显的畸变,而且从机械方面也难以保证透镜和成像平面保持平行,从而产生了如图4所示的径向畸变和切向畸变。
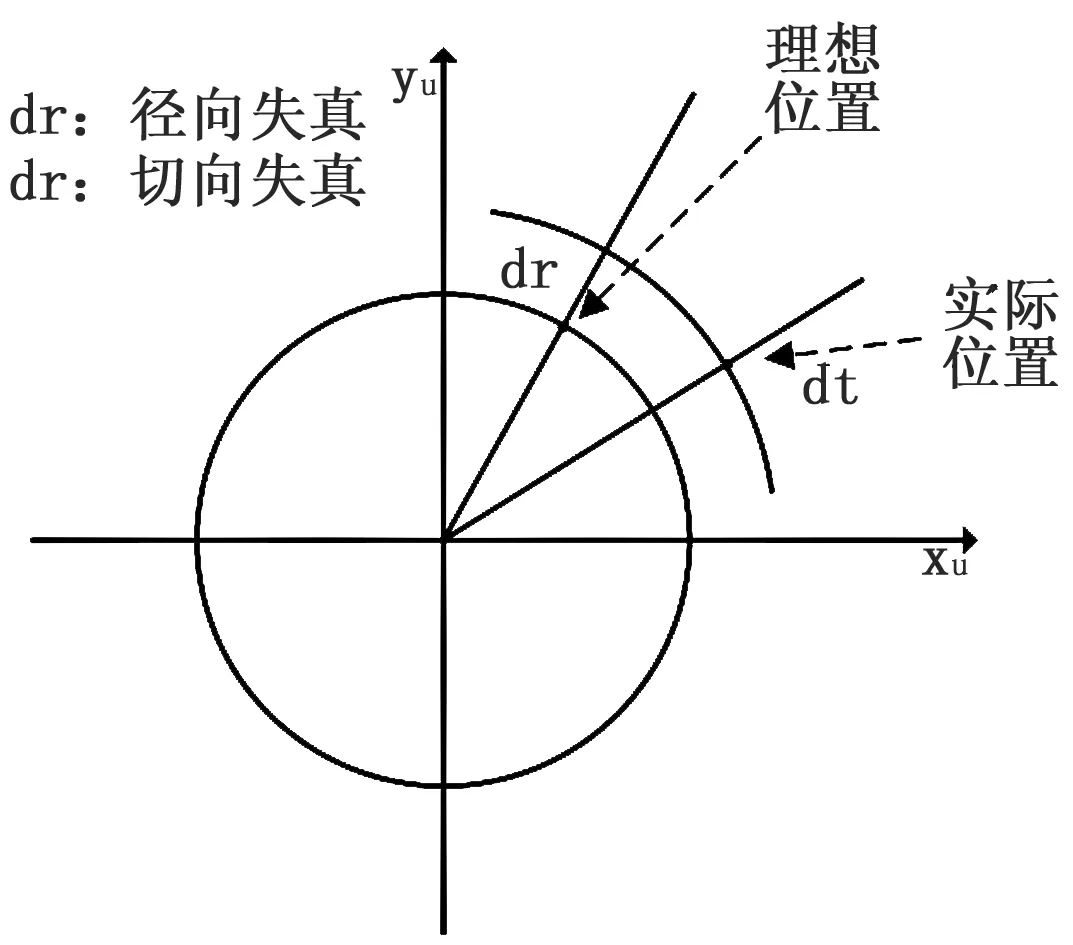
图4 相机畸变模型
在径向畸变中,可以认为光学中心没有任何的畸变,但随着半径的增大,畸变程度也随之变大,其通过泰勒级数展开进行校正:
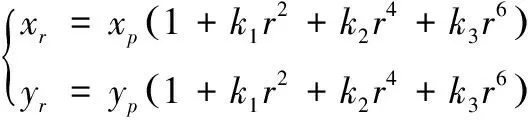
(2)
式中,xr,yr为矫正后的坐标;xp,yp为矫正前的坐标;r为与光学中心的距离;k1,k2,k3为径向畸变系数。
切向畸变的成因是透镜和焦平面不平行,存在角度α,其通过泰勒级数展开进行校正:

(3)
式中,p1,p2为切向畸变系数。
综上,我们一共需要得到5个畸变参数(径向畸变系数:k1、k2、k3和切向畸变系数:p1、p2)对图像进行畸变矫正。
2.2.2 像素当量标定
在基于机器视觉测量圆柱直齿轮齿距偏差的过程中,需要知道像素尺寸与实际尺寸的对应关系,这种关系用像素当量表示。由棋盘格标定算法我们可以得到内参矩阵M:
(4)
在内参矩阵M中,(u0,v0)为像素坐标系原点在图像坐标系下的坐标,dx、dy为每个像素点在图像坐标系x轴、y轴方向的尺寸,f为焦距。通过对内参矩阵M中元素fx、fy除以焦距f后求其倒数我们就能得到单个像素格长宽所对应实际距离的,即像素当量。
2.3 齿轮轮廓及特征提取算法
本文先对图像进行二值化和膨胀腐蚀,使得被测齿轮的轮廓特征更加突出,然后利用Sobel边缘检测算法[15-16]实现齿轮边缘的提取,保证了轮廓提取的效率和精度。
Sobel算子是一种离散性差分算子,用来运算图像亮度函数的梯度之近似值。在图像的任何一点使用此算子,将会产生对应的梯度矢量,其利用像素的周围领域的灰度加权算法,根据在边缘点处达到极值这一原理进行边缘检测,如图5所示。
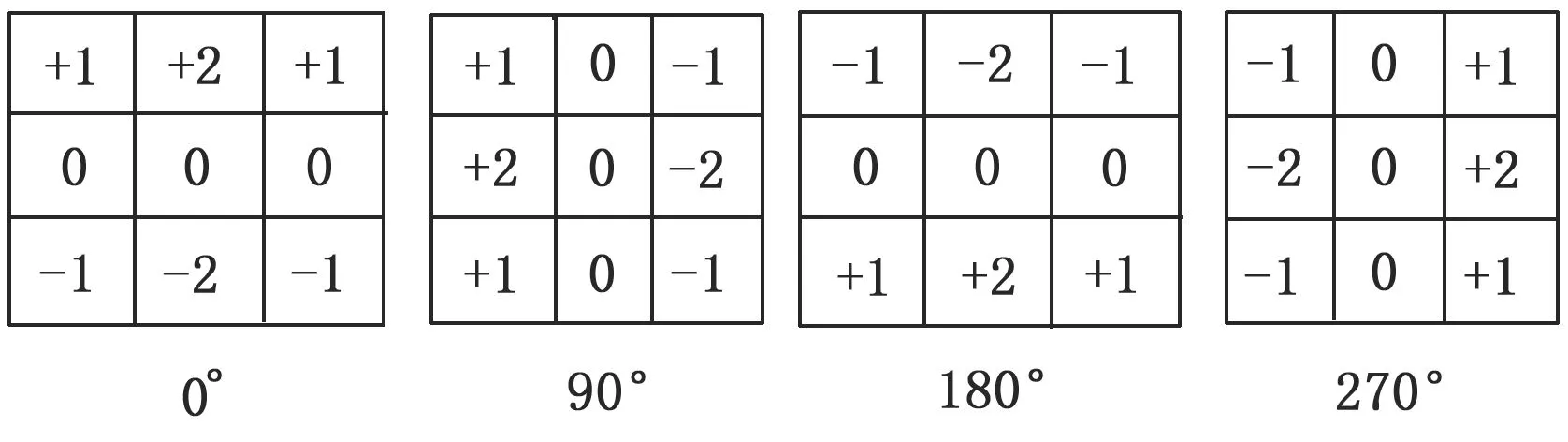
图5 Sobel算法边缘检测示意图
以常见的水平和竖直方向的Sobel算子为例,水平方向与竖直方向偏导数计算方法为:
(5)
(6)
计算像素点P5的水平方向与竖直方向偏导数公式为:
P5x=(P3-P1)+2·(P6-P4)+(P9-P7)
(7)
P5y=(P7-P1)+2·(P8-P2)+(P9-P3)
(8)
2.4 分度圆构造
分度圆的构造需要知道它的半径和中点位置,一般来说,它的中点位置应当与齿轮的中心相同。求解分度圆的半径的公式如下:
d=mz/2
(9)
式中,m为齿轮模数,z为齿数。
因此,求解分度圆需要知道齿轮的几何参数,通过图像处理相关算法计算出齿顶圆和齿根圆,根据分度圆与它们的关系求出分度圆的相关参数。求解构造分度圆相关参数的流程图如图6所示。

图6 分度圆构造流程图
1)齿轮中心(x0,y0):
齿轮中心即圆心,齿轮的圆心包括齿顶圆圆心、齿根圆圆心、节圆圆心等,本文忽略加工工艺等不可避免的问题带来的极小误差,取齿轮外轮廓拟合圆圆心、内轮廓拟合圆圆心的平均值作为齿轮的中心。
对检测出的齿轮外轮廓和内轮廓分别进行圆的拟合,通过拟合圆算法可以求出拟合圆的圆心和半径。拟合圆的算法有很多,如平均值法,加权平均值法等,其中,使用最小二值法能够简单且比较准确的拟合出想要的圆。
2)齿顶圆半径ra:
对于齿顶圆半径的求解,本文通过构建齿轮外轮廓的凸包结构,将外轮廓的轮廓点全部包含进去。
一般来说,可以将外轮廓与构建的凸包的多个交点视为齿顶圆上的点,在每个交点及其周围轮廓点都近似视作齿顶圆上的点,求得它们到齿轮中心的距离,取它们的平均值为齿顶圆半径。
3)齿根圆半径rf:
对于齿根圆半径的求解,本文先求出外轮廓点与齿轮中心的距离,得出最小距离dmin,找出外轮廓中距齿轮中心在区间[dmin,dmin+d]的点,其中d为前文求解齿顶圆时交点及其周围轮廓点到齿轮中心的距离的区间长度。同理,得到的所有轮廓点近似视作齿根圆上的点,求得它们到齿轮中心的距离,取它们的平均值为齿根圆半径。
4)齿数z:
本文采用切割法求解齿轮齿数。以齿轮中心为圆心,齿顶圆半径与齿根圆半径的平均值为半径作圆,对齿轮外轮廓进行切割,得到多个交点,对交点进行计数,得到的数值为齿数的两倍。
5)模数m:
测量仪器无法直接测量出齿轮模数,图像上也找不到相关的特征点来求解,因此需要通过已测得的齿轮参数与齿轮模数之间的数学关系来求的齿轮模数,通常可以通过查找齿轮模数系列表来确定齿轮模数,优先选择第一系列作为标准值。首先通过公式(10)计算得到m′,在从齿轮模数系列表找出与它最接近的标准齿轮模数。
(10)
2.5 齿距参数测量计算算法
根据求得的模数和齿轮齿数可以求得分度圆半径r=mz/2,以齿轮中心为圆心,作分度圆,使分度圆与齿轮轮廓相交,得到交点数组,把它们作为特征点进行分析,可以得到齿距偏差。齿距偏差主要有3个部分组成,分别是单个齿距偏差、k个齿距累积偏差、齿距累积总偏差。具体流程如图7所示。
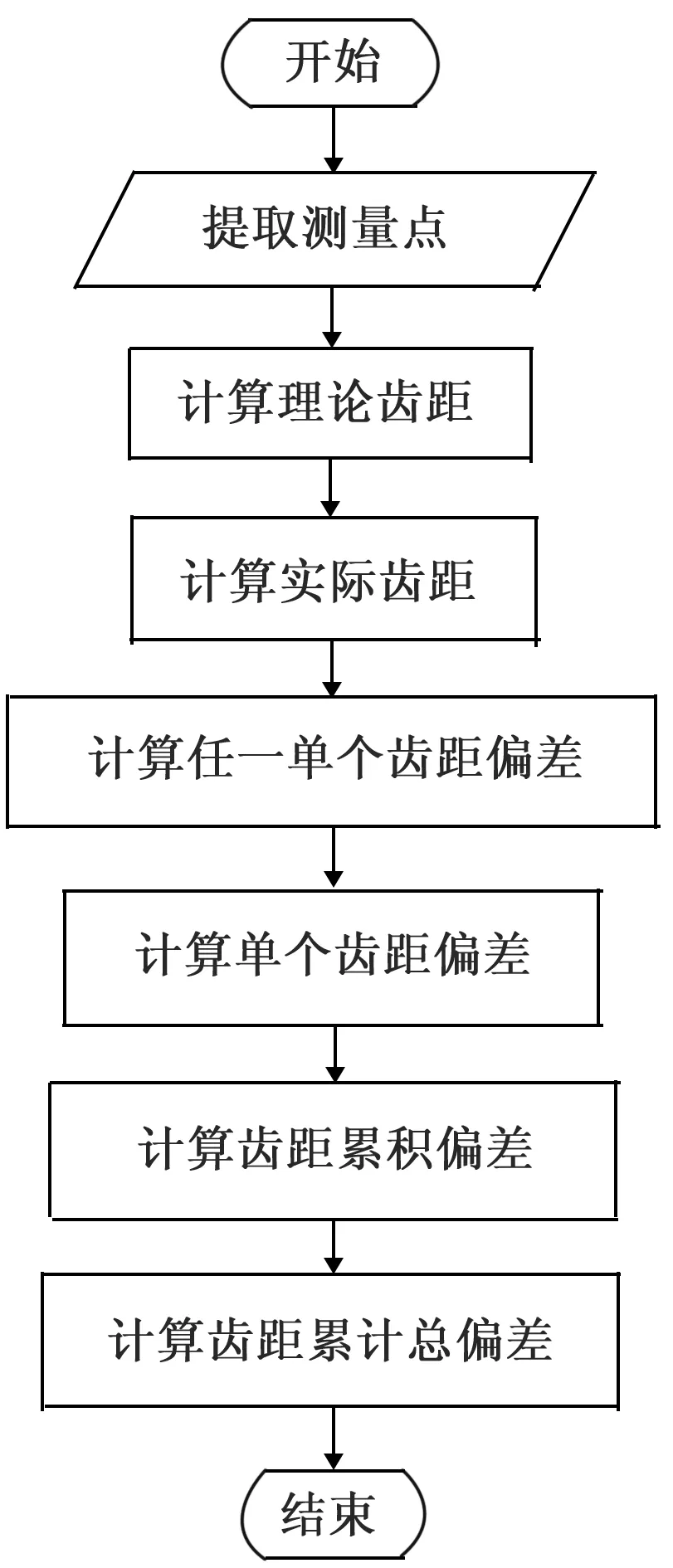
图7 齿距偏差求解流程图
在图像处理过程中,将齿轮轮廓与分度圆交点绕齿轮中心顺时针排序,并求出它们与x轴方向的角度,假设将排序的交点标记为P1、P2、P3…P2Z,交点相对于齿轮中心与x轴方向角度为θ1、θ2、θ3…θ2Z。
理论齿距为:
p=πm
(11)
第i个齿距为:
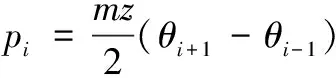
(12)
其中:角度的差值需要进行处理,使其在0到2π之间。
第i齿距偏差为:
fpi=pi-p
(13)
单个齿距偏差为:
fpt=max|fpi|
(14)
k个齿轮累积偏差为:
(15)
根据齿轮精度标准GB10095-88,齿轮累积偏差的k值规定取小于z/8或z/6的最大整数。
齿距累积总偏差为:
(16)
Fp=max(Fpk)-min(Fpk)
(17)
3 实验系统与测量结果分析
为了验证基于机器视觉齿测量轮齿距偏差的方法,搭建了影像测量系统平台,并进行了软件界面的设计,最后对测量结果进行了分析,验证了系统的重复性。本系统标定的像素当量结果为0.005 04 mm/pix。
3.1 实验系统图及参数介绍
本文中的齿距偏差影像测量系统搭建如图8所示。将它与opencv图像处理算法结合起来,能够精确的完成齿轮偏差的测量。

图8 齿距偏差影像测量系统
它主要包含型号VMS14M33COMS高分辨率工业相机,相机传感器光学尺寸为1/2.33 in,最高分辨率为4 320*2 430,像元尺寸1.43 μm*1.43 μm;型号CW-FM1614-8MP的定焦镜头,镜头焦距为16 mm,视场角(FOV)为21.8°*16.8°,畸变为0.05%,分辨率为10 Mega Pixel;此外,该系统还配备了LED光源、载物台、可升降支架以及上位机。系统通过工业相机采集齿轮和由于标定的棋盘格的图像信息,然后将图像传输到上位机中,由上位机中的程序完成图像预处理、提取测量点以及齿轮几何参数测量的功能。
3.2 操作软件界面设计
为了便于使用,使用pyqt5工具包进行页面设计,如图9所示为本次测试实验所做的操作软件界面,该界面可以实现图像采集、图像处理、系统标定、齿轮测量等功能,操作十分简单便捷。

图9 操作界面
3.3 齿轮齿距偏差测量
用工业相机从不同方位对待测齿轮拍摄多次得到多个图像,对每幅图进行图像处理,然后分别检测齿轮偏差,比较分析检测的结果。图像处理过程中,求得的齿轮的轮廓如图10所示,为计算方便,将其拆分成外轮廓和内轮廓。图11是构造分度圆过程中,得到的凸包图、齿顶圆和齿根圆与齿轮轮廓的交点位置。
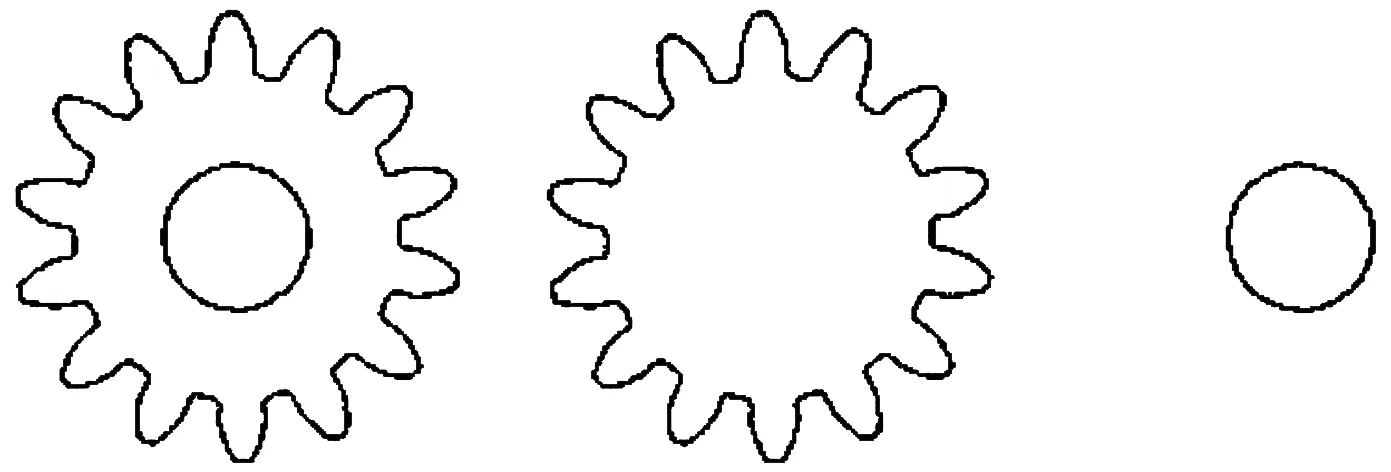
图10 齿轮轮廓示例图

图11 凸包结构、齿顶圆、齿根圆点集示例图
经过图10、11所示的齿轮轮廓、特征点提取等过程,得出本文所用待测齿轮齿数为14、模数为0.6,所以齿轮分度圆半径为4.2 mm。结果均符合实际。
对待测齿轮进行了测量,可以得到如表1所示的测量结果,每个待测齿轮14个齿距分别是以左齿面和右齿面为基准情况下的齿距偏差,测得的最大齿距偏差分别为35.055 μm和39.830 μm,可以得出,以不同齿面为基准测得的结果相一致。
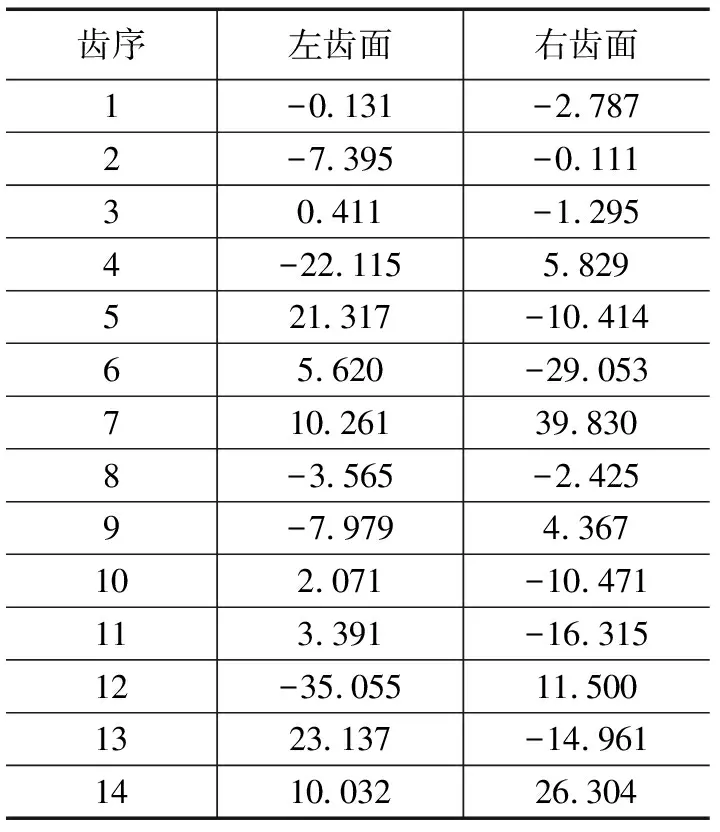
表1 任意单个齿轮偏差测量结果 μm
以1号齿轮为例,作出图12、13所示的梯形图,图中中横坐标1表示、齿序为1的齿距偏差、横坐标x表示齿序1至x的累积偏差。分别以齿轮左、右齿面基准测得的齿面累积总偏差为7.967-(-33.17)=41.137 μm和3.941-(-37.83)=41.771 μm,所以以齿轮左、右齿面基准测得的齿面累积总偏差也相一致。
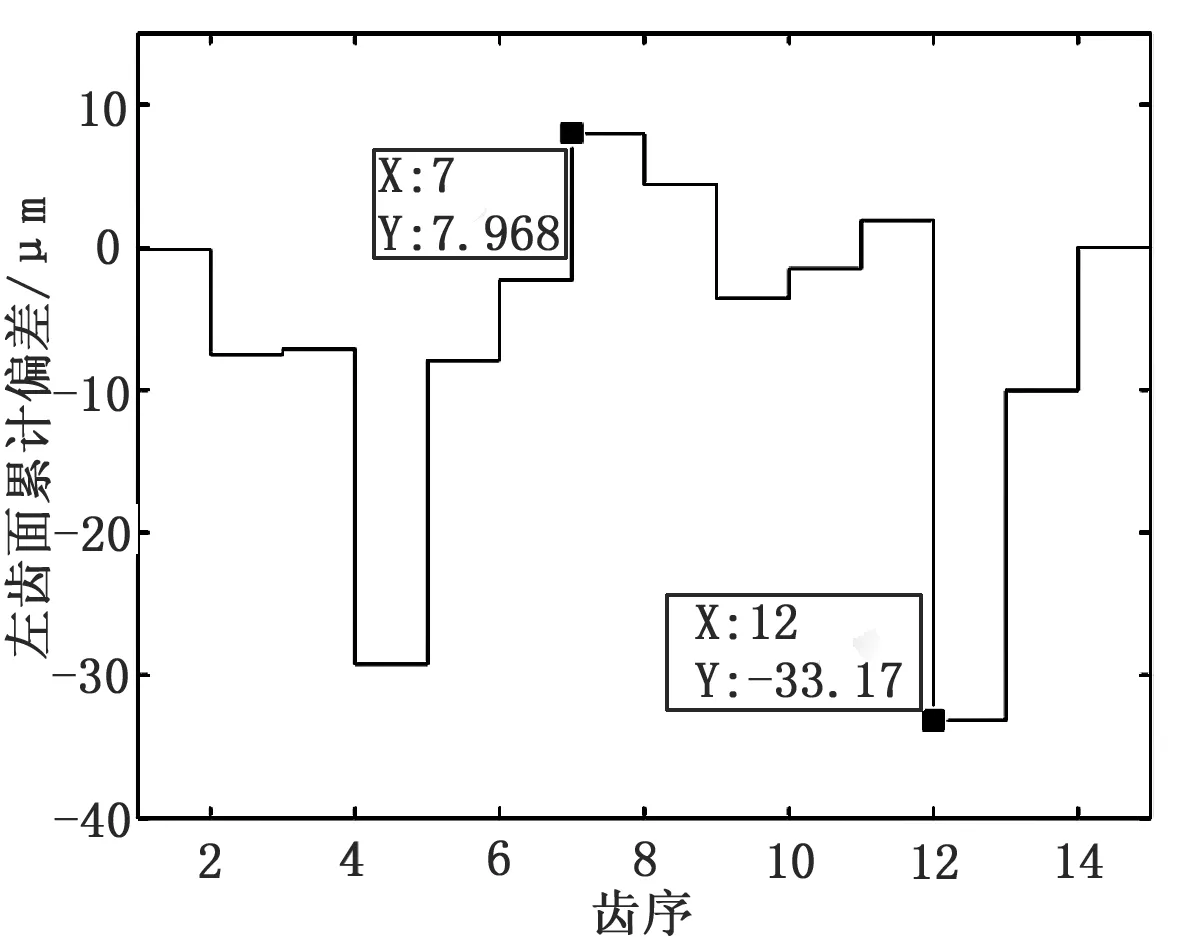
图12 以左齿面为基准齿距累积偏差

图13 以右齿面为基准齿距累积偏差
为了对测量结果的重复性进行分析,对同一齿轮测量了10次齿距偏差,其中,由公式(15)及其相关定义,求解齿距累积偏差时取k=2。如表2所示,对齿序1的齿距进行单个齿距偏差的重复性测试;同时又进行了以齿序1、2做齿距累积偏差和齿距累积总偏差重复性实验。使用贝塞尔公式如式(18)进行标准差的计算,来判断实验的重复性。
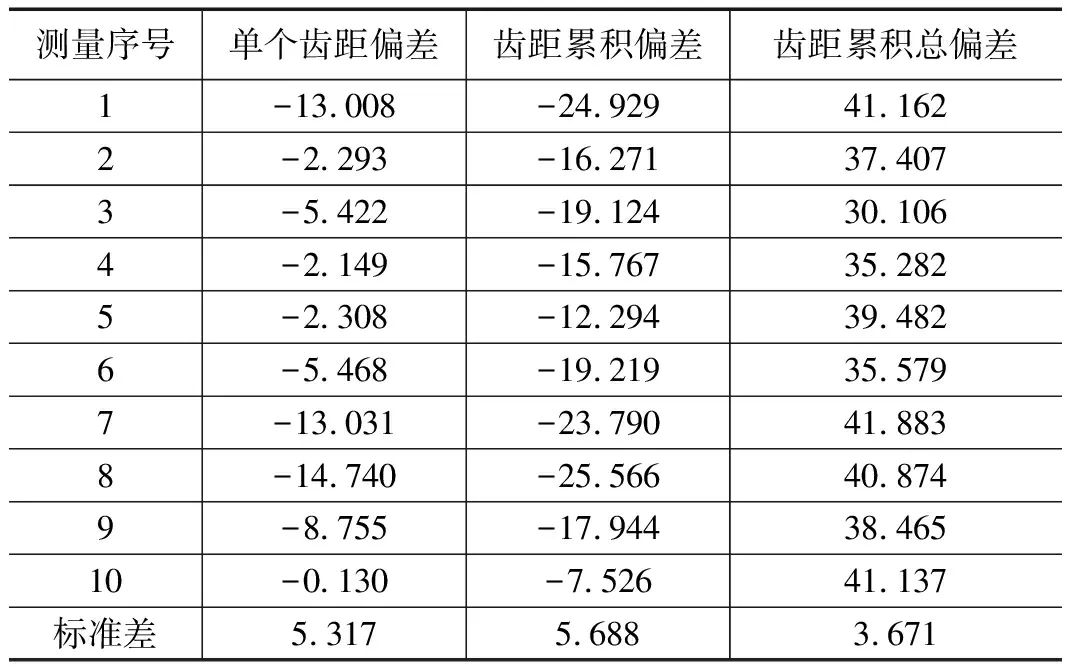
表2 待测齿轮重复性测量 μm
(18)
式中,n为样本个数。
由表2可知,对待测齿轮的的单个齿距偏差、齿距累积偏差、齿距累积总偏差的10次测量结果进行重复性分析,得到的重复性标准差分别5.317 μm、5.688 μm和3.671 μm。说明对该齿轮的测量满足重复性要求。
为了更好的验证本文实验系统的重复性精度,共准备了3组齿轮(每组有10个型号相同的齿轮)进行更进一步的重复性测量。由于齿距累积总偏差对齿轮运动精度的影响最大,所以对每个齿轮选用齿距累积总偏差测量10次来计算标准差。由图14可知,3组重复性测试的标准差最大值分别为5.014 μm、5.314 μm、5.302 μm,所以本文建立的影像测量系统可以实现对圆柱直齿轮齿距偏差的有效测量。
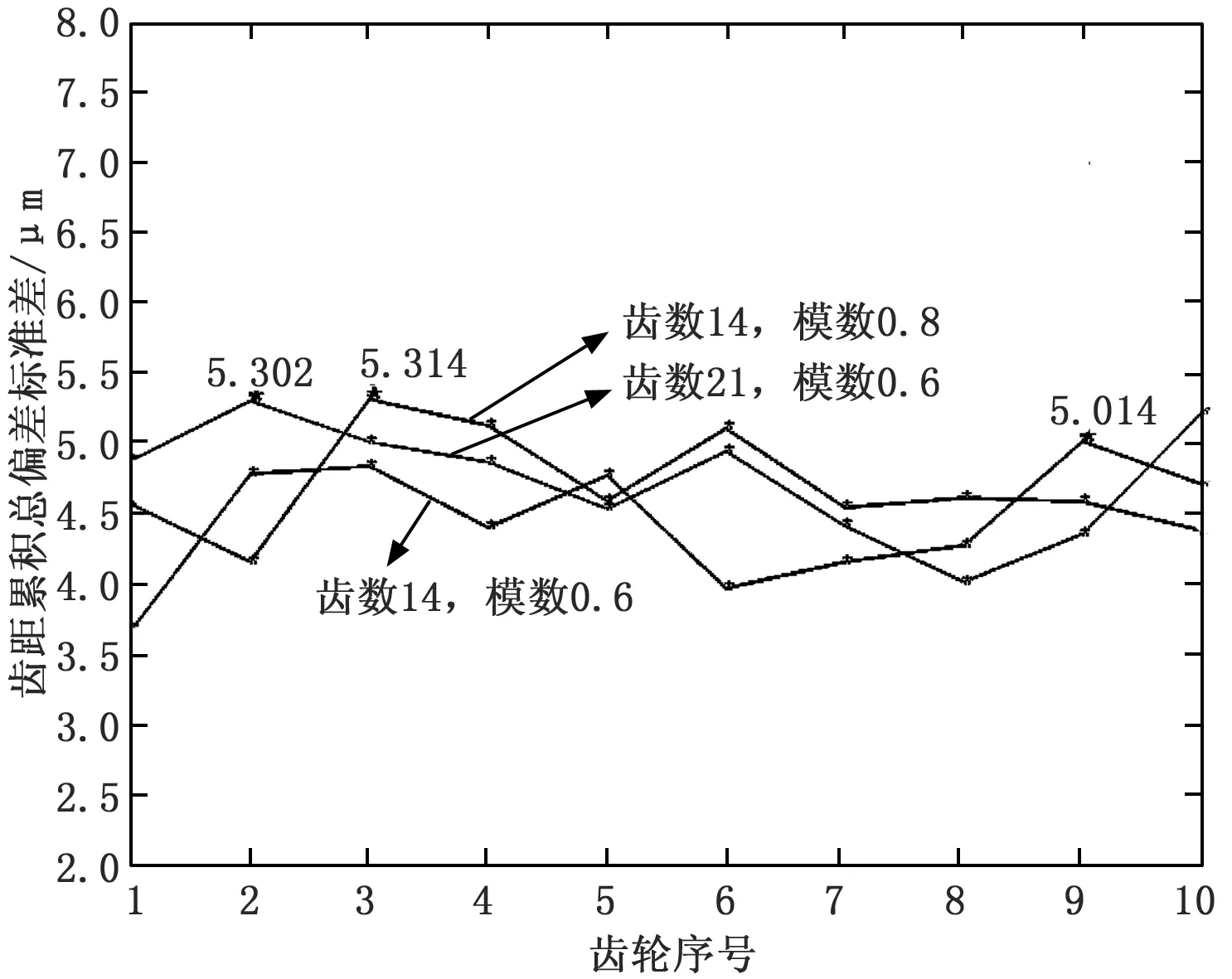
图14 重复性测试图
4 结束语
本文基于机器视觉技术对圆柱直齿轮齿距偏差进行检测方法研究。该方法利用影像测量系统摄取被测圆柱直齿轮端面图像,然后进行图像预处理、边缘检测、特征提取等算法处理图像,反求出齿轮的基本参数,如齿轮中心、齿轮齿数、模数等。通过齿距偏差的定义完成单个齿距偏差、齿轮累积偏差、齿轮累积总偏差的测量计算,与传统接触式测量或其它人工测量方法相比,基于机器视觉的圆柱直齿轮齿距偏差检测技术具有测量速度快、操作简单、自动化、对齿轮表面无损害,高精度等优点。
