基于差分进化的幕墙百叶伺服电机自抗扰控制

赵 蕾,白甲丽

(1.西安建筑科技大学 建筑设备科学与工程学院，西安 710055;2.西安建筑科技大学 信息与控制工程学院，西安 710055)

0 引言

伺服电机系统广泛应用于工业、农业、建筑业等等，例如对机械手、数控机床、幕墙百叶窗的调控。伺服电机系统常采用反馈控制系统调节。但是，气象条件存在不确定性，且建模时若考虑伺服系统摩擦对被控对象的影响就必须引入一些简化假设而使得模型结果并不能反映真实运行状况，以致传统的PID控制以及模糊控制等算法因计算过程简单而无法实现对扰动的补偿，难以达到控制精度的要求，而影响实际控制效果，如响应速度慢和精度不够等。

为了解决伺服电机控制中的这些问题，已经进行了大量研究[1-4]。韩京清在1998年首次提出了自抗扰控制(ADRC，active disturbance rejection control)，ADRC[5-6]，对输入信号安排了过渡过程，并跟踪过渡过程的微分信号，为扩张状态观测器(ESO，extended state observer)引入补偿因子，可提高系统的自抗扰性能。随后，自抗扰控制技术被应用于武器装备系统、飞行器以及发动机的控制中。

为了保证自抗扰控制系统稳态和动态性能良好，通过建立优化函数对自抗扰控制中的速度因子、滤波因子等参数进行了整定和优化研究，比如文献[7]提出了一种线性化、带宽化的线性扩张状态观测器，简化了扩张状态观测器算法。文献[8]以大时滞滤水浊度控制系统为对象，研究了参数整定后系统的控制性能。文献[9]引入中间变量提取参数估计误差来决定自适应控制率，使电机伺服系统对某惯性负载在有限时间内快速得到控制。文献[10]将改进的Smith预估器(MSP，modified smith predictor)与自抗扰控制结合，提出了MSP-ADRC算法，显著提高了一阶时滞系统的抗干扰性和鲁棒性能。文献[11]深入分析了自抗扰控制和免疫双态微粒算法，提出了一种具有创新性的免疫双态微粒群算法(BIPSO)，并与BP-PID、 PSO算法优化的ADRC、Fuzzy-RBF-PID这3种算法进行对比，通过仿真证明了BIPSO算法的先进性、可靠性，应用于混沌系统自抗扰控制器的参数整定。但这种新算法运算过程繁琐、复杂，所以不易推广与应用。扩张状态观测器存在状态估计误差的问题，为此基于自由度的内模控制被提出，且有效性得到了实验验证[12]。

自抗扰控制过程中的参数kp、kd对控制精度起着关键作用，而通常这两个参数取值由经验得到，大部分情况下需要手动调试得到尽可能满意的效果，但无法验证这样得到的参数是否达到最佳。文献[13]在1997年首次提出差分进化算法(DE，differential evolution)。随后学者们将差分进化算法与其PID、神经网络等算法相结合进行参数优化，使差分进化算法得到进一步发展。文献[14]利用差分进化的思想改进智能人工蜂群进化算法，加快了寻优收敛速度，同时提高了寻优精度。在处理不同的优化问题时，差分进化参数通常也不同，因此文献[15]对差分进化算法进行自适应动态调节，在伺服电机驱动光盘负载的控制中效果显著。

针对百叶对室内照度、温度以及建筑能耗的影响，大部分研究仅关注于百叶参数、百叶位置的设计[16-19]，对某一个时间段内百叶在外部干扰下的自动控制研究较少。本文采用自抗扰控制技术实现对带动百叶窗的伺服电机进行动态控制。为了使百叶角度随时间连续变化，对输入信号安排了过渡过程，引入扩张状态观测器来观测扰动并加以补偿，以提高系统的自抗扰性能。

在自抗扰控制的基础上引入差分进化思想进行参数寻优。对自抗扰控制的非线性跟踪部分的PD控制参数kp、kd进行动态优化，提出基于差分进化的自抗扰控制算法(DE-ADRC)，并将该算法应用于百叶窗伺服电机的自动控制中，与系统在PID、ADRC算法下的控制效果进行对比。

百叶伺服电机在DE-ADRC算法控制下实现扰动补偿的同时，可以相对准确地跟踪输入信号的过渡过程。进一步，为了验证所设计的DE-ADRC算法下系统的鲁棒性，本文利用蒙特卡罗分析法(Monte Carlo method)设计了系统性能指标，建立伺服系统概率模型。

1 伺服电机模型

伺服系统的电机和动力学方程如下所示。

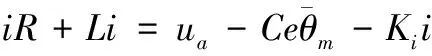
(1)

Tm=iKm

(2)

(3)

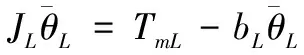
(4)

KL(θm-θL)-TmL=0

(5)

伺服系统运行进程中的摩擦过程较复杂，通常选用式(6)描述的LuGre摩擦模型：

(6)

式中，Fc为库伦摩擦，Fs为静摩擦，Vs为电机切换速度，α为黏性系数。

2 非线性自抗扰控制

典型非线性自抗扰控制器一般由微分跟踪器(N-LTD)、非线性误差补偿控制率(N-LPD)以及扩张状态观测器(N-LESO)三部分组成。自抗扰控制系统结构如图1所示。

图1 非线性自抗扰控制系统框图

2.1 非线性微分跟踪器(N-LTD)

非线性微分跟踪器可根据被控对象的状态和能力以离散形式给输入信号安排一个较为合理的过渡过程x1，并给出该过渡过程的微分信号x2，如式(7)所示，以使控制过程处于稳定调节状态。

(7)

其中：

(8)

(9)

式中，h为采样周期；v(k)为第k时刻的输入信号；r为决定跟踪快慢的参数，x1为v(k)的跟踪信号，x2为x1的导数，即x1的微分信号，h0为噪声滤波效应，为了使系统获得满意的性能，可以对δ和h0进行调整。

2.2 非线性扩张状态观测器(N-LESO)

扩张观测器是自抗扰控制的核心部分，用于观测外部干扰以使控制器提前进行扰动补偿。

对于如下控制对象：

(10)

该被控对象模型中，w(t)表示未知的干扰量，bu为已知部分。扩张状态观测器为：

(11)

一般情况下，α1、α2为固定值，β1、β2、β3均大于零，设α1=0.5；α2=0.2。为了抑制信号抖动需引入饱和函数fla(e,α2,δ)，可表示为式(12)。

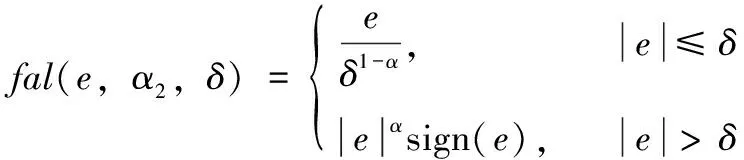
(12)

2.3 非线性误差补偿控制率(N-LPD)

非线性误差补偿控制率功能：将微分跟踪器得到的跟踪信号以及信号的微分与扩张观测器输出进行比较，进而对控制系统进行扰动补偿。数学表达式如下：

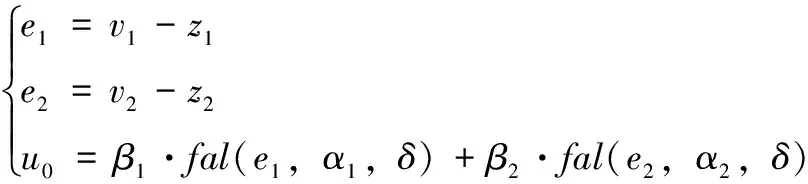
(13)

式中，0<α1<1<α2；β1=kp，β2=kd，e1为系统输入信号与系统实际输出之差；e2为输入信号的微分与被控系统实际输出的微分之差。

3 基于差分进化算法的自抗扰参数整定

在实际应用过程中，当确定选用PD控制时，不同的系统由于应用环境不同，其参数kp和kd也存在差异，要么为某一固定值，要么不断地人为手动改进，但却无法判断是否达到了最佳控制效果。所以需要对参数kp、kd寻优。由于参数kp、kd的变化对系统的整体响应性能之间存在着耦合关系，调节kp是为了加快系统的响应速度，而当kd过大时，超调增大，系统响应较慢，所以需要整定参数kp、kd，在保证响应速度快且同时需超调量小。

由于伺服电机具有非线性和强耦合性，而且控制百叶窗的伺服电机的控制受外部未知干扰因素较多，包括室外气象参数、建筑外围护结构热工性能、室内建筑设备运行状态等等。因此，为了获得较为满意的跟踪效果和动态特性，将误差的绝对值和时间积分性能作为最小代价函数。在代价函数中引入控制输入的平方项来避免发生控制过度，同时积分项引入权值参数w1、w2，如式(15)所示。

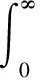
(14)

式(14)中，e(t)为动态系统误差；u(t)为控制输出。为了提高其工作效率，避免或尽量减少电机控制过程中的超调量，本文引入惩罚机制，将超调量的平方项作为指标项。对代价函数加以修改，如式(15)所示：

(15)

利用差分进化算法对参数kp、kd寻优步骤如下：

1)首先确定参数kp、kd的大致范围并随机选取M个个体；

2)将随机产生的M个个体作为初始化种群h(0)；

3)对h(0)中的个体进行解码，初始化差分进化参数，求代价函数J；

4)对种群个体进行编译、交叉、选择操作。若满足终止条件，则进行步骤5)，若不满足，继续执行步骤4)。

5)代价函数优化完毕，寻得最优解，进化结束。

基于差分进化算法的自抗扰控制原理如图2所示。

图2 基于差分进化的自抗扰控制原理的框图

参数kp、kd的整定由伺服电机的输出值和非线性控制率决定，能够在系统运行中实现动态优化，结合扩张状态观测器对扰动进行观测可以有效改善系统的控制性能。

工程中要根据实际情况来确定输入指令函数，而不是简单地采用常规的阶跃信号或正弦函数信号。本文研究的伺服电机用于百叶窗角度控制工程中，将对百叶窗角度的控制转化成对电机的角度控制。假设在西安典型夏季气象条件下，得到早上8:00到下午18:00角度指令信号，如图3，经过6次多项式曲线拟合得到几乎近似于输入指令的多项式函数如式(16)。

图3 输入信号及其拟合信号

yd= - 0.000 2t6+ 0.013 6t5- 0.178t4-

0.035 4t3+ 10.411t2- 35.089t+ 90.422

(16)

将式(16)作为实际指令信号输入控制系统。利用设计的DE-ADRC算法对电机角度实现随时间变化的连续控制。

4 仿真实验与结果分析

根据选用伺服电机的规格，它的参数设置如下：R=6.27Ω，Km=6 N·m/A，Ce=1.3 V(rad/s)，J=0.6 kg·m2。式(6)中的摩擦力的相关参数设置如下：α=0.03，Fc=0.31，Fs=0.36，Vs=0.01[20]。差分进化算法参数取值如下：变异因子F=0.5，交叉因子CR=0.9，种群规模取30，最大迭代次数取50。参数kp的取值范围是[0,20]，kd的取值范围是[0,1]，取w1=0.999，w2=0.9，w3=0.001。为了避免差分进化过程参数范围偏差过大，本文先根据经验，取kp=9.09,kd=0.08，假设在时刻12:00时天气骤变，有大风出现，相当于系统存在一定的扰动，参数整定前后系统的响应曲线如图4所示。

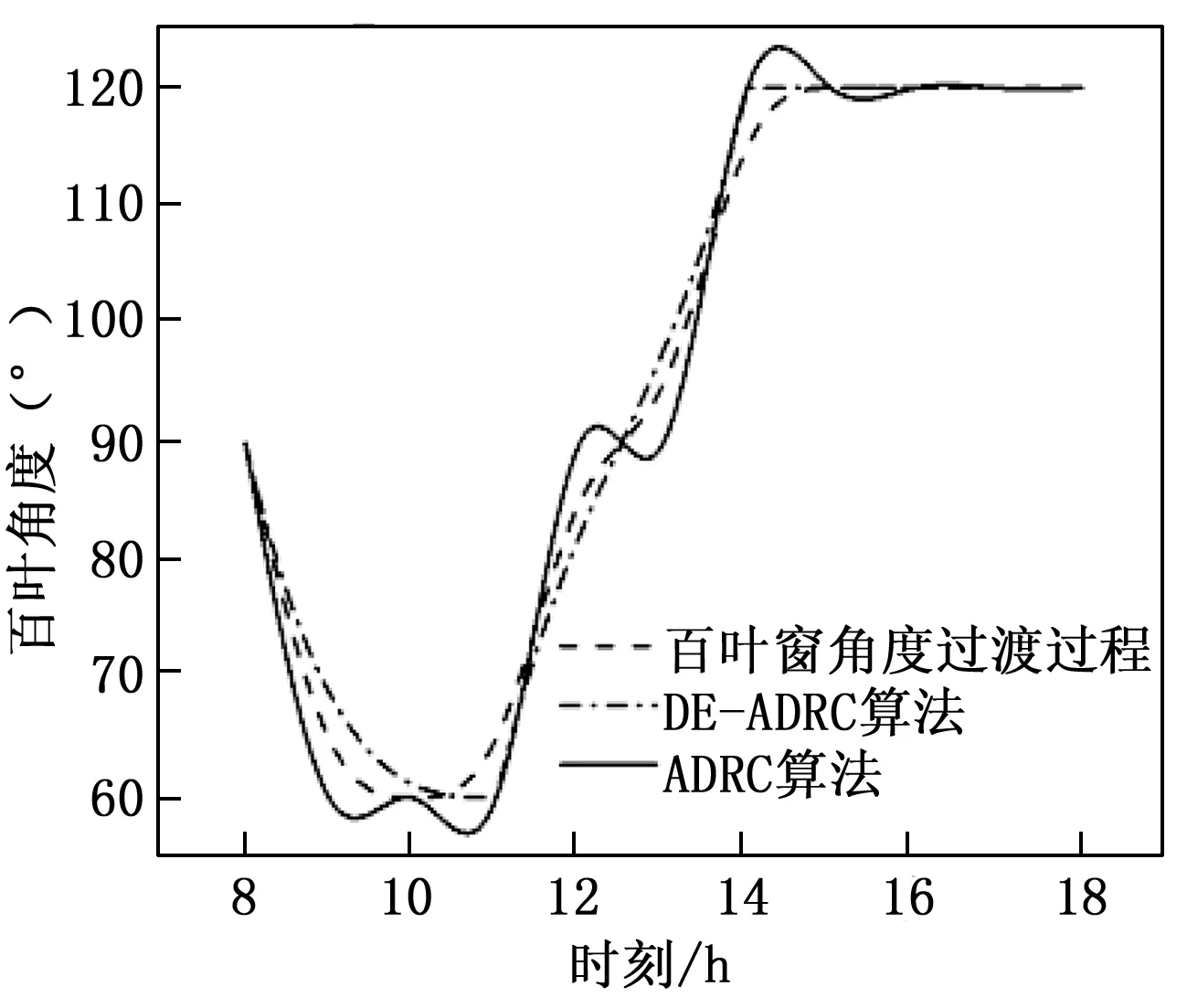
图4 参数整定前后系统响应曲线

图4表明当系统存在扰动时，经过差分进化对参数kp、kd整定后，其控制性能明显有所改善，跟踪误差显著降低，在DE-ADRC算法控制下，系统能较好地跟踪百叶角度的过渡过程，系统稳定性更加优异。经过50次迭代进化，最终整定结果为：kp=5.432 3，kd=0.089 6，代价函数整定结果为J=33.072 7，代价函数结果表示了50次迭代中实际值与设定值的误差和，kp、kd、J的整定过程如图5、图6所示。

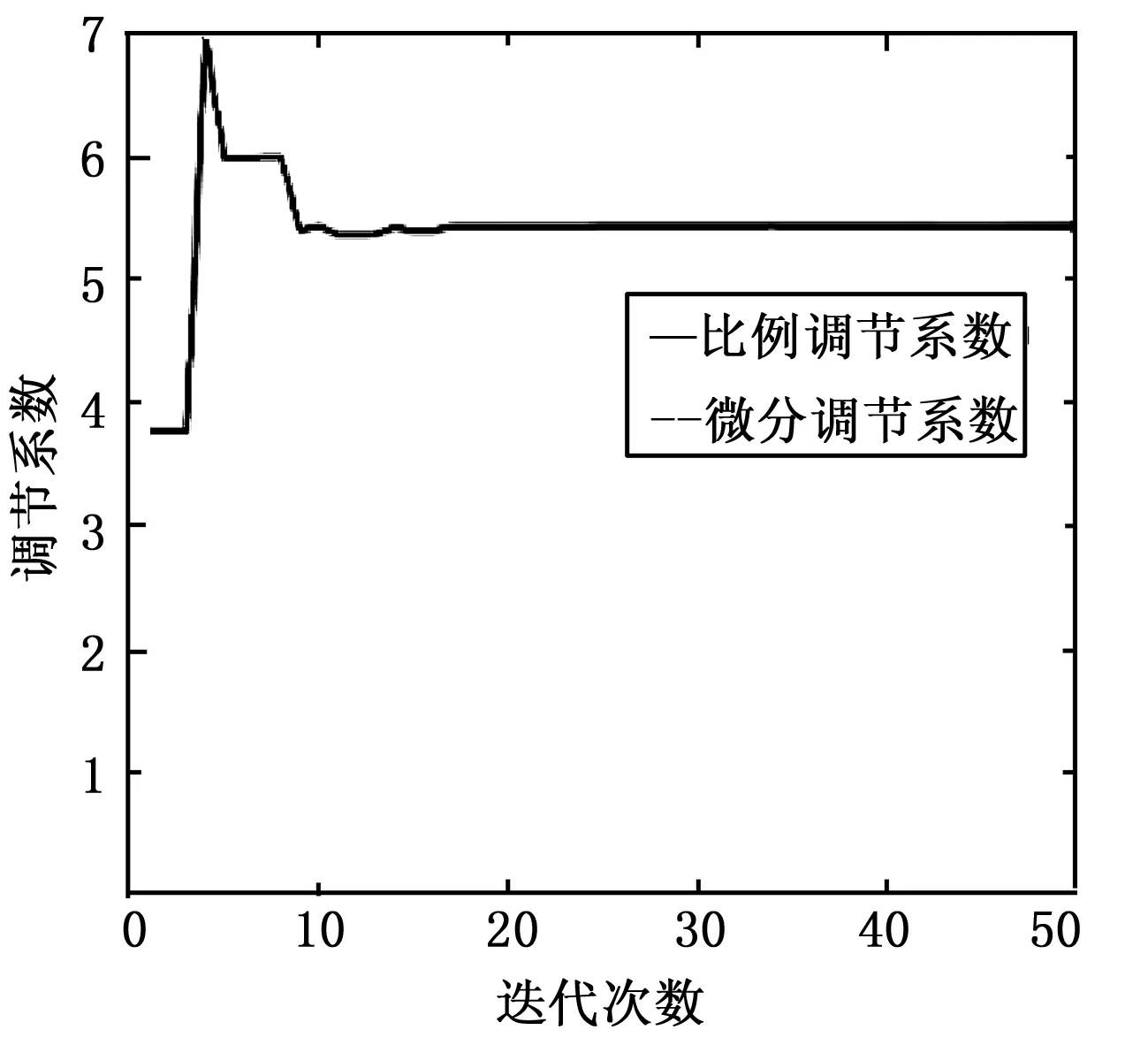
图6 代价函数J的优化过程

代价函数J、比例调节系数kp、微分调节系数kd的具体优化过程如表1。图5、图6表明在整个优化过程中，参数kp、kd和代价函数J的波动范围较小，迭代次数到15代时，优化基本结束。根据表1中的具体数据，当迭代次数达到48次时，代价函数J和微分调节系数kd不再发生变化，趋于稳定，当迭代到49次时，参数kp不再发生变化。

表1 优化代价函数J、比例和微分调节系数kp、微分调节系数kd的具体变化过程

为了探究控制算法的控制性能，分析后得到了PID算法、ADRC算法、DE-ADRC算法在1 s内的跟踪误差，对比如图7。从误差变化趋势可以看出，在响应时间达到0.5 s时，3种算法均能使系统误差得到有效控制，逐步趋于稳定。3种算法的平均误差分别为0.39°、0.27°和0.18°，均方根误差分别为0.84°、0.60°和0.38°。经过差分进化对参数进行整定后，系统响应幅度变小，能够更快地趋于零。DE-ADRC算法较PID算法、ADRC算法跟踪误差平均值分别降低了54%和49%。跟踪误差降低明显，证明了DE-ADRC算法对ADRC算法的参数整定效果起到了积极作用，提升了算法的控制性能，验证了所设计算法的可行性。

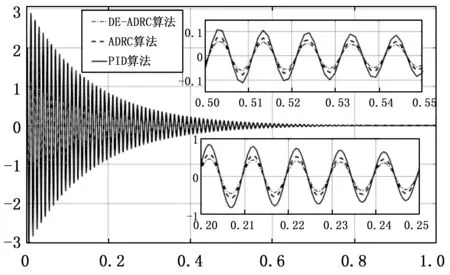
图7 PID、ADRC以及DE-ADRC算法的跟踪误差

5 系统鲁棒性的蒙特卡罗法分析

控制系统设计的最基本要求就是鲁棒性应较强。鲁棒性反映了被控对象在外界环境干扰下保持自身稳定性和可靠性的能力，鲁棒性越强，系统就越稳定，它决定着该控制系统的实际应用效果[21-22]。蒙特卡罗分析方法是以大数定律作为基础，通过对研究对象的随机采样进行统计学模拟的方法，可准确模拟存在不确定因素的实际系统的指标状态，算法简单，计算速度快，可用于系统鲁棒性分析，被广泛应用在金融学、系统工程学、信息科学领域[23-24]。本文将建立伺服电机系统的蒙特卡罗模型，通过求解来分析指标状态分布，揭示系统鲁棒性。

5.1 伺服电机的蒙特卡罗概率模型及求解

设置伺服电机系统的调节时间T、超调量E以及误差属性指标IAE等3个估计量。IAE定义如式(17)：

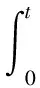
(17)

仿真时，对这3个指标变量进行随机抽样，当样本数N趋近于∞时，得到估计量的数学期望值，分别如式(18)～(20)：

(18)

(19)

(20)

2)随后对得到的3个期望值进行收敛，由于外部干扰的存在，收敛过程中可能出现偏差ε，由误差系数ηα和方差σ求得，如下所示：

(21)

以调节时间T为例，求解得到调节时间的状态分布如下：

p=(TK|Z1:K)

(22)

当样本数据T足够大时，状态分布无限接近实际样本分布。同理，超调量、误差性能指标的状态分布为:

p=(EK|Z1:K)

(23)

p=(IAEK|Z1:K)

(24)

5.2 不确定因素分析

为了验证本文提出的DE-ADRC算法的鲁棒性与稳定性，并与PID、ADRC两种算法进行对比，首先需要明确影响伺服电机系统运行的不确定干扰因素，才能更加真实地模拟出系统的概率模型。

本文以式(10)为研究对象，将控制百叶窗的伺服电机系统的不确定因素总结为以下几点：

1)室外天气状况的实时变化，尤其是当天气骤变时，若仍然采取先前确定的控制律则显然就达不到预期的控制效果；

2)伺服电机老化会逐渐加剧，而反映真实的情况的摩擦模型却难以建立；

3)室内人员的流动率以及设备的使用情况均会不同程度地影响室内温度，为改善室内热环境需要根据实际情况随时调整电机的控制律来调节百叶角度。

4)电源电压的不稳定性会影响伺服电机与负载的正常运行。

5)无法获悉因电机内部材料不同而在其运行时发热所对自身产生的不利影响。

5.3 蒙特卡罗系统鲁棒性仿真

这些不确定因素将被考虑到蒙特卡罗模拟中。经过400次蒙特卡罗算法进行仿真后，其结果如图8(a)～(c)所示。一般，若调节时间、超调量、误差属性指标的数值越小，则系统的控制效果越优秀，图中点越密集，说明控制算法鲁棒性和抗干扰能力越强，控制效果就更好。

由图8(a)～(c)可见，DE-ADRC算法结果的聚集性最强，超调量、调节时间和IAE三个指标数值最小，ADRC算法次之，PID算法的聚集性最差、指标值最大。这说明伺服系统在DE-ADRC算法控制下受干扰影响最小，系统的稳定性最强。也就是说，本文提出的DE-ADRC算法在鲁棒性和系统动态响应方面有着明显的优势，能更好的控制百叶窗。

图8 蒙特卡罗分析结果

6 结束语

本文针对玻璃幕墙百叶角度控制中伺服电机的准确模型并不完全已知，且可能存在气象条件变化等不确定外部干扰影响，提出一种基于差分进化算法的伺服电机自抗扰控制系统，研究对象为二质量伺服电机系统，通过引入摩擦模型，对自抗扰控制器的PD控制部分进行参数的动态优化，相比较于PID算法、ADRC算法，参数整定后系统的信号跟踪误差降低了54%和49%，证明了DE-ADRC算法的可靠性。

为了验证优化后系统的控制性能，对伺服系统设置了3个性能指标，采用蒙特卡罗算法对伺服控制系统进行鲁棒性仿真，总结了不确定干扰因素，并将其考虑到仿真模型中，分析得到本文提出的DE-ADRC算法的3个蒙特卡罗指标整体低于，PID算法、ADRC算法，鲁棒性和系统抗干扰能力更强。

综上，控制器的设计对系统性能影响较大，应根据系统所在的实际运行环境，尽可能全面地考虑一些不确定因素来设计符合情况的控制器，本文提出的DE-ADRC算法对自抗扰控制技术在幕墙百叶控制工程中具有实际意义。