聚类分析在消除轮轨力信号基线漂移中的应用
2021-12-01农汉彪曾巧妮
农汉彪,曾巧妮
(百色学院,广西 百色 533000)
0 引言
轮轨相互作用力监测是轨道交通车辆运行安全状态中非常重要的方法和途径。通过轮轨力的监测可以实时了解车辆运行过程中的减载率,脱轨系数等。在基于地面的轮轨力检测中,通常通过测量钢轨的动态响应来测量车轮通过时的轮轨相互作用力[1]。而在现场实测时,由于钢轨支撑条件会存在一定的不确定性,比如悬枕,扣件松弛,以及地基弹性突变等情况,使得轮轨力测试信号中会出现基线漂移的干扰[2],基线漂移的出现影响了后续的轮轨力信号的定量分析以及对列车运行状态的安全评估,所以必须予以去除。
去除基线漂移方法在心电图信号处理[3-4],脉搏信号处理[5],眼电图处理[6]等生物医学领域中广泛应用,在光学测试[7]和地震监测[8]中也有了相关的文献论述。而针对轮轨力信号降噪和基线漂移的消除,目前国内外较少涉及。
文献[9]中提出了基于分段数据中值聚类的算法,该算法将信号数据分成很多分段,取分段数据的中值,将中值的时间间距与幅值间距作为距离测度进行最近距离聚类,得到了能代表基线漂移的基点,拟合基点得到基线漂移干扰。算法效果良好,然而算法中需要设置不同测度之间的协调因子,且该因子的设置与数据长度,采样频率,数据幅值等因数相关。文献[10]利用LabVIEW提供的高级信号处理工具包和数字滤波器设计工具包对实测轮轨力应变信号进行处理,内容包括消除基准漂移、去除宽带噪声和提取信号特征等。文献[11]提出一种小波包降噪算法与经验模态分解(EMD)相关算法相结合的数据处理方法,有效地消除轮轨力在采集过程中随机白噪声的干扰和抑制模态的混叠。文献[12]提出了基于集合经验模态分解(EEMD)与小波变换相结合的去噪方法。对含有基线漂移的分量通过小波变换进行分解,将代表基线漂移的趋势项置零达到去除基线漂移的目的。
近年来,基线漂移的去除方法趋向于将原信号通过不同的算法分解成纯净信号部分和干扰成分,主要算法有基EMD及其改进算法,如EEMD[13], CEEMDAN[14]等,有经验小波分解(EWT)[15],傅里叶分解[16],变分模态分解(VMD)[17]等,而信号的分解总会存在频率混叠问题,传统的方法有FIR或IIR的方法,中值滤波[18],曲线拟合[19]和数学形态学滤波[20]等。曲线拟合方法是将信号中能代表基线漂移走势的基点拟合成曲线并从原始信号中除去。该方法高效、准确,计算量小,但是从原始信号中提取和确定基点比较困难。本文根据轮轨力信号短时分段数据的高阶统计量分布和基线漂移的关系,提出了基于分段数据高阶统计量聚类分析的方法获取基点所在的数据分段,以数据分段中值作为基点,再拟合即可得到基线漂移。
1 算法思想与实现
钢轨的模型通常采用连续弹性基础梁进行表示,钢轨垂直位移与移动载荷的大小,速度,位置之间关系表示为[21]:
(1)
其中:EI为钢轨的抗弯刚度,k为地基的弹性系数,m为单位长度钢轨质量,P为钢轨上载荷的大小,x为载荷作用点与观测点之间的距离,v为载荷移动的速度,δ(·)为狄拉克函数。
静态或准静态时,在多个载荷的同时作用下,钢轨上某观测点的剪力为:
(2)

在实测信号中,测试系统采集到信号除了钢轨载荷引起的响应之外,还包含了基线漂移成分和其他的随机干扰,即采集到的信号f(t)可以表示为:
f(t)=Q(t)+BW(t)+n(t)
(3)
其中:Q(t)为车轮载荷所引起的剪力测量值;BW(t)为基线漂移信号,n(t)为白噪声干扰信号,当所有|xi|>3πL/2时,Q(t)降为峰值的1%以内,此时BW(t)+n(t)Q(t),称无载荷区间即:
f(t)≈BW(t)+n(t)
(4)
根据随机噪声的对称性和基线漂移信号的缓变性,当所有|xi|>3πL/2时,短时间段内测试信号的中值即可表示为基线漂移成分的幅值,称为基点。而当存在|xi|<3πL/2时,测量值f(t)包含钢轨对载荷的响应,其数据段的中值不能表示为基点。拟合所有基点即可达到信号的基线漂移成分。而前提是正确筛选出能被视为基点的数据段中值数据。
对于f(t),由于Q(t),BW(t),n(t)相互独立,则有f(t)的方差:
D(f(t))=D(Q(t)+BW(t)+n(t))=
D(Q(t))+D(BW(t))+D(n(t))
(5)
BW(t)为缓变信号,在短时间内BW(t)为可视为常数,即D(BW(t))=0,而白噪声的方差D(n(t))可视为常数C;从而有当所有|xi|>3πL/2时:
D(f(t))=0+0+C=C
(6)
而在|xi|<3πL/2时:
D(f(t))=D(Q(t))+0+C=D(Q(t))+C
(7)
另外,同样可以看到,在短时间内信号的峭度值:
(8)
其中μ为f(t)的数学期望,σ为f(t)的标准差,由于Q(t),BW(t),n(t)相互独立,有:
K(f(t))=K(Q(t))+K(BW(t))+K(n(t))
(9)
短时间内BW(t)是均匀分布,即K(BW(t))=0,n(t)为正态分布,K(n(t))=3;从而有当所有|xi|>3πL/2时:
K(f(t))=0+0+3=3
(10)
而在|xi|<3πL/2时:
K(f(t))=K(Q(t))+0+3=K(Q(t))+3
(11)
联合方差与峭度,无载荷期间内数据段的D(f(t)),和K(f(t))将主要分布在以方差和峭度为坐标轴的点(0,3)和点(C,3)附近,而承载期间的坐标位置将远离这两点坐标。根据以上分析,可以通过对分段数据的方差和峭度进行基于密度的聚类分析来筛选出无载荷期间的数据段。
基于密度的聚类分析可以将具有相同或相近特征的对象样本之间的分为同一类,即在某类别任意样本周围一定空间范围内一定有同类别的样本存在,能有效区分有载荷期间数据段和无载荷期间数据段。基于密度的聚类分析的常用算法有DBSCAN,OPTICS和DENCLUE等。DBSCAN需要设定点数阈值minPts和邻域半径,全局密度,DENCLUE需要设定密度阀值和参数,这两种算法的效果对参数非常敏感,需要确定合适的参数才能得到理想的效果。OPTICS是DBSCAN的一种改进方案,也要设定点数阈值minPts和邻域半径,但聚类结果对参数不敏感。
基于以上分析,应用基于密度的聚类分析可以有效找到信号中基点,从而实现基线漂移的消除。该方法的具体过程和步骤如下:
1)对测量数据进行分段。前后数据段之间可以部分重叠,以加大数据段数量和保证数据的连续性;
2)计算每数据段方差和峭度值,并分别进行归一化处理;
3)针对归一化方差和峭度两个维度进行基于密度的聚类分析;
4)筛选出聚类结果中处于零点附近的一个分类或几个分类;
5)对选用分类所对应的数据段取中值,即为基点;
6)曲线拟合所有基点得到基线漂移干扰。
分段时,数据段的大小需要根据信号自身的成分来确定。涉及到信号数据的采样频率,通过列车的转向架间距,轴距和运行速度等。分块大小的最优设置是能将信号的负荷状态和非负荷状态完全分开,这是理想的情况,而实际上由于信号数据初始采集相位未知且列车运行速度并不恒定原因,无法在未识别压头时刻的情况下实现理想分段。而总会出现部分分段横跨负荷状态和非负荷状态两种状态的情况。根据数据试验结果一般采用的分大小可为:
(12)

分段数据的方差和峭度都是非负数值,但具有不同的数值范围,基于密度的聚类需要考虑数据点之间的距离测度或相似度测度,为了均衡方差和峭度在距离测度上的贡献,需要对方差和峭度进行归一化处理。归一化时可以将最大方差和最大峭度置为1,最小值置为零,其他进行线性化处理。
在聚类分析时,选用对参数不敏感的OPTICS算法,OPTICS所需要点数阈值minPts和邻域半径ε两个参数可以通过自适应的方式来确定。邻域半径ε可以取所有数据样点两两间距测度密度分布函数的最快下降梯度点所对应的距离测度,minPts可以取使得当前ε下所有分类间距总和最小的阈值。
2 仿真数据分析
为了定量分析基线消除方法的效果,预先准备一组零漂移轮轨垂直力信号和一组已知基线漂移信号。假设列车为两轴转向架,车辆定距为7.67 m,转向架轴距为1.75 m,车辆长度为11.986 m,列车低速经过观测点的车速为4 km/h,信号采样频率为1 000 Hz,数据长度为60 000点,各轮轨力信号峰值随机分布在1.4~1.7之间零漂移轮轨垂直力信号图1所示,数据本身具有很低的频率成分,该频率成分与列车转向架间距,轴距与列车速度都有关系。基线漂移信号为:
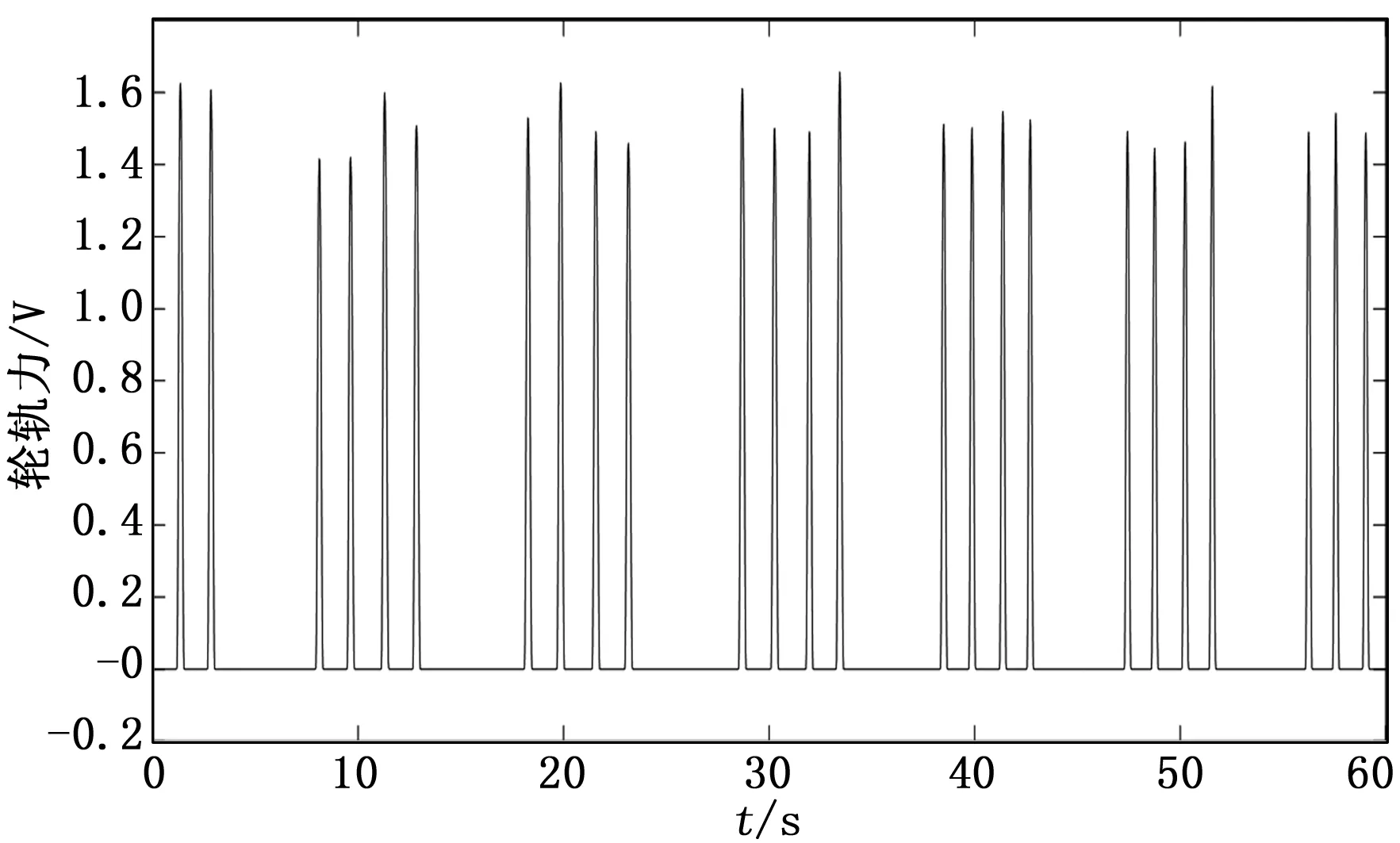
图1 零漂移钢轨垂直力信号
BW(t)=0.15*(sin(0.15πt)+sin(0.09πt+0.2π))
(14)
采用与力信号相同的采样间隔。基线及与力信号叠加后的结果如图2所示。

图2 基线及与力信号叠加的结果
常用于定量分析滤波算法性能评估参数主要有均方误差(MSE)和信噪比(SNR)等[22]。对于性能评价,MSE值越小越好,SNR越大越好。它们的定义分别为:
(15)
(16)

根据分段大小的分析,仿真数据可以采用分段大小为500数据点对含有基线漂移的信号数据进行分段,分段窗口步进长度为250。分段后的数据分段中值如图3所示,大部分分段数据的中值和已知的基线漂移重合,另一部分偏离较远。
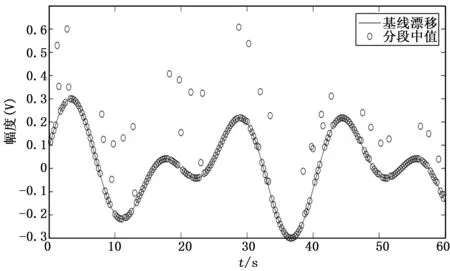
图3 含基线信号分段取中值的结果
随后对所有数据分段统计数据分段的方差和峭度,得到的方差和峭度数据如图4所示。
方差数值在0~1范围之内,而峭度数值在0~80范围之内,分别对方差和峭度进行线性归一化,然后对归一化后的数据进行聚类分析得到如图5的分类结果。

图5 聚类分析结果
图5中,数据点被分成了两个分类和部分未分类样点。根据轮轨力数据的特点,选用分类1作为无载荷期间的数据段。对分类1所对应的数据分段中值即为信号数据的基点。基点数据与目标基线漂移的位置关系如图6所示。

图6 选用基点与原始信号
为了对比分析,利用移动中值滤波,形态学滤波,(BEADS,baseline estimation and denoising with sparsity)[23],CEEMDAN,EWT,VMD,零相位滤波器以及本文提出的方法分别对图2中含有基线漂移的力信号进行处理。在这些方法可分为两类,一类是CEEMDAN,EWT,VMD和零相位滤波器,另一类是移动中值滤波,形态学滤波,BEADS和本文的方法。第一类主要是信号分解与重构的方法和数字滤波的方法,这些方法会将所有的测量数据值进行计算,这使得在有载荷期间的基线漂移的提取会受到载荷大小的影响。各种方法通过优化设置参数得到最优的结果如图7所示。所得结果与目标基线存在较大的误差,不适合后续的定量分析。

图7 第一类方法提取基线漂移结果
第二类方法中,设置移动中值滤波的移动窗口大小为700数据点,移动步进为一个数据点,然后再经过1 Hz低通滤波器得到最优的平滑基线;数学形态学滤波采用长度为350数据点的横条型结构分别进行开闭运算然后取两部分和的一半,再经过1 Hz低通滤波器得到最优的平滑基线;依据文献[23]BEADS方法采用截止频率为0.8 Hz,阶数为1,不对称参数为12,正则化参数为0.01。由于BEADS方法对任何信号提取的基线首尾均为零,需要先对原信号的首尾置零提取趋势线再进行提取,才能得到最佳的评估效果。不同方法提取的基线漂移与目标基线的误差如图8所示
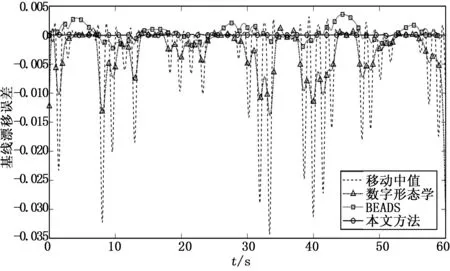
图8 提取的基线漂移与目标基线的误差曲线
从基线漂移误差曲线看到,移动中值滤波和形态学滤波具有形同的变化规律,即会在观测点负载时会有较大误差而其他时刻的误差趋于零,BEADS方法在信号的两头出现较大的误差,而中间部分误差较小。而本文的方法提取基线的误差相对其他3种方法都要小。原始带基线漂移的信号在经过不同方法去除基线前后的相似测度参数如表1所示。

表1 不同方法去除基线漂移的效果
从表1的数据结果表明,本文的方法对于仿真数据的消除基线漂移的两种评价指标均优于形态滤波等其他3种方法。本文方法的均方误差MSE仅约为次好的BEADS算法的0.47%,而信噪比SNR则高出23 dB。
3 实测数据分析
实测数据中,除了基线漂移的干扰之外还会有其他噪声的存在,如工频干扰和随机干扰等。如图9所示为一组数据现场实测轮轨力信号。

图9 实测轮轨力信号
依据算法,首先获取数据峰值宽度以确定数据分段的大小,接着对实测信号进行数据分段,统计分段数据的方差和峭度,基于方差和峭度统计数据段之间距离,按距离分布函数获取最优聚类领域半径,然后进行基于OPTICS算法进行聚类分析,得到聚类结果如图10所示,选用分类1所对应的数据段,以该分类数据段的中值作为基点,拟合所有基点得到基线漂移成分,如图11所示。

图10 实测信号分段数据高阶统计量聚类结果

图11 实测轮轨信号基线漂移的基点的选取
实测信号没有预知的基线漂移或纯净的信号数据,无法进行量化的评估。为了验证本文方法的效果,采用移动中值滤波,形态学滤波,BEADS方法分别对实测信号进行处理,对比的方法通过调整相应的参数使得处理结果达到最佳效果。图12为不同方法消除实测轮轨垂直力信号基线漂移的效果。其中最上方的曲线为实测的原始信号,往下分别为移动中值滤波加低通滤波的方法,形态学滤波加低通滤波的方法,BEADS方法以及本文方法去除基线漂移后的信号波形图。

图12 实测轮轨力信号基线漂移的消除效果比较
从图上看,本文的方法和BEADS方法于实测数据中的基线漂移的消除效果明显优于前两种方法。本文的方法和BEADS方法都能有效地去除基线漂移的干扰,仅从视觉上看,两者无法区分两者优劣情况。从计算量上,由于本文的方法采用分段的方法,使得整个计算过程的计算量相比与移动中值滤波、形态学滤波和BEADS方法大大的减小,提高了计算效率。
4 结束语
本文针对轮轨垂向力信号的基线漂移消除问题,提出了基于分段数据高阶统计量聚类分析的方法来确定信号基点所在的数据段,统计选用数据段中值作为基点,曲线拟合基点即可得到信号的基线漂移干扰。文中通过仿真数据和现场实测信号从定量和定性两种方式对所提出的方法进行了验证,并与现有常用的基线漂移去除方法进行了横向比较。验证结果都表明相比于其他方法,本文的方法在定量上具有更高的信噪比和更小的均方误差,在对实测信号的定性分析上同样具有很好的效果,而且计算量更小,速度更快。本文方法的参数设置可以根据信号的特性自适应设置,不需要过多的人为参与。该方法同样适用于其他包含有基线偏移的测试信号的处理,比如心电信号,光谱信号,脉搏信号等。
