基于谱聚类和L2,1范数的多视图聚类算法*
2021-12-01马盈仓续秋霞
贺 娜 马盈仓 张 丹 续秋霞
(西安工程大学理学院 西安 710600)
1 引言
聚类分析是把一个数据样本集划分为多个簇的过程,应用到许多领域,包括图像模式识别、商务智能和生物学等。通常来说,对于每个样本,可以对其从不同的视图进行描述,并且综合多个视图的信息有利于得到更好的聚类结果。处理这一问题的方法一般分为基于图的方法[1~3]、矩阵分解方法[4~6]、基于多重核的方法[7~9]和基于子空间学习的方法[10~11]。特别是基于图的方法,因其具有挖掘非线性结构信息的能力,在聚类精度方面通常优于其他方法。
经典的谱聚类算法是一种重要的基于图论的聚类算法[12],不仅可以在任意样本空间进行聚类,而且可以收敛到全局最优[13]。但是,该算法也存在一些问题,因谱聚类的最终结果完全依赖于开始构造的相似矩阵,然而不同的构造方法会影响聚类结果,因此构造理想的相似矩阵成为了一个问题[14]。
近年来,许多学者对谱聚类算法中相似矩阵的构造方法做了进一步研究与改进。Shi等通过高斯核函数构造相似矩阵[15];Ng等提出NJW(Ng-Jor⁃dan-Weiss)算法通过高斯核函数构造相似矩阵,采用全连接构造方法[16];Zhang等利用两个样本数据点之间的局部密度求得相似矩阵[17];Nie等通过基于局部连通性为每个数据点分配自适应和最优邻居来学习相似矩阵[18];Xie等采用样本点与样本点的近邻点两者的欧式距离作为局部标准差构造相似矩阵[19];Nataliani等利用数据点的相关性估计幂参数构造幂高斯核函数来求解相似矩阵[20]。然而这些文献中构造的相似矩阵都是固定的,不能很好地挖掘和利用数据结构。
为了更好地挖掘和利用数据,近年来发展起来的多视图学习,在学习过程中充分利用多视图数据之间的互补信息和关联信息,使最终的学习结果在各视图上趋于一致的机器学习算法。本文将多视图学习引入谱聚类过程,提出了基于谱聚类和L2,1范数的多视图聚类算法(Multi-view clustering algo⁃rithm based on spectral clustering andL2,1norm)。将改进的多视图亲和矩阵利用L2,1范数正则项合理地构造出相似矩阵S,同时进行谱聚类过程,F与S交替迭代更新,最后对F进行聚类。该算法不仅可以更好地反映数据的流行结构,而且可以得到更加稳定的聚类结果。
2 相关工作
2.1 多视图相似矩阵的构造
为了充分利用多视图数据之间的互补信息和关联信息,本文将不同视角下的亲和矩阵通过相加的方式,融合为一个全局亲和矩阵Â,即(v为视图的个数),由于学习的相似矩阵S与全局亲和矩阵Â存在距离,为了得到更好的结果,进一步对相似矩阵进行稀疏化处理,通过L2,1范数的鲁棒性学习得到一个最理想的相似矩阵S,表示如下:
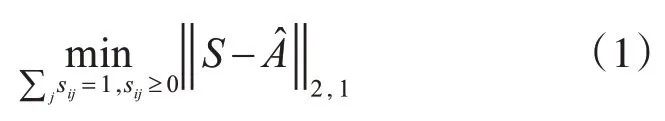
其中:我们限制相似矩阵S的每一行和等于1,使其具有仿射性,有利于后期的计算处理。
由于使用L2范数的平方作为损失函数对较大的异常值比较敏感,对较小的异常值不敏感;使用L1范数作为损失函数对较大的异常值不敏感,对较小的异常值比较敏感。然而L2,1范数[21]不仅综合了L2范数和L1范数的鲁棒性优点,还减少了异常值的影响,并保持了适当的稀疏性。
2.2 谱聚类中引入多视图学习的合理性
在2.1小节中,我们介绍了多视图相似矩阵的构造保留了各个视图携带的信息,在学习过程中充分利用多视图数据之间的互补信息和关联信息,使最终的学习结果在各视图上趋于一致,构造了一个合理的相似矩阵,本节为了说明在谱聚类中引入多视图学习的重要性,设计了如下实验。
我们将经典的单视图谱聚类算法(即将谱聚类算法在每个视图上分别执行)与2.1小节中构造的多视图相似矩阵的算法在数据集ALOI(具体介绍见4.1小节)上构造相似矩阵,参数k均为10,并通过影像图展示,如图1所示。所测试的多视图数据集ALOI有4个视图,即X={X(1),X(2),X(3),X(4)}∈Rn×dv,分 别 为X(1)∈R64×1079,X(2)∈R64×1079,X(3)∈R77×1079,X(4)∈R13×1079。
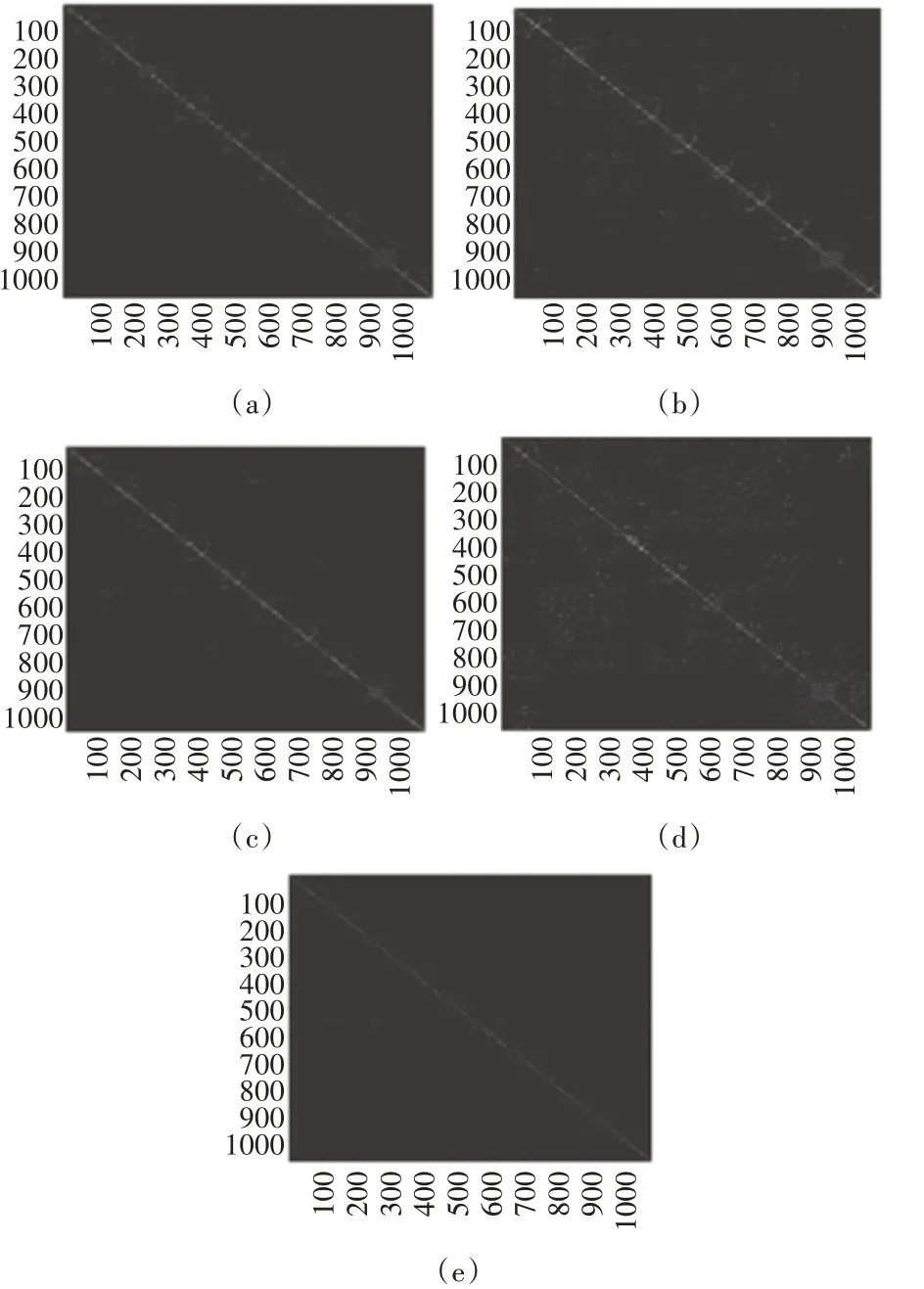
图1 ALOI数据集上生成的相似矩阵影像图
在图1(a)~(d)为在每个视图上分别执行谱聚类算法得出的相似矩阵影像图,图(a)为视图1相似矩阵影像图,(b)为视图2相似矩阵影像图,(c)为视图3相似矩阵影像图,(d)为视图4相似矩阵影像图,(e)为2.1小节构造的多视图相似矩阵生成算法得出的相似矩阵影像图。我们可以看到,经典的单视图谱聚类算法在视图1和视图2的时候,还可以构造出较为合理的相似矩阵,但是在视图3和视图4时,结果很不理想,特别是对视图4构造相似矩阵时,表现出很不好的结果。而相比经典的单视图谱聚类算法,图(e)可以很明显地看到,多视图学习方法可以构造出比图(a)~(d)更合理的相似矩阵,比单视图谱聚类算法更加稳定。
由此可以得出,在谱聚类算法中引入多视图学习方法,可以构造出更合理的相似矩阵,证明了多视图学习的优越性和有效性,有利于提高聚类精度。
3 模型的建立及求解
3.1 模型建立
在2.1小节中,构造了理想的相似矩阵,接着,在谱聚类的过程中引入多视图学习,同时进行相似矩阵的学习和谱聚类过程,建立目标函数为
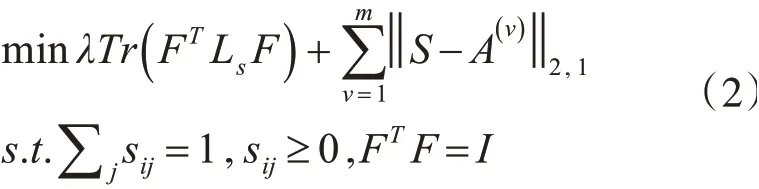
3.2 模型求解
对于上述目标函数式(2),我们通过迭代交替优化方法来求解。
1)固定S,问题(2)可以转化为
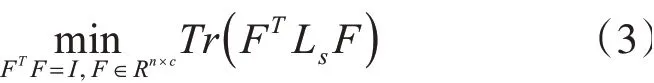
最优解F由Ls前c个最小的特征值所对应的c个特征向量构成。
2)固定F,对于式(2),根据文献[22],已知存在fi∈Rc×1,则下式成立:

由于式(2)对于不同i是独立的,因此我们可以分别对每个i求解如下问题:
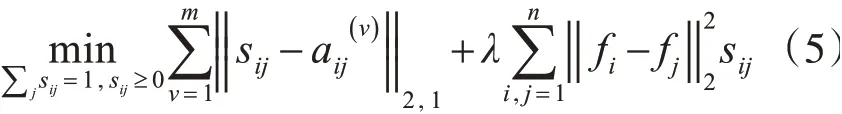
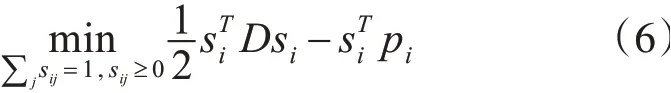
其中:D为对角矩阵,主对角元素dii=1/
根据拉格朗日乘子法,得
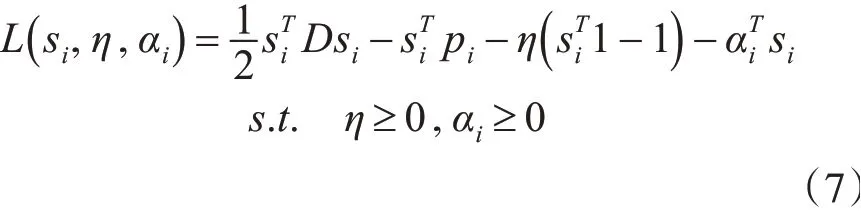
对si求偏导,令其等于0,可得
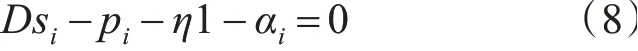
对si的第j个元素,有
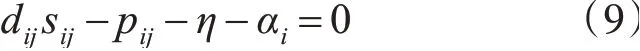
根据KKT条件,得
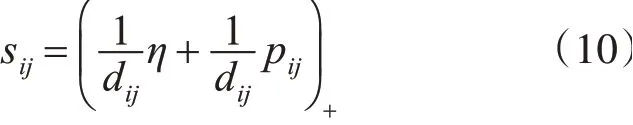
其中(v)+=max(0,v),定义η下述函数为
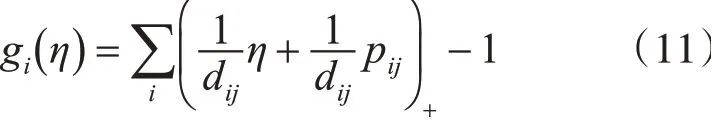

注意上式,gi(η)是一个分段单调递增函数,可以很容易地用牛顿迭代法求解。
3.3 算法流程
MVSC-L2,1算法流程如下所示。

3.4 收敛性证明
引理1[21]对于任意非零向量x,y∈Rc,有以下不等式成立
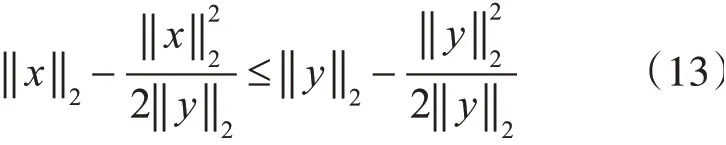
联合本文的目标函数,给出如下定理:
定理1目标函数
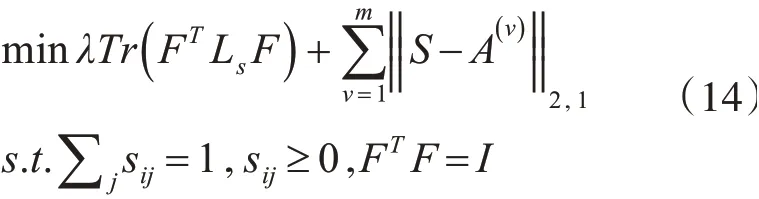
在固定F时,交替迭代优化S的过程中,目标函数值逐步减小。
证明:令更新后的si为sdow i,上一次的si为,通过式(5)只是式(6)的一个解,而是式(2)的最小解,所以根据式(2)有
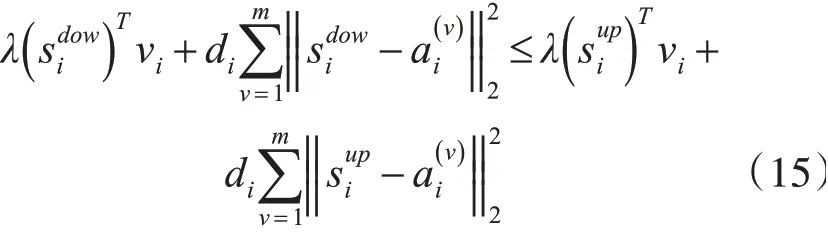
因为
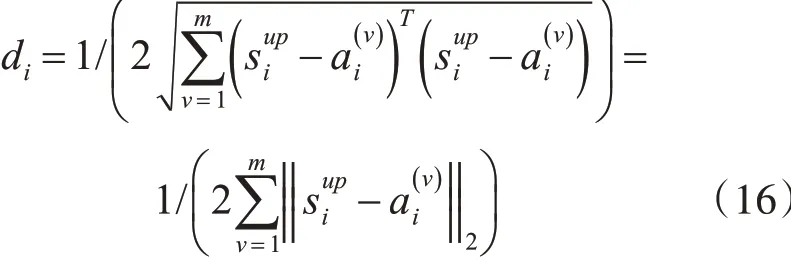
所以
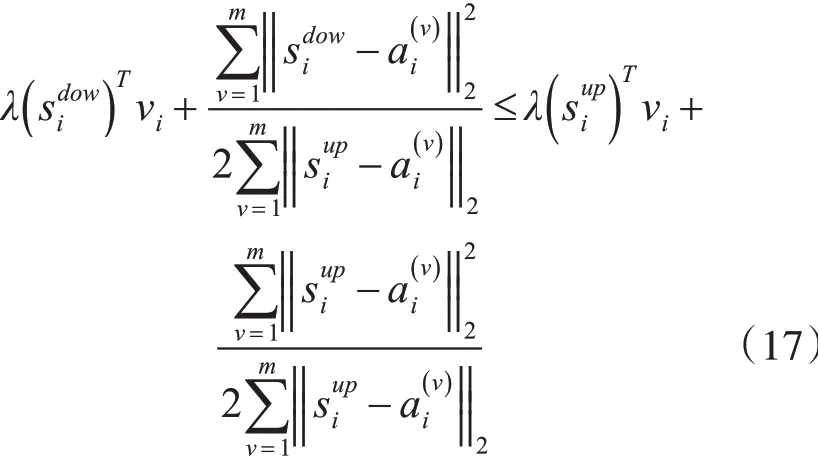
由引理1知道:
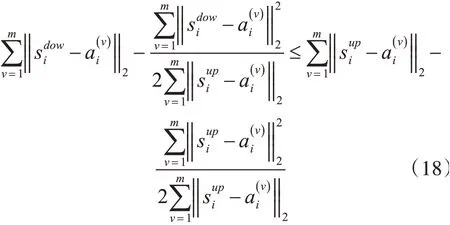
将式(17)和式(18)相加得
由L2,1范数[21]的定义可得:
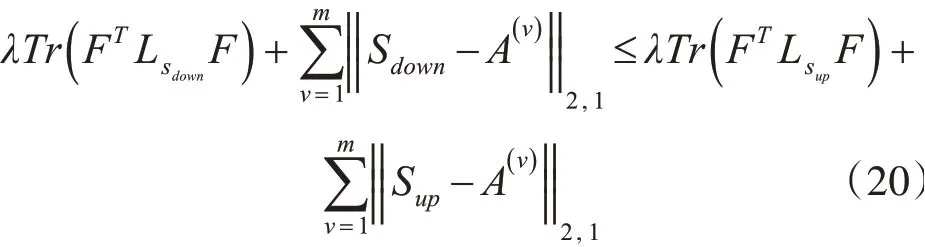
因此该算法收敛。
4 实验
在这一节,将根据三个评价指标[23]来评估我们的结果:聚类精度(ACC),纯度(purity),标准化互信息(NMI),对MVSC-L2,1进行评价。
4.1 数据集
3-Sources[24]该数据集包含294篇新闻文章,涵盖六个标签:商业、娱乐、健康、政治、体育和技术。第一视图有3068个特征,第二视图有3631个特征,第三视图有3560个特征(http://mlg.ucd.ie/datasets/3sources.html)。
Caltech-101(7)图像数据集有101个类别的图像[25]。我们选取了广泛使用的7个类,得到了1474张[26]图像。这七种类别分别是面孔、摩托车、美钞、加菲猫、停车标志和温莎椅。每幅图像由六个特征描述。
Extended Yale-B是由三种视图描述的人脸图像数据集。综上所述,这个数据集中有38个不同的人脸图像被试。我们选择前10个被试进行多视图聚类,每个被试65张图像(http://cvc.yale.edu/projects/yalefaces/yalefaces.html)。
ALOI包含1000个对象的110,250张图像,每个对象大约有100张图像。该算法提取了10个对象的1079张图像,包括RGB颜色直方图,HSV颜色直方图,颜色相似度,Haralick特征的4个视图。表1给出了上述四个数据集的简要说明。
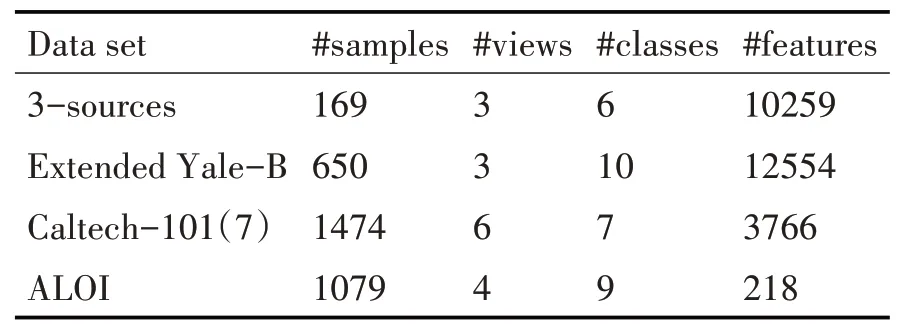
表1 数据的属性
4.2 评价指标
使用三个评价指标[23]来评估我们的结果:聚类精度(ACC),纯度(Purity),标准化互信息(NMI),对于这些广泛使用的指标,值越大表示集群性能越好。这些指标是通过比较每个样本获得的标签与数据集中提供的真实标签来计算的。
4.2.1聚类准确率
ACC是反映聚类的精度,定义为
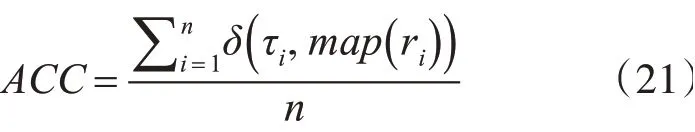
其中n为数据点的个数,τi为第i个样本点真实的类标签,ri为学习到的第i个样本点对应的类标签。δ(x),y定义为一个函数,即当x=y时δ(x,y)=1,否则为0;map(ri)是一个映射函数,它将学习到的标签ri与真实标签τi进行匹配。ACC的取值范围为[0,1],值越靠近1,越好。
4.2.2 纯度
Purity是正确类标签的百分比,定义为
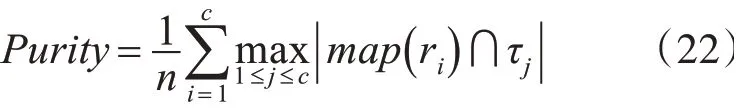
Purity的取值范围为[0,1],值越靠近1,越好。
4.2.3 标准互信息
标准化互信息NMI用于表示τi和ri之间的相似程度,定义为
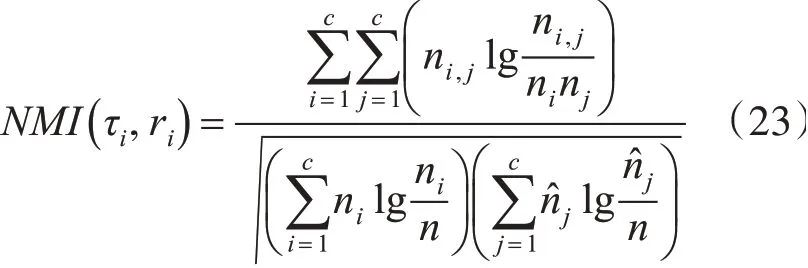
上式中的:ni表示算法中每一类ri(1 ≤i≤c)包含的样本点的个数以及n̂j表示算法中每一类τj(1 ≤j≤c)包含的样本点的个数;ni,j表示学习到的第i个样本点对应的类标签ri和真实的类标签τj的交集中所包含的样本点的个数。NMI的取值范围为[]
0,1,值越靠近1,越好。
4.3 实验设置
4.3.1 对比算法
将本文提出的算法与其它三种聚类算法进行了比较:分别为SWMC[27],AMGL[28],MVGL[29]。比较算法中涉及参数的调整均根据相应文献作者的建议进行设置并试验以显示最优结果,对于所有要求图的相似度矩阵作为输入的算法,我们使用文献[18]中提出的方法来构造每个视图的相似度矩阵,将k固定为10来验证它们的性能,原因使它可以避免不同视图之间的尺度差异,并为每个视图生成归一化相似矩阵。
4.3.2 参数设置
本文算法中的参数λ的取值为{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1}。k取 值 为0~15。我们在图2中描述了不同参数的变化,其中横坐标表示k的取值,纵坐标表示λ的取值,竖坐标表示聚类准确率ACC,具体的设置在四个数据集(a)3-sources、(b)Extended Yale-B、(c)Caltech-101(7)、(d)ALOI上的k和λ的取值分别为(8,0.9),(8,0.2),(10,0.7),(14,0.6)。
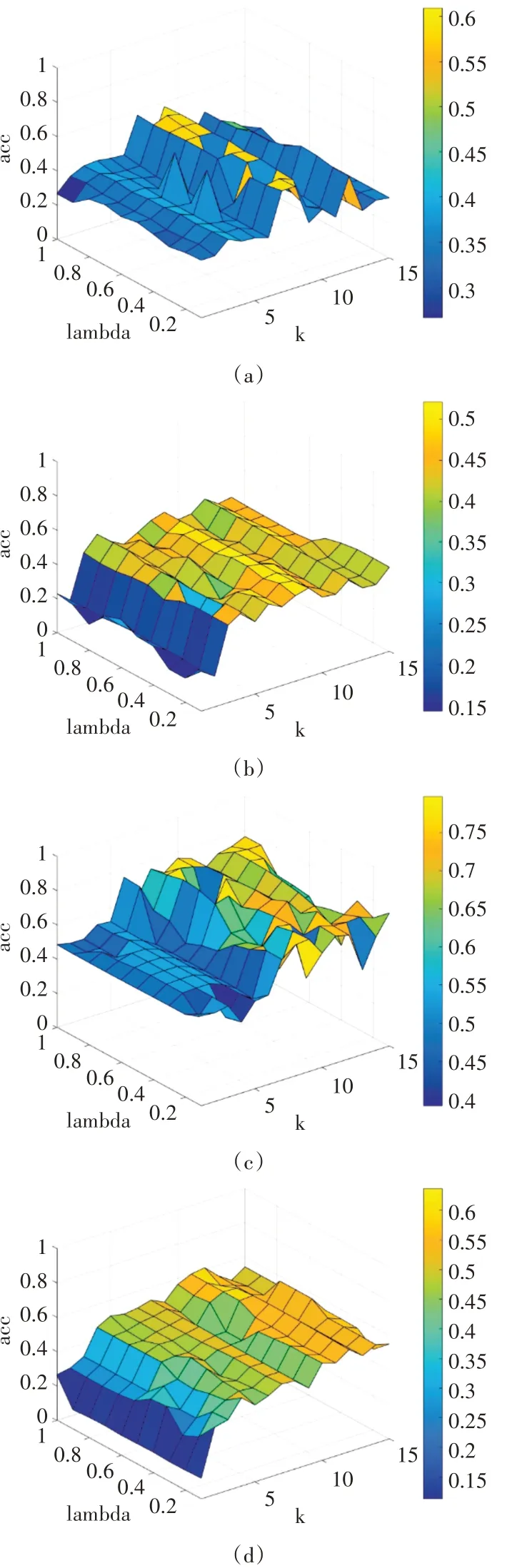
图2 MVSC-L2,1中参数在数据集(a)3-sources、(b)Extended Yale-B、(c)Caltech-101(7)、(d)ALOI上的变化
4.4 实验结果
从表2、表3和表4显示的结果中可以得到,在ACC,Purity和NMI三个评价指标下,首先在数据集3-sources上,我们所提的算法,相比次优的分别提高23.84%、20%、19.6%;在数据集Extended Yale-B上,我们所提的算法,相比次优的分别提高6.77%、7.08%、6.56%;在数据集Caltech-101(7)上,我们所提的算法,相比次优的分别提高0.13%、0.07%、7.43%;在数据集ALOI上,我们所提的算法,相比次优的分别提高8.89%、0.88%、0.52%。综上,我们的算法MVSC-L2,1的聚类性能明显高于对比算法,具有良好的聚类效果。
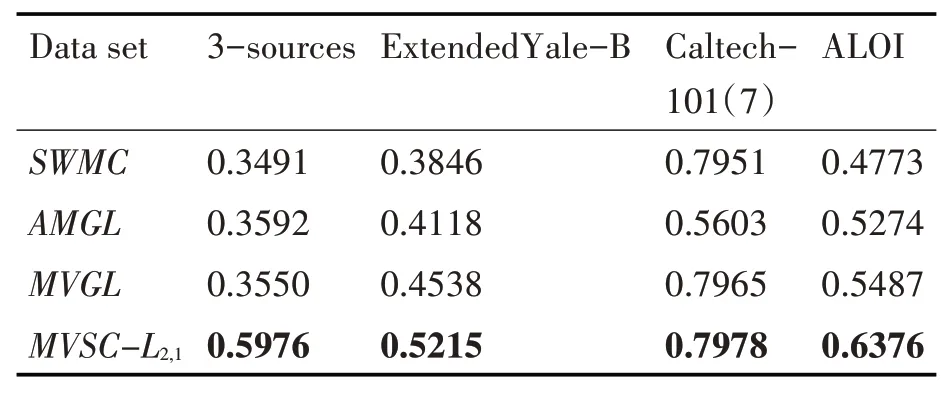
表2 不同算法在各数据集下的ACC比较
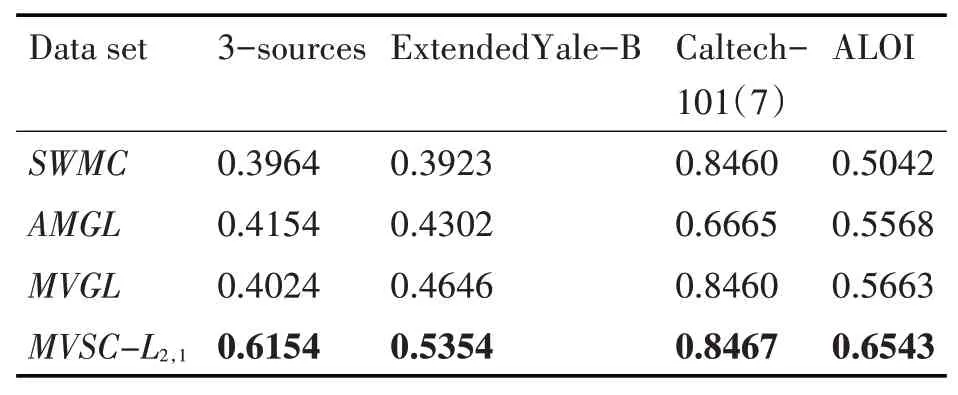
表3 不同算法在各数据集下的Purity比较
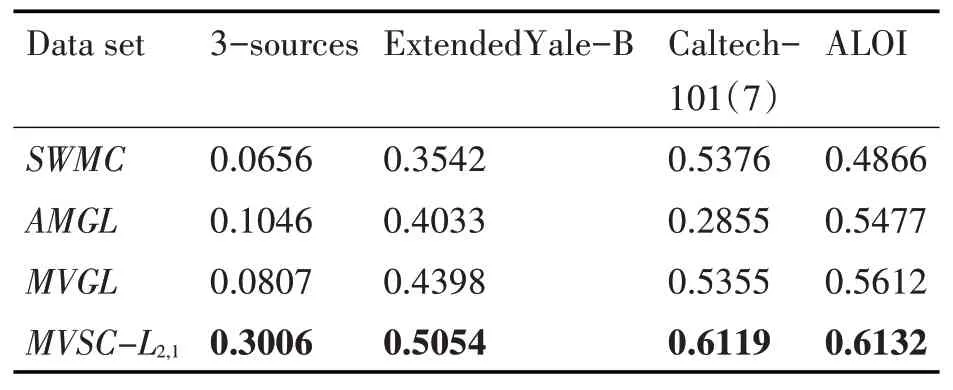
表4 不同算法在各数据集下的NMI比较
5 结语
本文提出了一种新的多视图聚类算法MVSC-L2,1,该算法在构造相似矩阵时,采用将各个视图的信息相加融合的方式,比单视图算法更优,然后同时进行相似矩阵和谱聚类过程,更新迭代优化S和F,最后对F进行聚类。在多个数据集上的实验结果表明,该算法可以产生较好的聚类结果。但是由于参数λ是人为选取的,使得该算法有一定的局限性。如何自动确定参数,是下一步的研究方向。
